物联网智能感知节点基于π网软硬件划分模型研究

刘晓霞，周绍军

(四川水利职业技术学院信息工程系，四川 崇州 611231)

随着物联网的不断发展，智能感知已广泛的应用且为物联网感知领域的重要基础设施.智能感知节点将感知信息采集、实时信息处理和实时通信于一体，如智能交通领域的车联网，若在行进路上发生故障或事故，则智能感知系统将位置、环境状况等信息进行实时感知、处理，并将处理后的信息进行实时传输，以便得到快速处理.智能感知节点具有较高的性能，如全新的、覆盖面广和实时性强等特点，又如互通信、互操作能力等；而且，智能感知节点在功耗、体积、处理器速度等方面存在约束；因此，急切需要对其软硬件划分进行研究.

就软硬件划分算法而言，国内外研究者对其进行了诸多研究.文献[1]提出了基于可满足性理论(Satisfiability Modulo Theories，SMT)的软硬件划分算法，并进行了实验验证.文献[2]利用最新的不确定性理论对线性不确定分布和正态不确定分布，提出一种用于硬件/软件资源共享的参数增强系统划分不确定性模型，并对模型进行了分析与验证.文献[3]在不牺牲系统质量的情况下，提出图归约技术进行软硬件划分，以减少进行系统设计时的软硬件划分的设计空间.文献[4]提出一种将流式细胞粒度的粒子群优化算法、模糊C均值算法和粒子群优化算法相结合的二进制多核软硬件划分算法.文献[5]提出了两种软硬件划分算法，即启发式的扩展0-1背包算法和基于禁忌的启发式算法.文献[6]利用生物行为学理论，提出一种基于从众和声粒子群算法的冰箱软硬件划分方法.文献[7]提出一种将遗传算法与蚂蚁算法进行动态融合的软硬件划分算法.文献[8]对可重构的FPGA利用混合式两阶段的动态重构建立软硬件划分算法.文献[9]将软硬件划分问题看作带有动态通信代价的变异0-1背包问题，提出一种基于迭代排序思想的NodeR-ank算法.这些研究，针对一般嵌入式系统而进行软硬件划分研究，提出了相应的算法；但未针对物联网智能感知节点的具体特点，进行具有针对性的软硬件划分研究；因此，本文针对物联网智能感知节点的特殊性，对其进行软硬件划分研究，是十分必要的.

π网是一种基于Petri网和π演算的高级建模方法，主要用于描述和刻画并发系统，并能发挥Petri网的图形和数学优点，又能充分体现和应用π演算的代数特性，非常适合描述软硬件设计过程中的并发行为[10].因此，在此利用π网理论，建立物联网智能感知节点在硬件面积、成本、实时性和可靠性等约束下的软硬件划分算法，并对算法进行分析和实验验证.

1 智能节点模型

物联网三层体系结构中，最底层为感知层，由诸多感知设备构成，如RFID设备、视频采集终端、传感器感知终端和条码终端等等.而这些感知设备大多是智能设备，能够完成对物质世界的感知、处理和传输，故其功能需求可用任务流程图来描述[11].

在智能节点任务流程图中，一个顶点vi表示一个功能IPi核，有向边eij表示IPi核和核IPj间的依附关系；有向边上的数字ωij表示顶点vi到顶点vj的约束条件；其中i，j＝1，2，…，n.一个任务流程图中有且仅有一个顶点的入度为0、有且仅有一个顶点的出度为0，将这两个顶点分别称为起始顶点和终止顶点；同样，在智能节点任务图中，存在一条由起始顶点到终止顶点的关键路径，且关键路径由图中的若干相互依附的顶点组成.如图1所示，其中v1表示智能节点的某种功能的软硬件划分开始，vn表示得到该功能的软硬件划分之最优结果.

图1 智能节点功能IP核任务图Fig.1 Intelligent node function IP kernel task diagram

物联网智能感知节点存在很多约束，比如在硬件面积/体积、能耗、可靠性和实时性等.同时，智能节点还具有相应的性能指标要求.假定智能节点的性能指标PI1不超过Bq1、性能PI2不能超过Bq2……，性能指标PIn不能超过Bqn，则性能指标PIi(i＝1，2，…，n)的实现存在两种方法，即硬件实现和软件实现，且每种实现具有不同的性能指标数据.设Ci为n元组，即Ci＝(PIi1，PIi2，…，PIin)，则以C描述智能节点设计时的第i个IP核，其中PIi1，PIi2，…，PIin为与该 IP核对应的需重点考虑和评价的性能参数[12].

物联网智能感知节点在设计时，需要重点考虑节点能耗和响应时间.因智能感知节点大多为电池供电，存储的能量是及其有限的.智能感知节点的第i个IP核的能耗主要由空闲能耗和运行能耗构成，即:

其中:Eidle，Erun分别表示空闲能耗和运行能耗；Eidle(i)表示第i个IP核空闲能耗；Erun(i，task)表示第i个IP核运行时能耗；i为1，2，…，n中取值.故得到智能感知节点的总能耗为:

智能感知节点的响应时间，特别是对实时感知而言，就显得尤为重要.节点的响应时间由感知时间、处理时间和通信时间构成，故可表示为:

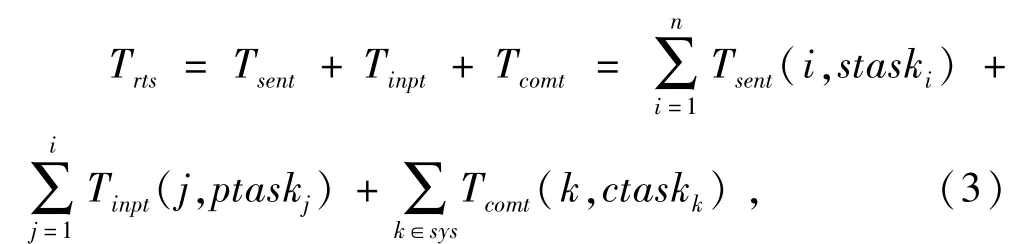
其中:i，j，k均为 1，2，…，n中取值；staski)表示多种感知任务的响应时间进行累加；(j，ptaskj)表示多种感知信息进行处理所需要的时间的累加；Ecomt(k，taskk)表示整个智能感知节点的通信所需时间的累加.

假定物联网智能感知节点的主要性能指标及其约束为:能耗 ≤E；成本 ≤Cost；面积 ≤Ma；重量 ≤W；可靠性≤R；体积≤V；响应时间≤Rt；则可对第i个IP核而言，就有:

其中:i表示 IP 核，且 1 ≤i≤n；k0，k1，k2，k3，k4，k5，k6为确定的常数，为第i个IP核的备选项的数目.

定义1假定物联网智能感知节点由若干IP核组成，即:

则每个IP核均存在一组供选的构件集合，即:

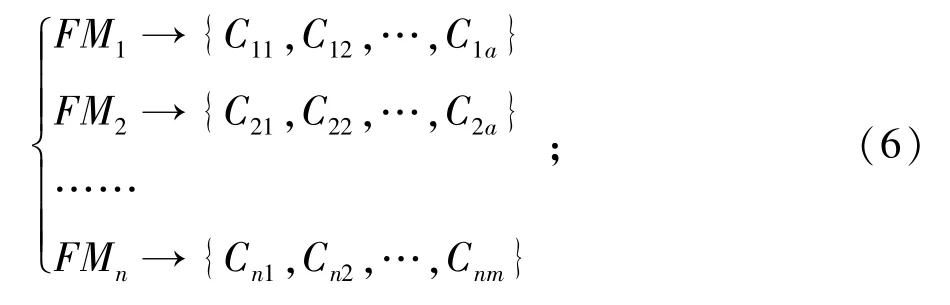
其中:C为服从式(1)；a，b，…，m是常数，分别表示FM1，FM2，…，FMn所对应的备选IP核的数目.

由此，物联网智能感知节点的软硬件划分问题就转化为求CMisn的一个组合 (C1i，C2j，…，Cnt) ，其中1≤i≤k0，1 ≤j≤k1，…，1 ≤t≤k6，且满足:

故得到物联网智能感知节点结构模型如图2所示.

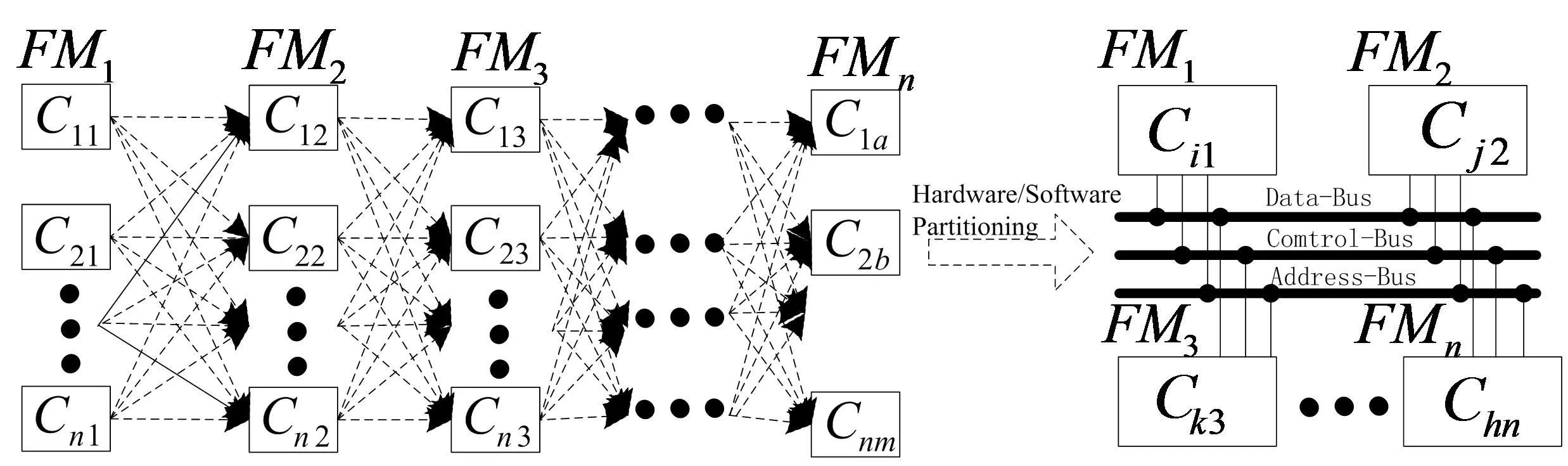
图2 物联网智能感知节点结构模型Fig.2 Intelligent perceptive node structure model for Internet of things

2 软硬件划分模型

依据π网理论和智能感知节点模型，可定义物联网智能感知节点的软硬件划分模型HSPM(Hardware/Software Partitioning Model，HSPM)[11].

定义2 物联网智能感知节点的软硬件划分模型HSPM 为一个 π网NHSPM，即NHSPM＝(EHW，ESW，EF；Eτ)，其中:EHW为设计中的硬件IP核实现的功能集合，是网NHSPM的库所集；ESW为系统设计中软件IP核实现的功能集合，是网NHSPM的变迁集，使得EHW∩ESW＝φ；EF⊆(EHW×ESW)∪(ESW×EHW)是网NHSPM的有向弧集，表示网NHSPM的对应关系；Eτ是定义在EHW∪ESW∪EF上的一个属性函数，表示物联网智能感知节点设计中的各种约束评价因子所构成的函数关系.

[11]，可得到模型NHSPM的软硬件划分算法步骤为:

第一步:输入、输出和约束条件设置.输入设置:物联网智能感知节点的任务图及网NHSPM的初始条件、可选IP核库所、约束条件；输出设置:符合约束条件的划分集合，并进行最优化处理；约束条件设置:按照式(4)设定每个可选IP核的约束值，得到每个IP核的约束条件矩阵；

第二步:生成初始网.依据输入生成初始π网，得到初始的网；

第三步:初始π网进行演算.依据π网理论，在初始输入设置下进行初始π网演算；

第四步:子网划分.依据规则1和规则2，对初始π网进行变迁使能和激发，同时进行输入库所的标识变迁使能与激发，得到中间π网N′HSPM；依据约束条件进行库所、变迁的删减，得到最小网；在网N″HSPM中，计算变迁的最小时间及其对应的子网，直到得到网中无同时被两个变迁同时覆盖的变迁，否则继续进行子网划分；

第五步:得到演化与划分后的π网，即NHSPM模型.经过第三、四步，在约束条件下，对得到的网进行性能评估，若符合所输入的约束条件，则得到模型NHSPM，否则返回第三步；

第六步:对模型进行效用评估.对得到的模型进行效用度计算，并将其与给定的约束条件中的效用度值进行比较，若其值小于约束中的效用度值，则返回第一步；

第七步:输出划分结果.符合约束条件的划分，输出划分结果，启用最优化处理；

第八步:得到最优的划分结果.从所有符合约束条件的划分输出中，采用多目标最优化处理方法，得到最优的结果，并以此作为物联网智能感知节点的软硬件划分的最后结果输出；否则返回到第一步.

因此，物联网智能感知节点软硬件划分模型NHSPM可表示为如图3所示.图3中，左边为模型NHSPM的库所、变迁在约束条件下，进行软硬件划分时的过程；右边为模型NHSPM进行划分之后，得到选中的可选IP核构成的智能感知节点模型.图3中，Datai(i＝1，2，…)为第i个库所的约束条件集合，其定义服从公式(4).

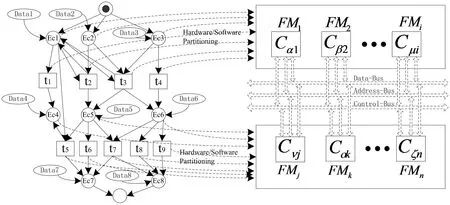
图3 π网的迁移变迁与划分结果的映射关系Fig.3 Mapping relationship between the migration and transition of the pion network and the result of the partition

3 模型动态演进分析

在得到物联网智能感知节点π网软硬件划分模型后，利用π网理论，对模型完成动态化的演化分析.

模型NHSPM动态化的演化，在此仅仅探究候选IP核的创建、删除和更新等情况.

候选库所有新的库所加入时，该新的库所必须先进行库所注册，使其存储并作为库所候选库的一个候选库所.新库所建立进程NewPlace可描述为:

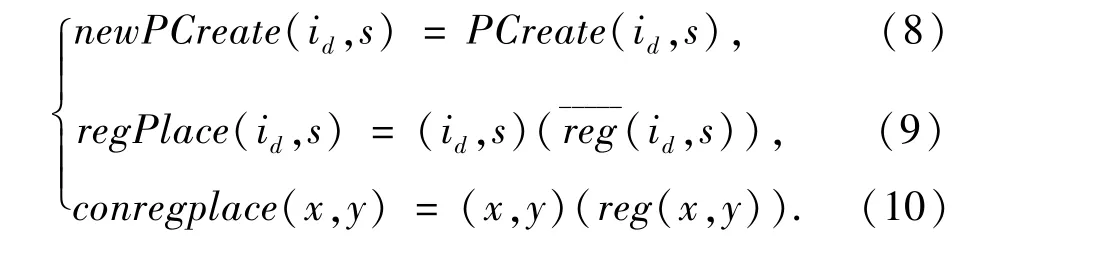
其中:式(8)表示新库所创建；式(9)表示新库所注册；式(10)表示新库所加入候选库中.

新库所加入到候选库后，需要参与模型的各种变迁.新库所的变迁NewPlaceP进程可描述为:

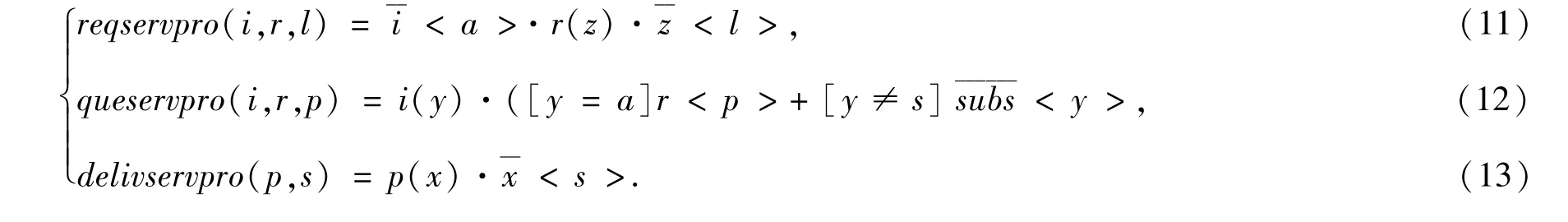
其中式(11)为请求服务的进程；式(12)为连接件中相应的服务查询进程；式(13)服务提供进程.

若新库所不完备时，利用π网的弱时间等价互模拟关系，则将(12)改写为:

其中:Rf是在定义3的八元组上对时间的抽象与进程Qf的弱时间等价.

因此，模型NHSPM增加新的库所时，能够在库所库中实现动态交互.

若候选库所集合中的库所进行变化或升级，则需要对原库所进行更新.库所更新方式主要有保持语义更新和扩展性更新[13].

规则 1 设候选 IP 核Cp，0的接口为P，组件Cp，1的接口Q，若P≈Q成立，并∃α和M，有α·P＋M≈α·Q＋M成立，则称Cp，1可使Cp，0进行保持语义更新.

规则 2 设候选 IP 核Cp，0的接口为P，Cp，1的接口为Q，若P和Q使得:

(1)fn(P)⊆fn(Q)，即P的自由名字是Q自由名字的子集；

同时成立，则进程Q对P进行了扩展性更新，标记为P≺Q；故Cp，1对Cp，0进行了扩展性更新.

由此，模型NHSPM可进行动态化更新，进而可实现动态化的演化.

4 实验与仿真

物联网智能感知节点的硬件划分目标是搜索功能分配到软硬件模块，使得其设计不仅满足能耗有限性的需求，还要满足执行时间、可靠性、可用性、面积、体积和重量等的限制，并在这些约束下使其指标达到最优.因此，采用先进Pareto优化算法(Advanced Pareto Optimization Algorithm，APOA)实现对模型NHSPM的优化.

依据参考文献[14]提出的方法，对模型NHSPM进行代与代之间维持由潜在解组成的种群来实现全局搜索，得到多目标优化的Pareto最优解集，即为模型NHSPM的最优解.首先，对所有候选库所进行Pareto排序，并在能耗、可靠性、可用性、执行时间和成本等约束下，对库所进行调度，估算成本和功耗等且用Pareto排序；然后计算个体的适应度值，进行选择与交叉，同时进行变异运算；再进行父代与子代的混合，得到新的种群，依据等级和适应度值取前50%作为下一代种群，而重新启动优化；最后输出当前选中的种群，即为Pareto最优解.其优化流程如图4所示.

图4 APOA优化流程Fig.4 APOA Optimization process

对先进 Pareto优化算法(APOA)、遗传算法(GA)、蚂蚁优化算法和禁忌搜索算法(TS)作了对比，每个算法的输入都是相同属性的π网[15].并在实验过程中，每种算法使用相同的可知参数，亦确保不同算法具有可比特性.通过实验，得到如图5所示的实验结果.

物联网智能感知节点的实例，采用多参数智能感知某环境的温度和湿度，要求实现无线数据远程传输；由此得到该智能感知节点功能模块可分为温度模块、适度模块、无线通信模块、处理器模块和电源模块等，而每个模块对应诸多候选选项，如温度模块而言，仅硬件接触测温和非接触测温两大类型，其中接触测温可采用集成温度传感器、Pt100、热电偶、热电阻和半导体传感器，非接触又可采用红外测温、比色测温和超声测温等.物联网智能感知节点的各种约束条件的值，可使用一维数组描述为 Cz＝(16650mah，1500rmb， 3ms， 0.9999， 0.9487， 2000mm2， 200g，30000mm3)，分别表示节点在能耗、成本、响应时间、可靠性、可用性、面积、重量和体积等约束.通过实验得到如表1所示数据.

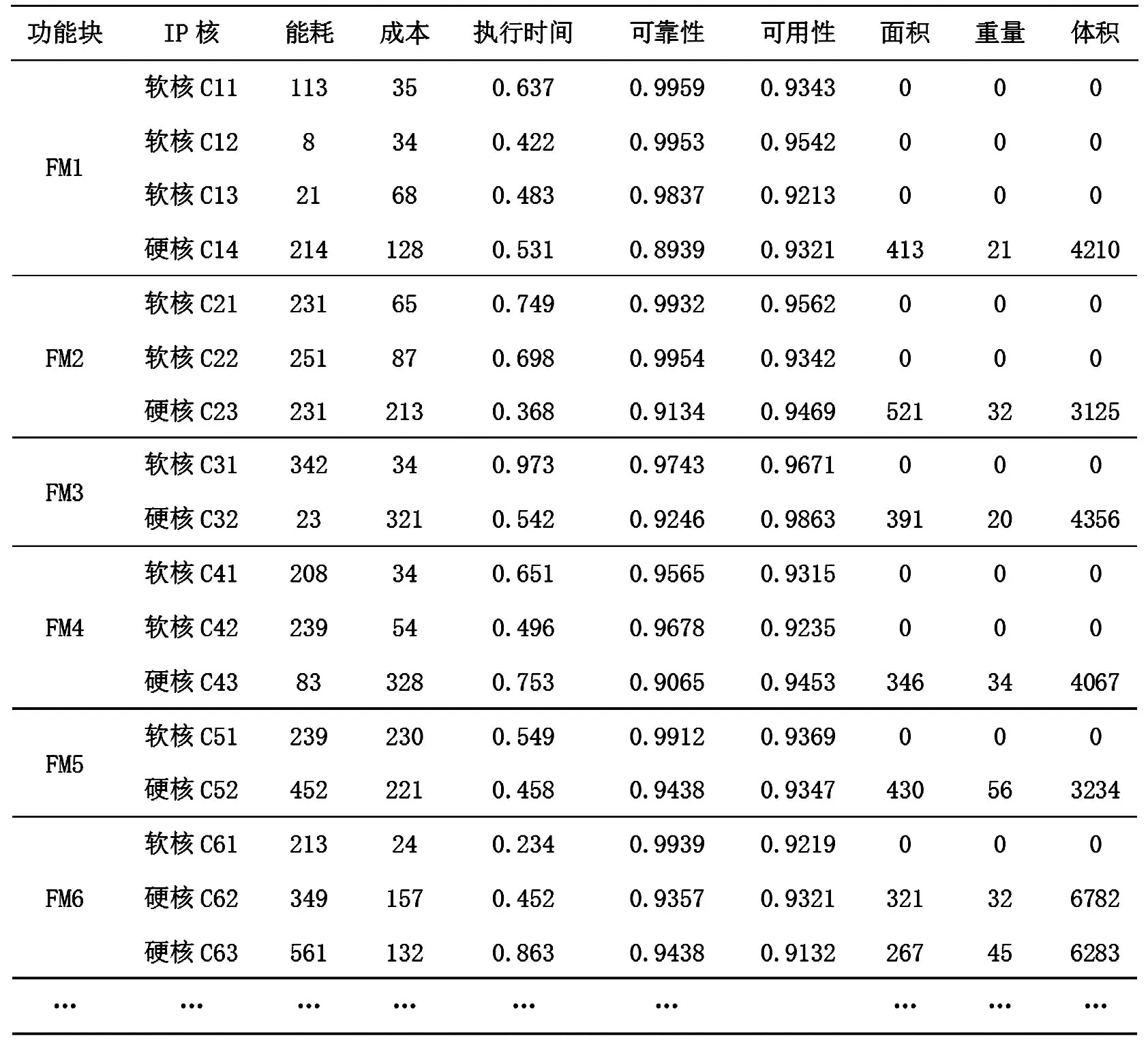
表1 候选IP核库所及其约束表Table 1 Candidate IP core library and its constraint table

利用模型NHSPM得到的该智能节点的软硬件划分，与使用遗传算法和蚂蚁算法进行的软硬件划分，在划分执行时间上进行对比实验，得到如图6所示对比图.

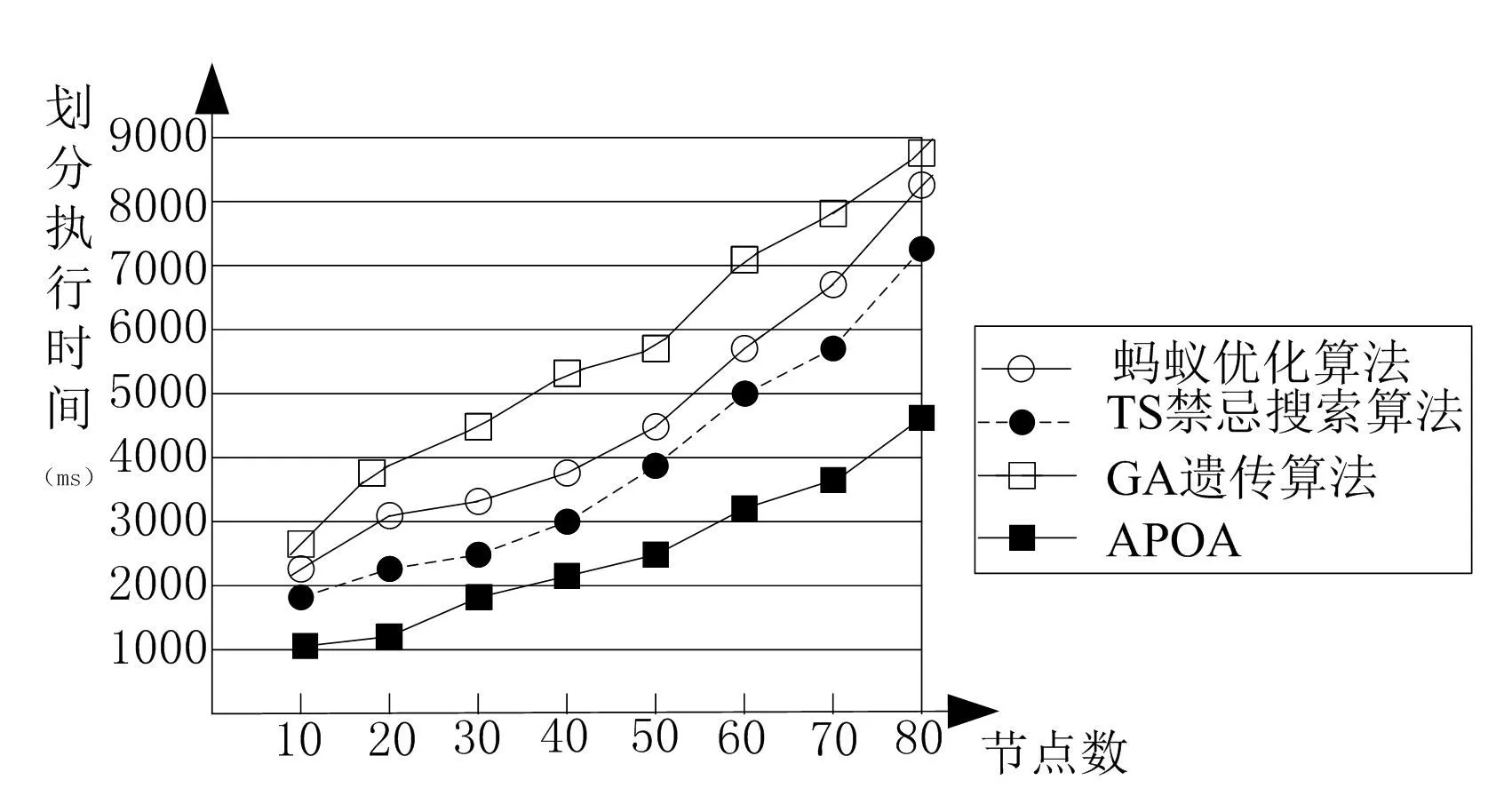
图6 不同算法划分运行时间对比曲线Fig.6 Different algorithms for dividing running time contrast curves

在多参数智能感知情况下，本实验在一定的约束条件下优化其软硬件划分.通过实验与仿真，模型NHSPM在划分运行时间上和适应度方面，较基于蚂蚁算法、TS禁忌搜索算法和GA遗传算法在多参数智能感知下进行软硬件划分，性能具有一定的优越性.

5 结论

物联网智能感知节点的软硬件存在划分问题，其划分方法直接影响性能、使用寿命等.本文在对物联网智能感知节点进行带约束定义，得到了智能感知节点的约束模型；然后利用π网理论，建立了基于π网的物联网智能感知节点软硬件划分模型，并对模型进行了演化分析；再后，利用先进Pareto优化算法对划分模型进行了优化，同时与TS禁忌搜索算法和GA遗传算法等进行了对比实验.通过分析与实验仿真，基于π网的物联网智能感知节点软硬件划分模型，在适应度方面优于TS禁忌搜索算法和GA遗传算法.因此，本文建立的模型，具有一定的先进性和实用性.

参考文献

[1]TRINDADE A B，CORDEIRO L C.Applying SMT-based verification to hardware/software partitioning in embedded systems[J].Design Automation for Embedded Systems，2016，20(1):1-19.

[2]WANG RUI，HUNG W N N，YANG GUOWU，et al.Uncertainty model for configurable hardware/Software and resource partitioning[J].IEEE Transactions on Computers，2016，65(10):3217-3223.

[3]JIANG GUIYUAN，WU JIGANG，LAM S K，et al.Algorithmic aspects of graph reduction for hardware/software partitioning[J].The Journal of Supercomputing，2015，71(6):2251-2274.

[4]MHADHBI I，OTHMAN S B，SAOUD S B.An Efficient Technique for Hardware/Software Partitioning Process in Codesign[J].Scientific Programming，2016(6):1-11.

[5]WU JIGANG，WANG PU，LAM S K，et al.Efficient heuristic and tabu search for hardware/software partitioning[J].The Journal of Supercomputing，2013，66(1):118-134.

[6]鄢小虎，何发智，陈壹林.一种基于从众和声粒子群算法的并行软硬件划分方法[J].中国科学:信息科学，2016，46(9):1321-1338.

[7]熊志辉，李思昆，陈吉华.遗传算法与蚂蚁算法动态融合的软硬件划分[J].软件学报，2005，16(4):503-512.

[8]马昱春，张超，WAYNE.基于混合式两阶段的动态部分重构FPGA软硬件划分算法[J].清华大学学报(自然科学版)，2016(3):246-252.

[9]陈志，武继刚，宋国治，等，NodeRank:一种高效软硬件划分算法[J].计算机学报，2013，36(10):2033-2040.

[10]曹木亮，吴智铭，杨根科.一类新型的模块化高级Petri网－π网[J].上海交通大学学报，2004，38(1):52-58.

[11]陈玮，顾思思.基于组合算法的嵌入式系统软硬件划分方法[J].计算机应用与软件，2015(10):240-243.

[12]SHAHROUZI S N，PERERA D G.Dynamic partial reconfigurable hardware architecture for principal component analysis on mobile and embedded devices[J].Eurasip Journal on Embedded Systems，2017(1):25-43.

[13]何海洋，李强，余祥，等.基于高阶π演算的构件演化行为研究[J].计算机科学，2017，44(3):202-208.

[14]朱杰兵，李聪，曾平.基于多目标模糊优化算法的边坡变形组合预测模型[J].固体力学学报，2014(s1):276-280.

[15]潘颖，阮文惠.基于改进蚁群算法的嵌入式系统软硬件划分[J].现代电子技术，2017，40(3):164-166.