关于对称共轭点的亚纯双向单叶倒星象函数类的系数估计

马丽娜，李书海，张海燕

(赤峰学院数学与统计学院，内蒙古 赤峰 024000)

1 引言

令A表示单位圆盘U＝内解析且具有如下形式的函数类.

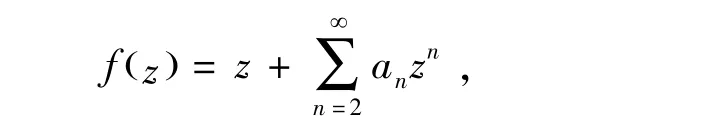
设Σ表示去心单位圆盘U∗U＼{0}内解析且具有如下形式的亚单纯叶函数类

对于每一个函数f(z)∈Σ，具有逆函数f－1，定义为

及

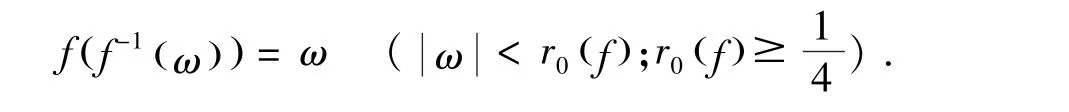
对于具有(1)形式的函数f(z)的逆函数f－1具有如下形式，

若函数f和f－1都在U∗内单叶，则称函数f(z)∈Σ在U∗内亚纯双向单叶.近来，许多学者对亚纯双向单叶函数进行了研究，详见文献[1-7].

令P表示在U内解析且具有如下形式

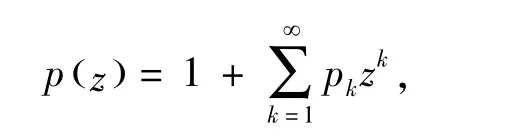
的函数p(z)的全体，且Rep(z)>0.

设函数u(z)和v(z)在A中解析，若存在一个Schwarz函数ϖ，在U内满足ϖ( 0)＝0和使得u(z)＝v( ϖ(z))(z∈U)，则称函数u(z)从属于v(z)，记作u(z)≺v(z).另外，若v在U内单叶，则u(z)≺v(z)等价于

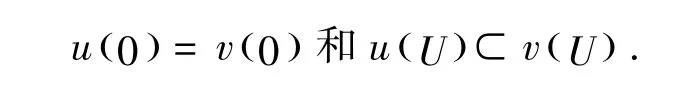
函数f(z)∈A属于函数类S∗(φ)，如果满足如下条件

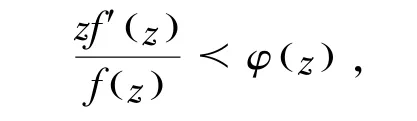
其中φ(z)∈P.函数类S∗(φ)和相应的凸函数类K(φ)由Ma和Minda定义[8].

1959年，Sakaguchi[9]引入关于对称点的星象函数类当且仅当

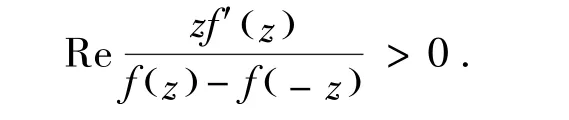
1987年，El-Ashwa和Thomas[10]引入并研究了关于共轭点的星象函数类及关于对称共轭点的星象函数类，分别满足如下条件

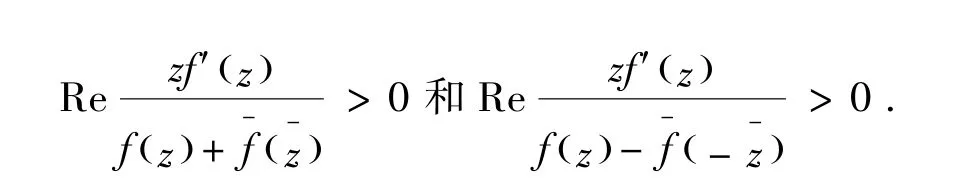
本文将研究一类具有对称共轭点的亚纯双向单叶倒星象函数类如下，

定义1.1函数f(z)∈Σ属于关于对称共轭点的亚纯双向单叶倒星象函数类ΣSsc(φ)当且仅当

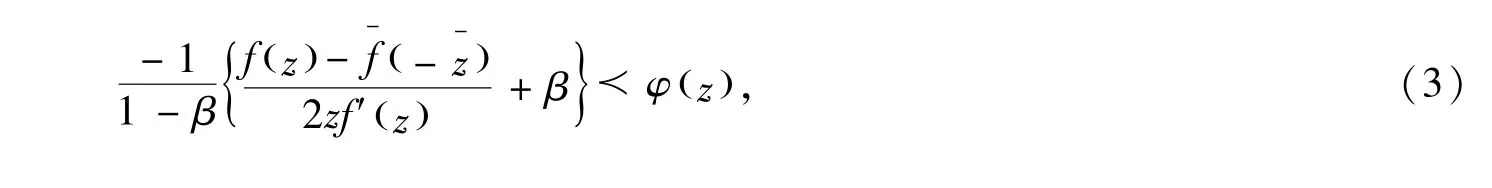
及

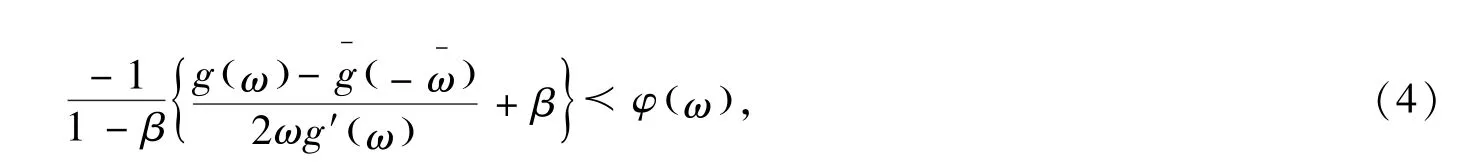
其中g(ω)＝f－1(ω)，φ(z)＝1＋B1z＋B2z2＋…，B1>0，β<1.

2 积分表达式

首先，定义的函数类的积分表达式.所得结论推广了亚纯p叶函数类的一般已得到的积分表达式[11－13].

定理2.1若f(z)∈ ΣSsc(φ)，则

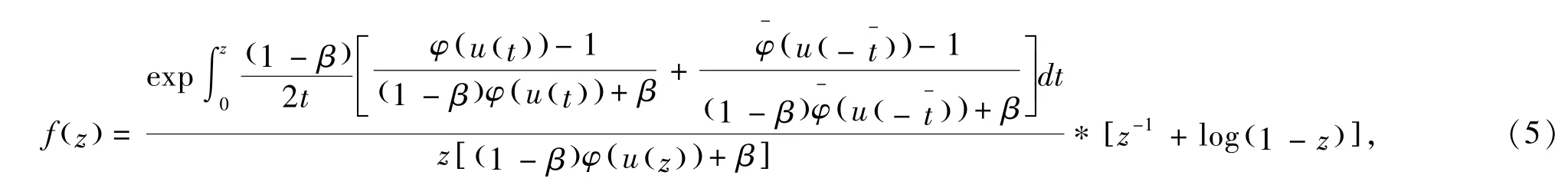
其中u(z)在U内解析且u(0)＝0及

证明:因为f(z)∈ ΣSsc(φ)，则

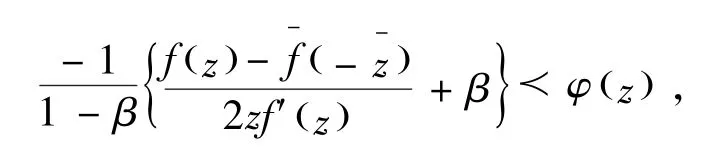
及

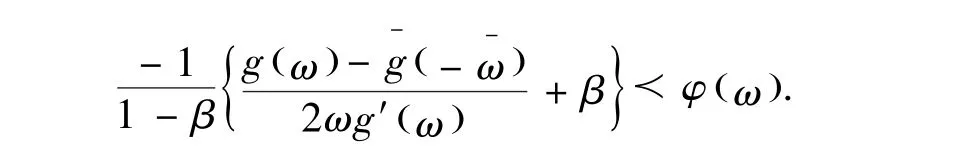
根据从属关系定义，存在解析函数u，v:U→U满足u(0)＝v(0)＝0，，使得

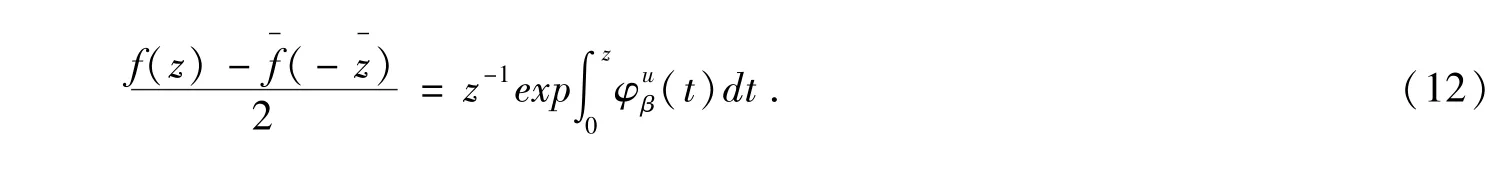
根据(8)和(12)式，有

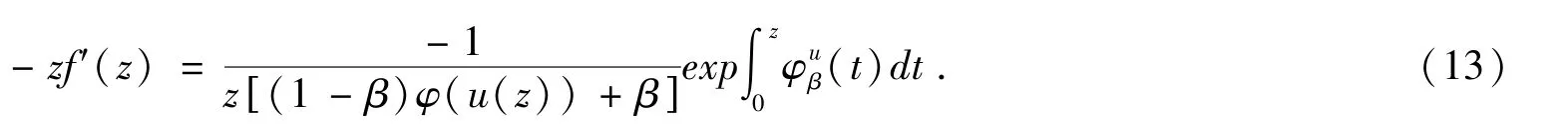
根据Hadamard积(卷积)的性质，有

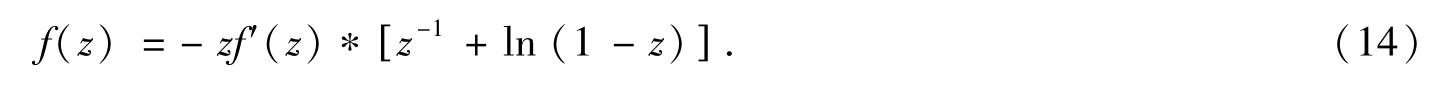
因此，利用式(11)，(13)及(14)，有

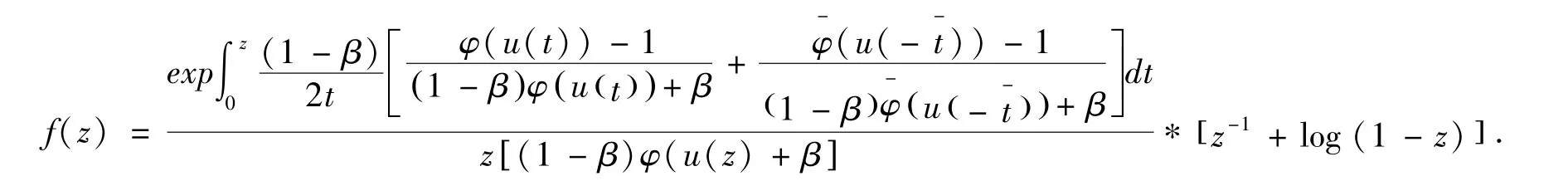
从而定理2.1得证.

3 系数估计

引理3.1[14]如果p(z)＝

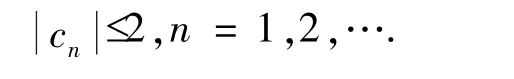
上面的不等式估计是精确的.当函数p(z)时，不等式的等号成立.

引理3.2[15-16]如果p(z)＝则存在复数x，y，且使得

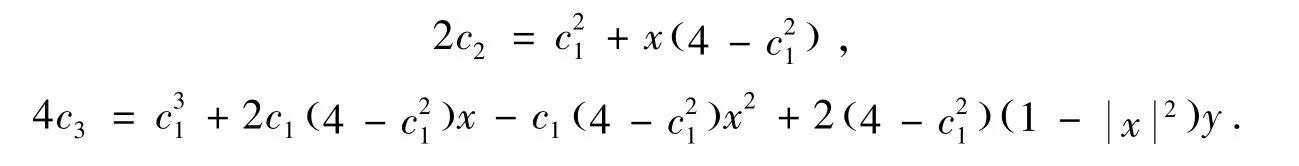
定理3.1函数f(z)具有(1)式形式，若f(z)∈ΣSsc(φ)，则有如下系数估计

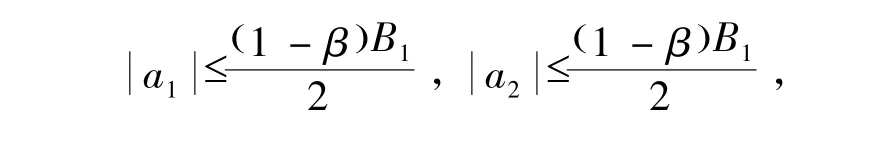
及

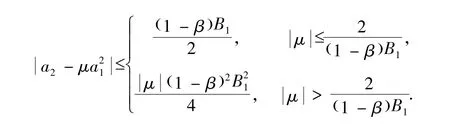
上面估计是精确的.

证明:因为f(z)∈ΣSsc(φ)，根据定义1.1及根据从属关系定义，存在解析函数u，v:U→U满足u(0)＝使得

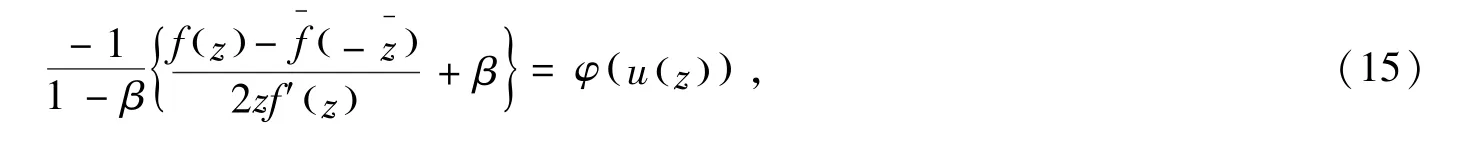
及

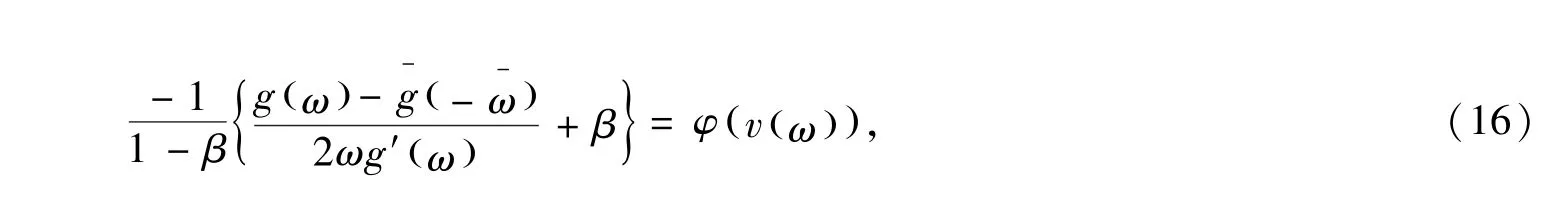
令

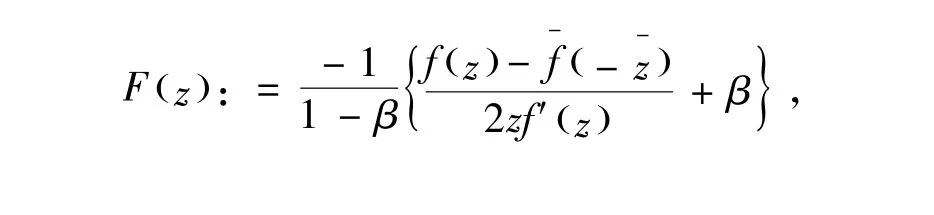
及

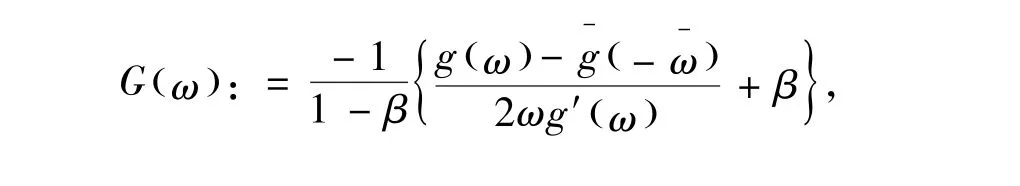
从而有

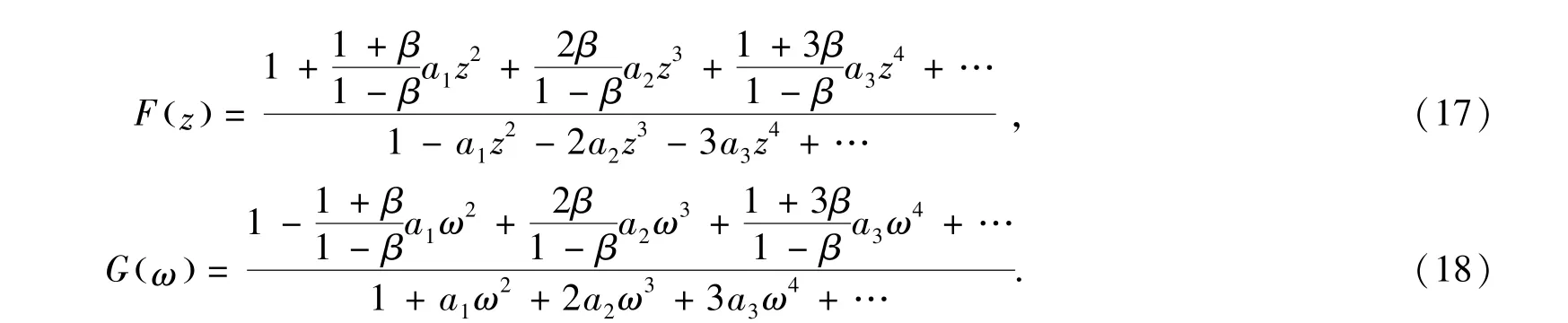
分别定义函数p(z)和q(ω)如下

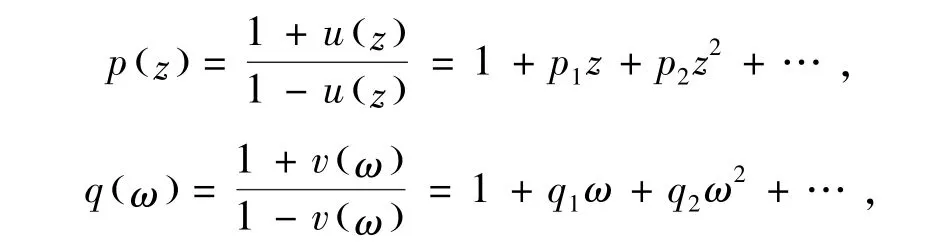
即，

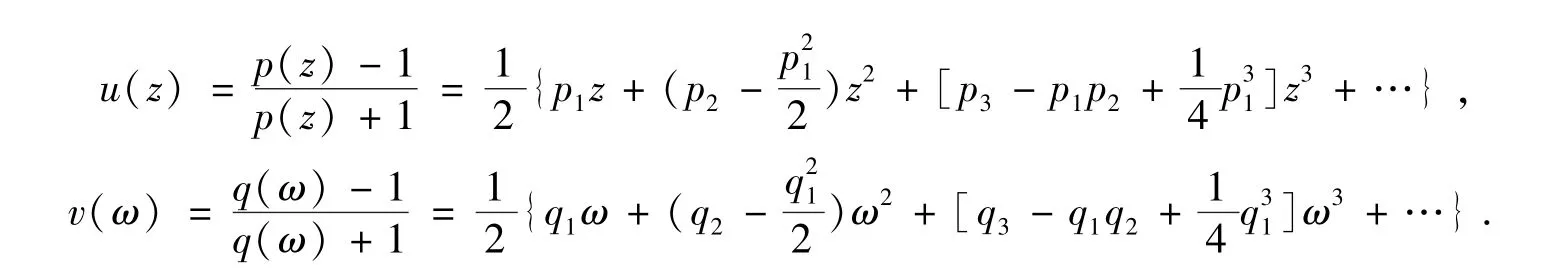
显然p，q∈P.从而，有

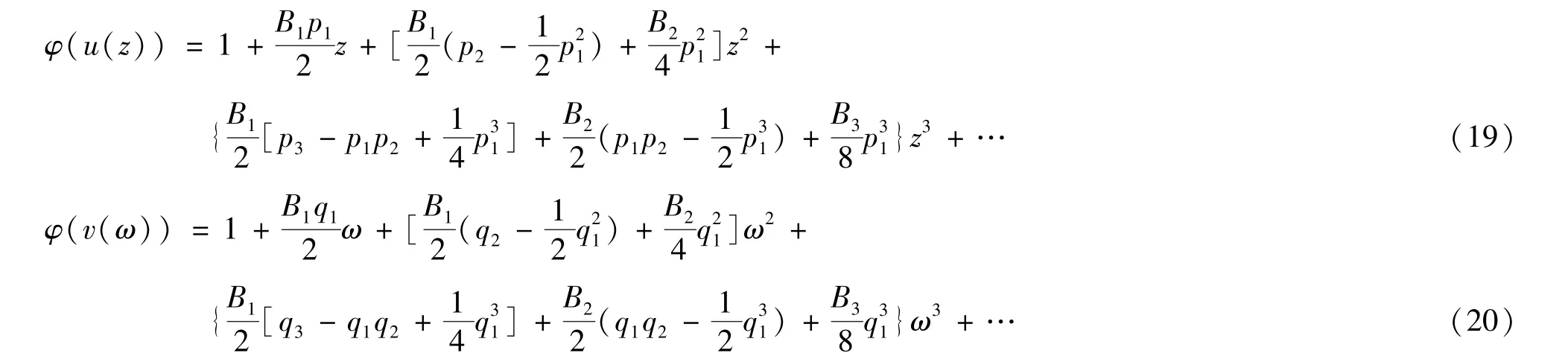
根据式(15)-(20)，得p1＝q1＝0，及

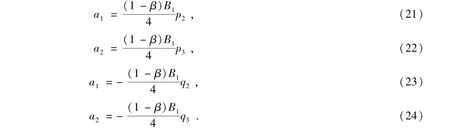
因此，有p2＝－q2，p3＝－q3.

利用引理3.1，得

另一方面，

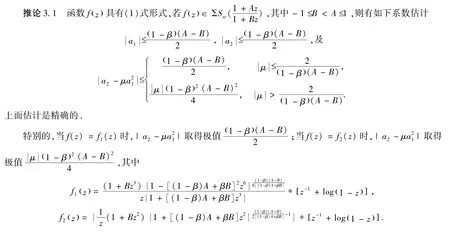
[1]BULUT S.Coefficient estimates for new subclasses of meromorphic bi-univalent functions[J].International Scholarly Research Notices，2014，2014:1-5.

[2]SCHIFFER M.Sur un probleme d'extremum de la representation conforme[J].Bulletin de la Societe Mathematique de France，1938，66:48-55.

[3]DUREN P L.Coefficients of meromorphic schlicht functions[J].Proceedings of the American Mathematical Society，1971，28(1):169-172.

[4]HAMIDI S G，JANANI T，MURUGUSUNDARAMOORTHY G，et al.Coefficient estimates for certain classes of meromorphic bi-univalent functions[J].Comptes Rendus Mathematique，2014，352(4):277-282.

[5]BULUT S，MAGESH N，BALAJI V K.Faber polynomial coefficient estimates for certain subclasses of meromorphic bi-univalent functions[J].Comptes Rendus Mathematique，2015，353(2):113-116.

[6]XIAO H G，XU Q H.Coefficient estimates for three generalized classes of meromorphic and bi-univalent functions[J].Filomat，2015，29(7):1601-1612.

[7]AZIZ F S，JUMA R S.Estimating coefficients for subclasses of meromorphic bi-univalent functions associated with linear operator[J].TWMS Journal of Applied and Engineering Mathematics，2014，4(1):39-44.

[8]MA W，MINDA D.A unified treatment of some special classes of univalent functions[M]//Proceedings of the Conference on Complex Analysis，Internat Press，1994:157-169.

[9]SAKAGUCHI K.On a certain univalent mapping[J].Journal of the Mathematical Society of Japan，1959，11(1):72-75.

[10]El ASHWAH R M，THOMAS D K.Some subclasses of closed-to-convex functions[J].J Ramanujan Math Soc，1987，2:86.

[11]WANG ZHI GANG，JIANG YUE PING，SRIVASTAVA H M.Some subclasses of meromorphically multivalent functions associated with the generalized hypergeometric function[J].Computers and Mathematics with Applications，2009，57:571-586.

[12]SHI LEI，WANG ZHI GANG，ZENG MING HUA.Some subclasses of multivalent spirallike meromorphic functions[J].Journal of Inequalities and Applications，2013，2013:336.

[13]彭娟，刘文娟，杨清.与函数类(α；a，c；h) 有关的积分表示和卷积性质[J].淮阴师范学院学报(自然科学版)，2012，01:22-25.

[14]DUREN P L.Univalent Functions[M].Grundlehren der Mathematischen Wissenschaften，Band 259，New York，Berlin，Heidelberg and Tokyo:Springer-Verlag，1983.

[15]LIBERA R J，ZLOTKIEWICZ E J.Early coefficients of the inverse of a regular convex function[J].Proc Amer Math Soc，1982，85(2):225-230.

[16]LIBERA R J，ZLOTKIEWICZ E J.Coefficient bounds for the inverse of a function with derivatives in P[J].Proc Amer Math Soc，1983，87(2):251-257.