基于最大熵模型的大连北站客运枢纽换乘客流预测

徐鹏，左忠义,白妍

(1.大连交通大学 交通运输工程学院，辽宁 大连 116028； 2.伊利诺伊大学厄巴纳香槟分校 土木与环境工程学院，美国 伊利诺伊州 61874)

0 引言

应用最大熵模型可以预测枢纽换乘客流，从而确定枢纽规模等指标[1]并且为规划方案提供合理依据[2]. 用最大熵原理预测枢纽站换乘客流，将交通分布的预测方法应用到预测枢纽换乘客流上，该方法的优点与其它预测枢纽换乘客流的模型相比，不存在使用条件限制或考虑因素不足等问题，在模型中对未来的情况不做主观想象，保留了所有不确定性.国内外在此方面进行过一些研究[3-6]. 本文在此基础上对最大熵模型进行应用，重新构建了预测换乘客流量的最大熵模型，应用实例进行对比分析，并用真实数据进行修正，最后应用此模型预测大连北站2020年各交通方式之间换乘客流量.

1 模型的建立及检验

最大熵模型的建立首先需要确定系统内各种可能出现的不确定性[7]，然后通过推导得出以最大熵为目标函数，各种状态发生概率为自变量的数学模型，从而得到在最大熵条件下每种不确定情况发生的概率.对于枢纽换乘客流预测来说，资源配置的条件是要满足客流需求，所以首先要确定换乘发生和吸引的概率，然后通过引入重力模型，建立一个以最大熵为目标函数的，各交通方式换乘发生和吸引概率为自变量的数学模型.在完成模型的建立和相关参数的确定后，可以根据实例对结论进行检验，从而确定本文得到的结论具有普遍适用性.

1.1 模型建立

设Xi为交通方式i在目标规划年的换乘产生旅客数；Yi为交通方式j在目标规划年的换乘吸引旅客数；Xij为目标规划年交通方式i,j间的换乘旅客数.目标规划年交通方式i的换乘发生概率为fi,交通方式j的换乘吸引概率为gj, 由交通方式i向交通方式j的选择概率为hij.X为规划年换乘旅客发生总人数.X,Xi，Yi已知量，hij为变量[8].然后应用重力模型得：

式中,qij为引用重力模型时产生的先验概率;cij为相关重力模型系数;α为回归系数.

对换乘旅客出行总量X进行任意分布，分配到各种换乘交通方式之中.E为产生的组合数表示为：

(3)

将重力模型产生的先验概率qij引入式(3)，得到各换乘方式之间客流分布的概率[9]并令L=lnF得到式(4).解上述规划问题,求对数hij的拉格朗日方程.整理得到预测枢纽换乘量的最大熵模型为式(5)，于是各交通方式之间换乘人数为式(6)

式中，系数μ和λ是应用拉格朗日方程时产生的系数，与约束条件有关，需要通过对约束条件进行反复收敛来获得.

1.2 预测检验

选取实例对公式进行检验.选取北京市核心区域的东直门枢纽为例.该枢纽是北京最大的综合交通换乘换乘枢纽，共有20余条公交车站，3条地铁站在此交汇，现有旅客换乘规模约50万人次/天以上.过去该枢纽采用分散式布局，已经很难适应快速增长的换乘客流量需求.新建的西直门枢纽于2008年投入使用，占地15.44公顷，为亚洲最大的综合交通枢纽.枢纽地面层为公交换乘厅，地下层作为人流转运和地铁候车场所.除公共交通外，枢纽还设有大量的机动车和非机动车停车位，方便由私人交通向公共交通的换乘的旅客.

模型检验部分选择2008年东直门枢纽换乘客流量作为已知量，应用模型计算预测2010年该枢纽客流换乘量，并与实际值相比较，从而判断模型的准确性.2008年各交通方式之间换乘客流量及换乘总人数如表1所示.由于2008年西直门枢纽高铁站还处于规划阶段，为方便计算，数值取0.001[10].

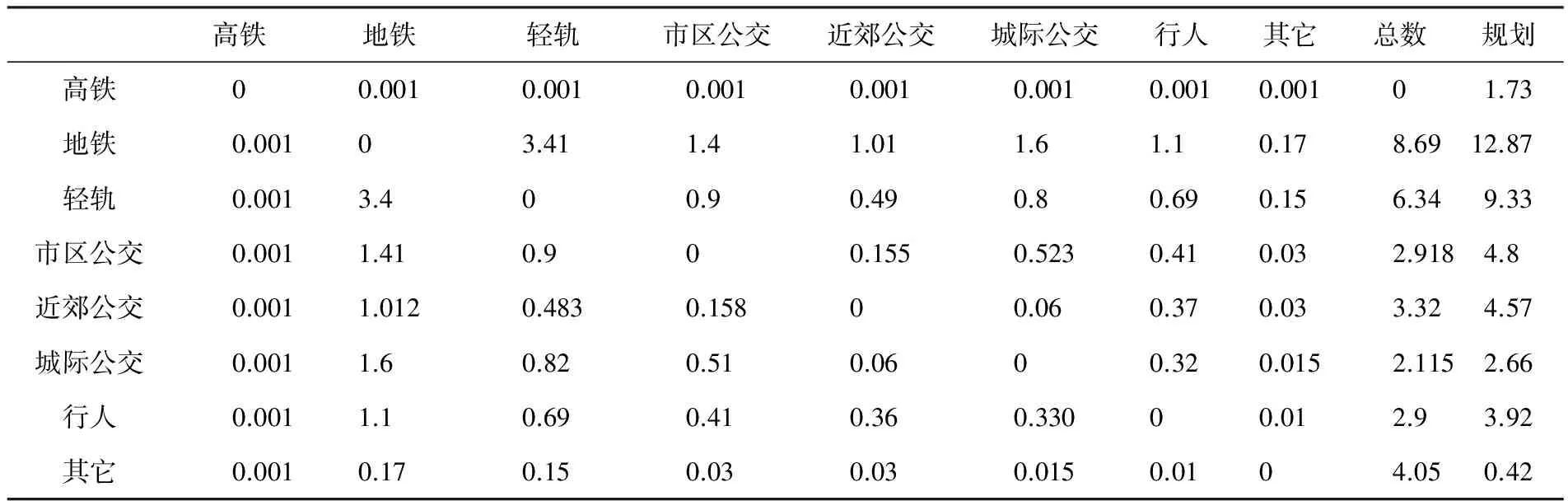
表1 2008年东直门枢纽换乘客流量 万人次/天

表2为乘客换乘各种交通方式时考虑的几种影响因素,如舒适度、运行速度、乘车费用、等候时间等.在舒适度指标中，1表示极其舒适、3表示舒适、5表示不舒适，2、4则表示中间值.确定这些影响因素的数据后，运用层次分析法确定各影响因素的权重，再根据权重计算得到各交通方式之间的出行阻抗cij.经计算得换乘的高铁的阻抗为55、换乘地铁的阻抗为20、换乘轻轨的阻抗为38、换乘市区公交的阻抗为42、换乘近郊公交的阻抗为58、换乘城际公交的阻抗为75、换乘为步行阻

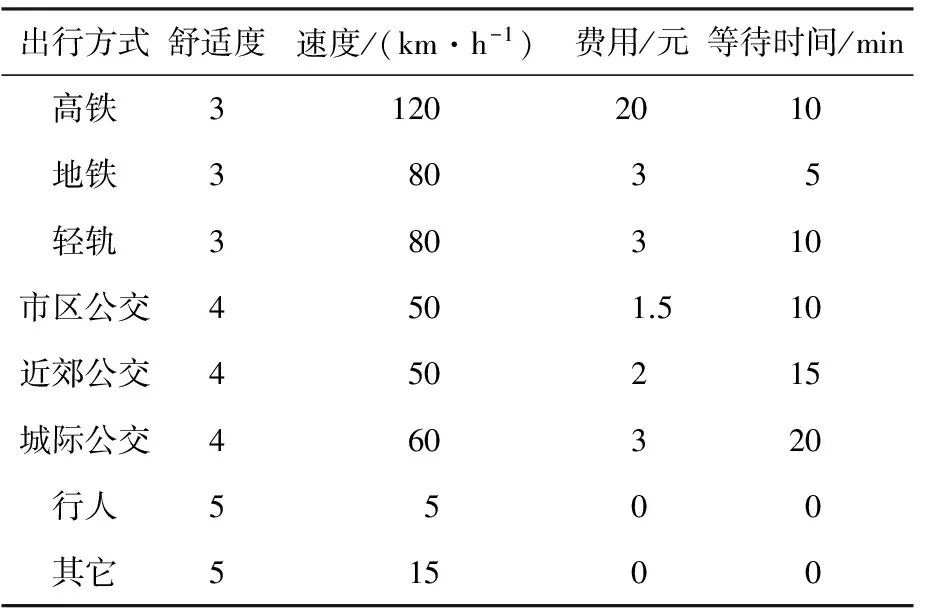
表2 各交通方式影响因素

抗为22、换乘其他交通方式阻抗为25.将规划年的日发生、吸引量数据及求得的交通方式之间阻抗代入式(5)、(6)中即可求得预测换乘人数.

将数据代入公式，并对约束条件进行反复收敛计算得到μi和λj的值，可求得的换乘矩阵如表3所示.计算值与表4所示真实数据进行对比分析，发现计算值偏小且误差过大，不具有实际应用价值，需要对模型进行调整.经过对模型的分析，认为需要对模型中的一些变量加入参数进行调整.

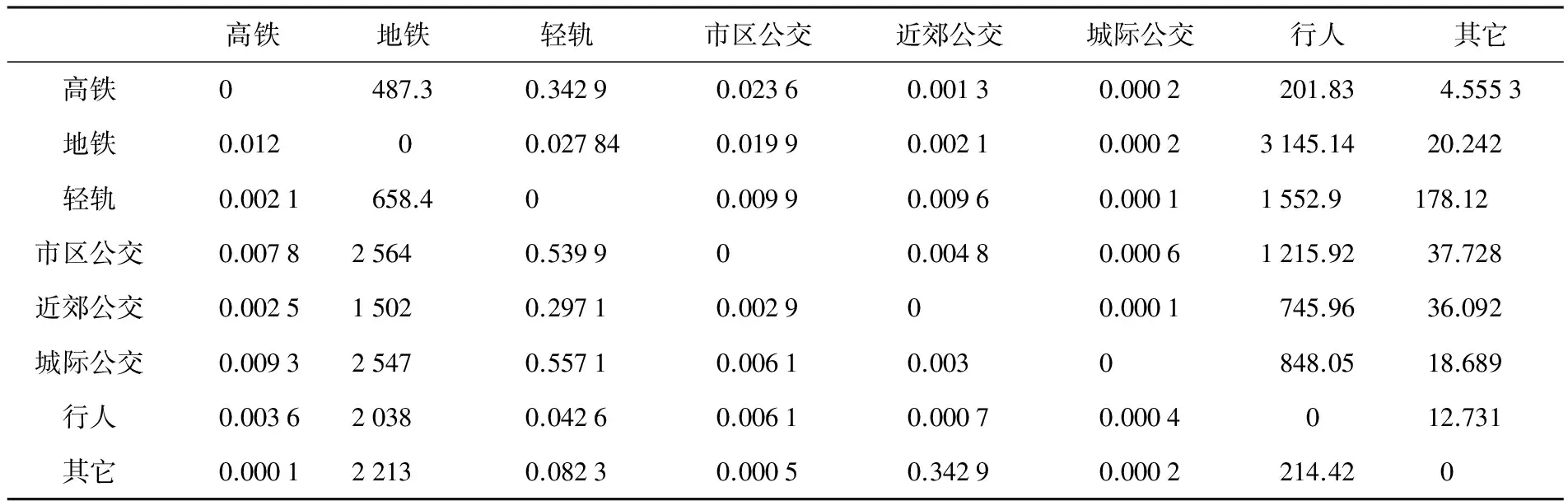
表3 换乘乘客流量 ×10-12万人次/天

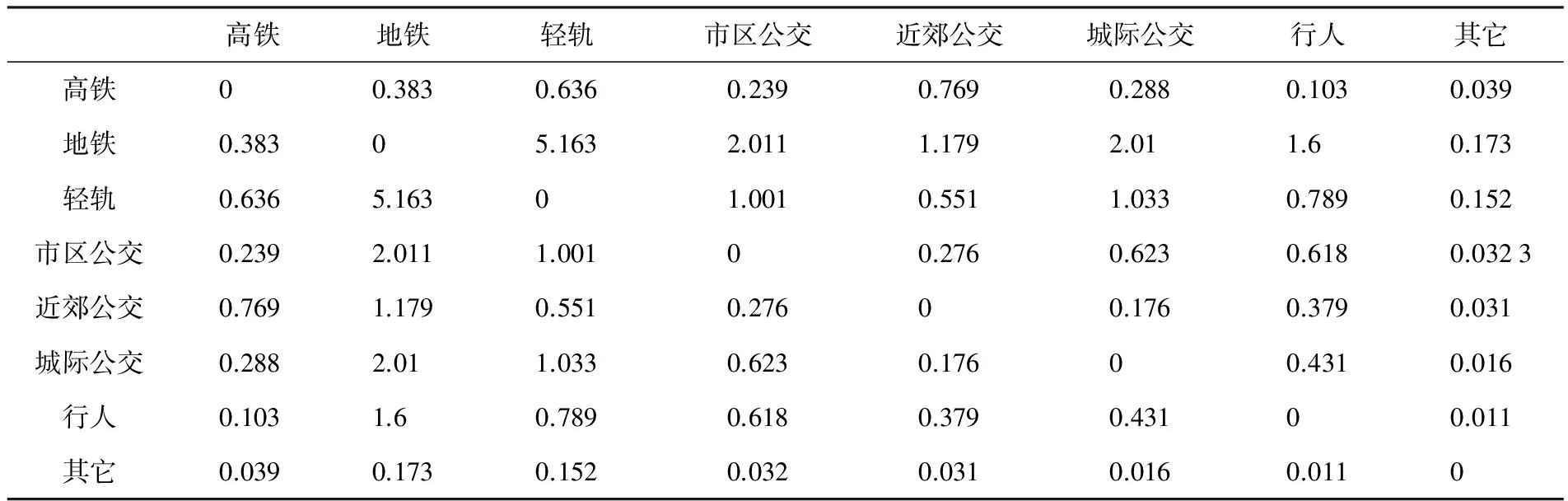
表4 2010年东直门枢纽换乘客流量 万人次/天

误差产生的原因是由于在公式推导中引用了重力模型.引用重力模型的目的是将已知的换乘客流总量分布到各交通方式中，在理论依据不变的前提下，可以在重力模型中加入参数作为调整系数，对重力模型进行修改使之在本文中更加适用.

分析式(2)，各参数均为已知量，只有cij是人为加入的变量，可能出现误差.故在cij前加入参数γ，在e的指数函数前加入修正系数φ，表示为φe-γcij.式(2)最终可以表示为[11]：

qij=αfigjφe-γcij

(7)

同理，可得到最大熵模型如下

(8)

至于公式中的参数φ，γ可以根据上述例子中实际数据进行反推得到.将表1～表4规划年的发生、吸引量数据，日各交通方式换乘量，日换乘总量代入式(5)和(8)中.经过计算可以得到36组相近的φ，γ值，如图1所示.对数据进行拟合，结果φ取0.024 01，γ取0.032 1.将所有求得的φ，γ值作为已知量代入模型检验，最终得到最

图1 参数变化折线图

接近实际值的结果如表5所示.经过对比计算所有换乘方式预测数据与实际数据的误差都在11%以内，误差可以接受.

表5 根据模型计算换乘流量 万人次/天

应用最大熵模型的优势是可以从宏观角度将枢纽内客流量化.应用模型的目的就是忽略枢纽不同，所在地域的差别和乘客换乘时的主观选择等因素的影响[11].因此，最大熵模型在各个枢纽的换乘客流预测中都可以应用.应用该方法再次对北京西直门[11]枢纽2009年换乘客流[12]进行计算，并对标定的参数φ和γ进行了检验，如图2所示.对比图1与图2可以发现每组参数的变化范围很相似；波动情况也很相似，可知模型具有广泛实用性[12].

图2 西直门枢纽参数变化范围

2 实例分析

大连北站位于大连市市区北部，北郊华北路北侧，南关岭街道，是我国东北地区重要的铁路车站之一，于2012年12月1日正式投入使用.大连北站建设面积为6.85万m2，面积相当于现大连站的4倍；候车大厅建筑面积2.4万m2，面积相当于现大连站的3倍，可同时容纳近万人候车的同时也可以满足候车人员休闲，娱乐，购物等要求.大连北站设10台20线，为东北地区规模第三大火车站.未来烟台至大连跨海隧道建成通车后，大连北站将成为东北地区连接山东和华东地区的最大铁路枢纽.

选取大连北站为研究对象，根据现有旅客换乘情况，应用最大熵模型预测2020年各交通方式之间换乘客流量.对几种换乘方式的运行速度，等待时间，乘车费用，舒适程度四个因素进行分析，并给出相应的数据，如表6，并用层次分析法确定各换乘方式的权重[13]，进而算出各种换乘方式的阻抗：换乘高铁的阻抗为22、换乘地铁的阻抗为20、换乘公交的阻抗为41、换乘出租车的阻抗为71、换乘社会车辆的阻抗为38、换乘其他方式的阻抗为12.

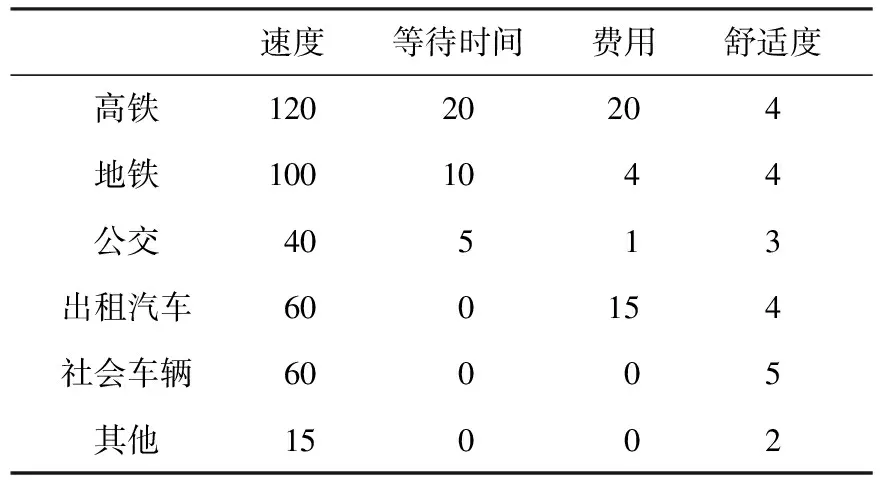
表6 各出行方式影响因素

得到各交通方式之间的阻抗后，根据表7的现状换乘量矩阵和规划年发生，吸引量[13]代入公式(6)～(8)，求出每种交通方式之间对应的换乘量，如表8所示.

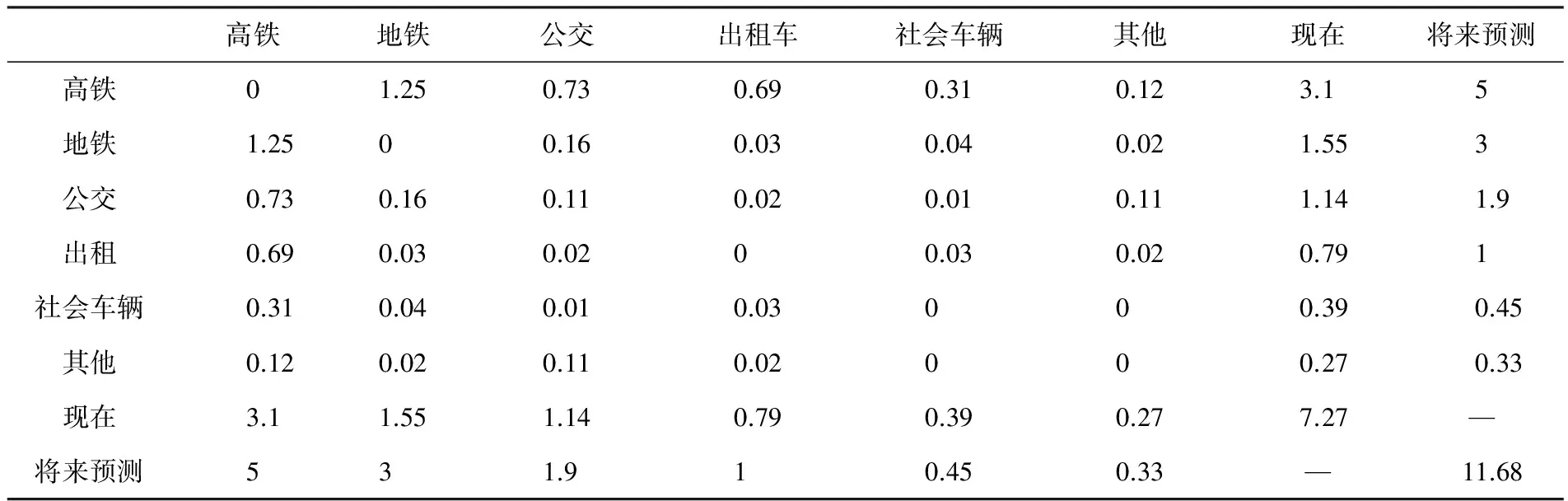
表7 现状换乘矩阵及总数 万人次/天

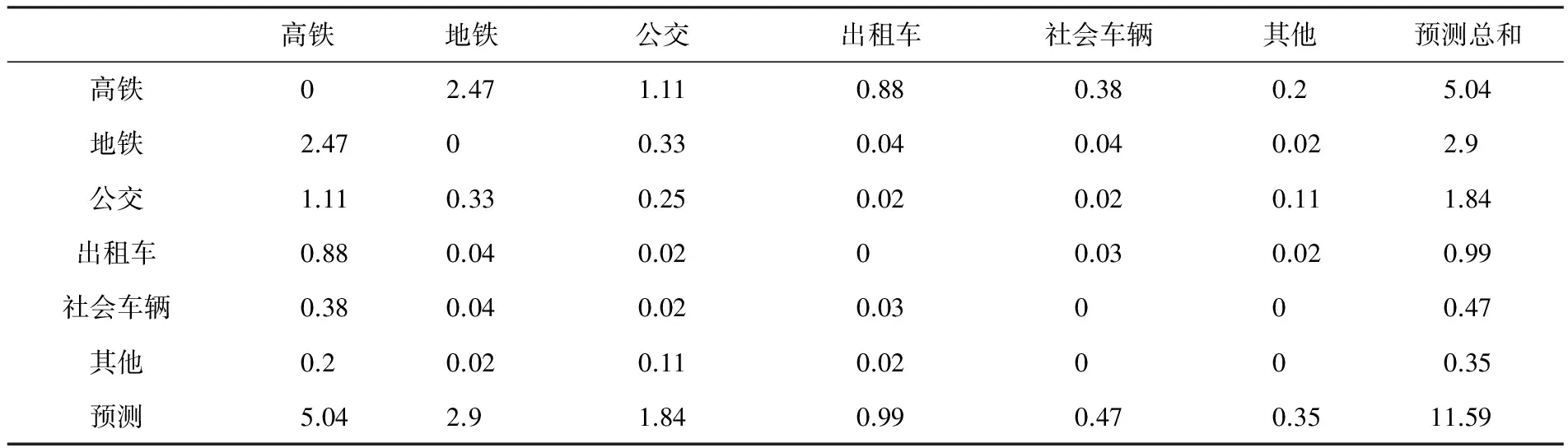
表8 2020年规划年换乘矩阵 万人次/天

计算结果显示，大连北站中高铁换乘客流量最大，其中高铁与地铁换乘客数量达到2.47万人次/天；地铁与公交客的换乘流量远大于出租车、社会车辆和其他；公共交通与出租车、社会车辆的换乘偏少，说明乘客偏向公共交通方式出行[14].由实例可以看出应用新构建的最大熵模型预测客运枢纽换乘客流量可以有效规避常规算法的弊端来进行准确的预测，且计算简单，可以运用到实际预测中.

3 结论

本文提出将最大熵模型作为预测枢纽内换乘客流量这一重要指标，保留了乘客的换乘的随机性的同时可以准确的预测出各交通方式之间的换乘客数.通过对方法原理的阐述和实例计算，可以发现该方法具有很强的实用性，原理简单，计算量较小，参数标定相对容易等特点，可以广泛应用于枢纽换乘客流的预测.

[1]JAMES F C, MORTON E O. Twenty-Five Years of Hub Location Research[J]. Transportation Science, 2013, 55 (3): 152-167.

[2]RENATO R, SVEINN V. Congestion spill effects of Heathrow and Frankfurt airports on connection traffic in European and Gulf hub airports[J]. Transportation Research, 2016, 92 (3): 155-159.

[3]魏丽英,崔裕枫,魏家蓉.基于局部最大熵换道规则的电动自行车流元胞自动机仿真模型[J].吉林大学学报,2016,41(6):1- 10.

[4]郑明明, 徐洪峰, 左忠义. 城市综合换乘枢纽的出租车合乘调度方法[J]. 大连交通大学学报, 2017, 38(3):1- 6.

[5]曹弋, 杨忠振, 左忠义.基于地铁停车换乘的区域差异性停车收费策略[J]. 大连交通大学学报, 2017, 17(3):12- 18.

[6]常玉林, 陈向宇. 最大熵模型在公共交通分布预测中的应用[J]. 科学技术与工程, 2015, 15(3):285- 288.

[7]左忠义, 杨广川, 邵春福. 基于公交优先的小汽车出行向公交转移模型研究[J]. 交通运输系统工程与信息,2012,12(1):24- 30.

[8] 邵春福. 交通规划管理[M]. 北京: 中国铁道出版社, 2008.

[9]孙立山, 姚丽亚, 荣建, 等. 基于最大熵模型的客运枢纽换乘量分布预测研究[J]. 公路交通科技,2008, 25(9):140- 144.

[10] 张忠国, 徐婷婷, 解宏涛. 城市公共交通枢纽换乘空间问题分析-以北京西直门交通枢纽为例[J]. 城市发展研究, 2009, 16(1):120- 126.

[11]何南, 孟可欣, 张美娇, 等. 城市轨道交通网络的同步换乘模型研究[J]. 大连交通大学学报, 2016, 37(4):1- 4.

[12]宋双双, 左忠义. 基于DEMATEL-ANP与熵权的社会风险评价指标权重分析[J]. 大连交通大学学报, 2016, 37(3):1- 5.

[13]贾洪飞, 宗芳, 乔路. 综合客运枢纽换乘量预测方法[J]. 系统工程, 2009, 27(1):15- 19.

[14]左忠义, 李鑫. 城市轨道交通系统的适用性评价[J].大连交通大学学报, 2015, 36(增刊1):1- 4.