基于焊接式结构吊环有限元处理方法研究∗

2018-03-21廖建敏冯灿波

风机技术 2018年1期

廖建敏周舟,3 朱畅冯灿波

（1.湘电风能有限公司；2.海上风力发电技术及检测国家重点实验室；3.湖南省风电装备与电能变换协同创新中心）

0 引言

大型机械化装备作业在能源、化工、电力等行业使用较为普及，受大型装备的装配、运输以及安装不易等限制，通常需要在相应设备上加工有便于吊装的吊环[1-3]，吊环的承载主要为吊运构件的自重。对结构较为复杂的大型铸件其吊环结构一般与铸件连成一体通过铸造而成，例如风力机组中轮毂、机舱等，而常规吊环加工处理方法主要还是通过后期的焊接板形式来获得，板材的结构尺寸在满足承载能力的前提下，要确保所需的焊缝焊趾高度不能过大，以免使焊接热应力影响原有构件的初始应力状态。传统的设计方法中，吊环设计主要基于理论公式以及相关设计手册来完成，通过对某一危险工况下的载荷计算，获得满足强度及刚度要求的结构尺寸。当然为了较为直观地显示整体应力情况，目前更多学者采用了有限元计算方法，文献[4-6]就分别对两种新设计的专用吊环进行了有限元分析。

整个吊环承载关键在于吊环的圆形孔处以及焊接位置处，上述文献中对于吊环力的加载方式主要是通过半圆环面施加压力或集中力，然而在实际工程中联接于吊环的支撑件圆形截面不可能与吊环圆环是全等的，存在一定的偏心，所以实际两者的接触关系在初始位置属于线接触，在受力作用下才会发生变形，由线接触变成面接触。因此直接采用半圆环面加载方式与实际受载情况明显不符合，同时在对焊接板吊环结果处理时，焊缝位置处的应力状态，对工程应用有着较为重要的依据。本文基于焊接板形式吊环，建立了一套较为完善的有限元分析方法，对吊环的结构设计具有一定的理论指导意义。

1 分析要求

以某海上风机140-4MW机型中二段塔筒平台吊装所用的支腿吊环为研究对象，如下图1所示，该吊环由两块板焊接而成，分别为底部固定板及支撑板，支撑板上吊环孔在承载过程中实际上是由支撑构件的圆柱体来传递，所以构件在力的加载过程中，吊环圆环面受力会由线接触向面接触过渡。

图1 海上风机支腿吊环Fig.1 Offshore wind turbine leg

在实际应用中，吊环常见的破坏形式主要有三种：吊环面发生磨损、支撑板被拉断、焊接位置发生断裂[6]，要确定吊环能否发生上述三种破坏情况，只进行单一载荷作用下的静力学分析，很难保证结果的可靠性。基于上述三点考虑，结合有限元分析要求，为有效判断吊环面是否发生磨损以及支撑板是否被拉断，通过建立接触对的方式进行分析，忽略板件之间的焊接，将其简化成刚性连接；为判断焊接位置是否会发生断裂，则简化吊环处的加载方式，建立焊接模型进行分析。

2 吊环接触分析

2.1 接触分析方法

吊环所承受力的作用实际是通过吊钩来传递，根据Hertz理论吊钩与吊环的截面半径对变形接触面积以及接触压力有较大影响，Hertz理论采用的是理想弹性体的无摩擦接触，在分析材料的线弹性阶段有较大优势，因此本文首先经Hertz经典理论进行吊环接触分析。在Hertz理论关键因素是提出的假定接触变形体的产生接触压力与变形接触面所形成的半球面纵坐标成正比[7]，在本文分析模型中可看成柱面接触，其受力如下图2所示。

图2 球体与球座接触模型Fig.2 Contact model between sphere and base

受载荷p的作用，柱面会产生变形，接触类型将由线接触转化成面接触，面接触的接触宽度为2b，由变形导致轴线距离发生δ大小的变形量。利用弹塑性力学可将该问题简化成是半无限平面受分布载荷的作用[9]，通过半无限平面受集中载荷的计算方法进行分布载荷积分计算。

结合Hertz理论假设方法，通过弹塑性力学平面集中载荷下应力位移计算方法，获得弹性圆柱体接触问题计算公式：

接触面宽度：

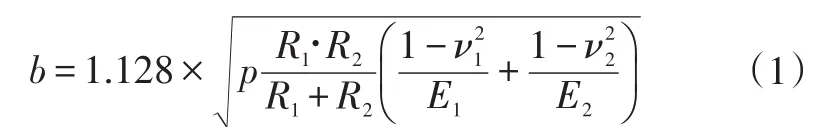
最大接触压力:

轴线中心距压缩量:

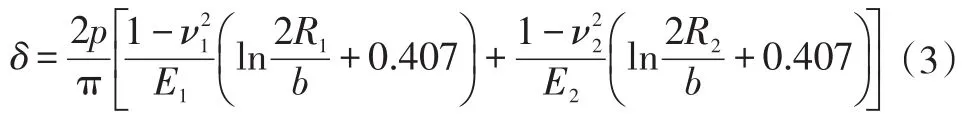
根据上述公式可得出，保证吊环直径不变情况，吊钩的直径越接近于吊环直径，变形产生的接触宽度越大，变形形成的接触压力就越小，所以在吊环设计过程中，吊钩与吊环直径大小理论尺寸基本相同，保持同心，但是考虑配合需要，还应允许有一定的间隙量，本文经有限元数值计算方法得出具体允许间隙量大小。

有限元接触算法主要有：直接迭代法、Lagrange乘子法、罚函数法以及变分不等式法，其中罚函数法对目标寻优以及非线性问题有较为突出的优势[8]，被广泛应用于有限元分析计算，本文所采用的分析软件再接触计算方面采用的是上述方法。罚函数法主要是在原有的Lagrange乘子法基础上添加了惩罚因子，得到的力与形变位移关系如下：

式中，pn为法向力；ps为切向力；ΔUn为法向位移增量；ΔUs为切向位移增量；En，Es为惩罚因子。

该式中代表的是接触边界单元刚度矩阵，根据有限元方程[K]{U}={F} ，通过位移边界条件，可得出接触单元节点应力值，所以以罚函数进行的接触计算，惩罚因子的选取较为关键[9]，过小不容易收敛，过大会造成病态刚度矩阵，文中综合考虑接触穿透量及结果计算收敛性选择惩罚因子为3。

有限元对接触分析属于非线性问题，在进行计算时需要确定接触的两个关键因素才可确保接触分析结果准确性[10]，分别为：接触类型和接触方式，接触的类型有刚体-柔体接触和柔体-柔体接触两种，吊环与吊钩两者都属于变形体，所以需要作柔体-柔体接触处理；接触方式有点-点接触、点-面接触或者面-面接触等，对于两者都为圆柱体的接触，在加载之前属于线接触，受载荷作用产生的变形使得接触由线接触向面接触过渡，因此在选择接触单元应为面接触单元[11]。由于接触面为圆弧边线，在有限元网格单元的离散化，圆弧边线转化成多边形边线使得在划分网格单元后，原先接触边界发生分离，因此在划分网格后需放大接触边界搜索值即设置Tolerance value大于5mm。

2.1 网格划分及边界加载

采用Solid Works软件分别建立吊环以及支撑件承压截面模型，导入到workbench软件中进行静力学分析。根据风机塔筒平台的安装要求，吊环的固定板通过螺栓连接固定于平台面上，因此对四个螺栓孔处施加fixed support固定约束。支撑件（如图1所示）柱面在承载过程中只发生微动，对圆柱接触面施加displacement切向转动约束。在焊接接触面设置bond绑定接触，而在受力接触面考虑允许法向可分离，切向允许有微小滑移，设置为frictionless无摩擦约束。该吊环设计要求最大满足5t的承载力，对吊环连接件圆环截面施加50kN的集中力。

2.2 支腿吊环结果分析

根据应力云图可看出，若支撑件截面圆环与吊环面有偏心，吊环在吊装过程中最大应力主要集中于两者接触面端面附近如图3（a）所示，最大应力为50.453MPa，满足屈服强度要求，该位置可说明吊环在长期使用过程吊环两侧圆环面可能会发生较为严重磨损，与实际应用中吊环表层易发生金属脱落现象类似，验证了该分析的可行性。

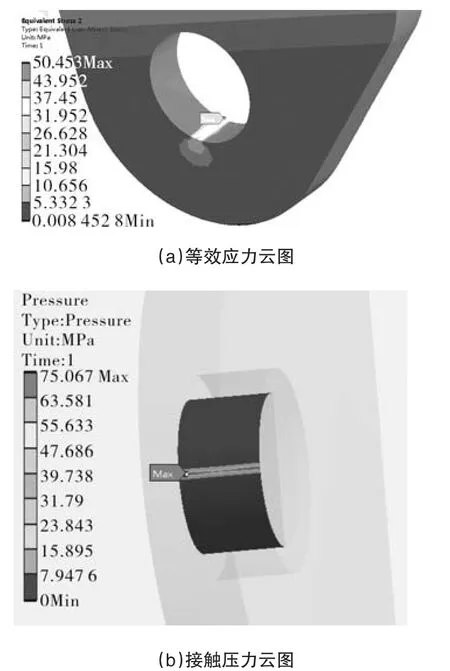
图3 吊环有限元分析结果Fig.3 Lifting sling FEA result

根据接触面的接触压力云图（如图3（b）所示）可发现，最大接触压力位置主要发生在构件的边缘处，所以若吊环在长时间的运行状态下，相互接触表面容易发生接触疲劳破坏，在吊环边缘形成表面裂纹，与实际使用情况较为贴合。接触压力大于0表示支撑件与吊环发生实体接触，说明支撑件发生变形，则力传递由线接触转换为面接触，通过提出圆环面接触压力坐标值，得出发生变形的圆弧面弦长度为2.354mm，而根据Hetrz经典接触理论公式（1）所得出的接触变形宽度为3.2mm，与有限元数值计算结果明显偏大，这是由于理论计算基于简化二维模型，而有限元建立的为三维模型，沿轴向厚度方向形成的平面应变状态影响接触变形量。同时受轴向平面应变的影响，使得沿厚度方向上接触变形量并不保持一致，改变轴向接触应力分布。根据接触分析的结果，该结构不会出现接触强度破坏以及磨损破坏。

2.3 接触分析

根据上述可得出，接触面积的变化影响吊环面应力分布，而影响接触面积变化除加载力数值变化最主要的还是支撑构件圆环截面直径，因此为获得支撑端面半径对接触长度影响，保持加载力的大小不变，对半径分别为16mm、17mm、18mm、19mm这四种情况下接触面积进行分析计算，获得如下半径与接触面积变化曲线。

图4 接触长度曲线Fig.4 The curve of contact length

从上图4可得出，随着圆环直径的增大，圆弧接触长度也逐渐增大，但在半径小于17mm时增大幅度较小，从17mm后接触长度出现陡增，然后增大幅度又趋于平缓，说明当半径趋近于吊环半径值，半径对接触变形影响较小。由于接触长度的增大可以有效减少最大应力位置处的压力承载，对减缓该处的应力值有较大改善作用，因此对于该支腿吊耳支撑件圆环面与吊环配合可允许有2mm偏心。

3 焊接处理方法

通过获取焊缝位置拐角处的应力值，发现此时的应力值明显偏小，最大值仅为7.18MPa，提取固定板处沿加载力方向的支座约束反力为2 167N，根据力系平衡原理，这是由于在考虑接触情况下对支撑件圆环面施加了径向约束，而抵消固定板处部分应力，说明此时在焊接位置处所传递的力系大概也处于上述值的附近，由此可以解释在焊接位置处应力偏小的缘故，而实际对于焊接部位所能承受的力基本是与加载力大小相同。因此，要想准确分析焊接位置处应力，则需单独对吊环面施加载荷，加载面的大小由接触分析所获得接触长度来确定，加载面通过Solid Works分割的方法获得。

3.1 焊缝分析

由于焊接位置处热影响区以及熔化区存在，使得在焊缝部位处于较为复杂的应力状态，因此采用何种应力评判标准来准确描述焊缝应力大小和位置是研究的热点，目前主要有名义应力法、热点应力法和切口应力法，其中热点应力法是与有限元法结合较为紧密的一类，分析不考虑构件宏观裂纹的存在，因其处理方法简单，参数控制容易在数值分析计算广泛采用。热点应力即为结构中危险截面上的最大应力，对于焊缝点其热点应力为焊趾部分应力，在有限元中对热点应力计算采用外推法[12]，其目的是避免焊趾尖端的非线性应力峰值，对焊缝处热点应力计算主要归结为两大类“a型：焊趾位于板的表面”和“b型：焊趾位于板的边缘”，其中a型热点外推计算方法：

1）设置焊缝位置处网格尺寸小于0.4t（t为焊缝厚度），选取离焊趾边缘0.4t和1t处的应力值，采用两点线性外推：σeq=1.67σ0.4t-0.67σ1.0t；

2）采用1）中所述网格尺寸，进行三点线性外推：

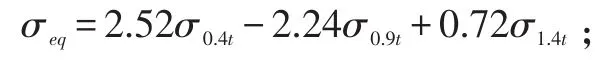
3）对于需要进行划分粗糙网格，其网格单元尺寸必须为板厚值，选取的焊趾参考计算应力值位置为0.5t和1.5t，进行两点外推：σeq=1.50σ0.5t-0.5σ1.5t；

b型热点其焊缝位于边缘处，实际焊缝产生的裂纹并不会形成穿透扩展，因此对于该类型应力分布不取决于板厚的多少，在进行线性外推时的参考点选择不需要结合板厚进行分析：

1）对于较高精度网格，选择的参考点位置为距离焊趾处4mm，8mm和12mm，进行三点外推：

2）对于粗糙精度网格，其统一为10mm网格单元的热点应力进行外推，具体选择参考点位置依据焊趾前两个单元的中间节点：σeq=1.50σ0.5mm-0.5σ15mm

3.2 焊缝处理结果

钢板焊接方式采用是填充式，其填充金属对于焊缝连接部分刚度有一定促进作用，因此为了分析的准确性，对焊缝模型进行建模，根据上述分析该焊缝类型为a型焊缝，因此本文采用网格尺寸较高的两点线性外推法进行焊缝热点应力计算，建立的焊缝网格模型如下图6所述，焊趾高度为5mm。有限元模型网格设置方法以及加载与接触模型相同。

分析结果如图5所示，从图中可发现，受吊环载荷作用支撑板底部以及固定板在焊缝端部位置出现受拉趋势，导致在支撑板焊缝位置处产生最大应力192.17MPa，安全系数为1.22。提取离焊趾水平两侧及上侧方向上的边缘0.4t和1t处的应力值，提取位置如下图6所示，提取后的应力值见表1，对3个方向的热点应力进行取平均值为193.874MPa。