离心压缩机回流器叶片的优化设计∗

尹熙文 王 剑 范永生 闻苏平 卢傅安 张鹏刚

（1.西安交通大学能源与动力工程学院；2.沈阳鼓风机集团股份有限公司）

0 引言

在多级离心压缩机中，回流器主要起导流作用，引导从扩压器元件中流出的强旋绕气流以轴向或特定方向进入下一级叶轮。研究表明，气体在回流器中摩擦损失很大，有时可达到级能量的6%～8%，对整个压缩机级的性能影响较大。而且回流器出口的气流可直接影响下一级叶轮的性能，因此改善气流在回流器中的流动十分必要[1]。Veress等人[2]提出了一种离心压缩机回流器反设计与优化的方法。Nishida[3]采用遗传算法对离心压缩机回流器进行了多目标优化，使效率和压力系数分别提升了1.0%和3.2%。Glass等人[4]研究了回流通道的损失机理，通过优化回流器通道子午型线达到了减少损失的效果。Hildebrandt等人[5]运用优化算法对一个多级离心式压缩机弯道和回流器进行三维优化设计，优化后回流器总压损失降低了3%，总压损失系数从0.825降到0.627。Fakhri S等人[6]对离心式压缩机级的固定原件进行优化设计，发现没有经过优化设计的固定元件，很容易因低能量区的流动形成脱离团，从而导致喘振过早发生。鲁业明等人[7]对离心压气机弯道和回流器的结构进行改进，弯道采用截面面积变化率为常数的设计方法可以提高总压恢复系数、改善出口流场分布。范永生等人[8]通过改变回流器叶片载荷控制参数K5，形成不同的回流器叶片型线，数值研究了不同载荷分布下的回流器叶片对基本级性能的影响。

近年来随着优化理论的快速发展以及优化方法在工程上的大量应用，出现了如遗传算法、基于梯度的优化算法和模拟退火算法等优化算法。将这些优化算法和CFD技术结合起来就形成了一种新的叶轮气动优化设计方法。优化设计方法的步骤为：设计人员首先根据经验和实验数据进行设计，然后对叶轮子午结构及叶片几何进行参数化建模，选择这些参数中的适当参数作为优化变量，将多变效率、压比以及气动结构上的约束作为优化目标，在优化变量的取值范围内搜寻优化目标的最优值。

由于现代设计技术中CAD（Computer Aided Design，CAD）和CAM（Computer Aided Manufacturing，CAM）的发展，国内外大量的研究人员对三元叶轮的设计进行了广泛、大量和充分的研究[8-9]，经过多年的探索，三元叶轮的效率已高达95%，进一步提升的空间已经非常有限，所以研究者将研究方向从叶轮转向扩压器、弯道和回流器等静止部件上。回流器作为多级离心式压缩机级间的连接部件，对气体流动起到承上启下的作用。一方面对从弯道流出的气流进行整流，减小气体的周向速度，提供一部分压升，另一方面使流经回流器的气体在通过级出口弯道后尽可能的均匀，以减少气体进入下一级叶轮进口气体预旋。由于离开扩压器气体是强旋绕气流，这样回流器叶片必须以尽可能小的损失消除非常高的气体旋绕。传统的回流器叶片均是二元叶片，不能很好的控制流场，本文以基本级D-ARV为研究对象，对回流器叶片进行优化设计。

本文通过基于商业流动计算Numeca与人工神经网络ANN以及遗传算法GA相结合的优化方法，对离心式压缩机基本级R回流器叶片上、下中型线、叶片厚度进行了优化设计，优化后叶型折转角β变大，径向产生正倾角。

1 数值研究

1.1 基本级描述

基本级R流量系数φ1=0.02，叶轮为三元叶轮，叶轮叶片进口直径D1为210mm，出口直径D2为450mm，叶轮出口宽度b2为10mm，叶片数为17，带叶片扩压器，扩压器出口直径D4为616mm，扩压器叶片数为15。工作介质为空气，机器马赫数Mu=0.9。进口压力pin=98kPa，进口温度Tin=293K，设计质量流量Qm=1.177kg/s。

1.2 回流器的主要结构参数

离心压缩机基本级R回流器主要结构参数见表1。

表1 基本级R回流器主要结构参数表Tab.1 Main structural parameters of return channel of basic stage R

1.3 回流器三元叶片参数化建模

由于在对叶片参数化建模的过程中会有几十个甚至是几百个参数产生，所以在优化过程中不可能将所有的参数选择为优化变量，这样会使得样本生成时间大幅度增加，导致优化无法继续。因此这就涉及到应该如何选择适当的优化变量来进行优化问题的求解，根据所选择优化目标的不同，优化参数的选择也会不同。

影响回流器性能优劣的几何参数有很多。选取回流器叶片中弧线和叶片厚度沿弦长的分布为主要参数，确定回流器叶片的叶型。回流器叶片特征位置包括叶片的子午位置及周向位置。在流体机械中，通常采用一个参考点（也可以说积叠点）来定义一个二维叶片截面在一个流面的位置，子午方向前后掠和周向倾斜采用两个不同的曲线控制即可。如图1所示，回流器叶片根、顶截面上分别需要5个控制点定义中弧线来表达叶片角沿弦长分布和7个控制点来表达叶片厚度沿弦长分布，一共24个设计变量。其中，叶根中弧线控制点为Ah/s,i（i=1，2,……,5）；叶片厚度控制点为Bh/s,j（j=1，2,……,7）。

图1 回流器叶片参数化建模Fig.1 Parametric modeling of return channel blades

优化进行之前，需要建立一个包含几何结构以及与之相对应的CFD计算的优化目标数据库，对优化的实施来说这是很重要的一步，并且这一步骤要占据优化过程的大部分时间。CFD计算的物理条件与数值条件的选择对初始数据库的产生来说也是非常重要的，因为在整个优化的过程中这些值都是保持不变的。

参数取样通过采用离散层取样的方式产生混乱的几何，一般按照总样本空间覆盖率20%或者按总自由参数个数的3倍进行选取。在样本的生成过程中，由于样本的数量大，本文设置不同的初始索引号在不同的机器上分别生成样本，再将不同样本的数据库进行合并。

1.4 优化设计结果

回流器内气体流动复杂，能量损失很大，因此将基本级多变效率ηpol作为评价能量损失的目标函数：

同时，为了保证回流器的变工况性能，要求静压恢复系数在流量系数φ1研究范围即0.014～0.026时，均大于0.25。其中，静压恢复系数的定义为：

式中，ps表示静压；pt表示总压。

在优化过程中，合理的变量寻优空间对于优化设计来说是很重要的，寻优空间对优化时间有着决定性的影响，寻优空间太大会加大优化时间，而空间太小就只能在空间范围内找到最优值，而不是真正的最优值。优化进行30代迭代后基本收敛。从得到的一系列优化样本中选取一个样本并将优化变量、寻优空间以及优化变量的值列于表2。

表2 回流器优化变量、设计空间及优化参数结果Tab.2 Optimal variables,design space and optimal parameters results of return channel

回流器叶片经优化后，在设计流量工况下预测的性能见表3。将优化后配置回流器三元叶片的基本级R称为基本级R-X，基本级R-X多变效率ηpol达到84.24%，比优化前提高了1.07%，总压比εT为1.88，提高了1.62%。

表3 回流器优化后的性能对比表Tab.3 Performance comparison of return channel after optimization

图2 回流器叶片优化前后对比Fig.2 Comparison of return channel blades after optimization

图2是回流器叶片优化前后结构对比图。从图3可以看出，优化后，回流器叶片发生扭转，呈现典型的三元结构，回流器叶片的叶根、叶顶的折转角β均比原结构小；相比之下，叶根减小的更多，叶根进出口折转角略微小，叶顶进出口折转角β略微增大；叶片折转角β最多减小了13.76°，叶片厚度也相应减小，最多减小了4.47mm，最大厚度减小幅度不大，除了叶顶叶片尾缘厚度增大，叶根、叶顶叶片前缘、尾缘厚度基本保持不变。

对基本级R-X进行数值性能预测。预测的级性能结果如图4所示。从图3可以看出，优化后级多变效率ηpol在流量系数φ1为0.026时提高了4.16%，总压比εT提高了1.16%。

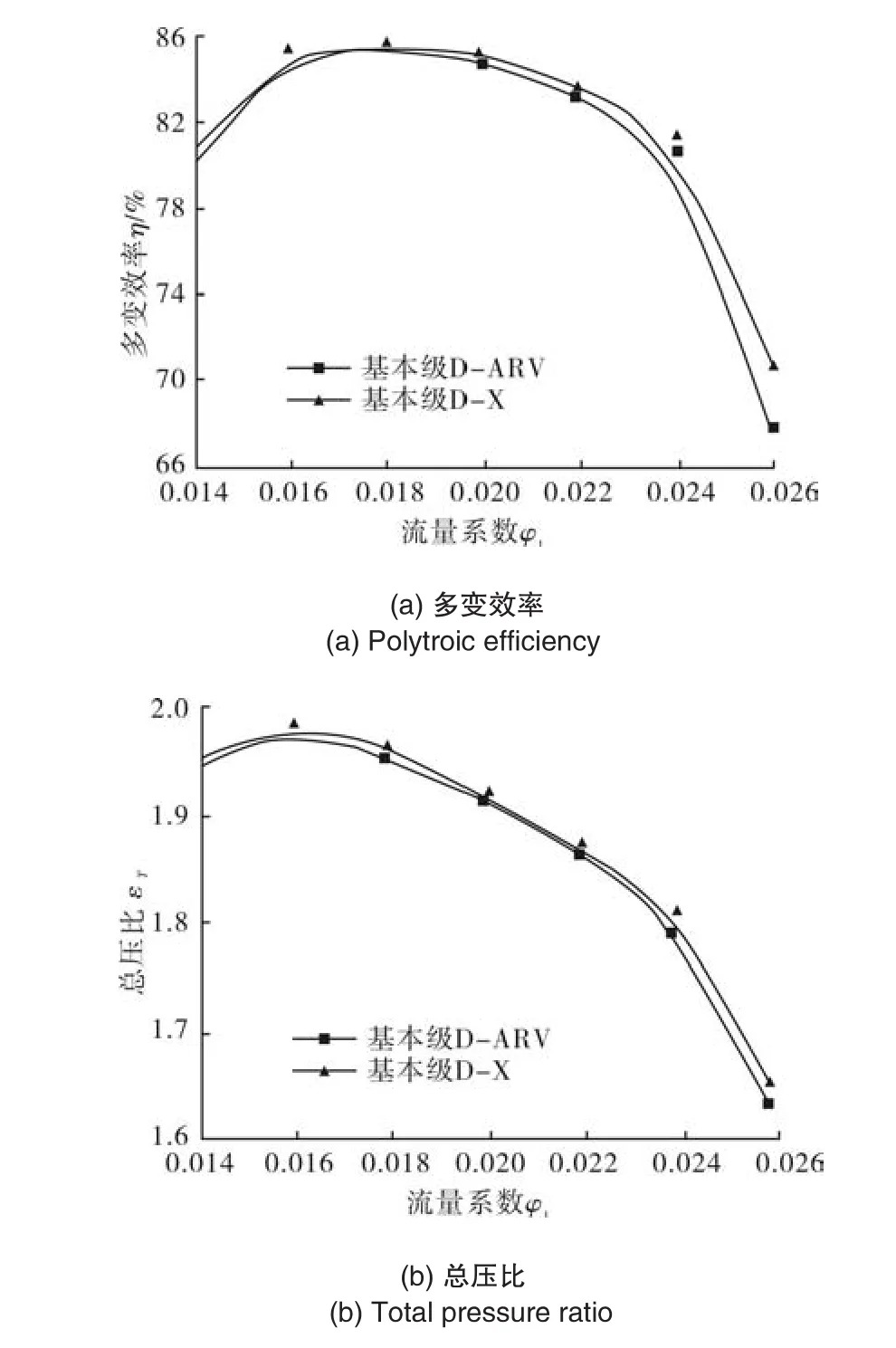
图3 优化前后性能对比Fig.3 Comparison of stage performance curves after opimization

2 结果与分析

通过上一节分析可知，优化后的三元回流器在整个工况范围内显著提高了整级性能。本节进一步对优化前、后气动结果进行对比分析。为了更好地了解气流在回流器中的流动状况，对回流器内部截取r=306mm、289mm、271mm、254mm、237mm、219mm、202mm、185mm、167mm和150mm共10个不同的截面，并将这10个截面分别命名sectioni（i=0，1，2，……，9）。截面具体位置如图4所示。

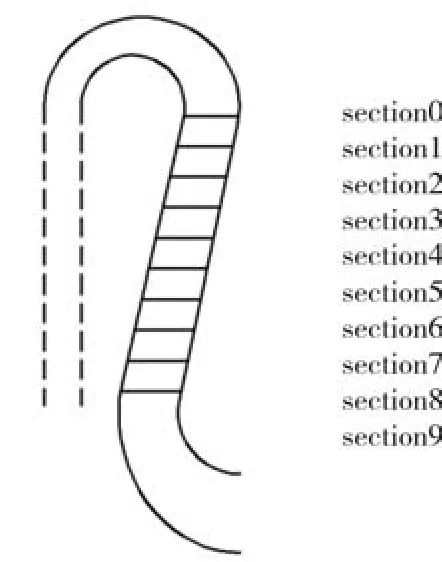
图4 回流器子午面截面分布图Fig.4 Distribution of the meridional plane sections of the return channel

以下对不同工况下回流器流道内部各个截面流动进行数值研究。

2.1 设计流量

图5提取出三元回流器内10个截面的子午速度Vm并绘制到一张图进行对比分析。当气流方向经过弯道折转180°进入回流器，由于弯道曲率的作用，气流对回流器有影响，导致气流在回流器进口段轮盖区域速度比轮盘区域大。随着气流向下游发展，回流器半径减小，子午速度Vm逐渐增大，并且气流从截面0流经截面5,从轮盖侧到轮盘侧面的速度差逐渐减小，气流逐渐均匀；气流从截面5流经截面7,子午速度Vm非常均匀，在截面8处，子午速度Vm表现为轮盘侧稍大于轮盖侧；回流器出口截面9的子午速度Vm达到最大，相当于气流的子午速度Vm在回流器内得到加速，以便提供一定动能的气流进入下一级叶轮。

图5 三元回流器内不同截面处Vm沿叶高分布Fig.5 The distribution ofVmalong the blade height in different sections in the three-dimensional return channel

图6为三元回流器内不同截面Vt沿叶高分布图。从截面0到截面9，回流器叶片起到整流作用使周向速度Vt逐渐减小，使得强预旋气流流动逐渐均匀。截面0处的周向速度Vt表现为：从轮盘侧到半叶高周向速度Vt从小到大变化，在半叶高附近周向速度Vt达到最大，从轮盖到半叶高速度变化和轮盘侧到半叶高类似；从截面0处到截面9，轮盘（盖）侧到半叶高周向速度Vt变化基本一致；所不同的是，从截面0到截面9，轮盘（盖）侧和半叶高处周相速度Vt大小值之差和变化率逐渐减小；周向速度Vt在回流器出口端达到最低，并且在截面8和截面9的轮盘、轮盖区域有负速度，说明这两处有回流存在，造成损失。

图6 三元回流器内不同截面处Vt沿叶高分布Fig.6 The distribution ofVtalong the blade height in different sections in the three-dimensional return channel

图7展现了三元回流器内不同也截面气流角α沿叶高分布，从截面0到截面9逐渐减小，回流器进口处截面0的气流角相对均匀，最大气流角出现在轮盘附近，气流角沿轮盘侧向轮盖侧逐渐减小；随着气流向下游发展，截面最大气流角从轮盘侧向半叶高移动，并且轮盘侧气流角大小和轮盖侧气流角大小基本一致，气流角曲线线型近似于开口向下的抛物线；气流角在出口端达到最小，轮盘、轮盖侧小于0°，半叶高附近大于0°，出口状况理想。

图7 三元回流器内不同截面处气流角α沿叶高分布Fig.7 The distribution of flow angleαalong the blade height in different sections of the three-dimensional return channel

2.2 变工况

图8为基本级R和基本级R-X回流器内静压恢复系数-流量关系图。二元回流器和三元回流器的静压恢复系数CP随着流量系数φ1增大，先增大后减小，在流量系数φ1=0.02时，静压恢复系数CP分别达到最大。在整个工况范围内，三元回流器的静压恢复系数CP比二元回流器高。

图8 两种回流器静压恢复系数-流量关系图Fig.8 The static pressure recovery coefficient-flow rate curve of two return channels

图9为变工况回流器内周向平均径向速度Vr沿叶高的分布，由图可以看出，在变工况下两种回流器由于受到弯道的影响，导致盖侧径向速度比盘侧要高，一直到叶片中部，也就是从截面4开始，径向速度沿叶高速度趋于均匀，在1.3Qd工况下，三元回流器的进口轮盖侧径向速度更大；二元回流器在各个工况出口截面的径向速度相对于截面8小，主要表现为截面9轮盘侧到半叶高区域径向速度小于截面8。

图10为变工况回流器叶片半叶高截面速度矢量图。在0.7Qd工况下，三元回流器没有出现回流和流动分离，二元回流器在叶片凸面中下游有一个小范围回流，引起损失；在设计流量Qd下，三元回流器内部气体没有出现回流和流动分离现象，只是在回流器叶片凸面中下部有一个低速区，随着流量工况发生改变，有发生流动分离的可能，二元回流器叶片在叶片凸面中下部速度梯度较大；在1.3Qd工况，两种回流器均出现大面积回流区，都始于回流器叶片凸面中上部，造成损失，导致效率急速下降。

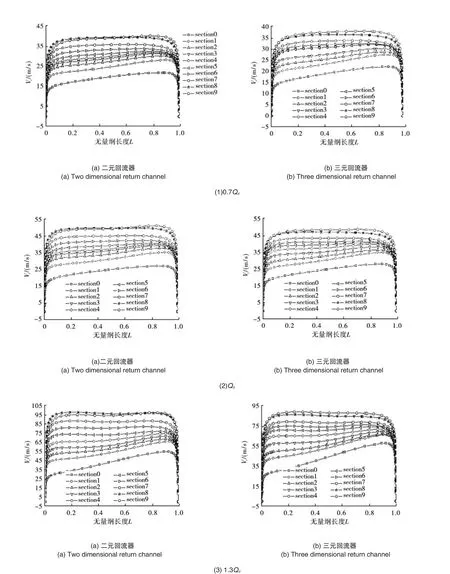
图9 变工况回流器内周向平均径向速度Vr沿叶高分布Fig.9 The circumferential averaged radial velocityVralong the distribution of blade height in the return channel in variable working condition

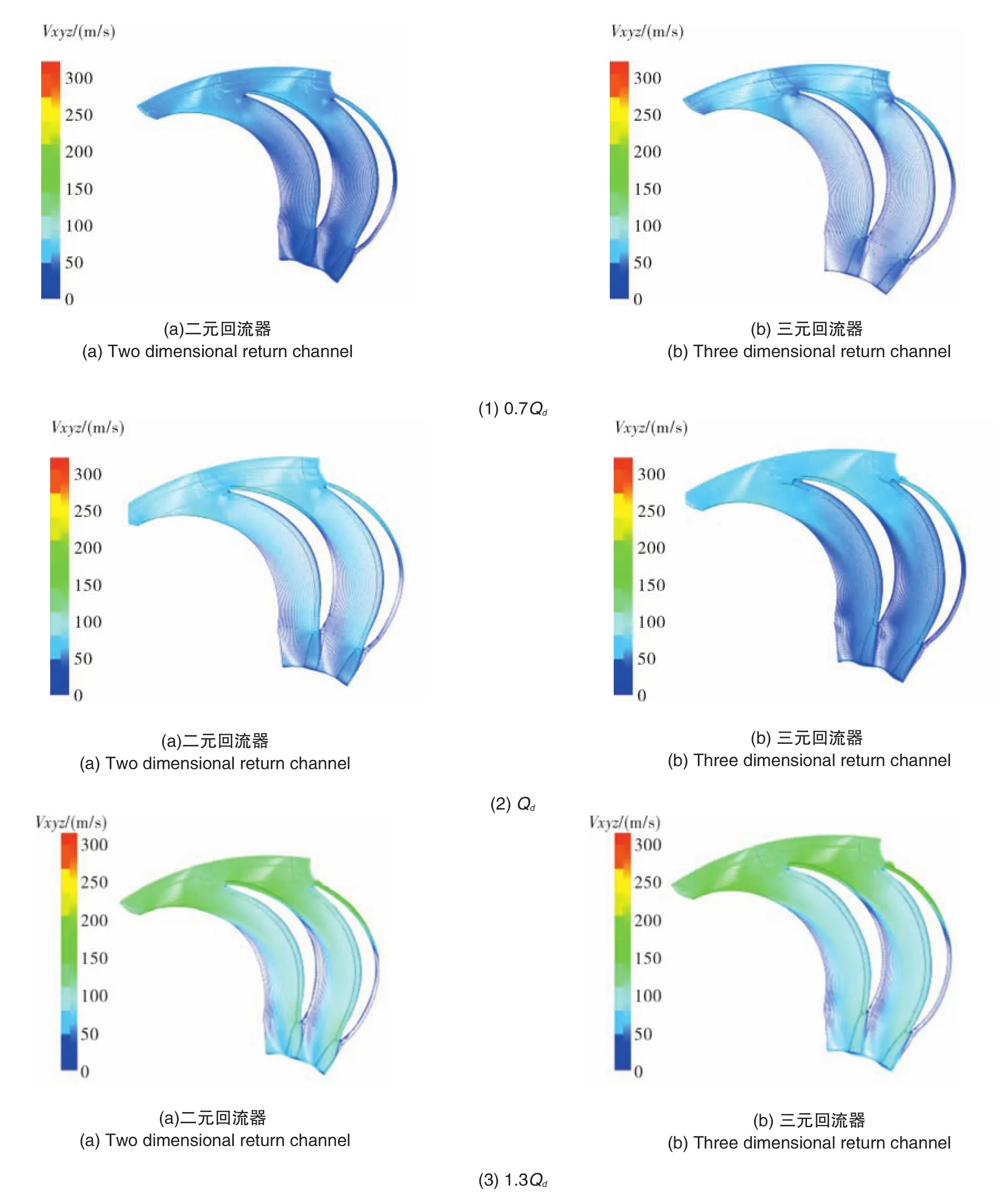
图10 回流器叶片半叶高截面速度矢量图Fig.10 Velocity vector of half blade height section of return channel blade

3 结论

使用将人工神经网络ANN、CFD技术以及遗传算法GA相结合的优化方法，对离心式压缩机基本级R回流器叶片上、下中型线、叶片厚度进行了优化设计，优化后叶型折转角β变大，径向产生正倾角；结果表明：这些变形特点有利于减少回流器流道内损失，提高静压恢复系数，并且改善了出口气流的均匀性，使得气体流动在回流器出口更加理想。此外，三元叶片回流器在整个工况范围内，静压恢复系数CP与二元回流器CP相比均有提高，在流量系数φ1为0.02时，静压恢复系数CP提高24.14%，级多变效率ηpol在流量系数φ1为0.026时多变效率提高了2.82%，在变工况下显著提高了整级性能。

[1] Veress A,Van den Braembussche R.Inverse Design and Optimization of a Return Channel for a Multistage Centrifugal Compressor[J].Journal of Fluids Engineering,2004,126(5):799-806.

[2]Reddy KS,Murty GVR,Dasgupta A,et al.Flow Investigations in the Crossover System of a Centrifugal Compressor Stage[J].International Journal of Fluid Machinery and Systems,2010,3(1):11-19.

[3]Aalburg C,Simpson A,Schmitz MB,et al.Design and Testing of Multistage Centrifugal Compressors with Small Diffusion Ratios[J].Journal of Turbomachinery-Transactions of ASME,2008,134(4):1667-1676.

[4]Glass BW.Improved Return Passages for Multistage Centrifugal Compressors[D].City of Cambridge,Massachusetts Institute of Technology,2010.

[5] HildebrandtA.Aerodynamic Optimisation ofaCentrifugal Compressor Return Channel and U-Turn with Genetic Algorithms[C].ASME Paper GT2011-45076,2011.

[6]Fakhri S,Sorokes JM,Vezier C,et al.Stationary Component Optimization and the Resultant Improvement in the Performance Characteristics of a Radial Compressor Stage[C].ASME Paper GT2013-95782,2013.

[7]鲁业明,刘正先.离心压气机弯道和回流器流道的优化设计[J].流体机械,2014,42(4):17-22.

[8]Strohmeyer H,Hildebrandt A.Aerodynamic Investigation on a 3DVaned Diffuser Applied on a High Flow 3D Impeller[C].ASME Paper GT2012-68327,2012.

[9]Abdelwahab A.The Aerodynamics of Three-dimensional Vaned Diffusers in Industrial Centrifugal Compressors[C].ASME Paper FEDSM2005-77333,2005.