动压径向滑动轴承油膜特性的数值计算∗
2018-03-21田奇勇黄文俊朱晓农王贤震
田奇勇 黄文俊 饶 杰 朱晓农 王贤震
(1.合肥通用机械研究院;2.安徽安风风机有限公司)
0 引言
流体动压滑动轴承承载能力强、运行平稳、抗振性好、寿命长,广泛应用于压缩机、汽轮机、离心机等设备。根据流体动压润滑理论,影响滑动轴承油膜压力分布的参数主要有轴承宽径比、相对间隙、径向载荷、润滑油工作温度和主轴转速等。传统的轴承参数计算方法是利用已有的宽径比的轴承静动态参数,首先假定平均工作温度,按所选润滑油确定粘度,并根据已知的轴承尺寸和运转参数,计算出轴承承载量系数,再结合轴承宽径比按已知的图表插值求得轴承工作状态下的各参数值,这种方法不太方便且有较大误差。
本文采用有限差分法对液体动压滑动轴承的静态参数进行计算,编制出通用性较强的实用计算程序,以代替传统的图表计算,缩短了设计周期,提高了设计效率,对流体动压滑动轴承的设计及故障诊断均具有较大帮助。
1 Reynolds基本方程
流体动压滑动轴承结构示意图见图1,二维稳态等温层流不可压缩流体Reynolds方程[6]:

式中,h为径向轴承油膜厚度;μ为润滑油工作温度下动力粘度;p为油膜压力;U为轴承处轴径线速度。
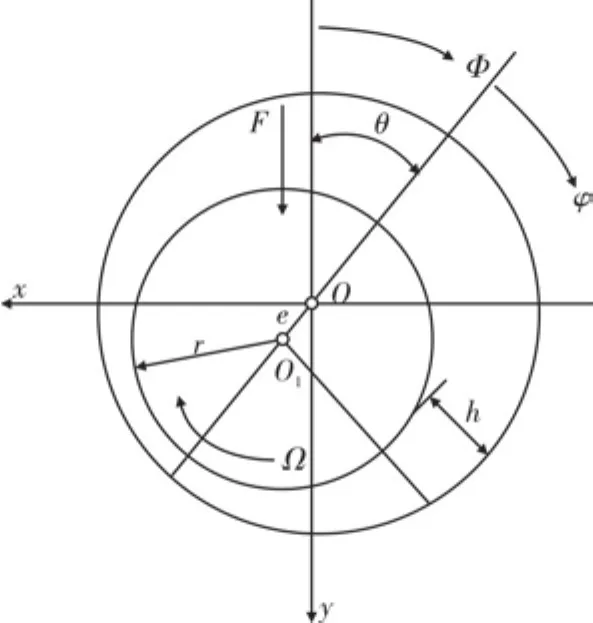
图1 动压轴承结构示意图Fig.1 Dynamic pressure bearing structure diagram
研究动压径向滑动轴承的关键问题就是对Reynolds方程进行求解,由于二维Reynolds方程的复杂性,一般都进行各种假设以将其简化。比较典型的是将轴承假设为无限宽或无限窄,此时方程转化成一维稳态流动雷诺方程,目前对这两种情况下的雷诺方程可以得到较为精确的解析解,对研究径向滑动轴承的各种性能有一定的指导意义,如这些解析解指出了轴承性能的趋向,而且确定了轴承性能的上限和下限,然而实际轴承是有限宽的,需求解完整的二维流动雷诺方程[7]。
为了便于计算机运算,将Reynolds方程无量纲化,取轴承处轴半径r作为“相对单位”来度量x,得φ=x r,φ为从竖直位置开始计算的轴承偏角,其取值范围根据具体轴瓦结构来确定;对轴向坐标z,选取轴承宽度L的一半作为相对单位,则z方向的无量纲坐标λ=z(L/2),坐标原点放在宽度中央,则λ的区间是-1≤λ≤1。无量纲油膜厚度H=h c=1+εcosφ,c为轴承半径间隙,ε为偏心率,则得到无量纲化形式为:

式中,D为轴径直径;p=p p0为无量纲化油膜压力,p0=2Ω μ ψ2;ψ为半径间隙比。
2 数值求解方法
2.1 差分法求解Reynolds方程原理
采用有限差分法将式(2)离散,将轴瓦的油膜划分为m×n个方格(m为圆周φ方向,n为宽度λ方向),将网格节点按所在列数和行数顺序编号,沿φ方向的列数用i编号,即从1到m+1;沿λ方向的行数用j编号,即从1到n+1;每个节点的位置用(i,j)二维编号表示,用各个节点上的压力值构成各阶差商,近似取代Reynolds方程中的导数,则近似方程为:
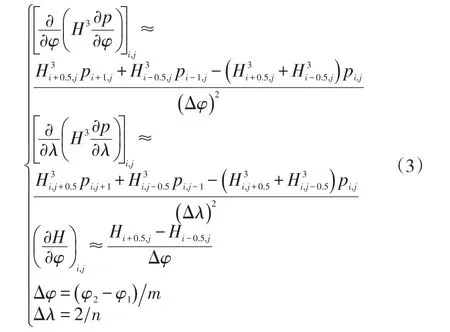
将式(3)差分表达式代入式(2)中得:
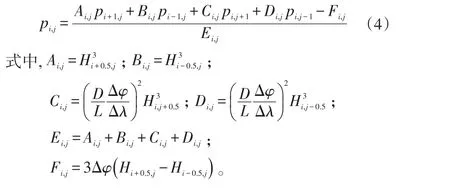
从式(3)和式(4)将Reynolds方程化为一组代数方程,根据(i,j)节点周围四节点上的压力值来计算中间节点的压力值,由此解出各节点上的压力值,得到一组离散的压力数值,近似表达出油膜中的压力分布,然后根据这组压力值,用相应的数值积分,求得轴承的承载力、阻力、流量、温升等静态性能值。
2.2 求解边界条件
求解Reynolds方程时,边界条件的处理对压力分布的影响很大,因此,边界条件的确定是一个十分重要的问题。常用的边界条件有Sommerfeld边界条件,半Sommerfeld边界条件和Reynolds边界条件,对于有限长动压轴承,公认Reynolds边界条件比较符合实际[5-7]。Reynolds边界条件认为油膜不连续,压力油膜的终点在最小油膜厚度后油楔发散区的某个位置φp处,该处油膜出现自然破裂,本文计算采用Reynolds边界条件。
2.3 程序化计算流程与分析
传统方法是利用已有的轴承宽径比下的静动态参数图表,首先假定轴承的工作平均温度,按所选润滑油确定油的粘度,并根据已知的轴承尺寸和运转参数,计算出轴承承载量系数,再由和轴承宽径比L D按已知的图表插值或拟合求得轴承工作状态下的各参数值,其目的在于核算工作状态下最小油膜厚度、功耗、供油量和温升等是否在容许范围内。这种插值或拟合会引入误差,影响结果的判断,给设计带来诸多不便。
本文编程计算流程见图2,直接利用已知的运转参数对外载荷进行迭代计算,避免了插值运算带来的误差,求解精度较高。

图2 计算流程图Fig.2 Calculation flow chart
3 算例及结果分析
以文献[6]第五章表5-4中宽径比L D=1.0的圆柱轴承和表5-5中L D=0.5及椭圆比为0.5的椭圆轴承为例。圆柱轴承各参数计算结果见表1,偏位角θ的最大偏差不超过0.30%,承载量系数的偏差最大不超过0.1%;椭圆轴承各参数计算结果见表2,偏位角θ的最大偏差不超过0.30%,承载量系数的偏差最大不超过0.6%。本文的计算结果与文献[6]的结果吻合良好,从而验证了本文所述方法的计算程序的精度较高。
文献[6]第五章例1(部分计算结果见表1),某机械用流体动压径向滑动轴承,轴承处载荷F=31 882.5N,转速n=3 600r/min,轴承公称直径D=152mm,宽径比L D=1.0,相对间隙ψ=0.002,润滑油工作粘度为18.006×10-3Pa·s。
表1 圆柱轴承各参数计算结果对比[6]Tab.1 The comparison of θandmcalculation results in cylindrical bearing
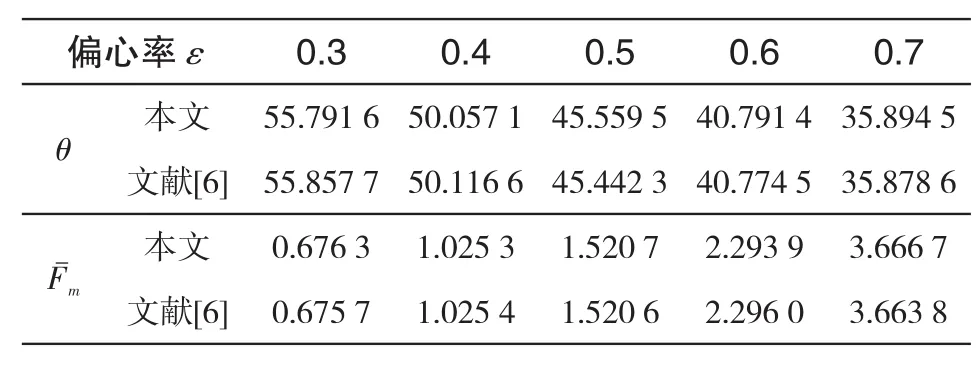
表1 圆柱轴承各参数计算结果对比[6]Tab.1 The comparison of θandmcalculation results in cylindrical bearing
偏心率ε θ>m本文文献[6]本文文献[6]0.3 55.791 6 55.857 7 0.676 3 0.675 7 0.4 50.057 1 50.116 6 1.025 3 1.025 4 0.5 45.559 5 45.442 3 1.520 7 1.520 6 0.6 40.791 4 40.774 5 2.293 9 2.296 0 0.7 35.894 5 35.878 6 3.666 7 3.663 8
表2 椭圆轴承各参数计算结果对比[6]Tab.2 The comparison of θandF>mcalculation results in elliptical bearing

表2 椭圆轴承各参数计算结果对比[6]Tab.2 The comparison of θandF>mcalculation results in elliptical bearing
偏心率ε θm本文文献[6]本文文献[6]0.3 89.630 5 89.850 4 0.072 7 0.073 1 0.4 88.585 7 88.580 9 0.105 0 0.105 6 0.5 87.070 1 87.023 9 0.146 3 0.145 5 0.6 84.601 3 84.683 3 0.201 1 0.202 3 0.7 81.551 9 81.232 1 0.285 6 0.286 6
按传统计算方法,根据已知条件计算出承载量系数=1.626,按表1插值计算得到轴承偏心率ε=0.513 7,偏位角θ=44.806 9°,然后再插值计算出其它性能参数,这样会带来插值计算误差。本文方法程序计算得到轴承偏心率ε=0.516 8,偏位角θ=44.778 6°,同时可获得最小油膜厚度、油膜破裂位置和摩擦功耗等参数。轴承下瓦无量纲油膜厚度和无量纲油膜压力分布分别见图3和图4所示。
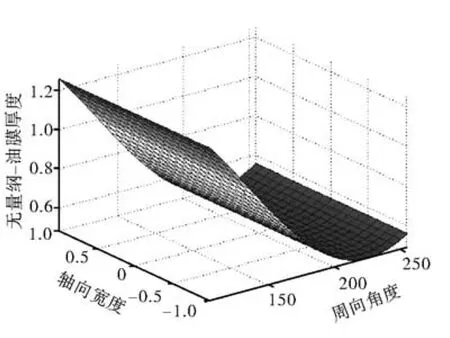
图3 圆柱轴承无量纲油膜厚度分布Fig.3 Non-dimensional of cylindrical bearing oil film thickness distribution

图4 圆柱轴承无量纲油膜压力分布Fig.4 Non-dimensionless oil film pressure distribution of cylindrical bearing
通过图4可知,沿周向无量纲油膜压力先增大后减小,在某一点达到最大值,并且呈非线性;沿宽度方向以中央最大呈抛物线状。当得到油膜压力后,可以通过对压力分布积分求得流量系数、阻力系数、摩擦功耗、油膜刚度和油膜阻尼系数等[8-10]。
4 结论
采用有限差分法求解二维Reynolds方程可以计算出轴承油膜厚度和油膜压力分布,同时可直接得到轴承偏心率、偏位角、最小油膜厚度、油膜破裂位置和摩擦阻力等参数,即采用数值计算可以方便、快捷地得到不同参数下轴承的各项性能值,且轴承参数可以任选,避免了计算传统方法中根据图表的插值或拟合所产生的误差。本方法的使用还可以较好地掌握轴承的实际工作状态,对实际设备的运行维护、轴承的选型设计有较强的指导意义。
[1]黄民毅.液体动压滑动轴承设计的数值计算[J].四川工业学院学报,1998,17(3):37-41.
[2]张祖立.液体动压径向滑动轴承静态特性参数的计算机程序设计与计算[J].沈阳农业大学学报,1999,30(4):440-443.
[3]孟繁娟,杜永平.径向滑动轴承油膜压力分析[J].轴承,2008(1):23-25.
[4]王增胜,穆国华,牛月兰,等.基于Matlab的动压轴承油膜特性仿真研究[J].机械,2013,40(2):9-10,23
[5]谢帆,荆建平,万召,等.基于有限差分法的径向滑动轴承油膜压力分布计算[J].润滑与密封,2012,37(2):12-15.
[6]西安交通大学透平压缩机教研室编著.离心式压缩机强度[M].北京:机械工业出版社,1980.
[7]敏政,王乐,魏志国,等.基于MATLAB技术的滑动轴承油膜压力分布的模拟[J].润滑与密封,2008,33(8):51-53.
[8]康宁,迟启明.基于N-S方程的径向滑动轴承油膜承载力的计算[J].润滑与密封,2010,35(10):10-11.
[9]李元生,敖良波,李磊,等.滑动轴承动力特性系数动态分析方法[J].机械工程学报,2010,46(21):48-53.
[10]李强,许伟伟,王振波,等.滑动轴承动力特性的数值计算方法[J].中国石油大学学报(自然科学版),2014,38(5):165-172.
