多重线性回归分析的核心内容与关键技术概述

2018-03-20胡良平军事医学科学院生物医学统计学咨询中心北京100850世界中医药学会联合会临床科研统计学专业委员会北京100029通信作者胡良平maillphu812sinacom

四川精神卫生 2018年1期

胡良平(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029 通信作者：胡良平，E-mail：lphu812@sina.com)

1 与多重线性回归分析有关的基本概念

1.1 何为多重线性回归分析

在生物医药学和临床研究中的很多场合下，需要考察因变量如何依赖多因素变化而变化的规律，例如文献[1-2]都涉及到这种需求。此时，所需要的统计分析方法泛称为“多重回归分析”，当因变量为“计量变量”时，常被称为“多重线性回归分析”。

多重线性回归分析就是要求算出相应模型中参数的估计值，对回归方程和参数进行假设检验；在这个过程中，还需要对自变量进行筛选和共线性诊断、对观测点进行异常点诊断，基于构建的多重线性回归模型并在给定的自变量取值条件下对因变量的取值进行预测。多重线性回归模型(对总体而言)与回归方程(对样本而言)的表达式分别见式(1)和式(2)。

设用Y代表因变量，X1、X2、…、Xm分别代表m个自变量，则多重线性回归模型可以表示为：

Y=β0+β1X1+β2X2+…+βmXm+ε

(1)

式中β0为总体截距，β1、β2、…、βm分别为各个自变量所对应的总体偏回归系数，ε为随机误差，常假定其服从正态分布。偏回归系数βi(i=1,2,…,m)表示在其他自变量固定不变的情况下，Xi每改变一个测量单位时所引起的因变量Y的平均改变量。多重线性回归模型的样本回归方程可以表示为：

(2)

在建立了回归方程以后，就可以对因变量与自变量之间的线性依存关系进行定量分析，进而还可以利用回归方程对因变量进行预测。

1.2 如何在进行多重线性回归分析前估计样本含量

在进行试验研究或调查研究之前，一般都需要估计所需的最低样本含量。在进行多重线性回归分析前，同样也需要估计样本含量。具体的方法可分两步走[3]：

第一步，估计简单直线回归或相关分析时所需要的样本含量。

设因变量为Y，自变量为X1；再设它们之间的简单相关系数ρ(≈r)，其中，ρ为两变量之间的总体相关系数，而r为两变量之间的样本相关系数。此时，所需要的样本含量n1见式(3)：

(3)

在式(3)中，α、β都表示标准正态分布曲线下两尾端面积之和；Zα/2=Z0.05/2=1.96为标准正态分布曲线下两尾端面积之和为0.05时对应的横坐标(也被称为临界值)，同理，可理解Zβ=Z0.1=1.28的含义；当总体相关系数ρ未知时，一般用样本相关系数r取代。

若在简单直线回归模型中新增加(m-1)个自变量，则为了检验X1的回归系数是否为0，此时，样本含量nm的计算公式见式(4)：

(4)

(5)

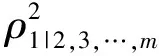
1.3 适合进行多重线性回归分析的数据结构

问题与数据结构见例1和表1。

【例1】26例糖尿病患者的血清总胆固醇(X1)、甘油三酯(X2)、空腹胰岛素(X3)、糖化血红蛋白(X4)、空腹血糖(Y)的测量值列于表1，建立血糖依赖其他几项指标变化的多重线性回归模型(说明：本例的研究者并没有事先估计所需要的样本含量)。

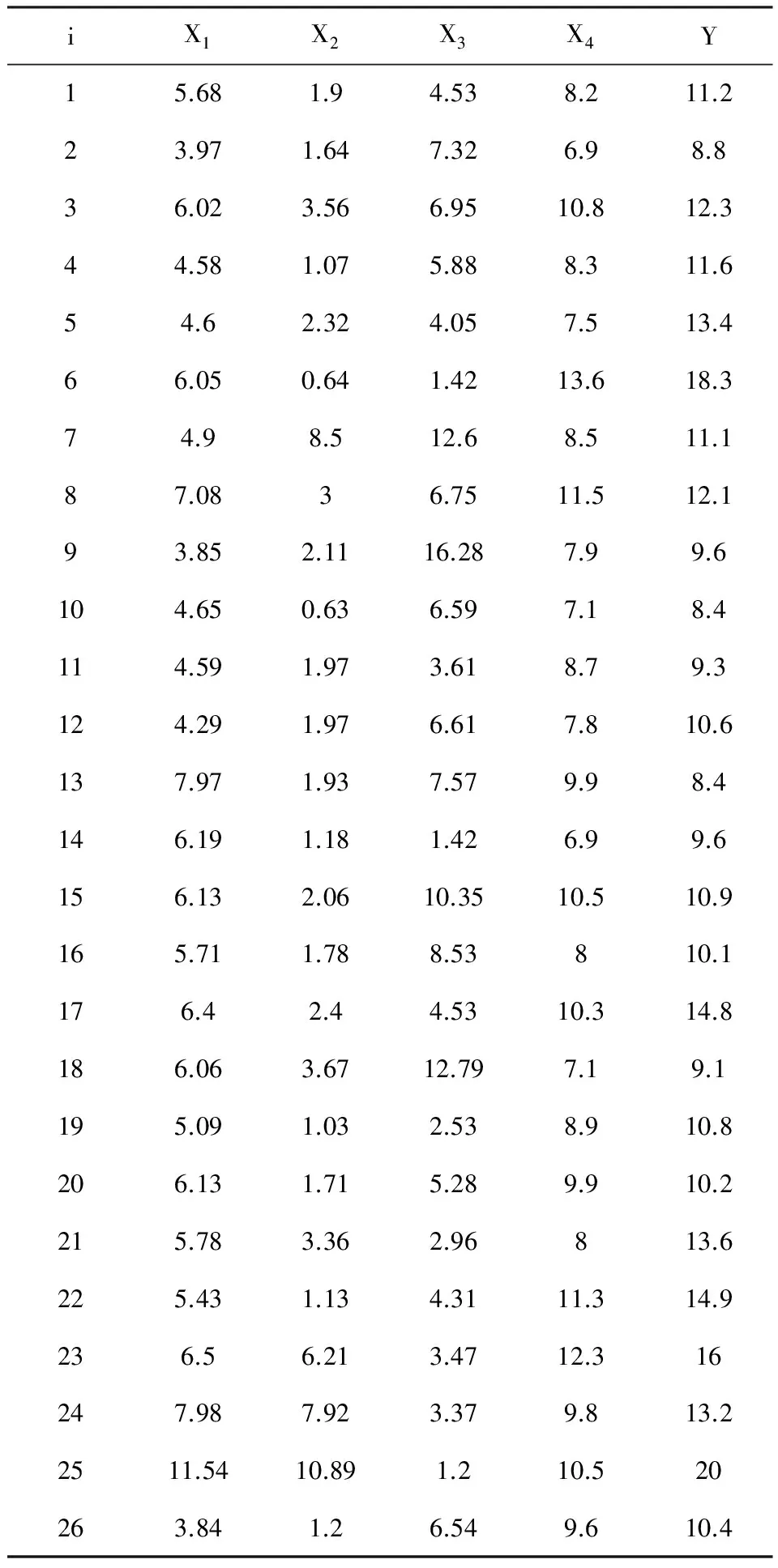
表1 26例糖尿病患者血样中有关指标的测定结果

【对数据结构的解说】在表1中，研究者从26例糖尿病患者体内抽血，对每份血样进行检查，测定了“血清总胆固醇(X1)、甘油三酯(X2)、空腹胰岛素(X3)、糖化血红蛋白(X4)、空腹血糖(Y)”5个定量变量的取值。它们之间的数量关系是客观存在的，而且是并存关系，不存在谁是自变量、谁是因变量。对资料进行统计分析时，可以有多种不同的统计分析目的，仅当希望分析“空腹血糖(Y)”是否随着“X1、X2、X3、X4”变化而变化时，才人为地将前者视为“因变量”、将后者视为“自变量”。

1.4 多重线性回归分析要求资料应满足的前提条件

结合上面的表1，呈现多重线性回归分析要求资料应满足的前提条件如下：

第一，受试对象具有同质性。受试对象为26例糖尿病患者，而不是患有其他疾病的患者，也不是正常人。这里还有一些隐含的前提条件未明确交代：所患糖尿病的类型、严重程度、病程、是否有糖尿病家族史等基本相同，年龄、性别、职业、身体素质、生活和饮食习惯、锻炼方式和程度等基本相同。

第二，全部变量、特别是因变量是计量变量。经典统计学中，要求进行多重线性回归分析的全部变量都是定量的；在具体使用时，条件有所放松，即自变量中允许有二值定性变量或多值有序变量，若有多值名义变量，需要将其变换为二值的“哑变量(其个数为原多值名义变量的水平数减一)”。

第三，各自变量组合条件下的计量因变量应服从正态分布且方差相等。这一条仅仅局限于“统计理论”上的规定或假定，在实际使用时是无法考证的。因为每个定量自变量的取值都有无穷多个，全部自变量的不同水平组合自然也就有无穷多种了。而在实际研究中，样本含量十分有限，几乎没有两个受试对象在全部自变量上的取值是完全相同的，那么，怎样考察第三个前提条件是否成立呢？故在实际使用中，只能大大降低要求：只要因变量的全部取值近似服从正态分布即可。

第四，因变量与全部自变量间存在线性关系，而非曲线关系。这一点可以通过绘制因变量与每一个自变量之间的散布图来初步了解。

第五，全部自变量间互相独立，不存在共线性关系。当所拟合的多重线性回归模型中确实存在多重共线性问题时，则此多重线性回归模型的质量就不高。所以，应先进行共线性诊断，当发现存在多重共线性时，要设法消除，然后再构建多重线性回归模型。

1.5 如何进行回归诊断

1.5.1 何为自变量间的多重共线性

所谓多重共线性，就是某几个自变量之间存在线性关系，例如：X1=0.35X2+1.28X3-21.45X4。

1.5.2 如何诊断自变量之间是否存在多重共线性

诊断是否存在多重共线性的方法有多种，如方差分量法、方差膨胀因子法(等价于容许度法)等，计算公式较复杂，此处从略；若借助SAS软件中的REG过程来拟合多重线性回归模型，只需在model语句中增加选择项“COLLIN”和“COLLINOINT”或“VIF”和“TOL”即可实现。

1.5.3 何为异常点以及如何诊断

若在回归分析的资料中，所有的观测点(表1中就有26个观测点)都是“同质的”，则不存在“异常点”；若有少数个体(即观测点)与其他绝大多数个体不同质，则它们就有可能成为异常点。为了便于直观理解异常点，参见图1。

图1 某实际问题中(x,y)的散布图

图1中，最右边的那个点在大多数点的延长线上且偏离得很远，这样的“异常点”可以通过“Cook’s D”统计量(其取值远远大于0.5就属于异常点)进行诊断；还有一个点在垂直于x轴的方向上偏离多数点较远，此类“异常点(在图1中偏离较小，暂时可将其视为可疑异常点)”可以通过“学生化残差”统计量(其取值的绝对值大于2时就可定为异常点)进行诊断。这两种统计量的计算公式此处从略。

1.6 筛选自变量和剔除异常点的意义和方法

1.6.1 筛选自变量的意义和方法

筛选自变量的意义在于：淘汰掉那些对因变量影响无统计学意义的自变量，使拟合的多重线性回归模型精简且具有更高的价值。在SAS软件包中，实现对自变量进行筛选的model语句的选项有以下8个[4]，即：

①selection=forward(采用前进法筛选自变量，变量经假设检验只进不出)；

②selection=backward(采用后退法筛选自变量，变量经假设检验只出不进)；

③selection=stepwise(采用逐步法筛选自变量，变量经假设检验有进有出)；

④selection=maxr(基于最大复相关系数的平方筛选自变量)；

⑤selection=minr(基于最小复相关系数的平方筛选自变量)；

⑥selection=rsquare(基于复相关系数的平方由大到小且所含自变量个数由少到多给自变量组合排序)；

⑦selection=adjrsq(基于校正的复相关系数的平方由大到小且所含自变量个数由少到多给自变量组合排序)；

⑧selection=cp(基于Mallow' sCP统计量的计算结果筛选自变量，此值越接近当前回归方程中自变量的个数，表明此时的回归方程质量越好)。

1.6.2 剔除异常点的意义和方法

若资料中确实存在严重的异常点，可能会导致所拟合的多重线性回归模型严重歪曲实际情况，很可能会得出误差很大的预测结果；若借助SAS软件中的REG过程来拟合多重线性回归模型，只需要在model语句中增加选择项“r”(即要求进行残差分析)就可实现。

2 构建多重线性回归分析模型方法

2.1 基于经典统计思想构建多重线性回归分析模型

构建多重线性回归分析模型的经典统计思想是：假定模型(1)中的误差项服从正态分布且各自变量组合条件下因变量Y的方差相等，在此假定成立的条件下，基于最小二乘原理构造一个偏差函数Q[5]，见式(6)：

(6)

为了使Q达到最小，由高等数学知识可知，将Q对b0、b1、b2、…、bm求一阶偏导数并且使之为0，就可以得到包含(m+1)个方程的正规方程组，然后利用求解线性方程组的方法就可由该正规方程组解得各个参数的估计值。为简便起见，下面以导出简单直线回归模型中参数估计值为例，呈现其推导过程：

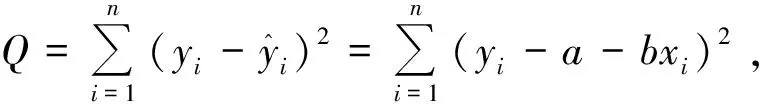
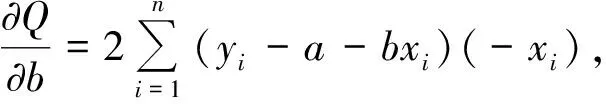
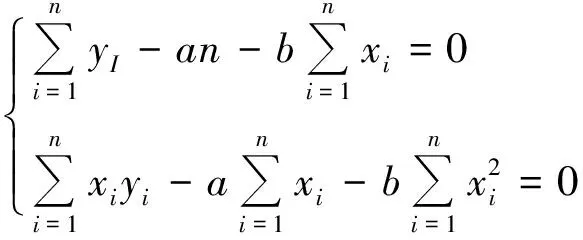
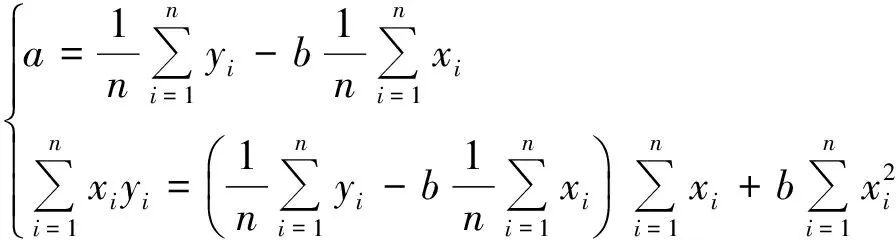
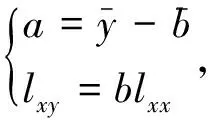
按以上程序确定直线回归方程中两个参数估计值，就被称为按最小二乘法或最小平方法进行参数估计。

2.2 基于贝叶斯统计思想构建多重线性回归分析模型

贝叶斯统计思想是充分利用并有效整合“样本信息、总体信息和先验信息”，再基于经典统计中的“概率分布知识”和蒙特卡罗统计思想中的“随机抽样”和“统计模拟”技术，构建所需要的多重线性回归模型，进而进行“共轭先验下的贝叶斯推断”和/或“广义先验下的贝叶斯推断”求出多重线性回归模型中的“估计回归系数矩阵”和“估计误差协方差矩阵”。这些内容的数学味过浓，感兴趣的读者参阅文献[6]，详细内容此处从略。

2.3 基于机器学习统计思想构建多重线性回归分析模型

机器学习的含义是希望通过对计算机编程，使它能够根据已有的输入数据进行学习[7]。这里所说的“学习”与人类为了了解未知事物或不会的知识时进行的“学习”是有区别的。在解决不同的问题时，这种学习需要“具体化”。例如，在进行简单直线回归分析时，若基于经典统计思想，前面介绍了依据最小二乘原理可以直接推导出直线回归方程中两个参数估计值的计算公式(7)，而利用机器学习方法却无法给出公式(7)。若基于机器学习统计思想，其解决问题的思路如下[8]：

将拟分析的资料随机划分成两部分，分别称为“训练集”与“测试集”，设其样本含量分别为n与k。让计算机在训练集上进行学习，在测试集上设法使均方误差[见式(8)]达到最小值，此时，所得的结果就是“机器学习的结果”(相当于得到了回归模型)。然后，将“机器学习的结果”用于测试集，即把测试集中自变量的数值代入已创建的回归模型求出因变量的估计值，再求出测试集上因变量的残差平方和，进而求出均方误差，见式(9)。

(8)

(9)

在上述的计算过程中，用机器学习法实现回归分析时希望达到的最终目的是使式(9)取得最小值，但在具体实施时，却是基于使式(8)达到最小值这个目标来不断优化或改进回归模型[见式(10)]中的权重w来实现的。

(10)

在式(10)中，w∈Rn是参数向量。

值得一提的是：在经典统计思想中，求一个函数的最小值或最大值通常都是基于高等数学中求极值的方法来实现的；而在机器学习统计思想中，是通过事先给定的最小值的“阈值”来实现的。例如，要求式(8)或式(9)小于阈值“10-4”。显然，阈值越小，迭代计算的次数就会越多。有时阈值定得过小，无论迭代计算多少次都难以满足要求，此时可能就会出现所谓不能收敛的情形了。

3 多重线性回归分析模型的假设检验

3.1 对多重线性回归模型进行整体检验

在估计出回归模型的参数以后，需要对回归方程进行显著性检验，检验的原假设为：

H0：β1=β2=…=βm=0

(11)

该假设表示所有的偏回归系数都为0，也就是全部自变量对因变量的作用都没有统计学意义，相应的备择假设为偏回归系数不全为0。检验的方法是方差分析，其基本思想与简单线性回归相同，将总的离均差平方和分解为回归平方和与残差平方和，然后构造F统计量，F统计量分子与分母的自由度分别为νR=m、νE=n-m-1。其计算公式为：

(12)

式中MSR与MSE分别称为回归均方和残差均方。求出F值后查F界值表，如果得到的P值小于事先确定的显著性水平，就说明回归方程有统计学意义。