基于经典统计思想实现多重线性回归分析

谷恒明，胡良平,2(.军事医学科学院生物医学统计学咨询中心，北京 00850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 00029 通信作者：胡良平，E-mail：lphu82@sina.com)

1 基于三种统计思想建立多重线性回归模型的概述[1-3]

1.1 经典多重线性回归分析建模概述

多重线性回归分析是用回归方程定量地刻画一个因变量与多个自变量之间的线性依存关系。其中，因变量是连续型变量，自变量是相互独立的连续型变量(也常包括少量分类变量)。

经典多重线性回归分析的内容包括对自变量的筛选和回归诊断(含多重共线性诊断和异常点诊断)、对回归模型和模型中全部参数的假设检验、对模型拟合效果的评价以及利用求得的回归模型对因变量进行预测。

对自变量的筛选有八种方法：①前进法；②后退法；③逐步法；④最大R2增量法；⑤最小R2增量法；⑥R2选择法；⑦修正R2选择法；⑧Mallow’s Cp统计量选择法。

当自变量之间存在较多的、严重的多重共线性关系时，通常可采用岭回归分析或者主成分回归分析。

设用Y代表因变量，X1、X2、……、Xm分别代表m个自变量，则多重线性回归模型可表示为：

Y=β0+β1X1+β2X2+…+βmXm+ε

(1)

式中β0为总体截距，β1、β2、…、βm分别为各个自变量所对应的总体偏回归系数，ε为随机误差。偏回归系数βi(i=1,2,…,m)表示在其他自变量固定不变的条件下，Xi每改变一个测量单位时所引起的因变量Y的平均改变量。多重线性回归模型的样本回归方程可以表示为：

(2)

1.2 贝叶斯回归分析建模概述

Yi=μi+εi,εi～N(0,σ2),i=1,2,…,n,

μi=β0+βiXi,

(3)

这里要为各个参数指定一个先验分布，例如：

π(β0)=φ(0,var=le6)

π(β1)=φ(0,var=le6)

π(σ2)=fiΓ(shape=3/10,scale=10/3)

(4)

经典多重线性回归分析假定自变量前的回归系数是固定的，而贝叶斯回归分析认为参数是随机的。基于贝叶斯统计思想建立回归模型时，要为各个自变量前的参数(即回归系数)和残差指定一个先验分布。可以依靠经验或预试验的结果指定各自合适的先验分布；如果没有办法给定先验分布，可以使用无信息先验(相当于均匀分布)代替。贝叶斯回归分析中没有自变量筛选功能，因此要借助经典多重线性回归分析中筛选方法筛选出来的自变量来建立回归模型。

贝叶斯统计建模可以参考SAS软件的STAT模块中MCMC过程来实现。MCMC方法即马氏链蒙特卡罗方法，默认算法是使用正态分布随机游动Metropolis算法。MCMC的抽样方法有Gibbs抽样、Metropolis抽样、独立性抽样、随机游动Metropolis抽样等[2]。

1.3 机器学习回归分析建模概述

有别于经典统计思想和贝叶斯统计思想，机器学习统计思想则另辟蹊径，它不依赖于概率分布知识、也不依赖于先验分布知识，而是通过基于训练样本的学习获取知识和经验，再用测试样本来验证。属于机器学习的具体方法很多，通常包括决策树法、支持向量机法、神经网络法、随机森林法和集成学习法等[3]。

1.4 三类方法回归建模效果

1.4.1 三类回归建模效果的评价

情形一，样本量较少时：分别使用两种方法建立回归模型，用相对误差绝对值的均值(abserror)，残差平方和(SSress)与决定系数(R2)作为评价指标。

情形二，样本量较多时：①全部数据用来建立模型并比较，评价指标同样本量较少时。②K-Fold交叉验证，即全部数据拆分为K份，其中(K-1)份用作建立模型的训练集，剩下一份当做测试集。训练集拟合效果使用相对误差绝对值的均值(abserror)，残差均方(MSE)与决定系数(R2)作为评价指标；测试集使用相对误差绝对值的均值(abserror)，残差均方(MSE)与标准化均方误差(NMSE)作为评价指标。③K-Fold交叉验证中，K取值分别为10、7、4和2。当K取定一个数值后，分别重复抽取10次，即进行10次重复建模。

1.4.2 评价指标的具体公式

(5)

在数值上，NMSE等于1-R2，这里的R2是回归的决定系数，但是，对于测试集来说，其NMSE与测试集回归的R2没有什么关系。交叉验证主要关心测试集的NMSE。

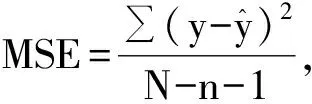
(6)

N为样本量，n为自变量个数。从上述的公式中可以看出，残差均方MSE是残差平方和与自由度的比值。交叉验证中K取值不同，建立模型的训练集和预测使用的测试集样本量是不同的，直接基于残差平方和比较不够合理，因此，需要除以自由度。

说明：BP 神经网络建模效果的评价指标采用公式(5)。

2 实例及基于经典统计思想的回归分析

2.1 问题与数据

【例1】26例糖尿病患者的血清总胆固醇(X1)、甘油三酯(X2)、空腹胰岛素(X3)、糖化血红蛋白(X4)、空腹血糖(Y)的测量值列于表1，试基于经典统计思想建立血糖与其他几项指标间的多重线性回归方程，并完成其他有关的任务。

2.2 回归分析任务

对例1表1中的数据，设因变量为Y，自变量为X1、X2、X3、X4，试建立因变量依赖自变量的多重线性回归模型，并做相应的假设检验。

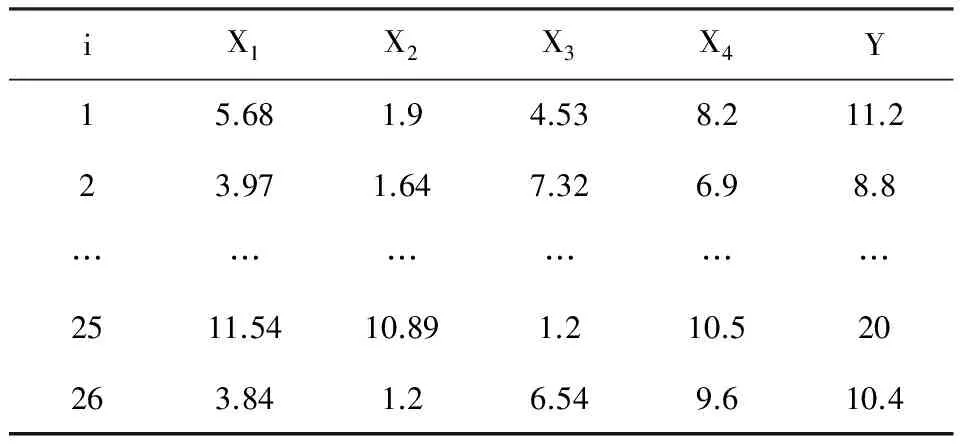
表1 26例糖尿病患者血样中有关指标的测定结果

注：详细数据见本期第一篇文章《多重线性回归分析的核心内容与关键技术概述》

2.3 采用经典统计思想实现多重线性回归分析的方法

(1)不产生派生变量并采用三种筛选自变量的方法建模

data cra1;

input id x1-x4 y @@;

cards;

……

;

run;

proc reg data=cra1;

model y=x1-x4/selection=stepwise sle=0.5 sls=0.05;

run;

proc reg data=cra1;

model y=x1-x4/selection=forward sle=0.05;

run;

proc reg data=cra1;

model y=x1-x4/selection=backward sls=0.05;

run;

【程序说明】“cards”语句后的省略号代表表1中26行6列数据，其中，第1列为“编号”；REG过程被调用了3次，分别采用逐步法、前进法和后退法筛选自变量；“sle=0.5”代表选变量进入回归模型的显著性水平，其概率值选用0.5是非常大的，以便有较多的变量有机会进入回归模型与其他变量进行组合，可以较好地保证单个作用不大但与某些自变量同时存在时作用明显增大的自变量不会被排斥在回归模型之外，这叫做“宽进”；“sls=0.05”代表已进入回归模型的自变量仍能被保留在回归模型之中的显著性水平，其概率值选用0.05是统计学上被公认的显著性水平，这叫做“严出”。

【主要输出结果】本例资料采用上述三种筛选自变量方法所得结果完全相同，其主要结果如下：

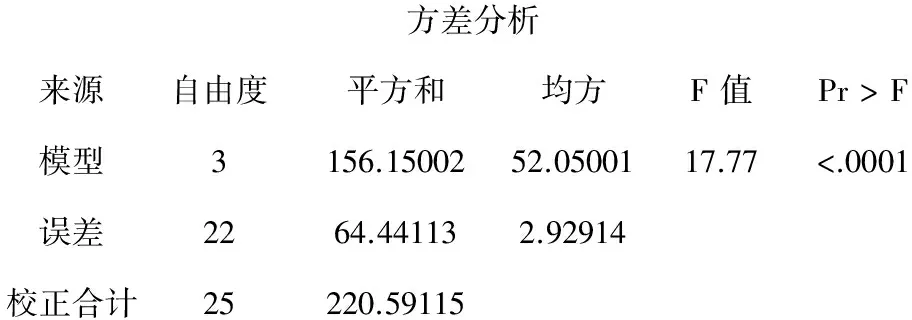
方差分析来源自由度平方和均方F值Pr>F模型3156．1500252．0500117．77<．0001误差2264．441132．92914校正合计25220．59115

变量参数估计值标准误差II型SSF值Pr>FIntercept4．914802．1491915．318005．230．0322x20．437960．1342531．1716810．640．0036x3-0．299490．0969927．927119．530．0054x40．812670．2062445．4791815．530．0007

【输出结果解释】第1部分表明：总的回归模型具有统计学意义(F=17.77、P<0.0001)；第2部分表明：自变量X1被淘汰掉了，其他3个自变量以及截距项均有统计学意义，得到的多重线性回归方程为：

(2)不产生派生变量并采用逐步法筛选自变量且进行共线性诊断和残差分析等方法建模

上面的SAS程序中的数据步程序不变，删除第2个和第3个过程步程序，第1个过程步程序修改如下：

proc reg data=cra1;

model y= x1-x4/selection=stepwise sle=0.5

sls=0.05 collin collinoint vif tol r stb;

run;

【程序说明】“collin”选项是要求系统给出采用“方差比例”算法且未校正回归模型中截距项影响的多重共线性诊断的结果；“collinoint”与前面选项的区别在于“校正了回归模型中截距项影响”；“vif”选项是要求系统给出采用“方差膨胀因子”算法的多重共线性诊断的结果、“tol”等于“1/vif”，即要求系统给出采用“容许度”算法的多重共线性诊断的结果；“r”要求系统给出“残差分析”的计算结果，有助于发现是否存在异常点；“stb”要求系统给出“标准化回归系数”的计算结果。

【主要输出结果及其解释】逐步回归分析的主要结果同上，此处从略。基于4种方法进行共线性诊断的结果如下：

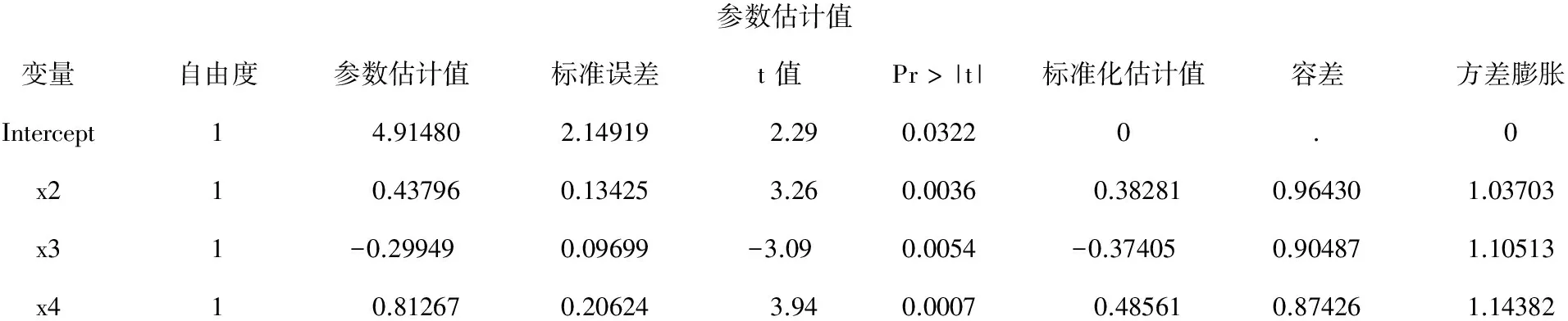
参数估计值变量自由度参数估计值标准误差t值Pr>|t|标准化估计值容差方差膨胀Intercept14．914802．149192．290．03220．0x210．437960．134253．260．00360．382810．964301．03703x31-0．299490．09699-3．090．0054-0．374050．904871．10513x410．812670．206243．940．00070．485610．874261．14382

以上为第1部分输出结果：倒数第3列为“标准化回归系数”，其绝对值越大，表明所对应的自变量对因变量的贡献就越大，由大到小依次为X4>X2>X3；倒数第2列和第1列分别为“容许度”与“方差膨胀因子”方法诊断共线性的结果，只需要看vif的数值是否大于10，大于10的那些行上的自变量间存在较严重的共线性。结果表明：3个自变量间不存在共线性关系。

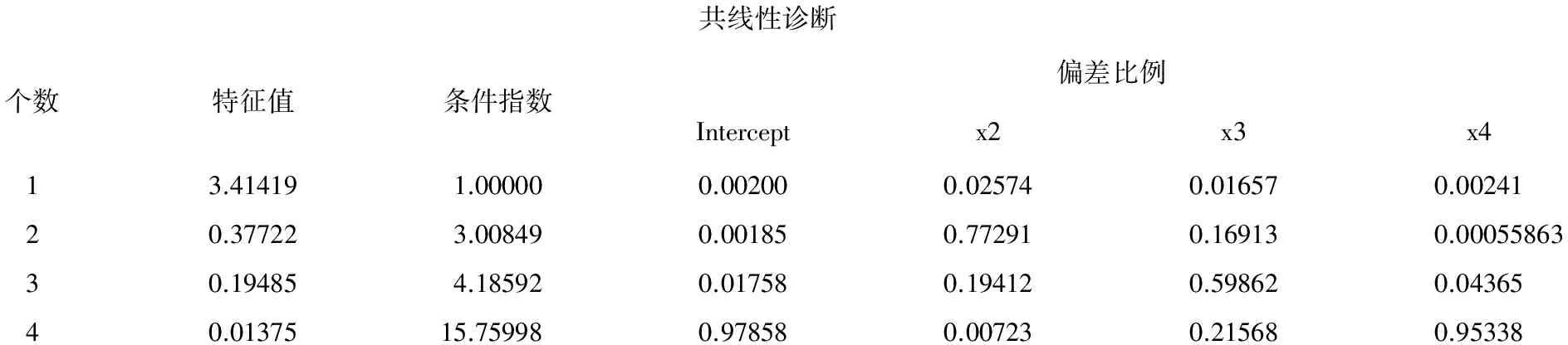
共线性诊断个数特征值条件指数偏差比例Interceptx2x3x413．414191．000000．002000．025740．016570．0024120．377223．008490．001850．772910．169130．0005586330．194854．185920．017580．194120．598620．0436540．0137515．759980．978580．007230．215680．95338

以上为第2部分输出结果：这是未对截距项进行校正且依据“方差比例”算法进行共线性诊断的结果。适用于“回归分析模型中截距项无统计学意义”的场合，而本例截距项有统计学意义，故不需要看这部分输出结果。

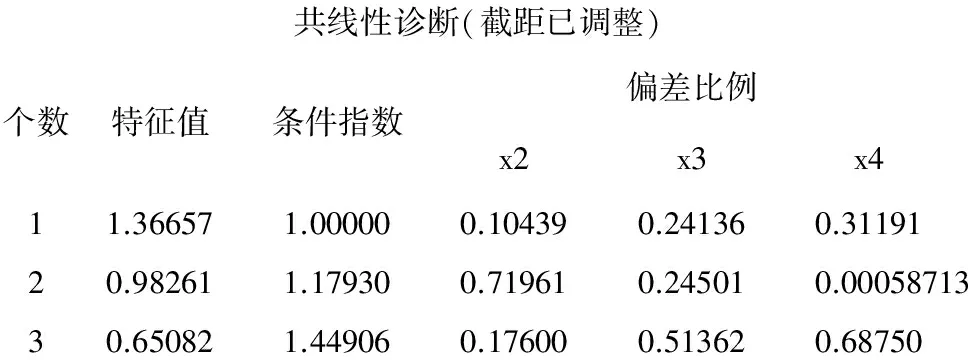
共线性诊断(截距已调整)个数特征值条件指数偏差比例x2x3x411．366571．000000．104390．241360．3119120．982611．179300．719610．245010．0005871330．650821．449060．176000．513620．68750

以上为第3部分输出结果：这是对截距项进行校正后且依据“方差比例”算法进行共线性诊断的结果。适用于“回归分析模型中截距项有统计学意义”的场合，而本例，截距项有统计学意义，故应该看这部分输出结果。评判是否存在共线性的方法：看3个自变量列输出结果的最后一行，当这些数值中有两个或多个数值都很大且接近于1，那么，它们对应的自变量间存在共线性。本例3个自变量间不存在共线性关系。

残差分析的输出结果很多，此处从略。从学生化残差结果来看，没有取值的绝对值大于2的观测点；从“Cook' s D”统计量计算结果来看，仅第25个观测点的取值为0.698大于0.5，表明此观测点是“可疑的异常点”。

(3)产生派生变量并采用三种筛选自变量的方法建模

所谓产生派生变量，就是除资料中已有的4个自变量外，再通过变量变换的方法，引入“新变量”。通常可以引入自变量的二次项，包括各自变量的平方项和任何两个自变量的交叉乘积项。在上面第1段SAS程序基础上，进行如下修改即可：

data cra2;

set cra1;

z1=x1*x1;z2=x2*x2;z3=x3*x3;z4=x4*x4;

z5=x1*x2;z6=x1*x3;z7=x1*x4;z8=x2*x3;

z9=x2*x4;z10=x3*x4;

run;

proc reg data=cra2;

model y=x1-x4 z1-z10/selection=stepwise sle=0.5sls=0.05;

run;

proc reg data=cra2;

model y=x1-x4 z1-z10/selection=forward sle=0.05;

run;

proc reg data=cra2;

model y=x1-x4 z1-z10/selection=backward sls=0.05;

run;

【程序说明】在已经运行原先SAS程序的基础上(即已经创建了SAS数据集cra1)，再创建新数据集cra2，这就是前两个语句的作用。新数据集中增加了z1-z10共10个新变量，它们是由原先的4个自变量产生的派生变量，代表10个二次项；3个过程步分别采用“逐步法”“前进法”和“后退法”筛选自变量，现在的自变量个数为14个。

以下是“逐步法”和“前进法”筛选自变量的结果：

方差分析来源自由度平方和均方F值Pr>F模型3163．1870154．3956720．85<0．0001误差2257．404142．60928校正合计25220．59115

变量参数估计值标准误差II型SSF值Pr>FIntercept6．633831．4014958．4617622．410．0001x30．728440．2845917．094866．550．0179z6-0．185080．0514233．7988912．950．0016z70．126960．02044100．6624738．58<0．0001

以下是“后退法”筛选自变量的结果：

方差分析来源自由度平方和均方F值Pr>F模型3172．9698357．6566126．64<0．0001误差2247．621322．16461校正合计25220．59115

变量参数估计值标准误差II型SSF值Pr>FIntercept8．669291．02421155．0855471．65<0．0001z40．045470．0087458．5510627．05<0．0001z50．051790．0117042．3827619．580．0002z6-0．054800．0156726．4665612．230．0020

考察以上两个不同的建模结果可以发现：后退法的建模结果稍好一些，因为其总模型的假设检验结果的F=26.64较大(较小者为F=20.85)且模型中所含的项数相同(均为4项)，总模型和各项假设检验结果均具有统计学意义。

结合前面未引入派生变量时得到的多重线性回归模型，其总模型的F=17.77，小于现在获得的最好的模型对应的F=26.64，故拟合本例资料最好的多重线性回归方程如下：

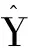
(4)产生派生变量并采用后退法筛选自变量且进行共线性诊断和残差分析等方法建模

在运行了前面第1个数据步程序(创建数据集cra1)和第2个数据步程序(创建数据集cra2)的基础上，再运行下面的过程步程序：

proc reg data=cra2;

model y= X1-X4 Z1-Z10/selection=backward

sls=0.05 collin collinoint vif tol r stb;

run;

输出结果较多，此处从略。结果表明：Z4、Z5、Z6三个项之间不存在共线性关系；残差分析的结果与前面陈述的结果基本相同，但第25个观测点对应的Cook' s D=0.441<0.5，说明它已经不属于“可疑异常点”了。

3 小 结

本文介绍了基于经典统计思想构建多重线性回归模型的主要内容，此法可用于很多多因素临床试验研究和观察性研究中，其主要的应用条件是结果变量为“计量变量”，例如主要评价指标为“评分”。值得注意的是：许多实际工作者在对此类资料进行统计分析时，喜欢选用单因素差异性分析，见文献[4-7]。其实，选用多重线性回归分析方法来实现多因素分析，效果更佳。

虽然，在本文中所介绍的实例中，自变量都是计量变量，而在实际使用中，自变量可以是计量的、计数的、定性的。但是，当自变量为多值名义变量时，需要产生哑变量后才能引入多重线性回归模型之中[8]，否则，可能得出错误的结论。

[1] Kleinbaum DG, Kupper LL, Muller KE, et al. Applied regression analysis and other multivariable methods[M]. 3版.北京: 机械工业出版社, 2003: 111-159.

[2] 刘金山, 夏强. 基于MCMC算法的贝叶斯统计方法[M]. 北京: 科学出版社, 2017: 118-174.

[3] 吴喜之. 复杂数据统计方法——基于R的应用[M]. 3版. 北京: 中国人民大学出版社, 2015: 41-56.

[4] 任传波, 姜季妍, 董黎明. 青少年抑郁障碍患者心理社会学特征[J]. 四川精神卫生, 2017, 30(5): 455-457.

[5] 徐华丽, 孙崇勇, 高悦. 大学生人格特质对手机成瘾倾向的影响[J]. 四川精神卫生, 2017, 30(5): 458-462.

[6] 李青青, 张倩. 医学院校大学生情绪状态与学业拖延的关系[J]. 四川精神卫生, 2017, 30(5): 463-465.

[7] 魏国英, 曾丽娟, 周桂成, 等. 精神科护士职业倦怠与工作压力的相关性[J]. 四川精神卫生, 2017, 30(5): 466-469.

[8] 胡良平. 医学统计学——运用三型理论进行现代回归分析[M]. 北京: 人民军医出版社, 2010: 9-33.