正态概率纸检验的改进及推广
2018-03-20王丙参魏艳华丁恒飞
王丙参,魏艳华,丁恒飞
(天水师范学院 数学与统计学院,甘肃 天水 741001)
一、引 言
正态分布应用广泛,比如许多统计方法(如方差分析、回归分析等)都是以正态分布为前提建立的[1]17-50[2]118-150[3-4]。因此,对数据进行正态性检验在理论和应用上都十分有意义。正态概率纸检验通过数据变换能使正态总体的取值x和分布函数值F(x)组成的数对(x,F(x))在具有特殊刻度的坐标纸上呈现一条直线,从而通过观察概率纸上的散点是否在一条直线附近来判断数据是否来自正态总体。因此,正态概率纸检验是一种直观、简单、方便的图形检验,特别适合于工程应用,但是,它具有一定的主观性,不太严。正态概率纸检验历史悠久,学者主要将其作为其他正态检验方法的定性补充[1]17-50[5]258-270,曹晋华等根据正态概率纸检的基本思想将其推广到威布尔分布、对数正态分布,但它们也是定性观察,没有量化[6]400-430。朱力行与许王莉等给出数据近似呈现一条直线可通过相关系数进行量化[7]1-26,孟杰与王佐仁等根据蒙特卡洛方法仿真目标分布,得到感兴趣的量,这为“概率纸上的散点在一条直线附近”进行量化提供了方法[3,4]。签于此,本文利用蒙特卡洛方法在正态概率纸检验中引入相关系数等指标,将定性与定量判断相结合,使得检验结果更加客观,最后将此方法推广到了对数正态分布、指数分布、威布尔分布。
二、正态概率纸检验及改进
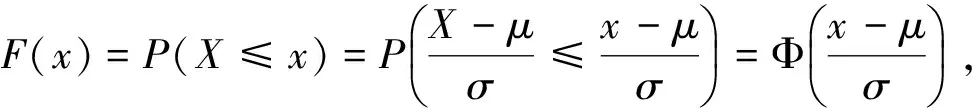
如果样本x1,x2,…,xn的次序统计量记为x(1)≤x(2)≤…≤x(n),则样本的经验分布函数就是:
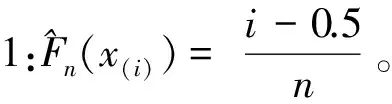
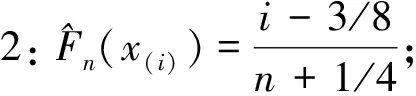
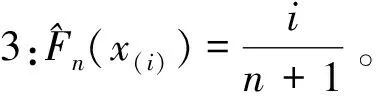
国标GB/T 4882-2001建议使用修正2,但也不反对使用其它两个修正。随着样本容量的增大,3种修正方法的区别也越来越小,且无法从理论上证明哪种修正严格更优。进一步有:
i=1,2,…,n。
显然,概率纸检验具有很大的主观性。为了克服概率纸检验的主观性缺点,可作以下改进:首先将观测数据进行标准化的排序处理并标在概率纸上,然后计算标准化数据的简单相关系数
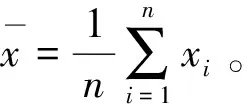
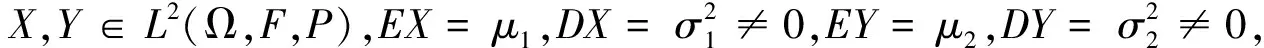
‖Y*-aX*-b‖=E(Y*-aX*-b)2
=1+a2-2aρ+b2
=(a-ρ2)+b2+1-ρ2
其中,ρ是X*、Y*的相关系数。显然,当a=ρ,b=0时,‖Y*-aX*-b‖最小,值为1-ρ2。这说明:Y*关于X*的最佳线性预测为h(X*)=ρX*,|ρ|越大,预测效果越好。当|ρ|=1时,Y*可以由X*完全准确的线性预测。因此,相关系数也称为线性相关系数。
假定n个观测数据x1,x2,…,xn来自总体F(x),先将观测数据进行标准化的排序处理,然后求得n个观测数据在概率纸上对应散点的简单相关系数为r0。考虑以下假设检验问题:
H0∶F(x)=F0(x);
H1∶F(x)≠F0(x),其中F0(x)为正态分布。
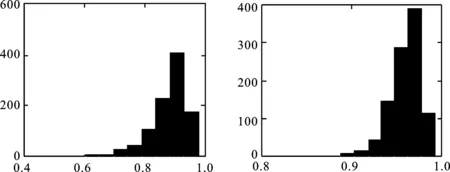
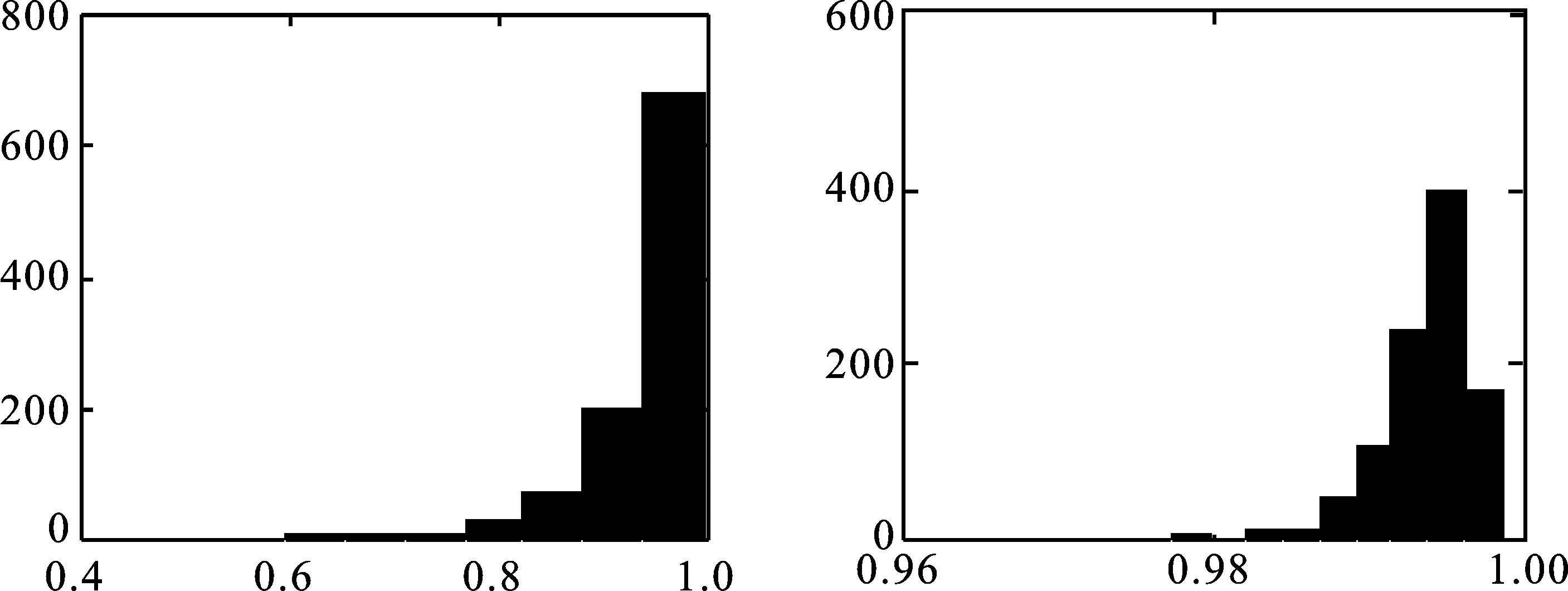
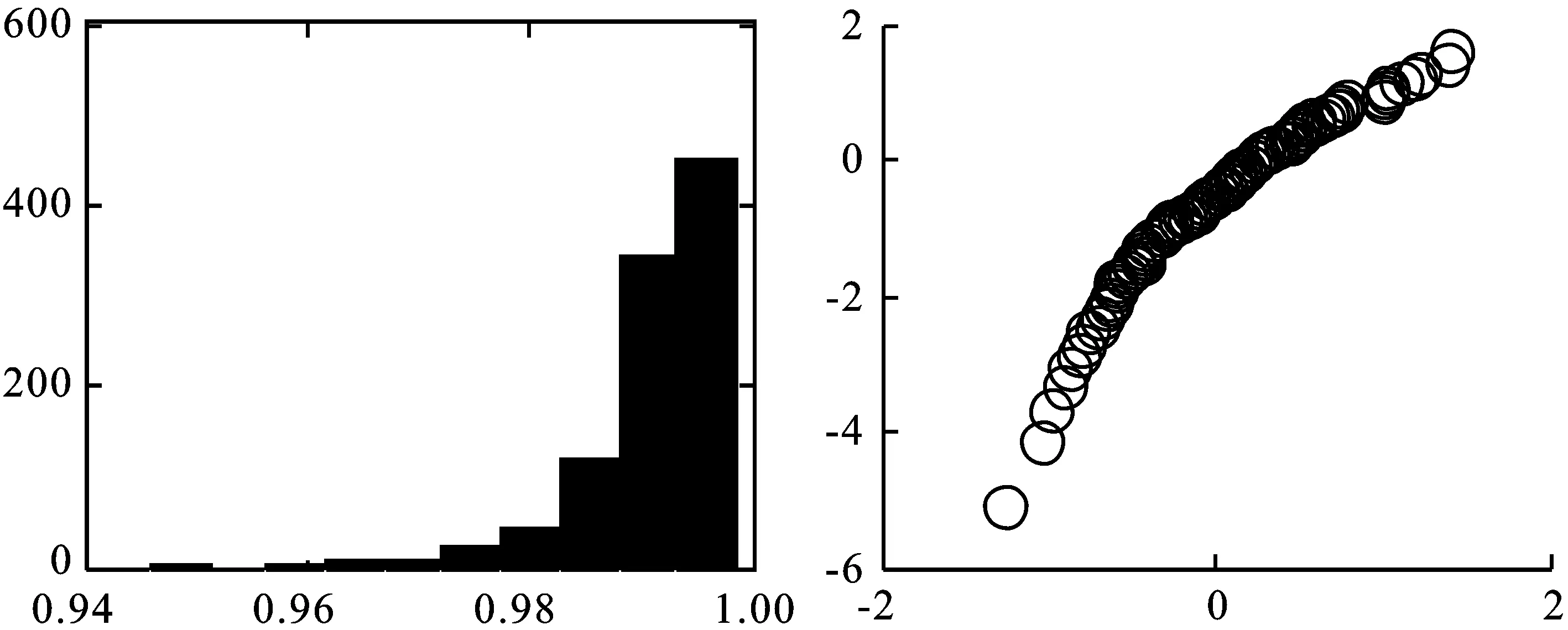
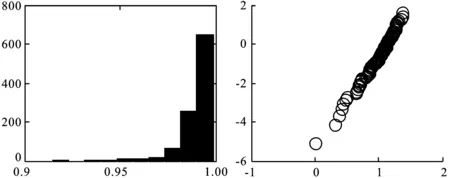
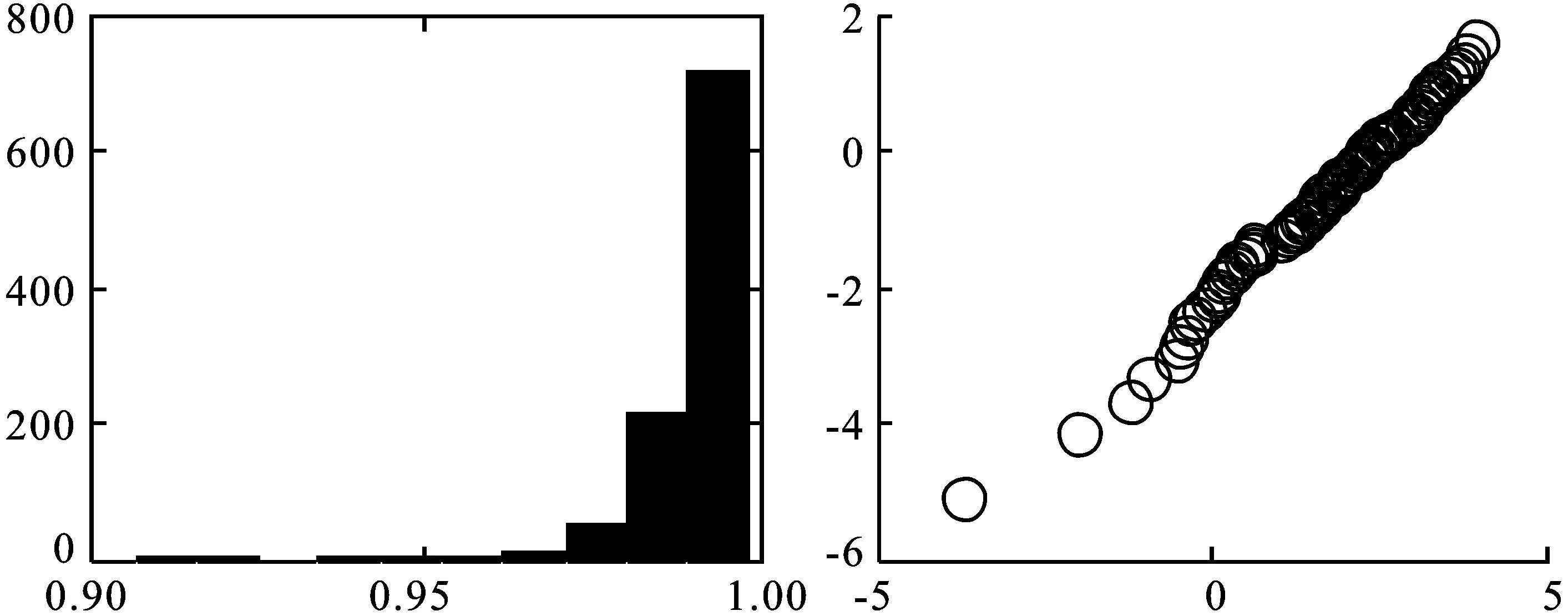
生成n个标准正态分布随机数,并计算这些随机数在概率纸上对应散点的简单相关系数,一共重复m次,相关系数分别记为r1,r2,…,rm。对于给定的显著性水平α,计算相关系数r1,r2,…,rm的α分位数,并记为rα(m)。将r0与rα(m)进行比较,如果观测数据的简单相关系数r0≥rα(m),则不能拒绝原假设(在二者差距较大时也可认为接受原假设),即不能拒绝观测数据来自正态总体F0(x);如果r0 下面对改进的正态概率纸检验进行蒙特卡洛分析。 假定每次生成n=100个标准正态分布N(0,1)随机数,并计算这些随机数在概率纸上对应散点的相关系数,一共重复m=1 000次,相关系数的直方图如图1左所示,其0.05下侧分位数为0.987 8。 图1 参考相关系数直方图(左)与F(10,10)的正态概率检验图 假设观测数据来自F(10,10)总体,即利用计算机随机生成100个F(10,10)随机数,其概率纸检验图如图1右所示,对应的相关系数r0=0.906 8。显然,它是一条曲线,可直观上判断观测数据不是来自正态总体。因为0.906 8<0.987 7,故拒绝原假设,即认为观测数据不是来自正态总体。可见,QQ图的直观判断与定量判断是一致的,且都与真实情况吻合。 假定观测数据来自总体F(10,10),χ2(6),分别利用计算机模拟1 000次,对应的简单相关系数如图2所示,正确判断的概率分别为1,0.990 0。显然,对于一般总体而言,本文中概率纸检验改进方法的正确率高,即概率纸改进方法可靠性高。 图2 总体F(10,10)(左)与χ2(6)(右)在正态概率纸检验下对应参考相关系数的直方图 假定观测数据来自总体t(3),t(30),分别利用计算机模拟1 000次,对应的简单相关系数如图3所示,正确判断的频率分别为0.903 0,0.045 0.这说明:假定数据来自总体F(x)(不是正态总体),如果F(x)与正态总体越接近,则正确判断的概率会越低。对于t分布而言,当其参数较大时,它非常接近正态分布,故否定原假设的可能性很低,即正确判断的概率很低。事实上,t(30)可以用N(0,1)近似,即两个总体几乎没有区分,即来自t(30)的数据检验为“不拒绝来自总体N(0,1)”也是合理的。 图3 总体t(3)(左)与t(30)(右)在正态概率纸检验下对应参考相关系数的直方图 进一步模拟,如果数据来自正态总体,在显著性水平取0.05的前提下,本文方法的正确率很高,接近0.95,这与假设检验理论相吻合。 (1)对数正态分布 (2)指数分布 设X~Exp(λ),即F(x)=1-exp{-λx},x≥0,则-ln(1-F(x))=λx,x≥0。它表明(x,-ln(1-F(x)))是一条过原点的直线,斜率为λ。实际上,(-ln(1-F(x)),x)也是一条直线。因为它们在本质上是一样的,只是斜率互为倒数。为便于表述与计算,本文采用前一种表示方法。所以,如果样本数据来自指数总体X,则散点图: 在概率纸上大体呈直线,且该直线过原点。相仿,若样本数据来自双参数指数总体: F(x)=1-exp{-λ(x-μ)},x≥0 (3)威布尔分布 在概率纸上大体呈直线,则样本数据来自威布尔总体,反之则否。 下面对改进的威布尔分布概率纸检验进行蒙特卡洛分析。假定观测数据来自F(10,10)总体,即利用计算机生成100个F(10,10)随机数xi,i=1,2,…,n。考虑以下假设检验:H0:F(x)=Weibull(m,x0)。其威布尔概率纸检验图如图4右所示,对应的相关系数r0=0.959 1。显然,它是一条曲线,可直观上判断观测数据不来自威布尔分布。 图4 F(10,10)的参考相关系数直方图(左)与的威布尔概率检验图 因为0.959 1<0.978 7,故拒绝原假设,即认为观测数据不是来自威布尔总体。可见,威布尔概率检验图的直观判断与定量判断是一致的,且都与真实情况吻合。进一步模拟可知,对于总体F(10,10),本文方法的正确率在80%附近,具有较大的参考价值。但客观来说,这有点偏低,主要是因为数据总体F(10,10)与威布尔分布具有一定的相似性。这也是所有检验存在的共性问题,即数据总体与检验总体有差异且差异越小,检验的效率越低。 假定观测数据来自总体Weibull(3,5),Exp(0.1),同上,一次模拟结果如图5和6所示。 对于总体Exp(0.1),r0=0.996 2>R0.05=0.978 2,故接受原假设,认为观测数据来自威布尔总体。这与威布尔概率检验图的结果一致,且都与事实相符,因为指数分布是特殊的威布尔分布。 图5 Weibull(3,5)的参考相关系数直方图(左)与威布尔概率检验图(右) 对于总体Weibull(3,5),r0=0.994 9>R0.05=0.976 4,故接受原假设,即认为观测数据来自威布尔总体。这与威布尔概率检验图的结果一致,且都与事实相符。 图6 Exp(0.1)的参考相关系数直方图(左)与威布尔概率检验图(右) 进一步模拟可知,对于总体Weibull(3,5)与Exp(0.1),本文方法的正确率很高,在99.5%附近。 本文根据传统的正态概率纸检验,通过生成正态随机数xi,i=1,2,…,n,并计算概率纸上对应随机数yi,i=1,2,…,n及二者简单相关系数,结合显著性水平确定假设检验的临界值。最后,将此方法推广到对数正态分布、指数分布、威布尔分布。通过大量仿真实验可以看出,通过将定性与定量判断相结合,提高了传统概率纸检验的客观性。注意,概率纸检验的正确率与数据来自总体有关,数据总体与检验分布有差异且差异越小正确率越低,如果二者一致,正确率接近95%(假定显著性水平为0.05),与假设检验理论相符。 [1] 刘军著,唐年胜,周勇,徐亮译.科学计算中的蒙特卡罗策略[M].北京大学出版社,2009. [2] Givens G H,Hoeting J A著,王兆军,刘民千,邹长亮等译.计算统计[M].北京:人民邮电出版社,2009. [3] 孟杰,王欣,张然.修正Benford分布律及其模拟研究[J].统计与信息论坛,2017,32 (9). [4] 王佐仁,徐生霞.蒙特卡罗方法下线性模型的异方差性检验方法[J].统计与信息论坛,2016,31 (11). [5] 魏艳华,王丙参编著.概率论与数理统计[M].成都:西南交通大学出版社,2013. [6] 曹晋华,程侃著.可靠性数学引论[M].高等教育出版社,2006. [7] 朱力行,许王莉著.非参数蒙特卡罗检验及其应用[M].北京:科学出版社,2008. [8] 郝丽,刘乐平,申亚飞.统计显著性:一个被误读的p值[J].统计与信息论坛,2016,31 (12) .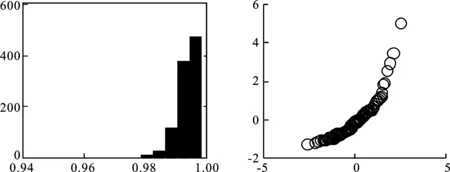
三、概率纸检验及其改进的推广
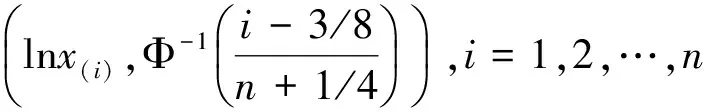
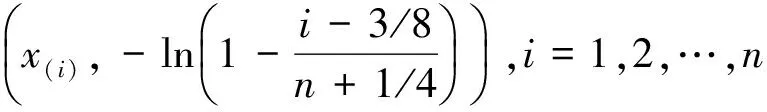
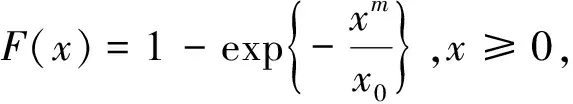
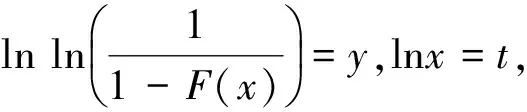
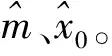
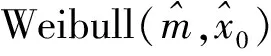
四、结论
