基于BIC的粗糙集择优和属性约简
2018-03-20杨贵军
杨贵军,于 洋
(天津财经大学 中国经济统计研究中心,天津 300222)
一、引 言
在大数据背景下,从海量数据中挖掘有价值信息的方法研究日益重要。粗糙集是Pawlak于1982年提出的一种数据挖掘方法[1],具有分类规则易于理解、不受数据分布类型限制等优点,现已广泛应用于经济[2-4]、人工智能[5-6]等领域。现有粗糙集的研究主要集中于粗糙集构造方法的完善以及针对不确定性数据和模糊性数据的粗糙集构造等问题[7-8],而粗糙集优良性评估标准一直是研究重点,直接影响到粗糙集择优与粗糙集属性约简。粗糙集择优注重对采用不同方法构建的多个粗糙集进行择优,属性约简注重对剔除冗余信息属性的多个粗糙集进行比较。现有的粗糙集优良性评价目的是在多个备选粗糙集中选择出预测准确度高的粗糙集,而粗糙集的优良性评估准则仍是目前具有挑战性的问题。
粗糙集是根据研究对象的条件属性与决策属性之间的关系建立分类规则,以识别新观测对象所属类别。粗糙集优良性评估注重粗糙集的分类能力,主要对粗糙集的分类性能进行评价,如Düntsch等人利用随机化统计方法考查粗糙集的分类规则是否仅基于少数随机观测得到,试图分析粗糙集分类的可信度[9]。很多文献也以分类误判率或分类正确率来评价粗糙集分类的正确性,如Hu等人构建了基于数据库系统的新粗糙集,并进行了粗糙集属性约简[10],而采用分类正确率考量新方法具有更高的计算效率;Jaworski给出了衡量粗糙集分类规则准确性和覆盖度的估计指标,并基于这些指标对粗糙集属性进行约简和粗糙集优良性评价[11];Cornelis等人总结了使用模糊容差关系进行粗糙集属性约简的方法,给出的实际分析案例具有高正确率[8];邓维斌等人建立了基于优势关系粗糙集的自主式学习模型,并用正确率和平均绝对误差评价粗糙集分类性能[12];翟育明等人构造了基于(α,β)集对限制优势关系的粗糙集[13],而新模型分类具有更低整体误判率。
综上所述,现有研究注重粗糙集分类的准确性,大多文献选择分类误判率作为粗糙集优良性评估标准,然而粗糙集在测试集中的误判率最低,但在新数据集的预测准确度并不总是最高。本文对于京津冀务工经商高学历流动人口数据集,分别采用基于最大概率的粗糙集方法和基于贝叶斯的粗糙集方法构造了500个粗糙集,其中在测试集中最低误判率的500个粗糙集中,只有422个粗糙集在新数据集中预测准确度最高。误判率标准对评价粗糙集优良性很重要,而只注重粗糙集的判错率则过于简易,未考虑粗糙集的模型复杂度,特别是在测试集中多个粗糙集误判率差异小的情况,采用误判率标准不易选出在新数据集中预测准确度高的粗糙集。
针对决策属性为两分类的数据集,笔者引入了基于AIC准则的粗糙集择优方法并演示其良好的性质[14]。本文引入基于贝叶斯信息准则(BIC)的粗糙集择优和属性约简方法,先利用粗糙集的分类规则定义解释变量,将决策属性作为因变量,并构造Logistic模型以表达该粗糙集的分类;采用最大似然方法估计Logistic模型参数,用拟合模型的BIC值作为该粗糙集的BIC值进行粗糙集择优和属性约简。新方法兼顾了粗糙集的分类正确概率与复杂度,能有效避免过拟合问题,数据分析结果显示当多个粗糙集在测试集中误判率差异小时,新方法能更好地选择预测准确度高的粗糙集。
二、基于BIC的粗糙集择优方法
对于同一数据集,采用不同构造方法所得到的粗糙集并不总是一致的,其误判率和预测准确度也往往有差异。目前,粗糙集构造方法主要有基于最大概率的粗糙集方法和基于贝叶斯的粗糙集方法[15]。
设有n个研究对象,记U={u1,u2,…,un},X={x1,x2,…,xk}为条件属性,k表示条件属性个数,Y为决策属性,这里约定其为两分类变量,取值为0或1。为简化叙述,将一个类别记为c类,另一个类别记为1-c类。基于最大概率的粗糙集方法先计算第i(i=1,2,…,n)个个体ui的条件属性xi1,xi2,…,xik在第c类的概率,计算公式为:
如果P(yi=c|xi1,xi2,…,xik)≥P(yi=1-c|xi1,xi2,…,xik),将个体ui判为第c类,分类规则记为:
r∶xi1,xi2,…,xik→yi=c
ifP(yi=c|xi1,xi2,…,xik)
≥P(yi=1-c|xi1,xi2,…,xik)
(1)
其中条件属性为xi1,xi2,…,xik,将属于1-c(c=0,1)类的第i(i=1,2,…,n)个个体ui,判为第c(c=0,1)类的误判损失,记为λ(yi=c|xi1,xi2,…,xik)≥0。基于贝叶斯的粗糙集方法,先计算本属于1-c(c=0,1)类的第i(i=1,2,…,n)个个体ui的条件属性xi1,xi2,…,xik被判为第c类的误判平均损失为:
αc=λ(yi=c|xi1,xi2,…,xik)·
P(yi=c|xi1,xi2,…,xik)·
P(xi1,xi2,…,xik|yi=1-c)
如果αc≤α1-c,则将个体ui判为第c类,分类规则为:
r∶xi1,xi2,…,xik→yi=cifαc≤α1-c
(2)
基于最大概率的粗糙集方法和基于贝叶斯的粗糙集方法所构造的粗糙集分类规则并不总是相同的,相应粗糙集的误判率也往往是不一样的。
分类误判率侧重评价粗糙集分类的准确性,与此类似,Logistic模型也适用于数据分类,而且往往具有较高的分类准确性。本文引入的基于BIC的粗糙集择优方法试图组合两类模型以得到更高的分类准确性。这里,将决策属性yi作为Logistic模型的因变量,将判为第一类的分类规则定义为解释变量,记为zi=(zi1,zi2,…,zim)。zij为由第j个分类规则所定义的解释变量,m为新变量个数,i=1,2,…,n(n为观测个数)。为避免共线性问题,在定义赋值新变量时仅选取判为第一类的分类规则,构建的Logistic模型为:
(3)
采用最大似然法估计模型(3)的参数,并计算其BIC值为:
(4)
三、基于BIC的粗糙集属性约简方法
对于给定数据集,基于最大概率的粗糙集方法和基于贝叶斯的粗糙集方法所构造的粗糙集,其属性常常会存在冗余信息,而剔除冗余信息,并进行属性约简,则可得到优化的粗糙集。BIC准则也可以作为属性约简的标准,称其为基于BIC的粗糙集属性约简,具体方法如下:
对于需要属性约简的粗糙集,将决策属性yi作为Logistic模型的因变量,选取判为第一类的分类规则定义为解释变量,构建Logistic模型式(3),计算其BIC值,记为BIC(all);令p为粗糙集的属性总数,对于j=1,2,…,p利用粗糙集的分类规则,依次去掉其属性列aj=(a1j,a2j,…,anj)′,合并重复的规则并按照最大概率原则处理分类矛盾的规则,基于处理后的规则分别计算相应Logistic模型的BIC值,记为BIC(-aj),比较所有BIC(-aj)(j=1,2,…,p),选择其中最小值与BIC(all)比较:若其不大于BIC(all),则剔除最小BIC值对应的aj;否则,对应BIC(all)的粗糙集为在BIC准则下的最优粗糙集;剔除粗糙集的属性,需要再利用粗糙集的分类规则,重复上述过程,直至选出在BIC准则下的最优粗糙集。这里,将BIC值作为粗糙集属性约简的标准,选出预测准确性高的粗糙集。本文关注二分类决策属性的情况,基于BIC的粗糙集属性约简方法也可推广到多分类决策属性的情况。
四、应 用
将基于BIC的粗糙集择优方法和基于BIC的粗糙集属性约简方法用于分析两组数据:一是京津冀地区的流动人口生存发展状况调查数据,考察京津冀地区务工经商高学历流动人口的特征;二是加州大学欧文分校数据挖掘研究数据库中的Breast Cancer Wisconsin(Original)(以下简称Breastcancer)数据集,分析乳腺癌细胞的主要特征。
(一)京津冀务工经商高学历流动人口的特征分析
随着中国经济发展以及京津冀协同发展政策的不断推进,京津冀地区已成为继长三角、珠三角地区后最引人注目的流动人口聚集地,其中外出务工经商是人口流动的主要原因。高学历人群作为具有高人力资本的群体,在流动人口中占有相当比例,而研究京津冀务工经商高学历流动人口的主要特征,能够帮助政府更好地服务和管理流动人口。本文考察的高学历包括大学专科、本科学历;数据来源于2015年国家卫生计生委全国流动人口生存发展状况及卫生计生委服务管理抽样调查的京津冀地区数据;经数据预处理后共得到有效样本4 336份,其中北京2 307份、天津657份、河北1 372份;高学历人口的基本信息包括年龄xi1、性别xi2、户口登记类型xi3、婚姻状况xi4;流动相关信息包括本次流动时间xi5;经济情况包括恩格尔系数xi6、总支出占总收入比重xi7;将7个可能对流动原因有影响的变量作为条件属性;将流动原因是否为务工经商作为决策属性yi,为1者代表是、为0者代表否;其中年龄分为15~20岁、21~35岁、36~60岁、61岁以上的四水平分类变量;本次流动时间为以月计的连续变量;恩格尔系数由月平均食品支出/月平均总收入得到,分为0.4以下、0.4及以上的二水平分类变量;总支出占总收入比重由月平均总支出/月平均总收入得到,分为0.5以下、0.5及以上的二水平分类变量。
1.基于BIC的粗糙集择优。分别采用基于最大概率的粗糙集方法和基于贝叶斯的粗糙集方法,构建粗糙集分类规则,可以得到两类不同的京津冀地区务工经商高学历流动人口的特征。基于BIC的粗糙集择优方法能有效选择出具有高预测准确度的一类特征,因此本文基于BIC对两个粗糙集进行择优。对7个条件属性xi1,xi2,xi3,xi4,xi5,xi6,xi7离散化并进行属性约简,约简后剩余4个属性,记为xri1,xri3,xri4,xri5,结果见表1的第2~5列。先采用基于最大概率的粗糙集方法构建分类规则,选取判为第一类的分类规则,去掉出现频数少的分类规则;再利用分类规则定义解释变量并且赋值作为Logistic模型的解释变量,如表2所示。对应训练集和测试集的新变量z的取值见表1的第7~10列所示,决策属性的取值见表1第6列。

表1 对应训练集和测试集的新变量表

表2 Logistic模型解释变量表
将决策属性作为因变量建立Logistic模型,计算相应模型的BIC值为2 885.13。同样地,采用基于贝叶斯的粗糙集方法,计算相应Logistic模型的BIC值为2 927.38。采用基于最大概率的粗糙集方法得到的粗糙集BIC值更小,由其所得规则归纳出务工经商高学历流动人口的特征为年轻人、具有农业或非农业户口(即不包括农业转居民和非农业转居民户口)、未婚且流动时间较短,或年轻人、具有农业或非农业户口(即不包括农业转居民和非农业转居民户口)、已婚且流动时间较长,其归纳结果较为合理。
为进一步验证基于BIC的粗糙集择优方法在本实例中的有效性,本文将该方法与传统的基于误判率的粗糙集择优方法进行比较。从该数据集中随机抽取80%的数据作为训练集与测试集,用于粗糙集的构建与选择;其余20%的数据作为预留数据集,用于比较误判率准则和BIC准则的粗糙集选择效果,即取训练集容量为2 775、测试集容量为694、预留数据集容量为867,为避免训练集、测试集与预留数据集的选取对结果造成显著影响,随机抽取训练集、测试集与预留数据集,采用五折交叉验证方法来进行计算,重复模拟100次。为比较BIC准则和误判率准则,选择在预留数据集中最高预测准确度的粗糙集为最优,这里最高预测准确度是指粗糙集在预留数据集中的误判率最低。若所选粗糙集在测试集的误判率最小且在预留数据集上的预测准确度最高,则认为采用误判率准则选出了“正确”粗糙集,否则认为选出了“错误”粗糙集;若所选粗糙集的BIC值最小且在预留数据集上的预测准确度最高,则认为BIC准则选出了“正确”粗糙集,否则认为选出了“错误”粗糙集。
对于该数据集,在100次重复的五折交叉验证计500次过程中,分别采用BIC准则和误判率准则进行粗糙集选择的结果见表3第1行;表3的第2~5列,分别给出了采用误判率准则选择粗糙集的错误次数和正确次数;采用BIC准则选择粗糙集的错误次数和正确次数:第6列给出了两种准则都正确选择粗糙集的次数,第7列给出了BIC准则正确选择粗糙集而采用误判率准则错误选择粗糙集的次数。对于采用基于最大概率的粗糙集方法和基于贝叶斯的粗糙集方法所构造的两个粗糙集在测试集的误判率之差小于3%的情况,BIC准则和误判率准则选择粗糙集的结果见表3第2行;由表3第1行知,采用误判率准则和BIC准则同时正确选择粗糙集的情况达到384次,正确选择粗糙集的比率高达84%以上。与误判率准则相比,BIC准则适用于粗糙集的选择和评价,选出的粗糙集具有较高的预测准确率。此外,多次出现了BIC准则选择正确粗糙集,而误判率准则选择了错误粗糙集的情况,此时BIC准则优于误判率准则。总之,BIC准则可以代替误判率准则择优粗糙集,是粗糙集择优的备选准则。表3第2行数据显示,两种方法所构造的粗糙集在测试集的误判率之差小于3%的情况共有353次,其中有39次BIC准则选出“正确”粗糙集,而误判率准则选了“错误”的粗糙集,在这种情况下BIC准则优于误判率准则,BIC准则选出正确粗糙集的频率更高,具有更好的预测准确度。
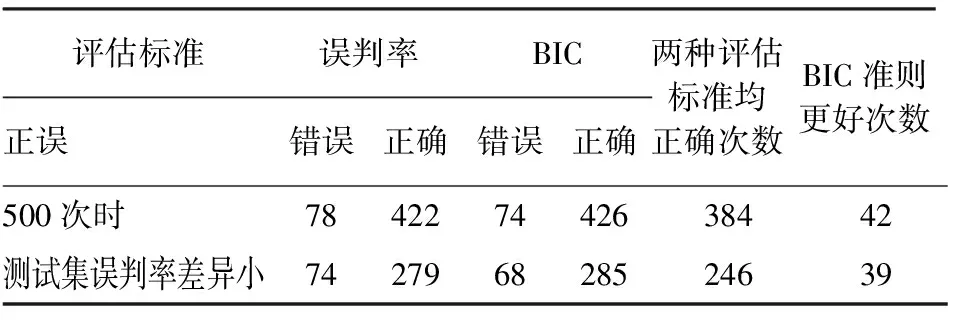
表3 两种准则选择结果对比情况表
2.基于BIC的粗糙集属性约简。上节得到京津冀地区务工经商高学历流动人口特征的粗糙集均是采用传统的粗糙集属性约简方法,即由信息熵方法得到的,亦即用信息熵方法约简属性时保留了多个属性,规则涵盖内容较多。因此,本文采用基于BIC的粗糙集属性约简方法进行分析,找出更精炼的规则及影响京津冀务工经商高学历流动人口的关键特征:先利用基于最大概率的粗糙集方法构建粗糙集分类规则;再针对不同属性个数的分类规则,采用基于BIC的粗糙集属性约简方法对所得多个粗糙集进行选择,约简后属性为年龄、婚姻状况及本次流动时间3个属性,并由其规则可得到基于务工经商原因流动的高学历人群的特征为年轻人、未婚且一次流动时间较短,或年轻人、已婚且一次流动时间较长的结论。归纳结果相比上节更加精炼,这也与笔者已知的实际情况较为吻合。
为进一步验证该方法在本实例中的有效性,本文将基于BIC的粗糙集属性约简方法与信息熵方法进行对比,用预测准确度作为比较标准。针对该数据集,取训练集容量为3 469、测试集容量为867,随机抽取训练集与测试集,采用五折交叉验证方法来进行计算,重复模拟100次。对于该数据集,在100次五折交叉验证共500次过程中,分别采用信息熵方法和BIC方法进行粗糙集属性约简的结果见表4。表4的第1行给出了500次采用两种方法进行粗糙集属性约简的误判率均值;第2行给出了500次分别采用两种方法得到的属性约简后属性个数均值;第3行给出了500次分别采用两种方法得到的属性约简后的粗糙集分类规则个数均值;第4行给出了500次中与信息熵方法相比BIC方法的误判率不大于或更小次数。由表4知:基于BIC的属性约简得到的属性个数与规则个数平均而言小于采用信息熵方法,且采用BIC方法的误判率平均低于采用信息熵方法,其误判率不大于信息熵方法的次数达到401次。

表4 两种方法单独约简结果对比情况表(500次时)
图1是两种方法属性约简结果的误判率密度图,给出了采用信息熵方法和采用BIC方法进行500个粗糙集属性约简的误判率情况,显示采用BIC方法进行属性约简后误判率小的粗糙集的频率更高更集中。
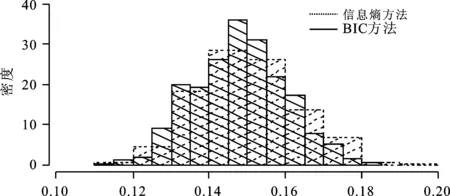
误判率
图2和图3给出了采用信息熵方法和采用BIC方法进行500个粗糙集属性约简的属性与规则个数的详细情况。图2是两种方法约简结果属性个数的密度图,显示采用BIC方法进行属性约简得到的属性个数普遍更少,属性个数小的频率高。图3是两种方法约简结果的规则个数的密度图,显示采用BIC方法进行属性约简得到的规则个数普遍更少,规则个数小的频率高。
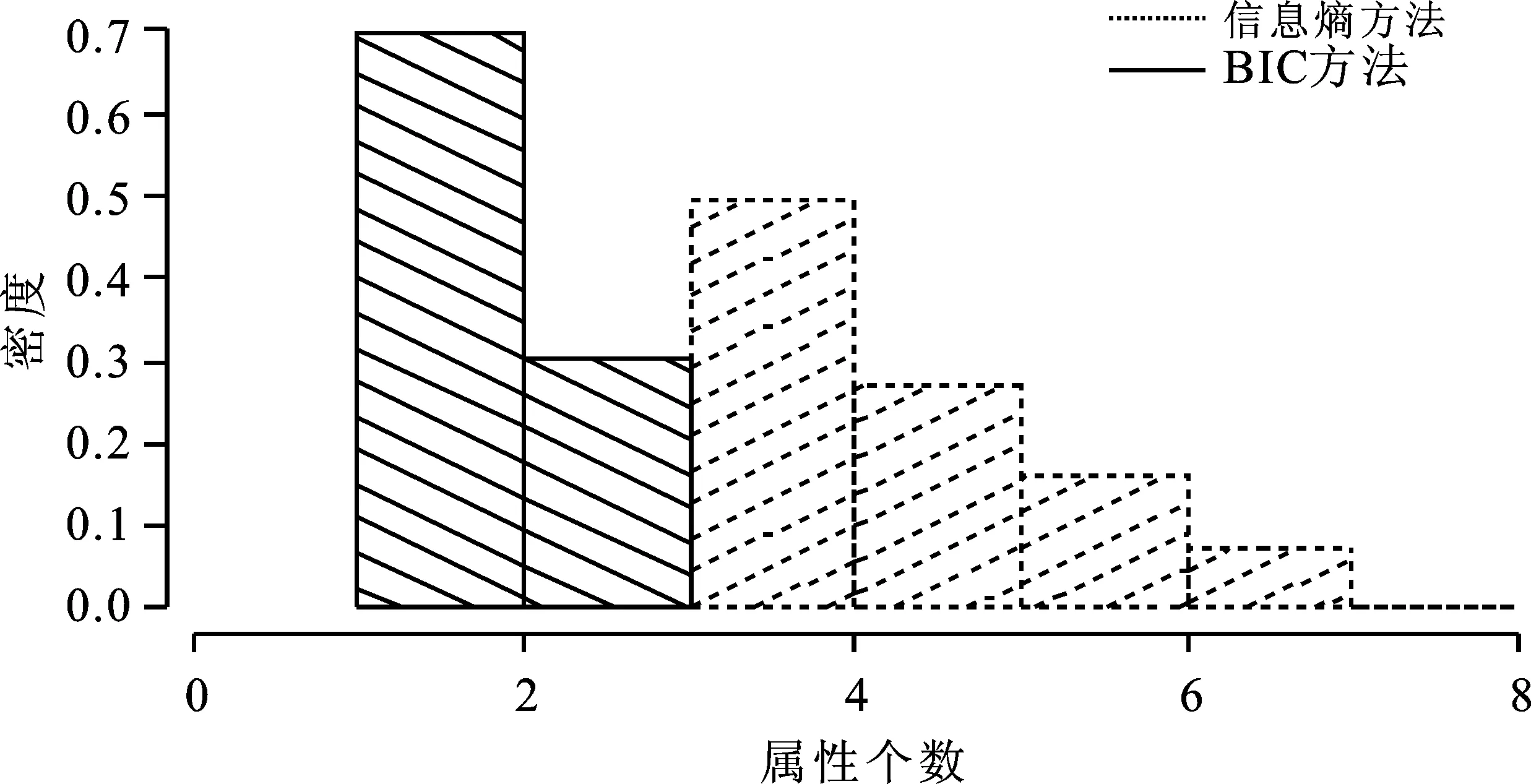
图2 两种方法约简结果属性个数密度图
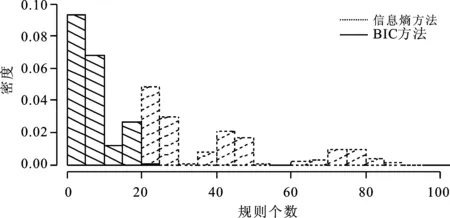
图3 两种方法约简结果规则个数密度图
综合上述分析,基于BIC属性约简方法的属性个数与规则个数普遍小于采用信息熵方法,且采用BIC方法的误判率普遍低于信息熵方法,BIC方法的属性约简程度相对更好。
3.基于BIC和信息熵组合的粗糙集属性约简。基于BIC的粗糙集属性约简方法可与信息熵方法组合使用,组合方法计算量相对较少,消除了冗余信息,利于识别出务工经商高学历流动人口的关键特征。先给定数据集,采用信息熵方法进行属性约简,得到的结果包括年龄、户口登记类型、婚姻状况、本次流动时间共4个属性,识别出的高学历流动人口的特征较多;在得到的粗糙集分类规则的基础上,再采用BIC方法进一步属性约简,得到年龄、婚姻状况、本次流动时间3个属性,相比原始数据信息减少了4个属性,约简力度大;仍与信息熵方法比较,进行100次五折交叉验证,得到的500次过程中先用信息熵方法再用BIC方法,组合进行粗糙集属性约简的结果见表5。

表5 两种方法结合约简结果情况对比(500次时)
由表5可知:采用两种方法组合进行属性约简,可有效减少属性个数与规则个数,且组合方法的误判率平均低于只采用信息熵方法,其误判率不大于信息熵方法的次数达到396次,频率较高。
(二)乳腺癌细胞特征分析
Breastcancer数据集为威斯康星大学Wolberg博士有关乳腺癌的临床病例数据,考察不同样品属于良性还是恶性,共包含699个样品,剔除缺失的16个数据,条件属性包括肿块厚度、细胞大小均匀性、细胞形状均匀性、边缘粘、单上皮细胞大小、裸核、乏味染色体、正常核、有丝分裂;决策属性为1者代表良性,为0者代表恶性。
具体分析过程类似第一个例子。采用五折交叉验证方法,针对基于BIC的粗糙集择优方法取训练集容量为437、测试集容量为109、预留数据集容量为137,针对基于BIC的粗糙集属性约简方法和基于BIC和信息熵组合的粗糙集属性约简方法,取训练集容量为546、测试集容量为137,重复100次,结果见表6。
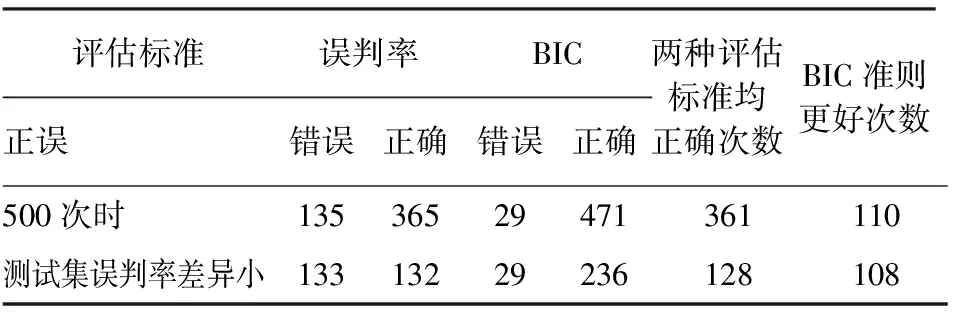
表6 两种准则选择结果对比情况表
表6显示:采用误判率准则和BIC准则同时正确选择粗糙集的情况达到361次,正确率高于72%,出现110次BIC准则选择了正确粗糙集而误判率准则选择了错误粗糙集的情况;特别是在测试集误判率之差小于3%的情况下,有108次BIC准则选了“正确”粗糙集而误判率准则选了“错误”的粗糙集,BIC准则选出正确粗糙集的频率更高。

表7 两种方法单独约简结果对比情况表(500次时)

表8 两种方法结合约简结果对比情况表(500次时)
表7显示:基于BIC的属性约简得到的属性与规则个数平均而言小于信息熵约简方法,误判率相对更低,其误判率不大于信息熵方法的次数达到340次;表8显示:采用两种方法组合进行属性约简,相比只采用信息熵方法,约简力度更大,误判率更低,其误判率不大于信息熵方法的次数达到347次。
综上所述,BIC方法引入了模型参数个数惩罚,惩罚力度较大,特别是对于数据集采用信息熵方法属性约简后数据维数较高的情况,可引入基于BIC的粗糙集属性约简方法进一步提高约简效果。相比于参考文献[14]的研究,本文选择的BIC准则比AIC准则更倾向于模型约简,其约简程度要更强。
五、结 论
BIC准则是常用的统计模型选择准则之一。针对粗糙集优良性评估,本文引入了BIC准则,构建了基于BIC的粗糙集择优和属性约简方法。新方法综合考虑了模型分类正确概率与模型复杂度,并选择了更高预测准确度的粗糙集,以完善粗糙集优良性评估准则,为粗糙集择优与属性约简提供了新思路。实际数据分析结果显示:基于BIC的粗糙集择优方法与误判率准则选择正确粗糙集的频率都较高;对于误判率差异小的多个备选粗糙集,BIC准则选出高预测准确度粗糙集的频率更高;基于BIC的粗糙集属性约简方法比信息熵方法约简程度更高,并可与信息熵方法结合使用,以进一步提高约简效果。
[1] Pawlak Z.Rough Sets[J].International Journal of Computer and Information Sciences,1982,11(5).
[2] Tay F E H,Shen L.Economic and Financial Prediction Using Rough Sets Model[J].European Journal of Operational Research,2002,141(3).
[3] 曹黎侠,黄光球,况湘玲.基于粗糙集理论的第三方支付平台的效益问题[J].统计与信息论坛,2016(1).
[4] 王宏智,高学东,赖媛媛.基于灰粗集属性知识简约算法的海运规则发现[J].统计与信息论坛,2017(1).
[5] Qian Y H,Liang J Y,Pedrycz W,et al.An Efficient Accelerator for Attribute Reduction from Incomplete Data in Rough Set Framework[J].Pattern Recognition,2011,44(8).
[6] 邓大勇,卢克文,苗夺谦,等.知识系统中全粒度粗糙集及概念漂移的研究[J].计算机学报,2016,39.
[7] Qian Y H,Liang J Y,Pedrycz W,et al.Positive Approximation:An Accelerator for Attribute Reduction in Rough Set Theory[J].Artificial Intelligence,2010,174(9/10).
[8] Cornelis C,Jensen R,Hurtado G,et al.Attribute Selection with Fuzzy Decision Reducts[J].Information Sciences,2010(2).
[9] Düntsch I,Gediga G.Statistical Evaluation of Rough Set Dependency Analysis[J].International Journal of Human-Computer Studies,1997,46(5).
[10] Hu X H,Lin T Y,Han J.A New Rough Sets Model Based on Database Systems[J].Fundamenta Informaticae,2004,59(2).
[11] Jaworski W.Rule Induction:Combining Rough Set and Statistical Approaches[C].Rough Sets & Current Trends in Computing,2008.
[12] 邓维斌,王国胤,胡峰.基于优势关系粗糙集的自主式学习模型[J].计算机学报,2014,37(12).
[13] 翟育明,蔡红,郭斌.(α,β)集对限制优势粗糙集及决策模型[J].系统管理学报,2014,23(3).
[14] 杨贵军,于洋,孟杰.基于AIC的粗糙集择优方法[J].模糊系统与数学,2018,32(1).
[15] 范霄文.基于粗糙集的定性数据分析方法研究[D].厦门:厦门大学,2008.
