增量式隐私保护频繁模式挖掘算法

张亚玲，王 婷，王尚平

(西安理工大学 计算机科学与工程学院，西安 710048)(*通信作者电子邮箱ylzhang@xaut.edu.cn)

0 引言

随着信息与网络技术的飞速发展，数据挖掘,尤其是频繁项集的挖掘[1]在揭示各类隐藏的模式或知识的同时，也相应地产生了隐私保护方面的隐忧，因为在数据挖掘过程中一些个人隐私或者共同隐私容易受到侵犯。如消费者在使用信用卡、会员卡、医疗保健卡和电子商务网站购物等活动中，个人信息很容易被公司或企业获取，因此，隐私保护[2]和信息安全[3]成为数据挖掘中一个迫切需要解决的问题，越来越引起人们的广泛关注。

隐私保护技术是指采用某种技术来隐藏敏感数据或敏感知识,它对于能否有效地隐藏数据或知识以及能在多大程度上进行隐藏有重要影响。目前，在隐私保护数据挖掘中所采用的算法主要分为两类：1)基于安全多方计算技术的方法[4-5]；2)基于随机的方法[6-7]。

基于随机的方法根据具体的需要对原始数据库中的记录进行模糊化处理的同时保持数据的统计特性，在经过处理的数据库上进行数据挖掘，通过对数据的原始统计特性的估计来得到较为准确的处理结果，同时又不泄露用户的原始数据。在布尔数据集上基于概率变换的支持度重构的方法是基于随机方法的一个重要研究分支。文献[8]结合隐私保护查询限制与数据干扰这两种基本策略提出一种部分隐藏的随机化回答(Randomized Response with Partial Hiding， RRPH)算法，在对原始数据进行隐藏与变换为基础上进行数据干扰，之后采用高效且简单的频繁项集生成算法，最后进行隐私保护关联规则挖掘。该算法存在重构真实项集支持度上的指数级运算和频繁扫描数据库的缺点，使得其在效率上受到了严重的制约。文献[9]中提出了RRPH算法的改进算法，该算法使用集合运算和分治策略对RRPH进行改进，消除重构真实数据集支持度上的指数级别的巨大的运算量。然而，由于Apriori需要多次对数据库进行扫描，文献[9]的算法效率仍然会受到多次扫描数据库的影响。针对以上问题，本文的研究思路是，首先引入bitmap[10]对数据库中的事务进行表示，避免了算法执行中对数据库的多次扫描；其次，通过引入增量更新模型，使得算法在面临数据更新问题时，仍然具有高效性。

1 RRPH算法及其改进算法的分析

部分隐藏的随机化回答(RRPH)算法[8]是一种基于部分隐藏随机化回答技术的隐私保护的频繁模式挖掘算法，该算法结合查询限制和数据干扰两种策略，对随机化参数的选择没有限制,不需要额外的信息,该算法适用于分布式数据库和集中式数据库。

RRPH算法对数据的随机化隐藏的过程为：对于布尔类型的数据库，选定随机参数p1,p2,p3，其中p1+p2+p3=1且0≤p1,p2,p3≤1，对于数据库中的项a∈{0,1},设r1=a,r2=1-a,r3=0,给定随机函数r(a)和函数pj的概率取值rj(j=1,2,3)。假如数据库中属性的个数为k，则原始事务A=(a1,a2,…,ak)经过干扰之后转变为事务B=(b1,b2,…,bk)的概率可以由B=R(A)计算得到，其中bi=r(ai)，即bi取值为ai的概率为p1,取值为ai的反的概率为p2，取值为0的概率为p3。

针对RRPH算法在重构频繁项集真实支持度时的指数级别的运算量而导致算法效率下降的问题，文献[9]采用集合运算和分治策略提出了改进的RRPH算法，消除了重构真实支持度时指数级别的复杂度，提高了算法效率。

由于文献[9]的改进主要是针对RRPH算法的重构支持度的改进，该算法仍然需要完全的数据库扫描以及呈指数级别增长的比较操作，因此算法的效率仍是制约该算法的关键问题。此外，文献[8-9]都没有考虑数据增量更新的问题。事实上，在大数据时代，每天会产生数以万计的增量数据，这些增量数据很有可能对数据挖掘结果产生巨大的影响。具有增量更新性质的隐私保护的频繁模式挖掘算法更具有实际意义。本文将基于以上两个问题，提出一种增量的基于位图的RRPH(Incremental Bitmap-based RRPH, IBRRPH)算法。

2 IBRRPH算法的原理和分析

2.1 使用bitmap技术转换数据

假设用R来表示关系模式，A={A1,A2,…,An}表示组成R的属性集合，任一属性Ai在Di(1≤i≤n)的范围内取值，则定义在该模式上元组的真实取值范围为U=D1×D2×…×Dn。

定义1 给定r是关系模式R上的任一关系，任一属性Ai(1≤i≤n)在r上的真实取值范围简称活动域，表示为ADom(Ai,r)={d∈Di|∃t∈r,t(Ai)=d}。通常可以将ADom(Ai,r)简称为ADom(Ai)。

定义2 给定r是关系模式R上的任一关系，则ADom(Ai)到r的映射F可以表示为F:V→ADom(Ai)，V表示r中元组的全集。ADom(Ai)中任何一个可能值表示为c(c∈ADom(Ai))，关系r中在Ai上值为c的元组全集称为c在r上的逆像，表示为F-1(c)={t|t∈V,t(r)=c}。

定义3 假设R上的任一关系r含有m个元组，而r在Ai上的某一可能取值表示为c(c∈ADom(Ai))，则可以使用m位二进制数来代表关系r在Ai上值为c的位置，称此m位二进制数为关系r中在Ai上值为c的bitmap，记为Bin(Ai,c)。如果ts是r中第s个元组，倘若ts∈F-1(c)，则Bin(Ai,c)中第s位的取值范围为{0,1}。

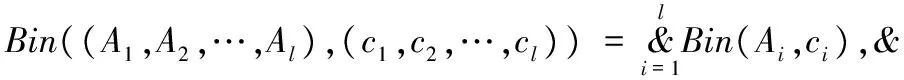
定义4 假设任一关系r中包含N个元组，r在(A1,A2,…,Al)上的值为(c1,c2,…,cl)，则根据定义3，用bitmap可定义为Bin((A1,A2,…,Al),(c1,c2,…,cl))。设P=(c1,c2,…,cl)为r上模式，其长度为l，那么P的支持度计数表示为freq(P)=Count(Bin((A1,A2,…,Al),(c1,c2,…,cl)))，函数Count()表示bitmap中1的数量。假设最小支持度阈值为θ(0<θ<1)，当freq(P)≥θN时，P是频繁模式；否则P不是频繁模式。

定义5 给定数据库D共包含N条事务{T1,T2,…,Tn}，其中Ti是属性集{A1,A2,…,An}的子集，则D可视为共有N个元组的关系，其中任意事务Ti都含有n个属性，ADom(Ai,r)={‘0’,‘1’}。如果任一事务Tj在Ai上取值是‘1’，则意味着Ai出现在事务Tj中，为‘0’则意味着Ai没有出现在事务Tj中。

原始数据库表中的任意一条记录在bitmap中具有唯一的位置偏移。每个事务均匀地分布在这一固定的位置偏移上。

伴随着使用bitmap对数据库中记录的转变，算法中的计数方式也随之发生了改变，BRRPH算法采用“位与”操作作为计数方式，可以有效提高支持度的计数速度。

设存在表1所示的事务数据库，则bitmap规范之后的交易列表如表2所示。其中：TID为事务ID，ItemId为项ID。

表1 事务数据库D

表2 规范之后的交易列表

使用位与运算可以快速对项集计数。例如：项集{I1}的bitmap表示为100110111；{I2}的bitmap表示为111101011，则{I1，I2}的bitmap表示为10010001，因此，统计{I1，I2}的bitmap表示100100011中1的个数，即可得项集{I1，I2}的支持度为4。通过对bitmap中的项集交集操作，可以提高算法的效率。

2.2 BRRPH算法

基于Bitmap的部分隐藏的随机化回答(Bitmap-based Randomized Response with Partial Hiding, BRRPH)算法是基于Bitmap技术对文献[9]算法进行的改进，目标是提高算法的效率。BRRPH算法可以描述为以下3步：

步骤1 预先设置随机化参数p1,p2,p3的值，采用文献[9]算法对数据库中的原始记录进行隐藏或变换。

步骤2 将经过扭曲的数据保存在Bitmap文件中，使用Bitmap技术中的位与技术，可以提高算法得到频繁项集的效率。

步骤3 在转化后的文件上使用文献[9]算法进行数据挖掘，结合Bitmap计算和分治策略等方法重构原始数据的真实支持度，从而得到频繁项集。

BRRPH算法的总体框架如图1所示。

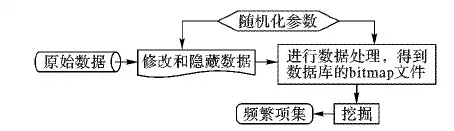
图1 BRRPH的总体框架

2.3 IBRRPH算法原理

2.3.1 增量更新算法基础

数据库中所包含的数据并不是一成不变，而是会随着时间的流逝而产生或大或小的变化，由于数据库的更新，会引入新的关联规则并使一些现有的关联规则失效，频繁项集也存在类似的更新问题。一般情况下，人们更专注于设计和研究隐私保护的关联规则挖掘方面的相关算法，却忽略了数据库发现的规则只反映数据库的当前状态这一事实。为了使揭露的规则稳定可靠，应在相当长的一段时间内收集大量数据。所以，在算法的设计中，要使研究更具有实际意义，不仅要关注与设计频繁模式关联规则挖掘算法，更要解决其更新带来的相关规则的变化。数据库中的事务有增加和减少两种不同的变换情况，应对这两种变换的基本策略没有太大差异，减量型挖掘算法可以对比增量型挖掘算法完成，本文将讨论数据增量型频繁模式的挖掘算法。

如图2所示，D为以前的旧的数据库，D+为增加的数据库，D′为新增一些数据之后的新数据库。在增量式挖掘中，主要解决当一个数据集D+增加到原来的数据库中时，引入新的关联规则并使一些现有的关联规则[11]失效。本文在BRRPH算法的基础上加入了增量更新技术，用于维护数据挖掘过程中发现的关联规则。

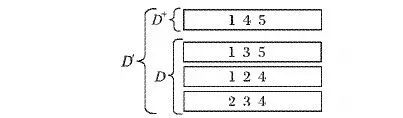
图2 数据库增量示意图

针对数据库中数据新增的问题，首先想到的方法是在整个更新的数据库上重新运行关联规则挖掘算法。这种方法虽然简单，却造成了之前挖掘结果的极大浪费。最初在找出旧的大项目集时完成的所有计算都被浪费，新的频繁项集都必须重新开始计算。文献[12]提出了一种有效的算法——FUP(Fast UPdate)，用于计算更新数据库中的大项集。在FUP中旧的大项目信息可以重复使用。此外，获得新数据库的频繁项集之后，便可以大量修剪候选项集。FUP算法的优势主要体现在减量式和增量式数据挖掘中，如分布式环境中并行处理大数据、使用改进的增量式关联规则数据挖掘算法分析警报信息、增量式计算等。本文将用到FUP算法中介绍的引理。

设A.supportD表示属性集A在原始数据库D中的支持度，A.supportD+表示属性集A在增加的数据库D+中的支持度。A.supportD′为增加一部分数据库后新数据库D′中属性A的支持度，d表示原始数据库D的事务个数，d+表示增加的数据库D+的长度，Lk是D中的频繁k项集，Lk′是D′中的频繁k项集，Ck是第k次迭代产生的候选k项集，那么，存在以下增量更新的性质[12]。

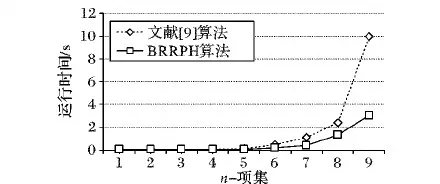
性质1 1项集A在原始数据库D中不为频繁1项集，在数据库D′中不为频繁1项集，当且仅当A.supportD′

性质2 1项集A在原始数据库D中不是频繁项集，A.supportD+>d+×c是A在数据库D′中为频繁1项集的必要不充分条件。

性质3 {A1,A2,…,Ak-1}在第k-1次迭代中是原始数据库D中的频繁项集，即{A1,A2,…,Ak-1}⊆Lk-1，但不是D′中的频繁项集，即{A1,A2,…,Ak-1}⊄Lk-1′，那么，D中子集包含{A1,A2,…,Ak-1}的频繁k项集均不在D′的频繁k项集中。

性质4 {A1,A2,…,Ak}是原始数据库D中的频繁k项集，即{A1,A2,…,Ak}⊆Lk，在数据库D′中不为频繁项集，当且仅当{A1,A2,…,Ak}.supportD′

性质5k项集{A1,A2,…,Ak}在原始数据库D中不是频繁k项集，{A1,A2,…,Ak}.supportd+≥c×d+是{A1,A2,…,Ak}在数据库D′中为频繁k项集的必要不充分条件。

性质6A.supportD′=A.supportD+A.supportD+

下面将在BRRPH算法的基础上，利用上述原理，在算法中加入增量更新模型，提高在增量更新情况下的隐私保护挖掘效率。

2.3.2 IBRRPH算法

本文的IBRRPH算法是一个具有隐私保护机制特性的考虑增量更新的频繁模式挖掘算法。IBRRPH算法的第一步即需要将新增的部分数据库进行隐藏和变换；然后在经过了隐私保护的数据集上进行数据挖掘，计算得到候选项集的支持度之后，结合分治策略和逆矩阵的方法求出该候选项集在原始数据库中估计的支持度；最后，得到新的数据库中的频繁项集，因此在IBRRPH算法中，增量之后的数据库的支持度的值为该项集在原始数据库中的支持度与新增数据库的支持度之和，即X.supportD′=X.supportD+X.supportD+。

在IBRRPH算法中，supportD=d×c,supportD+=d+×c,supportD′= (d+d+)×c。

如果A.supportD+≥d+×c，即A在小数据库d+中为频繁项集，当A∈L，那么A.supportD≥d×c，则A为频繁项集。当A∉L，需要重新计算A.supportD+A.supportD+，看是否满足A.supportD+A.supportD+≥supportD′。

如果A.supportD+

根据上述结论可得出增量访问关系如表3所示。本文将此关系应用于增量隐私保护数据挖掘算法中，以达到在利用之前挖掘结果的基础上加速挖掘过程的目的。

表3 增量访问关系

2.4 IBRRPH算法描述

输入：1)D，表示原始数据库； 2)Lk，表示D中的k频繁项集，k=1,2，…r； 3)D+，表示新增数据库； 4)s，表示最小支持度。

输出：L′，表示所有频繁项集。

1)根据文献[9]算法对D+中的数据变换和隐藏，利用bitmap转换规则将扭曲之后的数据转换为bitmap文件。

2)生成L1′，即数据库D+D+的频繁1项集，k=1。在这个过程中，原始数据库D中的频繁1项集是已知的。挖掘频繁1项集的具体过程如算法1所示。

算法1 Mining 1-itemsets of databaseD′。

M=L1;C=∅;L1=∅;Q=∅;

for allt∈D+do

for all 1-itemsetA⊆L1do{

ifA∈MthenA.supportD+++;

else{

//将A加入候选项集C中，并初始化支持度计数

ifA∉Cthen {C=C∪{A};A.supportD+=0;}

A.supportD+++;}

}

for allA∈Mdo

if getTureSupport(A,A.supportD+D+)≥c×(d+d+)

thenL1′=L1′∪{A}

for allA∈Cdo

//修剪C中的项集

if getTureSupport(A,A.supportD+)

then {C=C-{A};Q=Q∪{A}}

for allt∈Ddo

for all 1-itemsetA⊆tdo {

ifA∈CthenA.supportD++;

ifA∈Pthen removeAfromt;

}

for allA∈Cdo

ifA.supportD+D+≥c×(d+d+)

thenL1′=L1′∪{A};

returnL1′;

//getTureSupport(A,num)方法为获取项集A的真实支持度

3)对于k=2,3,…,n,重复以下过程，生成Lk′，直到Lk′=null或者D+=∅。在此过程中，原始数据库D中的频繁k-1项集Lk-1，候选k项集Ck等是已知的。频繁k项集的挖掘过程如算法2所示。

算法2 Miningk-itemsets of databaseD′。

M=Lk;Lk′=∅;

C=brrph-gen(Lk-1′)-Lk;

for allk-itemsetA∈Mdo

for all (k-1)-itemsetB∈Lk-1-Lk-1′ do

ifB⊆A

then {M=M-{A};break;}

for allt∈D+do{

for allA∈getSub(M,t) doA.supportD+++;

for allA∈getSub(C,t) doA.supportD+++;

reduce_db(t);

}

for allA∈Mdo

if getTureSupport(A,A.supportD+D+)≥c×(d+d+)

thenLk′=Lk′∪{A};

for allA∈Cdo{

if getTureSupport(A,A.supportD+)

thenC=C-{A};

reduce_db(t);

}

for allt∈Ddo{

for allA∈getSub(C,t) doA.supportD++;

reduce_db(t);

}

for allA∈Cdo

if getTureSupport(A,A.supportD+D+)≥c×(d+d+)

thenLk′=Lk′∪{A};

returnLk′;

//getSub(M,t)返回t中所有包含M中任一项的子集。

//reduce_db(t);删除db或DB中一些在下一次迭代中

//不需要的项目

2.5 IBRRPH算法挖掘准确度分析

增量式隐私保护数据挖掘与普通隐私保护数据挖掘算法的不同之处主要在于利用了之前的挖掘结果。IBRRPH算法对增量数据集的挖掘，主要是利用了FUP算法的性质，得到加入增量之后的挖掘结果。

在挖掘结果的准确度方面，IBRRPH算法分别分析原始数据集与增量数据集的频繁项集，在算法过程中考虑了其所有可能的情况，根据表3的分析，在原始库和增量库中都不是频繁项集的项集也不可能是全局频繁项集，因此，本文算法在挖掘结果上与原BRRPH算法是等价的。

3 实验结果与分析

本文算法实验平台为：Intel Core i5- 4460 CPU 3.2 GHz处理器和4 GB内存,Windows 7操作系统,开发软件为eclipse 4.3。实验中对于文献[9]算法、BRRPH、IBRRPH等算法进行了实现和性能测试。实验所用的数据全部由IBM Quest Market-Basket Synthetic Data Generator生成。本文所做实验基于T10I4D100KN100等数据集。

3.1 BRRPH算法实验与分析

3.1.1 性能分析

本节选取的参数为p1=p,p2=p3=(1-p1)/2，而p的取值分布于0.1～0.9。

图3为BRRPH算法与文献[9]算法的基于T10I4D100KN100数据集的运行时间对比。原始数据库以参数为p1,p2,p3的概率进行干扰，其中p1=0.6,p2=0.2,p3=0.2，最小支持度为3%。

图3表明，两个算法随着项集个数的增加，运行时间均呈递增趋势。当n<5时，由于两个算法消耗的时间均比较少，BRRPH算法的优势不明显；随着n的增加，BRRPH算法相对于文献[9]算法在效率上的优越性越来越明显。实验结果表明，与文献[9]算法相比，BRRPH算法在效率上有了很大幅度的提高。

图3 两种算法在不同项集个数时的运行时间

数据集的总数分别取50×103,75×103,100×103,125×103，150×103,175×103,200×103,225×103,250×103,275×103，得到频繁5-项集所需时间对比如图4所示。

通过图4可以得知，随着事务个数的增加，与文献[9]算法相比，BRRPH算法在效率上有了很大幅度的提高。由于BRRPH算法添加了将数据库转化为bitmap文件的过程，在数据规模较小时,BRRPH算法的优势较不明显；而随着数据规模的增长，BRRPH算法相对于文献[9]算法优势明显。

3.1.2 准确性分析

本实验将从支持度误差和频繁项集误差两个方面来分析算法的准确性。

图5给出在c=3%时，BRRPH算法和文献[9]算法的项集误差随随机参数p的变化曲线。图6给出p1=0.6,p2=0.2,p3=0.2时，BRRPH算法和文献[9]算法的项集的支持度误差随着最小支持度阈值c的变化曲线。

由图5～6分析可知，在算法参数没有差异的情况下，BRRPH算法相比文献[9]算法，在项集误差和支持度误差上没有明显下降。

图5 两种算法在不同随机参数p时的项集误差

图6 两种算法在不同最小支持度阈值时的支持度误差

3.2 IBRRPH算法实验与分析

下面本文从保持支持度相同逐渐增加增量的角度和保持增量相同支持度不同的角度分别进行了文献[9]算法和本文IBRRPH算法的性能测试，测试结果如图7所示。

图7 两种算法不同增量和支持度时的性能对比

由图7可知：

1)对于一定量的增量数据库，IBRRPH算法相对于文献[9]算法具有较高的效率。

2)支持度小于0.875时,IBRRPH算法的效率提高比较明显(纵轴是算法运行时间,越低越好);而支持度大于0.875时，本文IBRRPH算法耗时稍多于文献[9]算法。

3)因为处理增量数据库的时间越来越多，IBRRPH算法的优越性随着增量数据库规模的增大越来越不明显。

4 结语

针对隐私保护的频繁模式挖掘算法效率问题，通过引入基于bitmap技术和增量更新模型，本文提出了高效的隐私保护的频繁模式挖掘新算法IBRRPH。引入bitmap技术将数据处理转换为位与操作的模式，提高了算法的效率，然后以此为基础，加入增量更新模型，使得算法在数据库发生变化时具有更高效率。实验结果表明，改进之后的算法BRRPH和IBRRPH相比文献[9]的算法在效率上有了较大的提高。由于大数据本身多样的数据类型和快速的数据流转等特征，进一步的研究工作可以从以下几个方面开展：如研究针对非布尔类型数据库上的隐私保护挖掘算法以及研究数据水平式分布和数据垂直式分布的隐私保护的关联规则挖掘算法等。

References)

[1] 王鑫,刘方爱.改进的多数据流协同频繁项集挖掘算法[J].计算机应用,2016,36(7):1988-1992.(WANG X, LIU F A. Improved algorithm for mining collaborative frequent itemsets in multiple data streams [J]. Journal of Computer Applications, 2016, 36(7): 1988-1992.).

[2] 宋健,许国艳,夭荣朋.基于差分隐私的数据匿名化隐私保护方法[J].计算机应用,2016,36,(10):2753-2757.(SONG J, XU G Y, YAO R P. Anonymized data privacy protection method based on differential privacy [J]. Journal of Computer Applications, 2016, 36 (10): 2753-2757.)

[3] 冯登国,张敏,李昊.大数据安全与隐私保护[J].计算机学报,2014,37(1):246-255.(FENG D G, ZHANG M, LI H. Big data security and privacy protection [J]. Chinese Journal of Computers, 2014, 37(1): 246-255.)

[4] SHI H Y, JIANG C, DAI W R, et al. Secure Multi-Party Computation Grid Logistic Regression (SMAC-GLORE) [J]. BMC Medical Informatics and Decision Making, 2016, 16(3): 89.

[5] CHANG X Y, DENG D L, YUAN X X, et al. Experimental realization of an entanglement access network and secure multi-party computation [J]. Scientific Reports, 2016, 6: article no. 29453.

[6] BATMAZ Z, POLAT H. Randomization-based privacy-preserving frameworks for collaborative filtering [J]. Procedia Computer Science, 2016, 96: 33-42.

[7] 方炜炜，谢伟，黄宏博,等.基于隐私保护的序列模式挖掘[J].计算机科学,2016,43(12):195-199.(FANG W W, XIE W, HUANG H B, et al. Sequential pattern mining based on privacy preserving [J]. Computer Science, 2016, 43(12): 195-199.)

[8] 张鹏,童云海,唐世渭,等.一种有效的隐私保护关联规则挖掘方法[J].软件学报,2006,17(8):1764-1774.(ZHANG P, TONG Y H, TANG S W, et al. An effective method for privacy preserving association rule mining [J]. Journal of Software, 2006, 17(8): 1764-1774.)

[9] 顾铖,朱保平,张金康.一种改进的隐私保护关联规则挖掘算法[J].南京航空航天大学学报,2015,47(1):119-124.(GU C, ZHU B P, ZHANG J K. Improved algorithm of privacy preserving association rule mining [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(1): 119-124.)

[10] 陈辉.一种基于位图计算并行挖掘大数据频繁模式算法[J].小型微型计算机系统,2014,35(7):1599-1603.(CHEN H. Parallel mining frequent patterns in big data based on bitmap computation [J]. Journal of Chinese Computer Systems, 2014, 35(7): 1599-1603.)

[11] 肖晗,黄诚.基于量化关联规则的敏感性分析[J].计算机应用,2017,37(S1):255-257.(XIAO H, HUANG C. Analysis of sensitivity based on quantitative association rules [J]. Journal of Computer Applications, 2017, 37(S1): 255-257.)

[12] CHEUNG D W, HAN J W, NG V T, et al. Maintenance of discovered association rules in large databases: an incremental updating technique [C]// Proceedings of the 12th International Conference on Data Engineering. Piscataway, NJ: IEEE, 1996: 106-114.

This work is partially supported by the National Natural Science Foundation of China (61572019), the Key Project of Shaanxi Scientific Research Program (2016JZ001), the Key Laboratory Research Project of Education Bureau of Shaanxi Province (16JS078).

ZHANGYaling, born in 1966, Ph. D., professor. Her research interests include privacy-preserving, data mining.

WANGTing, born in 1990, M. S. candidate. Her research interests include privacy-preserving, data mining.

WANGShangping, born in 1963, Ph. D., professor. His research interests include cryptographic theory, privacy-preserving.