不完备邻域粗糙集的不确定性度量和属性约简

姚 晟，汪 杰，徐 风，陈 菊

(1.安徽大学 计算智能与信号处理教育部重点实验室，合肥 230601； 2.安徽大学 计算机科学与技术学院，合肥 230601)(*通信作者电子邮箱wangjiechn@126.com)

0 引言

粗糙集理论是Pawlak[1]在1982年提出的用于处理不精确和不确定性问题的一种数据分析理论，目前已经广泛应用于模式识别、机器学习、数据挖掘、属性约简和图像分割等研究领域[2-5]。

经典粗糙集理论基于等价关系，它适用于处理符号型数据。然而在现实应用中，数值型属性以及数值型和符号型属性并存的混合数据是普遍存在的，面对这类问题研究人员通常是将数值型数据进行离散化处理[6]，这一转换必然会丢失某些信息。Lin[7]提出了邻域模型的相关概念。邻域粗糙集模型通过定义邻域关系来粒化论域，可以直接处理数值型数据，避免了离散化数据带来的某些损失[8]。

属性约简是粗糙集理论中一种基本的数据预处理技术，目的是剔除无关的冗余属性来保持原有信息系统或者决策表的分类能力。作为粗糙集领域中一项重要的研究内容，目前已经得到大量科研人员的研究与探讨[9-10]。Hu等[11]将信息论中的互信息引入邻域粗糙集模型中，提出了以互信息为启发式函数的属性约简算法，该方法可以处理数值型数据。Chen等[12]在2014年提出了一种基于邻域熵的决策表约简，适用于处理完备信息系统中的数值型数据。然而以上方法都只能处理完备的信息系统，却无法直接处理不完备的信息系统或者具有混合属性的信息系统。

在现实情况中，由于数据获取和数据测量等方面的限制，不完备数据广泛存在，因此，近些年来，研究不完备的信息系统成为热点[13-16]。Wang等[17]提出数据驱动的模型可以用来处理不完备的符号型数据，但是却不能处理数值型数据。姚晟等[18]提出邻域量化容差关系用来处理不完备的数值型数据，却不能处理不完备的符号型数据。为了同时处理混合型数据，何松华等[19]提出了邻域组合测度的属性约简方法。然而，在邻域组合测度方法中，计算对象之间的距离时认为当属性值存在缺失时两者之间的距离为0，这种数据之间关系的刻画显然较为宽松，没有考虑数据分布特征，存在一定的缺陷。

为克服对象缺失属性值之间距离刻画过于宽松的缺陷，本文提出了一种拓展不完备邻域粗糙集模型，考虑了属性值的分布情况，利用统计学中的方法求出所有已知属性值的频率，将该频率作为该对象取该属性值的概率。当某个已知属性值的概率越大，某对象的未知属性值与其相等的可能性就越大，此时两个对象在当前属性下的距离为0；相反，概率越小，未知属性值与其相等的可能性就越小，此时距离为1。这种方式考虑了数据的分布特征，因此更具有客观性，并在此基础上结合启发式信息定义了邻域混合熵的概念来评价所选属性的质量。最后根据邻域混合熵提出基于邻域混合熵的不完备邻域粗糙集属性约简(Attribute Reduction of Neighborhood Mixed Entropy, ARNME)算法。该算法不仅可以处理混合数据，而且适用于不完备信息系统。实验结果表明，本文算法能够获得较少的约简属性和较高的分类精度。

1 背景知识

下面简单介绍经典粗糙集和邻域粗糙集的相关性质。

1.1 经典粗糙集

在粗糙集理论中，知识被认为是分辨对象的能力，并采用等价关系将论域粒化为若干等价类，利用上下近似逼近的方式刻画未知概念，通过知识约简来发现数据当中潜在的知识和规律[1]。

其中，本文中所有|U|均表示论域U的基数。当属性值存在缺失时，DT就叫作不完备决策信息系统或不完备决策表。本文中所有“*”均表示属性值缺失的情形。

定义2[1]设DT=(U,A,V,f)，对于任意条件属性子集B⊆C，B上的不可分辨关系定义为：

IND(B)={(x,y)∈U×U|∀a∈B,

f(x,a)=f(y,a)}

(1)

定义3[1]设DT=(U,A,V,f)，对于任意条件属性子集B⊆C，论域上的一个对象子集X⊆U，定义X在条件属性子集B上的下近似、上近似和边界域分别为：

(2)

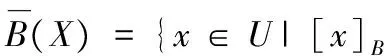
(3)

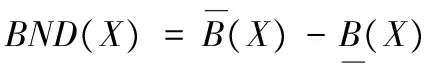
(4)

其中：[x]B是x在条件属性集B上的等价类。

1.2 邻域粗糙集及其相关性质

定义4[8]给定一个邻域决策系统NDT=(U,C,D)。条件属性集B={b1,b2,…,bm}，对∀x1,x2,x3∈U，Δ满足:

1)ΔB(x1,x2)≥0,ΔB(x1,x2)=0当且仅当x1=x2;

2)ΔB(x1,x2)=ΔB(x2,x1);

3)ΔB(x1,x3)≤ΔB(x1,x2)+ΔB(x2,x3)

ΔB(x1,x2)表示对象x1和对象x2之间的距离。目前常用的距离函数有曼哈顿距离、欧氏距离和切比雪夫距离。

欧氏距离定义为：

(5)

定义5[8]给定一个邻域决策系统NDT=(U,C,D)和B⊆C。对于U中任意对象xi，定义其关于B的δ邻域为：

δ(xi)={x∈U|ΔB(x,xi)≤δ}

(6)

其中，δ≥0，Δ为距离函数。

定义6[8]给定一个邻域决策系统NDT=(U,C,D)以及B⊆C。∀X⊆U，定义X关于条件属性的下近似、上近似和边界域分别为：

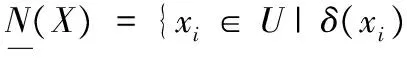
(7)

(8)

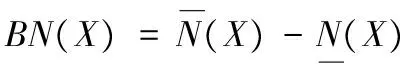
(9)

2 不完备邻域粗糙集的不确定性度量

2.1 不完备邻域粗糙集模型

为了处理不完备的混合属性数据，本文在对数值型属性和符号型属性进行距离度量时均考虑用数据的概率分布来构建距离公式。

对符号型属性，求出所有已知属性值的频率作为该属性值出现的概率，继而得出所有已知属性值的概率分布。假设一对象x在b属性下取值为非空且该属性值出现的概率为p，另一对象y在b属性下取值为空，则y对象在b下取值与x取值相等的可能性为p，此时对象x,y在b下的距离为0,因此可预先设定一个阈值，当p大于等于该阈值时，对象x,y在b下的距离为0，否则距离为1。当对象x,y在b属性下取值都为空的情况下，则两者属性值可能取每一个非空属性值，计算距离时需要考虑取每一个非空属性值的概率。

针对数值型属性，由于其属性值取值是具体的数值，无法通过直接计算属性值出现的频率来度量两个对象在某一属性下属性值存在缺失时取相同属性值的概率，因此可将属性值的邻域包含的数目作为这个属性值出现的频率，从而得出该属性值出现的概率分布。

定义7 给定一个邻域决策系统NDT=(U,C,D)和一个混合属性集合B⊆C，且B={b1,b2,…,bn}。对∀x,y∈U,距离函数定义为：

(10)

且∀bl∈B，距离的度量分为两种情况。

1)当bl为数值型属性,预先设定一个阈值λ1和邻域半径δ。当对象x在属性bl下属性值非空时，记nbl(x)为对象x关于属性bl的邻域类，且满足nbl(x)={y∈U|NPbl(x,y)≤δ∧bl(y)≠*},其中：kbl={x∈U|bl(x)≠*}为属性bl下的非空对象集，|·|为集合的基数。

则数值型属性距离公式定义为：

NPbl(x,y)=

(11)

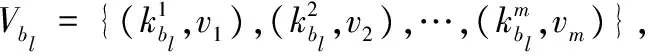
NPbl(x,y)=

(12)

定义8 给定一个邻域决策系统NDT=(U,C,D),B1⊆C是一个数值型属性集合，B2⊆C是一个符号型属性集合，B=B1∪B2是一个混合属性集合，邻域半径为δ。∀xi∈U，其在混合属性B下的邻域类定义为：

(13)

其中：

nB1(xi)={x∈U|NPB1(x,xi)≤δ}

(14)

nB2(xi)={x∈U|NPB2(x,xi)=0}

(15)

定理1 给定一个邻域决策系统NDT=(U,C,D),M,N⊆C和邻域半径为δ。∀xi∈U，有：

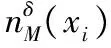
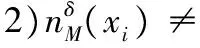
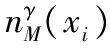
证明 1)由题设可知M⊆N，设N=N1∪N2，M=M1∪M2。其中N1,M1为数值型属性集合，N2,M2为符号型属性集合。

由定义8可知：

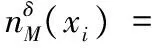
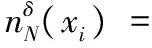
{x∈U|NPN1(x,xi)≤δ}∧{x∈U|NPN2(x,xi)=0}

又因为M1⊆N1,M2⊆N2，由此可得：NPM1(x,xi)≤NPN1(x,xi),NPM2(x,xi)≤NPN2(x,xi)。

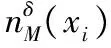
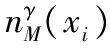
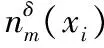
定义9 给定一个邻域决策系统NDT=(U,C,D)和属性集B⊆C。∀X⊆U，X关于B的下近似和上近似分别为：

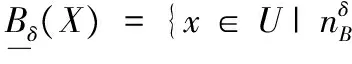
(16)

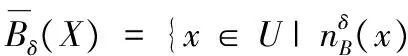
(17)

定义10 给定一个邻域决策系统NDT=(U,C,D)和属性集B⊆C。∀B⊆C，X关于条件属性集B的依赖度定义为：

(18)

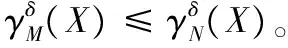
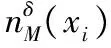
定义11 给定一个邻域决策系统NDT=(U,C,D)和属性集B⊆C，其中U/IND(D)={D1,D2,…,Di}是论域U在决策属性D下的等价类。决策属性D关于条件属性B的依赖度定义为：

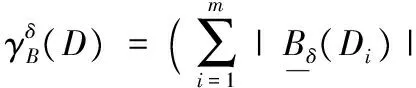
(19)

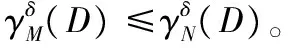
证明 根据定理2可得。

2.2 实例分析

例1 给定一个邻域决策系统NDT=(U,C,D)如表1所示。其中，条件属性集C={a,b,c,d,e}，决策属性为D，且{a,b,c}为数值型属性，{d,e}为符号型属性，且λ1=λ2=0.5,δ=0.1。

求对象x1的邻域类中是否包含对象x2。

①x2在数值型属性c下属性值缺失，根据式(11)，x1,x2在属性c下在同一邻域类的概率p1=3/4。

因为p1≥λ1，所以对象x1,x2在c下的距离为0。

②x1在符号型属性e下属性值缺失，根据式(12)，x1,x2在属性e下取值相等的概率p2=1/2。

因为p2≥λ2，所以对象x1,x2在e下的距离为0。

③同理根据定义7求得对象x1,x2的距离为

NPC(x1,x2)=0.1≤δ

所以对象x2对象x1的邻域类中。

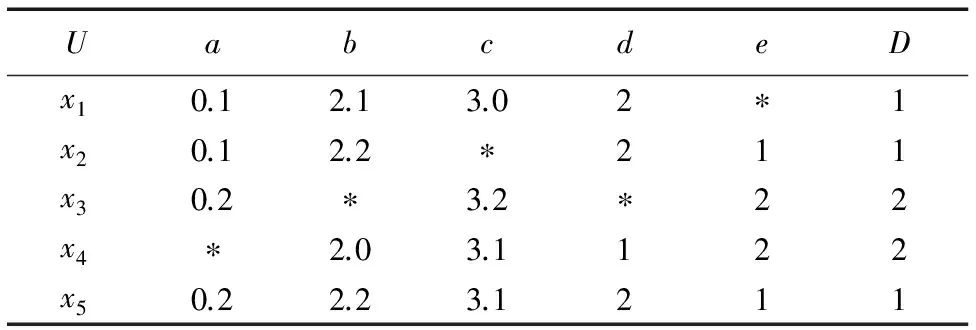
表1 决策表S

2.3 邻域混合熵及其相关性质

目前常用来评价属性约简质量的方法主要有基于代数的方法和基于信息论的方法[9-10]。其中，基于代数的方法判断属性是否是冗余属性的标准是该属性是否对集合中确定分类子集产生影响；基于信息论的方法判断冗余属性的标准是该属性是否对集合中的不确定分类子集产生影响[20]。基于代数的定义和基于信息论的定义具有很强的互补性，近些年来已经得到了广泛的研究[21-23]。本文首先将邻域信息熵应用到不完备混合属性数据的处理中，并结合依赖度提出邻域混合熵的度量方法，通过代数视角和信息论视角来评价属性的重要度。

定义12 给定一个邻域决策系统NDT=(U,C,D)。其中B1⊆C是一个数值型属性集合，B2⊆C是一个符号型属性集合，B=B1∪B2是一个混合属性集合，对应的邻域半径为δ，则关于属性集B的邻域信息熵定义为：

(20)

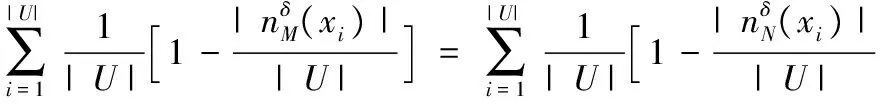
所以Eδ(M)=Eδ(N)。

定理5 给定一个邻域决策系统NDT=(U,C,D)。如果M⊆N⊆C，那么Eδ(M)≤Eδ(N)。

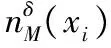
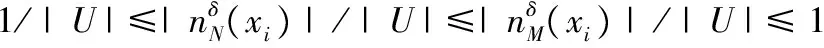
由此可得：Eδ(M)≤Eδ(N)。

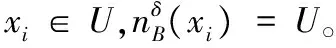
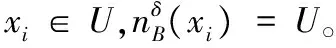
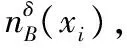
证明 由定理5容易得出。

定义13 给定一个邻域决策系NDT=(U,C,D),B⊆C和X⊆U，则X相对于属性集B的邻域混合熵定义为：

(21)

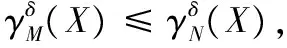
定义14 给定一个邻域决策系统NDT=(U,C,D)，B⊆C和X⊆U，其中U/IND(D)={D1,D2,…,Di}，则决策属性D关于条件属性B的邻域混合熵定义为：

(22)

通常粗糙集的不确定性度量方法应该满足以下三个条件[24]：1)单调性；2)非负性；3)不变性。下面分别给出证明。

证明 根据定理8显然成立。

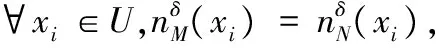
证明 不变性显然成立。

证明 由定理5可得。

定理9～11表明了邻域混合熵具有单调性、非负性和不变性，因此，邻域混合熵可以作为属性约简的评价函数。

定义15 给定一个邻域决策系统NDT=(U,C,D)，其中U/IND(D)={D1,D2,…,Di}。B⊆C和a∈C-B,则a相对于属性集B的重要性定义为：

(23)

定义16 给定一个邻域决策系统NDT=(U,C,D)，其中U/IND(D)={D1,D2,…,Di}。B⊆C为条件属性集C的一个约简，如果B满足：

(24)

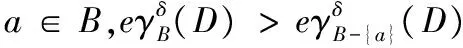
(25)

3 属性约简算法

算法将邻域混合熵作为启发式函数，构造基于邻域混合熵的属性约简算法。算法以空集作为起点，每次计算全部剩余属性的属性重要度，从中选择属性重要度最大的属性加入到约简集中，直到所有剩余条件属性的重要度为0为止，返回约简结果。

算法1 计算邻域混合熵。

输入：邻域决策系统NDT=(U,C,D)，B={B1,B2}。其中，B1⊆C是数值型属性集合，B2⊆C是符号型属性集合。邻域半径为δ，U/IND(D)={D1,D2,…,Dm}。

1)初始化,令Eδ(B)=0;

2)对于每个1≤i≤|U|,循环执行:

①计算xi的邻域类

②计算邻域熵

3)对于每个1≤j≤m,循环执行:

4)计算依赖度

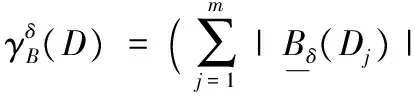
5)计算邻域混合熵

算法2 ARNME算法。

输入：NDT=(U,C,D)；

输出：约简red。

1)初始化,令red=∅;

2)对条件属性集C中任意属性a,计算邻域关系Na;

3)对于任意ai∈C-red,循环执行:

//其中γ∅(D)=0

②选择一个属性ak满足条件:

SIG(ak,red,D)=max{SIG(ai,red,D)};

③计算ak的属性重要度SIG(ak,red,D)。

4) ifSIG(ak,red,D)>0

令red=red∪ak

跳转到3);

else

跳转到5);

5)返回约简red。

4 实验分析

为了验证本文提出的算法对处理不完备混合属性数据的有效性，将分别从以下几点进行实验分析：首先比较本文算法与其他算法的约简结果；然后比较本文算法与对比算法的分类精度。

4.1 实验准备

本文从UCI数据集中选用了7个数据集，包括4个不完备数据集，3个完备数据集，其中4个数据集具有混合属性、2个数据集只有符号型属性、1个数据集只有数值型属性，具体描述如表2。为了在计算邻域时消除量纲的影响，实验所用的所有数值型数据全部被标准化到[0,1]区间；同时，设置邻域半径为δ=0.1，阈值λ1=λ2=0.5。

本实验测试环境为一台i3 3.7 GHz(4 GB内存,Windows 10操作系统)，采用Java语言实现算法。将本文算法与基于依赖度的属性约简(Attribute Reduction of Dependency, ARD)算法[8]、基于邻域条件熵的属性约简(Attribute Reduction of neighborhood Conditional Entropy, ARCE)算法[25]、基于邻域组合测度的属性约简(Attribute Reduction of Neighborhood Combination Measure, ARNCM)算法[19]进行比较。

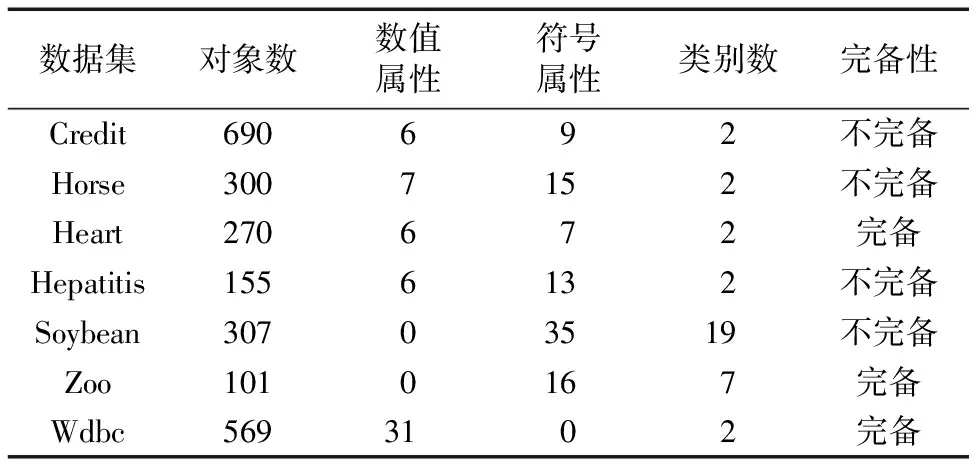
表2 数据集简介

4.2 分类属性数量比较

首先比较不同算法属性约简的情况。表3是4种属性约简算法约简后的属性数量与数据集原始属性数量的比较。从实验的结果可以看出，4种算法都可以约简掉冗余的属性。其中，ARNME算法和ARNCM算法约简后的属性数量接近一致，都能够获得较小的约简结果，在大部分数据集中ARNME算法的属性数量小于ARD算法和ARCE算法。从约简结果的平均数来看，本文的ARNME算法获得的平均属性约简数为9,而ARD、ARCE和ARNCM算法分别为10，17和9，因此从总体来看，本文算法能够获得较少的属性数量。

表3 约简前后属性数比较

4.3 分类精度比较

为了更好地验证算法的有效性，实验引入经典的分类与回归树(Classification and Regression Trees, CART)和支持向量机(Support Vector Machine, SVM)两种分类器，采用十折交叉验证的分类精度来评估所选属性的质量。实验结果如表4所示。

表4是4种约简算法约简后的分类精度和原始精度的比较。通过实验数据可以看出约简后的属性分类精度并没有明显的降低，这说明原始的属性中包含一些冗余属性，这4种约简算法在剔除这些冗余属性后既能够降低属性维度，又能够保有原有的数据信息，因此都适用于属性约简。

观察表4 CART分类器中的数据发现，在大部分数据集中，本文算法的分类精度略高于其他3种对比算法。从单个数据集来看：在Horse和Zoo数据集中，ARNME算法的分类精度略低于ARD算法的分类精度，但是高于ARCE算法的分类精度；在Heart和Wdbc数据集中，ARNME算法比其他对比算法获得较高的分类精度；在Credit数据集中，ARNME算法的分类精度与其他3种对比算法相等；在Soybean数据集中，ARNME算法的分类精度高于其他3种对比算法，说明该算法对具有混合属性的不完备数据的处理有较好的效果。再从分类精度的平均值综合来看，本文算法的平均精度高于原始精度和其他3种算法的分类精度。这说明本文算法在CART分类器下在不降低分类精度的前提下能够获得较好的分类精度。

表4 不同分类器下分类精度比较

通过观察表4 SVM分类器中的数据发现，从单个数据集来看，在Heart数据集中，ARNME算法的分类精度略低于ARNCM算法，但是高于ARD和ARCE算法。在Horse、Hepatitis、Soybean这3种具有混合属性的数据集中，ARNME算法的分类精度高于其他3种对比算法。在Zoo数据集中略低于ARD和ARCE算法，但是高于ARNCM算法。其他的数据集中ARNME算法均获得较高的分类精度。从平均分类精度来看，ARNME算法的平均精度为0.891 6，高于其他3种算法和原始属性的分类精度。这说明ARNME算法在SVM分类器下也能够获得较好的分类精度。

由以上的实验结果可知，本文提出的算法不仅可以处理不完备数据，还可以处理混合属性数据；能够在获得较小约简结果的同时保持较高的分类精度。

5 结语

本文针对符号型属性和数值型属性共同存在的情况，考虑了数据中所隐含的信息，利用已知属性值的概率分布情况构造了拓展不完备邻域粗糙集模型；分析了基于代数和基于信息的启发式函数的优缺点，定义了邻域混合熵的启发式函数，定义和证明了其在不完备邻域信息系统中的相关性质和定理，并提出了基于邻域混合熵的不完备邻域粗糙集属性约简算法。通过实验将该算法与其他算法进行了比较，实验结果表明，本文的算法能够获得较少的约简属性和较高的分类精度。不同的阈值λ1、λ2会影响属性约简个数和分类精度，本文的阈值是通过考察数据的分布特征并结合概率的相关知识给出的，可能不适用于其他数据集，因此具有一定的局限性，接下来的工作是研究如何通过机器学习等方法选择合适的阈值。

References)

[1] PAWLAK Z. Rough sets [J]. International Journal of Computer and Information Sciences, 1982, 11(5): 341-356.

[2] SARAH V, LYNN D, YVAN S, et al. Applications of fuzzy rough set theory in machine learning: a survey [J]. Fundamenta Informaticae, 2015, 142(1/2/3/4): 53-86.

[3] RAHMAN A, MUHAMMAD H S, SUNGYOUNG L. Rough set-based approaches for discretization: a compact review [J]. Artificial Intelligence Review, 2015, 44(2):235-263.

[4] WANG D L, SONG X F, YUAN J Y. Forecasting core business transformation risk using the optimal rough set and the neural network [J]. Journal of Forecasting, 2015, 34(6): 478-491.

[5] CHEN L F, CHIHTSUNG T. Data mining framework based on rough set theory to improve location selection decisions: a case study of a restaurant chain [J].Tourism Management, 2016, 53: 197-206.

[6] JENSEN R, SHEN Q. Semantics-preserving dimensionality reduction: rough and fuzzy-rough-based approaches [J]. IEEE Transactions On Knowledge and Data Engineering, 2004, 16(12): 1457-1471.

[7] LIN T Y. Granular computing on binary relations [C]// RSCTC 2002: Proceedings of the Third International Conference on Rough Sets and Current Trends in Computing. Berlin: Springer, 2002: 296-299.

[8] 胡清华,于达仁,谢宗霞.基于邻域粒化和粗糙逼近的数值属性约简[J].软件学报,2008,19(3):640-649.(HU Q H, YU D R, XIE Z X. Numerical attribute reduction based on neighborhood granulation and rough approximation [J]. Journal of Software, 2008, 19(3): 640-649.)

[9] XIE J, SHEN X F, LIU H F, et al. Research on an incremental attribute reduction based on relative positive region [J]. Journal of Computational Information Systems, 2013, 9(16): 6621-6628.

[10] WANG C R, QU F F. An attribute reduction algorithm in rough set theory based on information entropy [C]// Proceedings of the 2008 International Symposium on Computational Intelligence and Design. Washington, DC: IEEE Computer Society, 2008: 3-6.

[11] HU Q H, ZHANG L, ZHANG D, et al. Measuring relevance between discrete and continuous features based on neighborhood mutual information [J]. Expert Systems with Applications, 2011, 38(9): 10737-10750.

[12] CHEN Y M, WU K S, CHEN X H, et al. An entropy-based uncertainty measurement approach in neighborhood systems [J]. Information Sciences, 2014, 279: 239-250.

[13] DAI J H. Rough set approach to incomplete numerical data [J]. Information Sciences, 2013, 241: 43-57.

[14] LIANG J, SHI Z, LI D, et al. Information entropy, rough entropy and knowledge granulation in incomplete information systems [J]. International Journal of General Systems, 2006, 35(6): 641-654.

[15] QIAN Y H, LIANG J Y, PEDRYCZ W, et al. An efficient accelerator for attribute reduction from incomplete data in rough set framework [J]. Pattern Recognition, 2011, 44(8): 1658-1670.

[16] 罗豪,续欣莹,谢珺,等.基于扩展容差关系的不完备信息系统属性约简[J].计算机应用,2016,36(11):2958-2962.(LUO H, XU X Y, XIE J, et al. Attribute reduction in incomplete information systems based on extended tolerance relation [J]. Journal of Computer Applications, 2016, 36(11): 2958-2962.)

[17] WANG G Y, GUAN L H, WU W Z, et al. Data-driven valued tolerance relation based on the extended rough set [J]. Fundamenta Informaticae, 2014, 132(3): 349-363.

[18] 姚晟,徐风,赵鹏,等.基于邻域量化容差关系粗糙集模型的特征选择算法[J].模式识别与人工智能,2017,30(5):416-428.(YAO S, XU F, ZHAO P, et al. Feature selection algorithm based on neighborhood valued tolerance relation rough set model [J]. Pattern Recognition and Artificial Intelligence, 2017, 30(5): 416-428.)

[19] 何松华,康婵娟,鲁敏，等.基于邻域组合测度的属性约简方法[J].控制与决策,2016,31(7):1225-1230.(HE S H, KANG C J, LU M, et al. Attribute reduction method based on neighborhood combination measure [J]. Control and Decision, 2016, 31(7): 1225-1230.)

[20] 王国胤,于洪,杨大春.基于条件信息熵的决策表约简[J].计算机学报,2002,25(7):759-766.(WANG G Y, YU H, YANG D C. Decision table reduction based on conditional information entropy [J]. Chinese Journal of Computers, 2002, 25(7): 759-766.)

[21] 江峰,王莎莎,杜军威,等.基于近似决策熵的属性约简[J].控制与决策,2015,30(1):65-70.(JIANG F, WANG S S, DU J W, et al. Attribute reduction based on approximation decision entropy [J]. Control and Decision, 2015, 30(1): 65-70.)

[22] 黄国顺,文翰.基于边界域和知识粒度的粗糙集不确定性度量[J].控制与决策,2016,31(6):983-989.(HUANG G S, WEN H. Uncertainty measures of rough sets based on boundary region and knowledge granularity [J]. Control and Decision, 2016, 31(6): 983-989.)

[23] 唐朝辉,陈玉明.邻域系统的不确定性度量方法[J].控制与决策,2014,29(4):691-695.(TANG C H, CHEN Y M. Neighborhood system uncertainty measurement approaches[J]. Control and Decision, 2014, 29(4): 691-695.)

[24] 黄国顺,曾凡智,文翰.基于条件概率的粗糙集不确定性度量[J].控制与决策,2015,30(6):1099-1105.(HUANG G S, ZENG F Z, WEN H. Uncertainty measures of rough set based on conditional possibility [J]. Control and Decision, 2015, 30(6): 1099-1105.)

[25] ZHAO H, QIN K. Mixed feature selection in incomplete decision table [J]. Knowledge-Based Systems, 2014, 57: 181-190.

This work is partially supported by the National Natural Science Foundation of China (61602004, 61300057), the Natural Science Foundation of Anhui Province (1508085MF127), the Key Project of Natural Science Research of Anhui Higher Education Institutions (KJ2016A041), the Public Bidding Project of Co-Innovation Center for Information Supply & Assurance Technology (ADXXBZ2014- 5, ADXXBZ2014- 6), the Doctoral Scientific Research Foundation of Anhui University (J10113190072).

YAOSheng, born in 1979, Ph. D., lecturer. Her research interests include rough set, granular computing, big data.

WANGJie, born in 1993, M. S. candidate. His research interests include rough set.

XUFeng, born in 1993, M. S. candidate. His research interests include rough set.

CHENJu, born in 1993, M. S. candidate. Her research interests include rough set.