基于单计算单元的极化码CA-SCL译码器FPGA设计∗

魏一鸣 仰枫帆

（南京航空航天大学电子信息工程学院 南京 211106）

1 引言

极化码［1］是一种基于信道极化现象的信道编码，是由土耳其教授Erdal Arikan在2007年首次提出，并指出其为当下唯一可理论证明达到香农极限［2］的信道编码，且具有较低的编译码复杂度，由此学术界掀起了极化码的研究热潮。随后，在Ari⁃kan的SC译码算法［1］的基础上，有学者对其进行了改进，提出了 SCL［3］、CA-SCL［4］等译码算法，尤其是CA-SCL译码算法，获得了优于最大似然算法的性能［5］。与此同时，为了探寻极化码工程上实现的可能性，众多学者开始致力于极化码硬件实现并开始提出了一些SC译码硬件结构［6～10］。而其中的半并行结构［8］仅以较小的吞吐量为代价，大幅减小了系统面积，在后续提出的 SCL［11～12］、CA-SCL［13］硬件结构中也均采用此结构。作为性能最好的CA-SCL译码算法，列表宽度L很大程度上制约了该算法的性能，而随着L的增大，在半并行结构下的系统资源将被大量消耗。本文所采用的单计算单元架构使整个系统的计算单元保持为L个，即每条候选路径仅对应一个计算单元，大大减少了系统面积。为了弥补此设计对吞吐率造成的影响，核心译码模块采用流水线技术，提高了系统工作频率。

2 信道极化现象

Arikan在研究信道的组合和拆分的过程中发现［14～15］，在将 N 个相互独立的信道进行组合和拆分后，系统的总体容量没有发生改变，而总体截止速率得到了提升。基于此研究，Arikan将N个相互独立的完全相同的二进制离散无记忆（B-DMC）信道通过组合合并为信道WN，并将WN拆分为N个相关子信道∶1≤i≤N }，随着 N 的不断变大，其子信道容量)}趋向0或1两个极端，此现象便被称为信道极化现象，过程如图1所示。通常地，我们使用信道容量趋向1的子信道传送信息比特，而使用信道容量趋向0的子信道传送收发双方均已知的固定比特，其默认值为0。

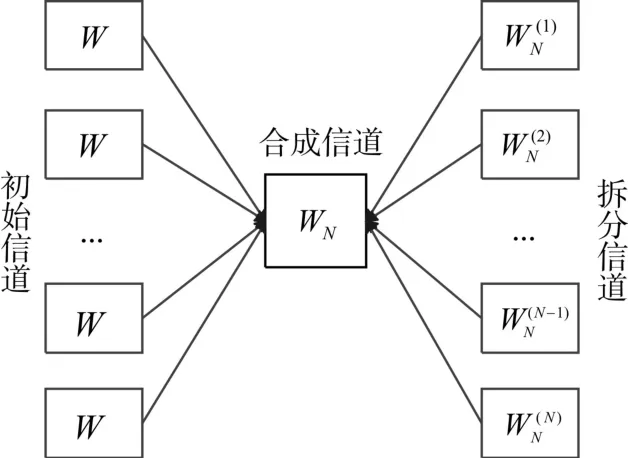
图1 信道极化过程

如何挑选信道非常重要，在学者们的不断研究中涌现了许多高性能的信道挑选方法［16～18］。Arikan指出，通常情况下对于任意信道都可以使用BEC信道下的信道挑选方法而不会产生较大的性能损失［1］，通常令初始信道容量为 I(=0.5，使用如下迭代公式进行信道挑选：

3 极化码的编译码算法

3.1 极化码编码方法

极化码作为一种线性分组码，其码字的产生同样需要一个生成矩阵：，其中为经过信道挑选并混入固定比特的初始信息，为生成的码字。根据信道的组合方法［1］可以迭代地得到生成矩阵GN=其中 F为核矩阵F⊗n为 F 的 n阶Kronecker积［1］，n=log2N 。 BN为比特反转操作：令xi=Vπ(i)，其中x的下标i的二进制 表 示 为 (b1b2…bn)， 转 换 关 系 为i=·2n-k)+1。经过比特反转操作 π后，π(i)的二进制表示为(bnbn-1…b1)。

3.2 极化码CA-SCL译码算法

极化码发展至今已有多种译码方法，其中CA-SCL译码算法性能最佳，且具有较低的译码复杂度。由于CA-SCL算法是在SCL算法的基础上添加CRC检验位［19］以提高译码性能，所以该算法也可以说由三部分组成。

3.2.1 SC译码算法部分

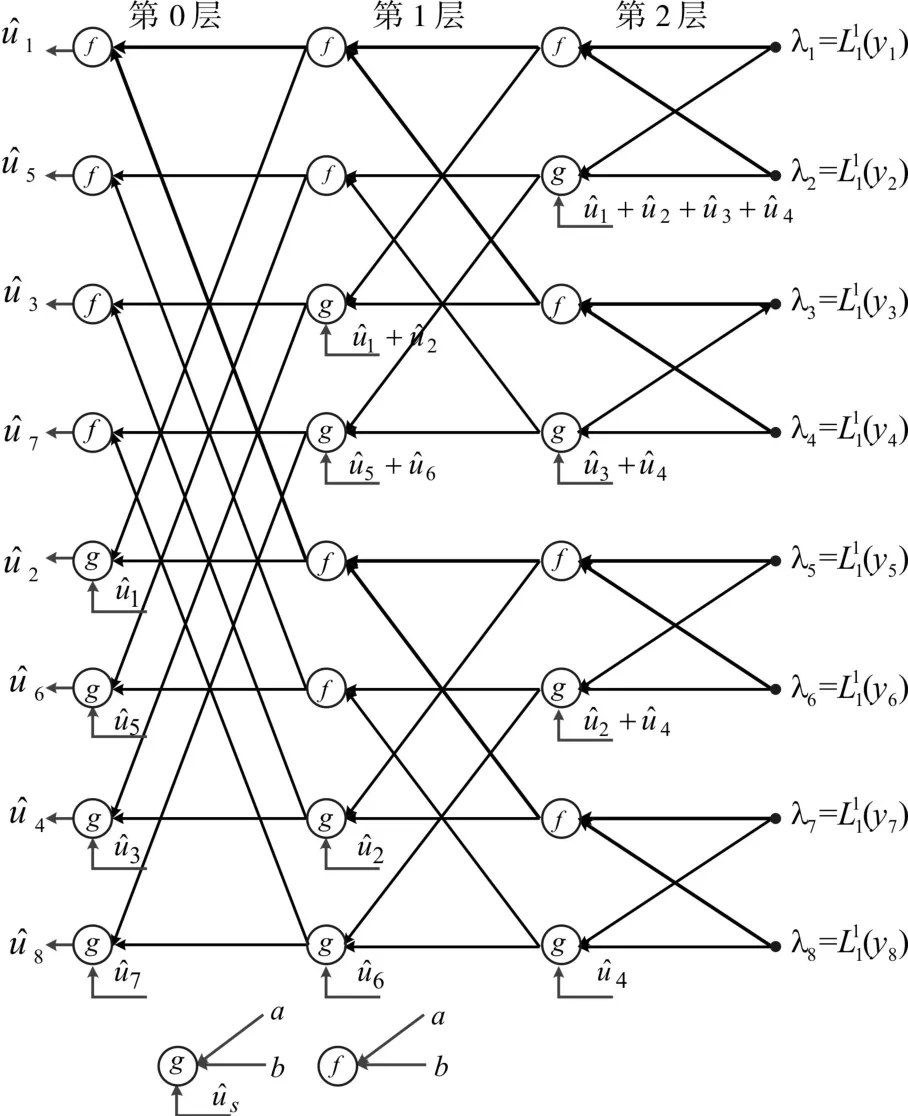
图2 L=8时SC译码流程

图中，f节点和g节点的计算公式使用最小和算法［6，22］表示为

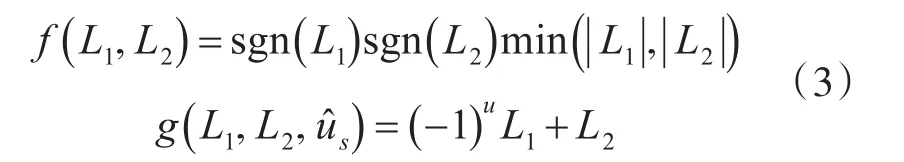
该算法仅含有加减运算，适合用于硬件实现。其中u^s为已经译出的码字的部分和。在硬件实现中往往将两者融合为一个节点，被称为一个计算单元（Processing Element，PE），并通过复用器来实现二者的功能转换。

3.2.2 SCL译码算法部分

在SC译码算法中，每个阶段仅存在一条候选路径，错误极易累加。所以在SCL译码算法［3］中，每个译码阶段都存在路径度量值较大的L( )L≥2条候选路径，而最终目的即为从这L条路径中选出最佳路径。与SC译码算法中对当前比特直接判决不同，SCL算法中每一个比特在译码过程中的顶层按如下公式进行路径度量值PM的计算［13］：

初始列表中只有一条空路径，且PM(ϕ)=0。我们可以将此过程表述为一个深度为N的满二叉树，一个N=4，L=2的译码过程如图2所示，图中的数字为当前阶段的路径度量值PM。

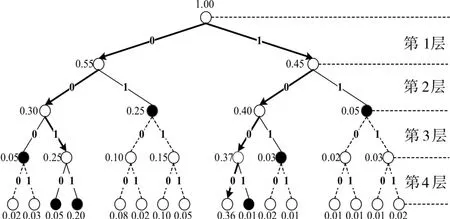
图3 N=4，L=2SCL译码码树图

3.2.3 CRC校验部分

假设编码器输入为k比特的信息位，然后添加m位CRC码，使得编码器的输入为K=k+m比特，对此K比特的信息位进行极化码编码，得到N位信道输入，经过信道传输后送入CA-SCL译码器进行译码。当SCL译码器译出L个候选序列之后，将此L个序列对应的路径度量值进行由大到小排序，并以此顺序依次进入解CRC码单元。当译出的序列不满足CRC关系时，该单元将告知SCL译码器，继续传送下一个序列。就这样直到输入解CRC码单元的序列通过CRC校验，译码结束，解除CRC校验码，得到的输出序列即为CA-SCL译码器译出的码字。

4 CA-SCL译码器硬件结构设计

4.1 译码器整体结构设计

在本次的译码器设计中，码长为1024，码率为1/2，信道挑选方法为BEC方法，列表宽度L=32，采用LTE协议建议的24位CRC检验码，其生成多项式为g(D)=D24+D23+D18+D17+D14+D11+D10+D7+D6+D5+D4+D3+D+1。对译码器中的数据进行8比特量化，路径度量值进行12比特量化，对译码过程中发生的溢出采用截断处理，使得位宽不会逐级递增，大大简化了译码器的设计复杂度，且只有极小的性能损失。整体结构主要包括以下几个顶层模块：LLR计算模块（LLR_top）、修正模块（Corrected）、度量值计算模块（Metric_top）、度量值排序模块（Sort_top）、反馈模块（Feedback）、控制模块（Controller）路径恢复模块（Path_recover）、CRC串行译码模块（CRC），如图4所示。在译码开始之前，首先将信道LLR两两分组，存入位宽为16，深度为512的RAM中作为初始LLR，即图中的LLR_based RAM。

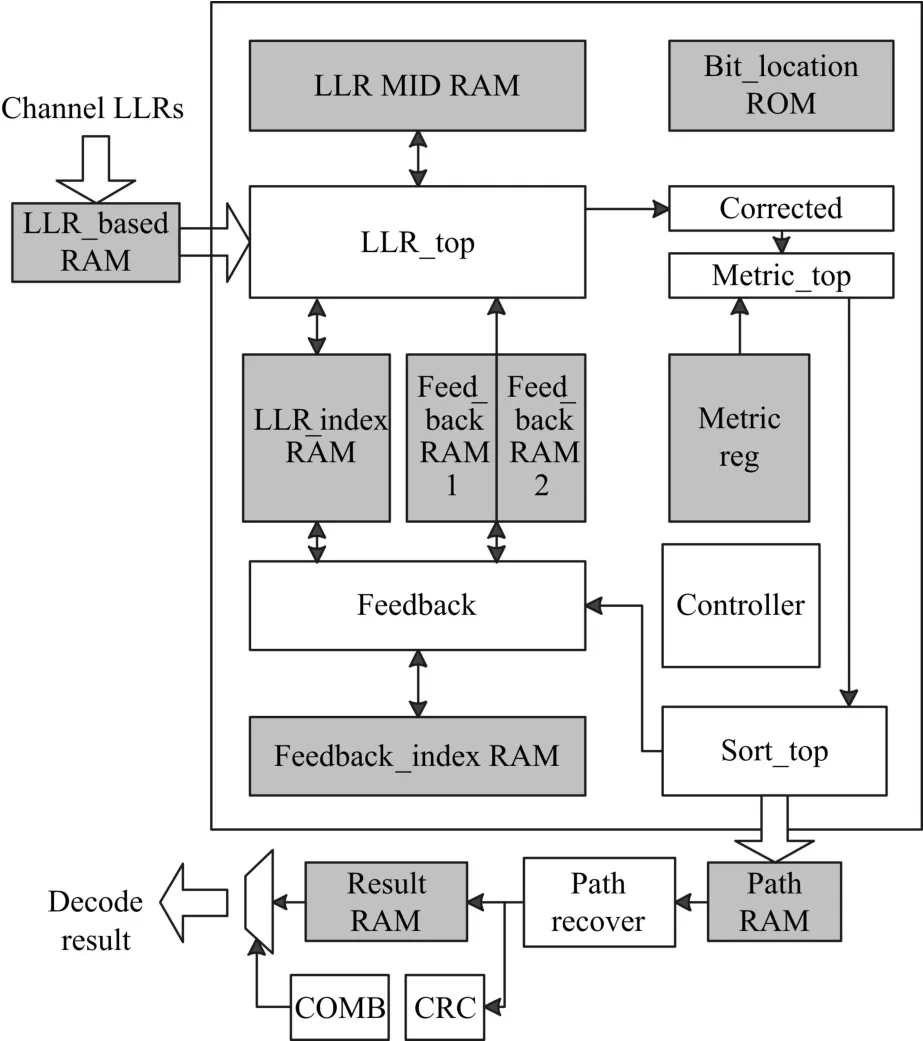
图4 译码器整体结构

4.2 LLR计算模块

模块的整体结构如图5所示，由LLR控制单元和计算单元组成。如图2所示在单次顶层LLR的计算中，每一层都仅激活 f或g节点中的一种，所以令总控制模块生成位宽为10的状态寄存器IDX，最低位对应顶层，最高位对应信道层，IDX(i)=0表示第i层处于工作状态的是 f节点，否则为g节点。当计算下一比特对应的顶层LLR时，在时钟的控制下令IDX加1，即可进入当前状态。译码开始时，在IDX的控制下读取信道LLR，将计算后的结果存于中间值存储器LLR MID RAM中。当读地址到达512，表示信道LLR读取完毕，开始读中间值，由此不断计算，直到得出顶层LLR的值。

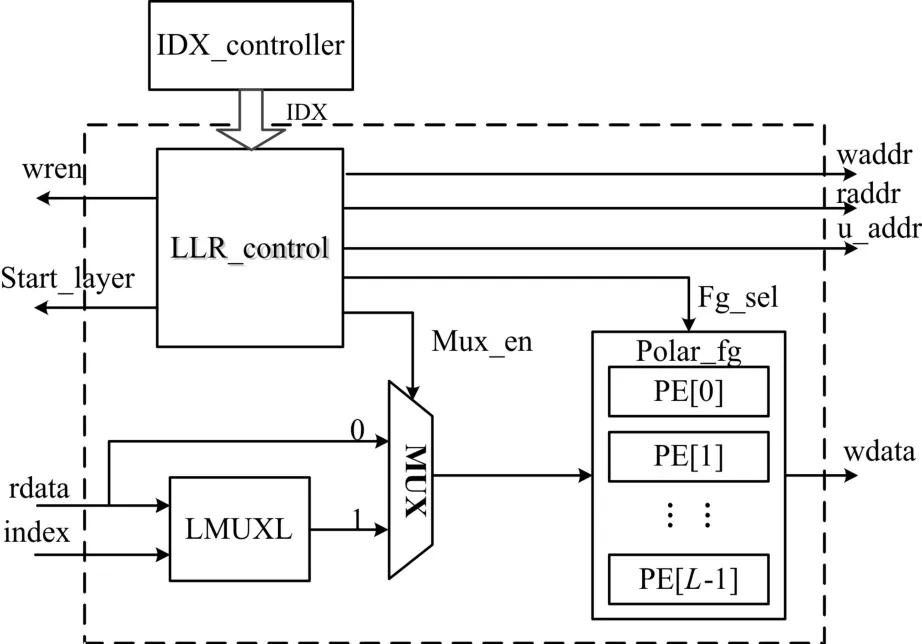
图5 LLR计算模块硬件结构

由于本设计采用单计算单元架构，所以针对每一条路径都仅使用1个PE进行相应的LLR计算。本文设计的系统中，32个PE处于并行处理状态，即同时处理来自不同路径的计算请求，最终同时计算得到顶层LLR。单个PE的硬件结构如图6所示。

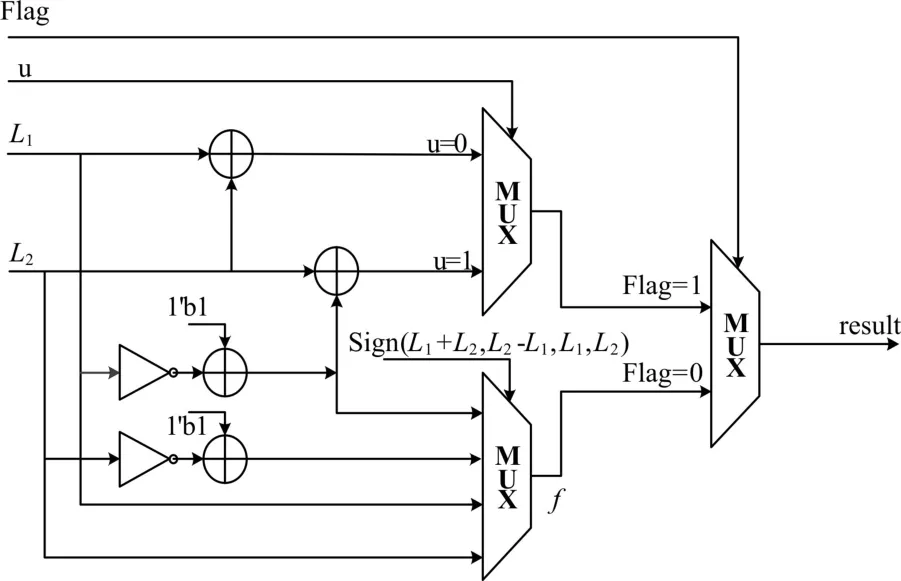
图6 计算单元PE硬件结构

其中，f节点的输出选择信号sign为sgn(L2+L1)⊕sgn(L2-L1)、sgn(L1)和sgn(L2)三者的拼接，其8种状态所对应的输出如下：1）000：L1；2）001：L1；3）010：L1；4）011：L1；5）100：L1；6）101：L1；7）110：L1；8）111：L1。

由于g节点的计算由加（减）法构成，因此在计算的过程中就存在溢出的可能性，如果不加以处理，随着计算层数的增加，LLR的位宽会变得越来越大。对此，我们对g节点输出的结果均除以2。

4.3 修正模块

在进行这样的处理之后，g节点的计算结果与预期结果不同，会导致最后得到的顶层LLR与预期值相差2n倍，n为在一次计算顶层LLR过程中所经过路径含有g节点的数量，即IDX信号中1个个数。因此，在顶层LLR计算完成后与进行度量值计算前需要添加一个修正模块还原正确的LLR值。所以，该模块的功能为根据IDX信号中1的个数n对LLR做乘2n处理。如果最终得到的LLR新值已经超过了度量值的位宽，则输出溢出信号给后面的度量值计算模块。

4.4 度量值计算模块

如图7所示为路径度量值计算模块的硬件结构图。

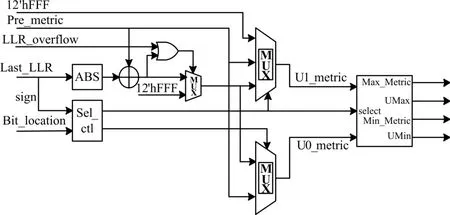
图7 度量值计算模块硬件结构

在经过修正模块的修正得到32条路径对应的顶层LLR之后，要对当前2L=64条路径的度量值进行计算。我们用一块1024*1的ROM存放信息比特和冻结比特的位置信息，0对应冻结比特，1对应信息比特，如图4中Bit_location ROM所示。当本模块开始工作时，从Bit_location ROM中读取位置信息Bit_location，和顶层LLR的符号位一起作为Sel_ctl控制模块的输入，来控制公式中所对应的三种情况。

在计算出候选比特为0和1格子的路径度量值后，使用一个选择器输出其中的较大值和较小值以及他们对应的候选比特。所以在2L条路径送入排序模块之前，我们可以对齐进行初步排序，根据顶层LLR的符号位，将路径i分支出来的两个度量值中较大的放在第i个位置，较小的放在第i+L个位置。这样做是因为当前错误比特对度量值的影响往往比不同路径对度量值带来的影响要大，当将数据送入排序模块进行排序后可以显著减小排序算法的收敛时间。

4.5 排序模块

对路径度量值计算模块传送过来的条路径进行冒泡排序，将前32个输出路径度量值结果存于Metric_reg寄存器中，用于下次路径度量值的计算。同时输出结果格式为：最高位代表所选择的比特，后五位代表所属的上一层的路径，这样有利于路径恢复模块从排序结果恢复出路径，将此结果输出至反馈模块。

4.6 反馈模块

在经过排序模块之后得到了32条候选路径所对应的顶层估计比特和相应的路径索引，反馈模块的作用就是据此更新下一次计算所需要的g节点u^s的值，并把结果存入RAM（图4中Feedback RAM），最终反馈至LLR计算模块输入端。反馈模块的结构与LLR的计算结构相似，数据的流动方向是相反的，仍以N=8为例，如图8所示。

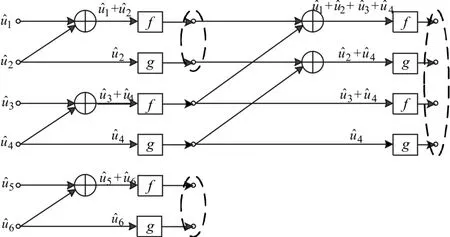
图8 N=8时反馈模块结构

计算规则如下：1）新生成的比特先存入顶层，如图中最左侧所示；2）判断当前层的IDX值，如果为0则将当前层的数据存入下一层的 f单元。如果是1，则将当前层的数据存入下一层的g单元，并取出 f中的数据与当前层数据相加后继续存入f单元，然后以规则2）继续下一层的计算。这里的f和g单元只有存储功能，并没有LLR计算模块中f和g单元的计算功能。令LLR计算模块中数据的读地址和u^s的读地址相同，保证了当前计算g节点的正确性。

4.7 路径恢复模块

本模块的功能为从排序结果中将路径提取出来，这样使得在SCL译码模块中不再需要对路径进行保存和复制。初始状态下，将32条空路径设置索引号0～31，每条路径按照自己的索引从最后一个比特的位置读取排序结果，提取相应的码字。然后根据排序结果来更新下一次要读的索引，重复此步骤直到读到第一位比特，最终将输出的码字发送到Result_RAM中，其深度为512，数据位宽为32。

4.8 控制模块

由控制模块生成的IDX信号实质上控制这整个译码器的工作状态，当IDX=1111111111，下一状态为全0表示译码器已完成全部比特的译码。在状态机的控制下，控制模块通过严格的时序保证各个模块之间协同有序的工作。

4.9 CRC串行译码模块

由于恢复模块的原因，译出来的信息比特以逆序排列，逆序的CRC校验码在逆序信息比特序列前面，且序列为串行输出。故CRC译码模块采用了串行逆序译码结构，与并行译码相比减少了资源消耗而且所需时间并不会发生改变。该模块如图9所示使用了24个寄存器用于存放CRC检验码。译码开始，前24个时钟输入的是CRC校验码，按顺序存入24个寄存器中，从第25个数据开始按下图的数据流向计算，根据生成多项式生成加法器。整个结构如图9所示。

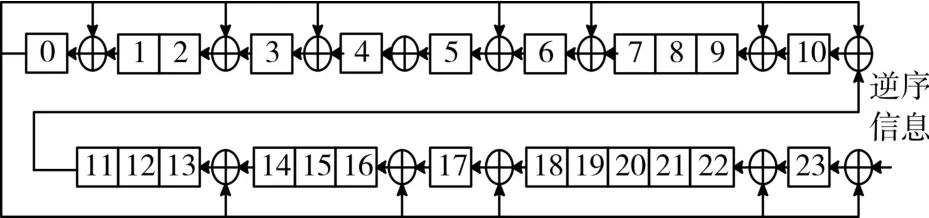
图9 CRC串行逆序译码模块

5 仿真结果与分析

在本文的极化码SCL译码器设计实现的过程中，采用的FPGA芯片是Altera公司Strtix V系列的5SGXEA7H3F35C3，使用 QuartusⅡ15.0综合后的结果如表1所示。

表1 极化码CA-SCL译码器硬件资源统计

本文设计中，码长为1024，译码器的工作频率为300MHz。译码器平均时延为0.164ms，所以吞吐率可以达到1024/(0.164×10-3)=6.24Mbps。可以观察到，本文设计的译码算法译出一个码字大概需要49000个时钟周期，而系统面积的占用率仅为6%。

如图10所示，为对数据进行8位定点量化、对路径度量值进行12位定点量化后的CA-SCL算法性能与浮点计算（未量化）的性能之间的比较。由于浮点数无法被EDA工具所综合，在实现中必然要使用量化后的数据，并将其转化为二进制比特。在转换的过程中损失了一定的计算精度，性能自然要比浮点计算差。在误码率BER=10-3时，二者性能相差大约0.1dB，故译码器的硬件实现也可以获得接近于浮点计算的性能。

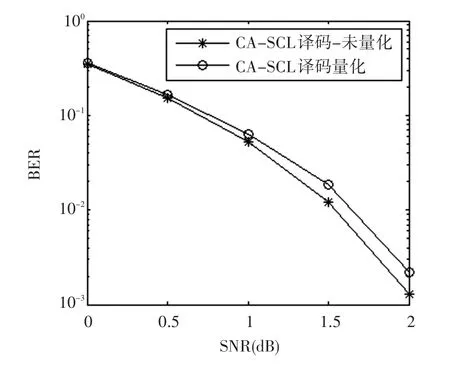
图10 量化与未量化CA-SCL译码算法比较

6 结语

对码长为1024的极化码采用了公认性能优良的CA-SCL译码算法，对每条候选路径运用计算单元的硬件架构，完成了对该算法占用较大系统面积的优化，在此情形下的吞吐率表现并没有达到理想状况。为了进一步在速度与面积之间取得平衡，后续将对大量调用的单计算单元结构进行优化以减小关键路径的长度，从而提高系统频率降低平均时延。

［1］Arikan E.Channel Polarization：A Method for Construct⁃ing Capacity-Achieving Codes for Symmetric Binary-In⁃put Memoryless Channels［J］.IEEE Transactions on Infor⁃mation Theory，2009，55（7）：3051-3073.

［2］Shannon C E.A Mathematical Theory of Communication［J］.Bell Labs Technical Journal，1948，5（4）：3-55.

［3］Tal I，Vardy A.List decoding of polar codes［C］//IEEE In⁃ternational Symposium on Information Theory Proceed⁃ings.IEEE，2011：1-5.

［4］Niu K，Chen K.CRC-Aided Decoding of Polar Codes［J］.IEEE Communications Letters，2012，16（10）：1668-1671.

［5］Niu K，Chen K，Lin J，et al.Polar codes：Primary con⁃cepts and practical decoding algorithms［J］.IEEE Commu⁃nications Magazine，2014，52（7）：192-203.

［6］Leroux C，Tal I，Vardy A，et al.Hardware architectures for successive cancellation decoding of polar codes［J］.2010，125（3）：1665-1668.

［7］Leroux C，Raymond A J，Sarkis G，et al.Hardware Imple⁃mentation of Successive Cancellation Decoders for Polar Codes［J］.Journal of Signal Processing Systems，2012，69（3）：305-315.

［8］Leroux C，Raymond A J，Sarkis G，et al.A Semi-Parallel Successive-Cancellation Decoder for Polar Codes［J］.IEEE Transactions on Signal Processing，2013，61（2）：289-299.

［9］Zhang C，Yuan B，Parhi K K.Reduced-latency SC polar decoderarchitectures［J］.ComputerScience，2011：3471-3475.

［10］Zhang C，Parhi K K.Low-Latency Sequential and Over⁃lapped Architectures for Successive Cancellation Polar Decoder［J］.IEEE Transactions on Signal Processing，2013，61（10）：2429-2441.

［11］Lin J，Xiong C，Yan Z.A High Throughput List Decoder Architecture for Polar Codes［J］.IEEE Transactions on Very Large Scale Integration Systems，2015，24（6）：2378-2391.

［12］Balatsoukas-Stimming A，Raymond A J，Gross W J，et al.Hardware Architecture for List Successive Cancella⁃tion Decoding of Polar Codes［J］.Circuits&Systems II Express Briefs IEEE Transactions on，2014，61（8）：609-613.

［13］Balatsoukas-Stimming A，Bastani Parizi M，Burg A.LLR-Based Successive Cancellation List Decoding of Po⁃lar Codes［J］.IEEE Transactions on Signal Processing，2015，63（19）：5165-5179.

［14］Arikan E.Systematic Polar Coding［J］.IEEE Communi⁃cations Letters，2011，15（8）：860-862.

［15］Arikan E.Channel combining and splitting for cutoff rate improvement［J］.IEEE Transactions on Information The⁃ory，2005，52（2）：628-639.

［18］Li H，Yuan J.A practical construction method for polar codes in AWGN channels［C］//Tencon Spring Confer⁃ence.IEEE，2013：223-226.

［19］Mori R，Tanaka T.Performance of polar codes with the construction using density evolution［J］.IEEE Communi⁃cations Letters，2009，13（7）：519-521.

［20］Tal I，Vardy A.How to Construct Polar Codes［J］.IEEE Transactions on Information Theory，2013，59（10）：6562-6582.

［21］Peterson W W，Brown D T.Cyclic Codes for Error Detec⁃tion［J］.Proceedings of the Ire，1961，49（1）：228-235.

［22］Fossorier M P C，Mihaljevic M，Imai H.Reduced com⁃plexity iterative decoding of low-density parity check codes based on belief propagation［J］.IEEE Transactions on Communications，1999，47（5）：673-680.