末制导雷达动态精度试验数据处理方法研究∗

张安民 王 宁

（91336部队 秦皇岛 066000）

1 引言

跟踪精度是评价末制导雷达重要的战术技术指标之一，直接影响其侦察、定位能力。动态精度试验一直是靶场在对末制导雷达进行定型、鉴定试验时的重点试验内容。通过对以往试验数据进行分析可以看出，在典型航路上末制导雷达动态误差可以看作是一个正态随机过程，通过多个航次的试验得到的精度误差是多个离散化的值，利用传统数理统计方法可以得到每个记录时刻的误差值。但是，跟踪精度的指标是全航路平均的精度指标，如何获得全航路的平均是本文重点研究的内容。

末制导雷达跟踪误差数据从长时间全过程来看是非平稳的，而从各局部较短时间来看是平稳的，即信号的统计特性在一些时刻发生突变，而在这些时刻之间能够保持平稳性。在统计学上，这类信号被称为分段平稳的随机信号。在平稳段内各时刻的跟踪误差具有相同的分布，从统计学的角度可以把它们看作同一个正态总体，对跟踪误差的统计值先在每个平稳段内进行，然后通过加权平均得到全航路的估计值［1］。

本文在深入分析研究分段平稳随机信号的基础上，设计了基于分段平稳随机信号的末制导雷达跟踪精度试验数据处理策略，以某型末制导雷达方位跟踪精度试验数据为例，按照该策略的方法和步骤进行了数据处理，可为其它类似数据处理提供方法借鉴和参考。

2 分段平稳随机信号

在统计学内，将某阶统计量随时间改变的随机信号称为非平稳随机信号，其统计特征是时间的函数。目前，非平稳随机信号还没有统一的描述方法。有一种非平稳随机信号，其统计特性在某些未知的时刻突然变化，而在这些时刻之间保持平稳性，这些突变时刻称为分界点，在分界点间的各平稳段可以用平稳随机信号的参数模型来表示。这类非平稳随机信号称为分段平稳随机信号，末制导雷达跟踪精度试验数据即为该类型的非平稳随机信号。

处理分段平稳随机信号的关键在于如何分段。

2.1 简单分段平稳随机信号

设简单的分段平稳随机信号为如下二分段情况：

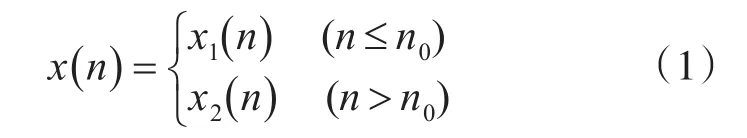
式中：x1(n)与x2(n)都是平稳的随机序列，其统计特性不同。

对这种简单的二分段平稳随机信号，可以应用信息论判阶准则（AIC）来判断如何分段。

2.2 一般分段平稳随机信号

对于大多数分段平稳随机信号来说，二分段是最简单的处理方法，大多数情况为一般N段的情况，即 x(n)=xi(n)(ni＜n＜ni+1;i=0，1，…，N-1) ，其中xi(n)均为不同的平稳随机信号，在平稳随即信号参数模型中，最常用的是AR模型，故可通过对每个区间规定不同的AR模型来描述x(n)的特性［2］。

分析一般分段平稳随机信号，需要解决以下三个问题：

1）分段的段数；

2）各段之间分界点的确定；

3）各段AR模型的选择。

P.M.Djuric等在参考文献［3］中采用贝叶斯定理对上述问题进行了研究，导出了一个关于分段数、各段AR模型阶数及各段之间分界点的优化方程。这种方法不需要设置任何门限，适用范围广泛，但由于优化方程求解非常复杂，计算量很大，限制了它的实际应用。参考文献［4］对此优化方程作了进一步研究，得出了可使计算能够见效的简化解法，并对如何使用搜索法求解优化方程做了阐明。

按照最大验后估计最优准则，参考文献［3］给出的求解分段数、各段AR模型阶数及各段之间分界点估值（q^，p^q，j^q-1）的分段平稳化方程为

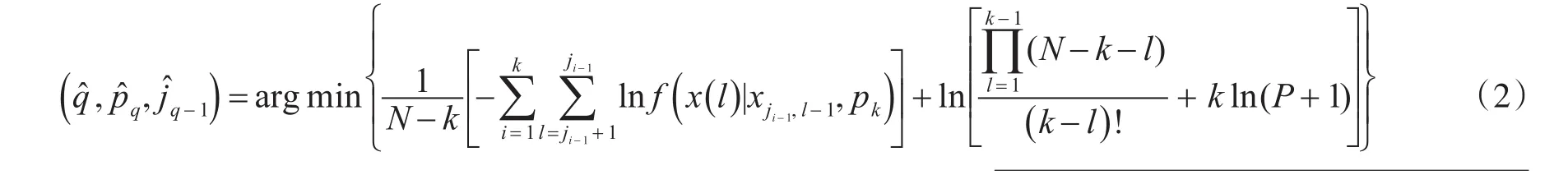
式中，k∈(1，2，…，Q)；arg表示自变量。

分段平稳优化方程式（2）虽可用动态规划法求解，但是非常繁难。目前普遍采用搜索法［4］进行求解，步骤如下：

1）先令q=1，即将整个数据序列作为1段，改变AR模型阶数，计算不同阶数情况下式（2）及AIC值，取使AIC值最小的阶数作为模型阶数，记下与此模型阶数对应的式（2）的值，以便最后比较。

2）其次q=2，将整个数据序列作为2段，这时需改变前、后2段AR模型的阶数 p1、p2及分界点j的 位 置 。 让 ：j1=j0+2，j0+3，…，N-2(j0=1)；p1=0，1，…，P ；p2=0，1，…，P 。逐点搜索，按照与步骤1类似的方法，取值、比较，得出式（2）最小。

3）依此类推，令q=3，4，…，Q，按照上述方法进行计算、取值、比较，记下式（2）最小值。

4）完成上述全部搜索后，其中与式（2）最小值所对应的分段数、模型阶数、分界点即为所求。

3 数据处理策略

3.1 处理策略与步骤

根据上述分段平稳随机过程的分析可知，将试验数据按照一定的原则进行分段处理，可将分段后的数据按照平稳随机信号的处理方法进行分析。

基于分段平稳随机信号的测向试验数据处理的策略和步骤设计如下［5］：

1）数据预处理，即异常值的判断与处理；

2）数据分段，即应用2.2节介绍的方法将数据进行分段处理；

3）误差统计特性计算，即对分段后的数据计算标准差；

4）指标的假设检验，即应用试验数据（样本数据）对末制导雷达跟踪精度进行统计推断。

3.2 数据预处理

数据预处理是进行试验数据处理的前提和基础，主要用于找出测量过程中产生的误差（即异常值）。预处理的过程就是对所得数据的异常值进行识别的过程，并将异常值剔除或补正。剔除异常值后，还需要采用线性插值法，根据采样周期补充相应的数据。

用统计方法判别异常值的基本思想是［6］：给定一个检验水平，并确定一个置信限，凡误差超过这个置信限的测量值，被认为不属于正常值范畴，而当作异常值剔除。判别测量异常值的方法很多，在电子装备试验中常用以下两种方法：Layite方法和Grubbs方法。本文拟采用Layite方法对末制导雷达跟踪精度的试验数据进行预处理，下面对Layite方法作简要介绍［7］。

Layite方法按正态分布理论，以最大误差范围3s为依据进行判别，设有一组测量值xi(1，2，…，n) ，其 样 本 平 均 值 为 xˉ，偏 差Δxi=xi-xˉ，按式（3）计算标准差 s：

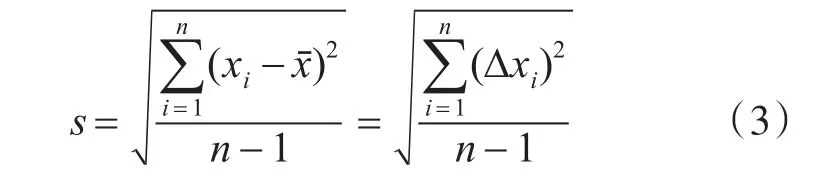
如果某测量值 xl(1≤l≤n)的偏差 ||Δxl＞3s时，则认为xl是异常值。

该方法最大的优点是简单、方便、不需查表，但对小样本数据不准确，往往会把一些异常值隐藏下来而犯“存伪”的错误。

3.3 假设检验

在电子对抗装备试验中，被试品标准差指标的形式通常为σ≤σ0，σ0是已知常数。在对总体情况利用假设检验的方法进行推断时［8］，主要对下面两种情况之一进行检验：

1）检验被试品满足“σ≤σ0”；

2）检验被试品不满足“σ≤σ0”。

末制导雷达跟踪精度试验主要是针对第一种情况进行检验，下面对该检验方法作简要介绍。

要检验的假设是［9］：

由于样本方差S2是总体方差σ2的无偏估计，对于该检验问题常用的检验方法是：S2≤c时拒绝H0，S2＞c时接受H0。常数c是根据事先选定的检验水平α确定的，且当H0∶σ＞σ0时成立时满足

当 X～N（μ，σ2）时，(n-1)S2σ2～，以 K表示的分布函数，那么

于是根据实际推荐原理可得改检验问题的如下判别准则：

4 实例分析

4.1 末制导雷达方位跟踪精度试验设计

末制导雷达方位跟踪精度试验典型态势如图1所示［10］。

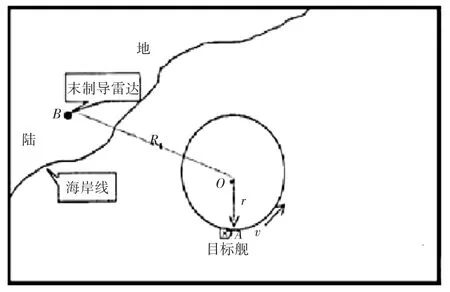
图1 末制导雷达方位跟踪精度试验典型态势图

目标舰A点就位，末制导雷达架设在B点，两者距离为R，末制导雷达开机稳定跟踪目标并记录相关数据；目标舰以O点为圆心，r为半径，以航速v作匀速圆周运动。

4.2 数据处理过程

按照上述试验过程得到试验数据，同时通过GPS定位系统得到目标舰的方位真值数据，将两者相减得到每一个测量时刻的方位误差，将数据平方后如图2所示。

图2 试验数据

针对上述试验数据，按照3.1所介绍的流程对数据进行处理，所用到的方法均通过编写Matlab程序实现。

4.2.1 数据预处理

首先运用Layite方法对数据进行预处理，找出异常值并剔出，将剔除值用其左右数据的均值代替，预处理后的数据如图3所示。

图3 预处理后试验数据

4.2.2 数据分段

利用式（2）对预处理后地数据进行分段，将非平稳随机信号化为多段平稳随机信号。

分别令q=1、2、3…100，按照2.2介绍的方法计算AIC的值，计算结果见下表。

表1 数据AIC计算值

从表1可以看出，当阶数取47时，AIC的值最小，可将数据分为47段平稳随机信号，并根据式（2）求出分界点。

4.2.3 统计特性计算及统计推断

分别计算各段数据的标准差，计算结果见表2。

数据的标准差为0.5253。取σ0=0.95，利用假设检验的方法进行统计推断。计算得，拒绝H0，可判定被试品标准差满足指标要求。

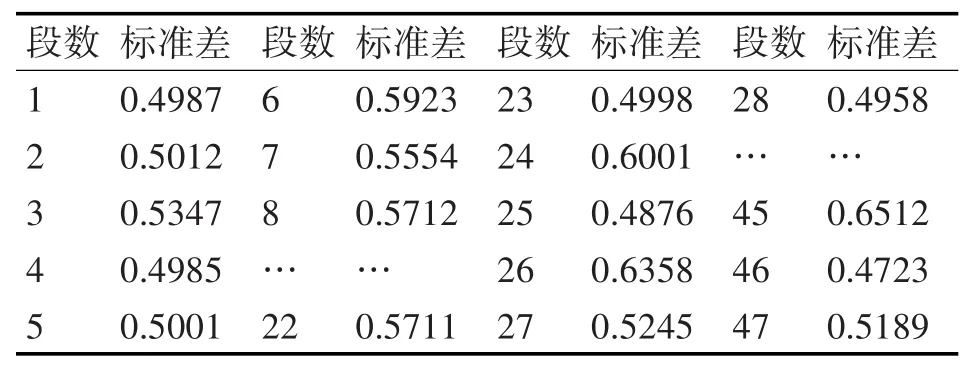
表2 各数据段标准差

5 结语

本文提出了一种基于分段平稳随机过程的末制导雷达动态跟踪精度试验数据处理方法，利用该方法克服了试验数据处于非平稳随机状态下无法利用传统统计学方法进行分析的问题，并最大限度保留了原始数据的信息。首先设计了基于分段平稳随机信号的测向误差试验数据处理策略，以某型末制导雷达方位跟踪精度试验数据为例，按照该策略的方法和步骤进行了数据处理，从处理结果来看，分段平稳随机过程在非平稳随机信号的数据处理中可以发挥重要作用。

［1］王宏禹，邱天爽，陈喆.非平稳随机信号分析与处理［M］.北京：国防工业出版社，2008，04：101-125.

WANG Hongyu，QIU Tianshuang，CHEN Zhe.Nonstation⁃ary Random Signal Analysis and Processing［M］.Beijing：National Defense Industry Press，2008，04：101-125.

［2］包国忱，柴义隆.电子装备试验数据处理［M］.北京：国防工业出版社，2002，01：315-332.

BAO Guochen，CHAI Yilong.Electronic Equipment Test Data Processing［M］.Beijing：National Defense Industry Press，2002，01：315-332.

［3］Djuric P M，Kay S M，Faye B G.Segmentation of nonsta⁃tionary signals［J］.Proc.IEEE ICASSP，San Francisco，1992：161-164.

［4］王文华，王宏禹.分段平稳随机过程的参数估计方法［J］.电子科学学刊，1997，19（3）：311-317.

WANG Wenhua，WANG Hongyu.A Research on segmen⁃tation of nonstationary stochastic process into piecewise stationary stochastic process［J］.Journal of Electronics，1997，19（3）：311-317.

［5］ORFANIDIS S J.Introducetion To signal Processing［M］.Prentice Hall International，Inc.1999：84-88.

［6］张贤达，保铮.非平稳信号分析与处理［M］.北京：国防工业出版社，1990：105-122.

ZHANG Xianda，BAO Zheng.Nonstationary Signal Analy⁃sis and Processing［M］.Beijing：National Defense Industry Press，1990：105-122.

［7］Chen Z，Wang H Y，Qiu T S.A TVAR parametric model based on WNN［J］.ICNNSP，Nanjing，2003：802-805.

［8］张海勇.基于局域波法的非平稳随机信号分析中若干问题的研究［D］.大连：大连理工大学，2001：32-35.

ZHANG Haiyong.research on some problems of non-sta⁃tionary random signal analysis based on local wave method［D］.Dalian：Dalian University of Technology，2001：32-35.

［9］曹渊.导弹末端导引精度小子样试验评估方法研究［D］.长沙：国防科学技术大学，2008：15-23.

CAO Yuan.Research on missile terminal guidance accura⁃cy of small sample test evaluation method［D］.Changsha：National University of Defense Technology，2008：15-23.

［10］邱轶兵.试验设计与数据处理［M］.北京：中国科学技术大学出版社，2015：44-47.

QIU Yibing.Experiment Design and Data Processing［M］.Beijing：University of Science and Technology of China Press，2015：44-47.