随机化快速选择算法时间复杂度研究∗

刘显德 于瑞芳 李盼池 刘晓明

（东北石油大学计算机与信息技术学院 大庆 163318）

1 引言

算法是计算机科学的灵魂，某些经典的算法往往只有很少几行，但是却能解决很多大问题。随机算法可以分为三大类，即Las Vegas型算法、Monte Carlo型算法和Sherwood型算法［1］。Las Vegas型算法建立的那些随机算法总是或者给出正确的解，或者算法求解失败，但是再次运行算法就有成功的可能［2］。而Monte Carlo型算法总是给出解，但是偶尔可能会产生非正确的解。Sherwood型算法的思想方法在于在原有的确定型算法基础上，引入随机化因素，改变问题的输入或求解顺序，设法消除算法的时间复杂度与输入实例之间的关系［3］。文献［4］提出了用Java来设计算法的一种方法，文献［5］提出了一种改进的随机算法，可以使得算法执行比较的期望次数减少到小于3n，文献［6］提出Las Vegas算法可以看成是Monte Carlo算法当错误概率为零时的情况，文献［7］提出应用分段线性分布模型来模拟随机算法运行时间分布的一种方法，文献［8～10］研究了随机算法异步并行化问题。本文研究的随机化快速选择算法即属于Sherwood型算法。

2 算法复杂度分析

2.1 最坏时间复杂度

在最坏情况下，随机数发生器在 j次循环时选择第 j个元素，j=1，2，…，n，这样只有一个元素被抛弃，由于把A分成A1，A2和A3所需要的比较次数恰好为n，所以算法在最坏情况下所做的元素比较的总次数是

设随机数发生器在某个闭区间产生的随机数满足均匀分布，则发生这种最坏情况概率为

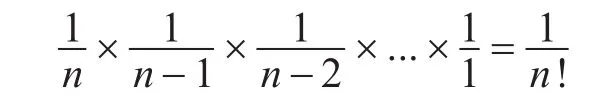
另一种最坏情况是随机数发生器在 j次循环时选择第 n-j+1个元素，j=1，2，…，n，这种最坏情况仅仅是理论上存在，实际中几乎不可能发生。

2.2 最好时间复杂度

算法的最好时间复杂度为C(n)=n，若随机数发生器第1次随机选择的元素恰好是待查找的第k小元素，则经过算法的第3步共n次元素比较，将元素分为三个部分，再经过第4步的判断，即查找成功。因此最好时间复杂度为C(n)=n，发生这种最好情况的概率为1/n。

2.3 期望时间复杂度

在本文中，运用概率论分析方法，通过理论分析和实验研究两种途径，从更小的信息粒度意义上深入研究这个随机算法，给出其期望复杂度的三种情况，即最好情况、最坏情况和平均情况，分别得到最好情况的紧下界、最坏情况的一个比较紧致的上界，更重要的是，得到了平均情况的一个数学紧上界，作为本文一个重要理论研究成果。

进行如下理论分析：

设有数组 A[i…j]，取定 k∈[i，j]作为分割点，记Xj-i+1表示经过这一次分割所得到的余下的数组长度（条件）期望值。则分割后，余下的数组为如下序列之一：A[i…k-1]，A[k]，A[k+1…j]。设分割点k∈[i，j]满足均匀分布，则落在以上3个区间内的概率与区间长度成正比，即分别为：（k-i）/（j-i+1），1/（j-i+1），（j-k）/（j-i+1）。

则将 A[i…j]一次分割后，余下数组长度（条件）期望值是

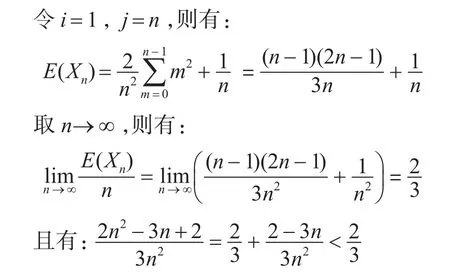
这说明在计算期望时间复杂度时，一次递归可以去掉至少1/3的元素，剩余元素的个数期望值不超过上次元素个数的2/3。于是，可得：

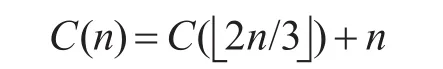
其中 +n表示经过n次比较。易知当n=1时，C(1)=1。

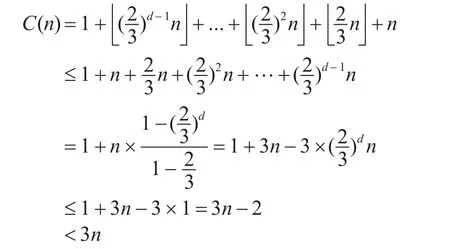
由以上的证明可知：随机化的快速选择算法的期望时间复杂度小于3n。

3 研究目标和实验设计

3.1 研究平台

本文使用C++语言作为编程语言，采用Matlab进行数据处理编程。

3.2 研究目标

由于随机化选择算法中采用了随机算法，对于同一个k，当随机算法生成的基准元素不同时，所得到的结果相差很大，因此在计算相应时间复杂度时，这是首先要解决的一个问题。考虑k变化时的情况，从更小信息粒度意义上深入研究这个随机算法，给出其期望复杂度的最好情况、最坏情况和平均情况，进而期望找到算法时间复杂度的一个比较紧致的上界，最好是其紧上界，作为对该算法复杂度的一个最佳描述。

3.3 实验设计

1）随机生成n个数（先取n=100），for k=1 to n，执行算法，记录每次的比较次数C（n，k），分析C（n，k）变化趋势；

2）重复步骤1），对比观察得到的实验数据，分析其中规律；

3）生成n（先取n=100）个元素的数组A［i］，其中A［i］=i，构成升序数组，for k=1 to n，记录每次的比较次数C（n，k），分析C（n，k）的变化趋势；

4）分别取 n=512，1024，2048，4096，然后重复步骤3），观察一系列图，发现其中变化规律；

5）重复步骤3）和步骤4），但是其中的A［i］=n-i+1，构成降序数组，其它不变，观察其变化规律；

6）分别取n=512，1024，2048，4096，对于每个n分别采用3组随机生成的数组，一组升序数组A［i］=i，一组降序数组A［i］=n-i+1作为输入数组，for k=1 to n，记录每次的比较次数；

7）分别取 n=128，256，512，1024，2048，4096，8192，随机生成n个数，for k=1 to n，记录每个n值下的最大时间复杂度和时间复杂度的中位数；

8）重复有限次实验7，获得每个n值下的多组最大时间复杂度和时间复杂度的中位数。对于每个n，保留其中最大时间复杂度中的最大值以及时间复杂度的中位数；

9）取n=1000，随机生成n个数，分别取子序列长度为5，7，9，13，17，for k=1 to n记录每次的比较次数C（n，k），保留其中每个子序列长度下最大的C（n，k）；

10） 分 别 取 n=5000，10000，20000，50000，100000，200000，重复步骤9）；

11）取n=100，随机生成n个数，for k=1 to n，每次确定n和k值以后，分别运行程序1，10，100，记录每组运行的统计平均值与随机实验次数之间的变化规律；

12）在步骤11）的数据分析基础上，取n=2，3 to 100，每次随机生成n个数，for k=1 to n，对于每个k运行程序次，记录每次比较次数的统计平均值 ，观察记录 关于参数k的最小、最大与平均值情况，作为当前输入规模为n时的最好、最坏与平均时间复杂度的度量。

4 实验结果分析

4.1 时间复杂度的研究

随机化的选择算法中因为随机算法的存在，导致该算法每次执行所得到的比较次数相差较大。因此取m次重复实验结果的平均值作为其时间复杂度。为了验证这个m值取多大合适，我们进行了如下实验：取数组n的大小为100，即n=100，然后对于每个k，分别进行1，10，100，1000，10000次的重复随机实验，得到其每次实验的时间复杂度C(n，k)，然后分别取其平均值 。以为纵坐标，k为横坐标得到图1。

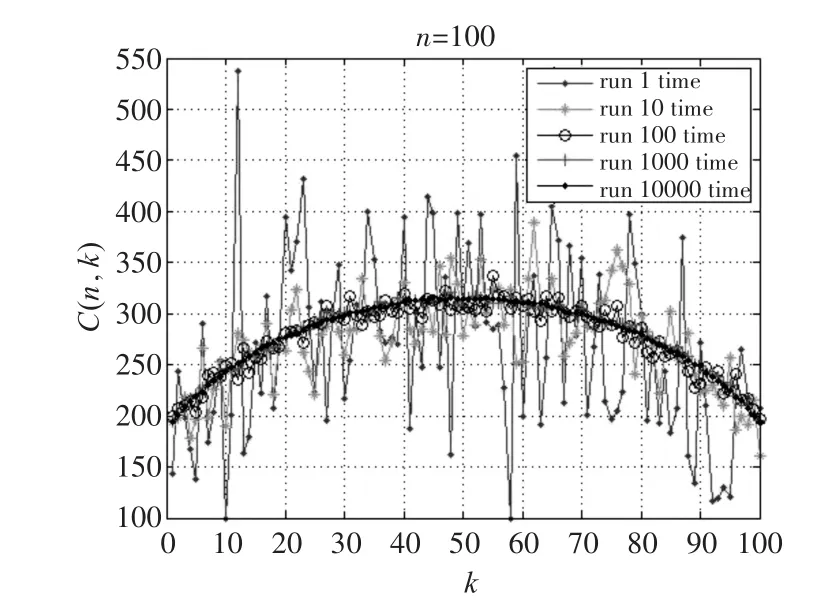
图1 随机实验次数与相应结果的变化图

正如图1中所看到的，当随机实验重复次数为1次时，所得到的曲线是杂乱无章的，如波浪般。当随机实验重复次数为10次时，所得曲线仍是上下起伏的，但是起伏程度明显低于随机实验重复次数为1次时的曲线。当随机实验次数为100次时，所得曲线已经趋向于平缓，但是也有一些涨落。当随机实验次数为1000次，10000次时，实验所得曲线已经非常的平滑，两者基本相同。换言之，平均值逐渐收敛。

4.2 时间复杂度的平均值

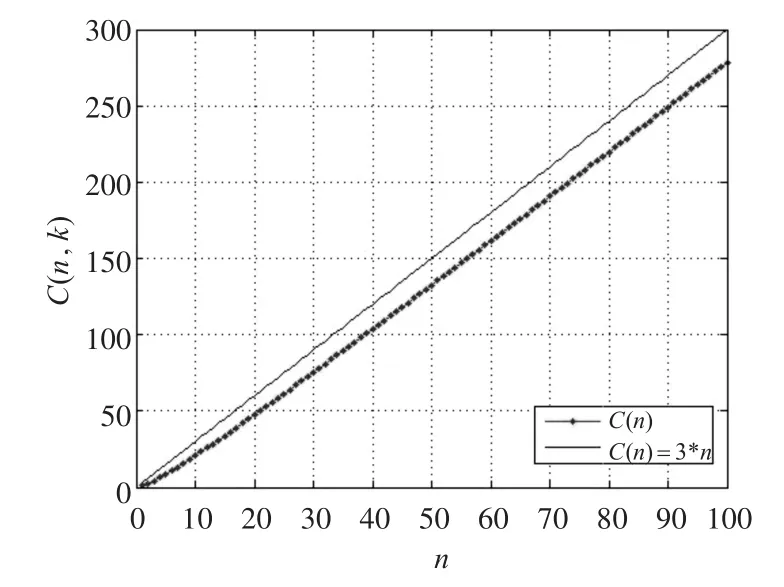
图2 时间复杂度平均值曲线图

从图2中可以看出，时间复杂度平均值的图象在n较小时有一定的弯曲，但是随着n的增大，图象就开始呈现为线性变化，而且一直在C(n)=3n的下方，实验数据完全符合我们的理论模型。换言之，我们通过理论推导并进行实验数据验证的方式，得到了该算法期望时间复杂度函数的紧上界3n。

4.3 时间复杂度的最大值

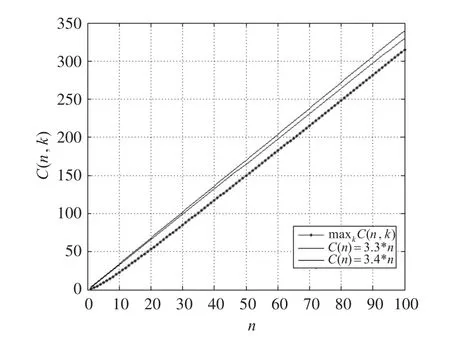
图3 时间复杂度最大值曲线图

从图3中可以看出时间复杂度最大值的拟合曲线在C(n)=3.3n的下方，但是，随着n的增大，其最大值曲线是否会发生变化。为了研究其具体情况，我们又进行了更多的实验，将问题规模n扩大，再重复上面的实验，然后绘制相应的最大值曲线图，得到图4。

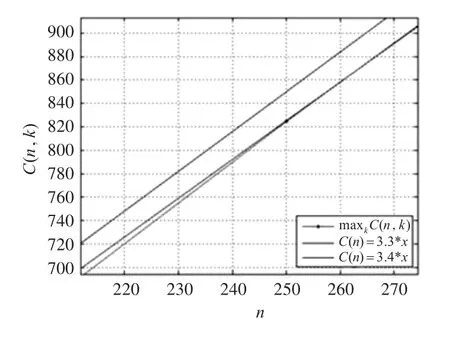
图4 时间复杂度最大值的补充曲线图

从图4中可以看到，当n在250～350之间的某个值时，最大值的拟合曲线超过了C(n)=3.3n，而一直在C(n)=3.4n的下方，并且非常靠近C(n)=3.4n。为了研究该最大值是否还会有变化，我们又将n值进行扩大，做了一些针对性的实验，但是该最大值的拟合曲线没有更多变化，即期望时间复杂度的上界（最大值）小于3.4n，至于理论上的分析，还有待于进一步的研究。

4.4 时间复杂度的最小值

图5 时间复杂度最小值曲线图

从图5中观察可知，时间复杂度最小值的拟合曲线图一直位于C(n)=n的上方，但是和C(n)=1.1*n在n很小时会有交点。因为当n=1时，C（1）=1，又因为每个元素至少被检查一次，C(n)≥n，所以随机化的选择算法所期望的元素比较次数的下界为n。

5 结语

经过上面的实践研究，我们对随机化的快速选择算法有了更好的认识。通过实践获得相应的实验数据，对大量实验数据进行汇总处理，然后将其绘制成曲线，通过分析实验数据和观察相应的曲线，发现了一些规律。由于该算法中存在随机函数，因此其不确定性相对较大，即实验结果会有较大波动，但是通过大量的随机实验，发现多次随机实验平均值会随着实验次数的增多而逐渐收敛，从而降低实验误差，为实验成功进行提供了基础保证。当n处于一定的范围内，计算得到了该算法时间复杂度数据，并在此基础上，分析了其平均值、最大值以及最小值。综上得到如下结论：ffffbc

［1］邹亮，徐建闽，朱玲湘.A～*算法改进及其在动态最短路径问题中的应用［J］.深圳大学学报，2007，24（1）：32-36.

ZOU Liang，XU Jianmin，ZHU Xiangling.Improvement of A*Algorithm and its Application in Shortest Path Problem in Dynamic Networks［J］.Journal of Shenzhen University Science and Engineering，2007，24（1）：32-36.

［2］段莉琼，朱建军，王庆社.改进的最短路径搜索A*算法的高效实现［J］.海洋测绘，2004，24（5）：20-22.

DUAN Liqiong，ZHU Jianjun，WANG Qingshe.Fast Real⁃ization of the Improved A*Algorithm for Shortest Route［J］.Hydrographic Surveying and Charting，2004，24（5）：20-22.

［3］樊莉，孙继银，王勇.人工智能中A～*算法的应用及编程［J］.微机发展，2003，13（5）：33-35.

FAN Li，SUN Jiyin，WANG Yong.Application and Pro⁃gramming of A*Algorithm in AI［J］.Microcomputer De⁃velopment，2003，13（5）：33-35.

［4］夏永锋，曹元大.启发式搜索算法的面向对象设计实现［J］.微机发展，2005，15（7）：11-13.

XIA Yongfeng，CAO Yuanda.Implementation and Design Heuristic Searching Algorithm by Object-Oriented Method［J］.Microcomputer Development，2005，15（7）：11-13.

［5］周鹏.一种改进的随机选择算法［J］.三峡大学学报（自然科学版），2007，29（5）：470-473.

ZHOU Peng.An Improved Randomized Selection Algo⁃rithm［J］.Journal of China Three Gorges University（Natu⁃ral Sciences），2007，29（5）：470-473.

［6］贺红，马绍汉.随机算法的一般性原理［J］.计算机科学，2002，29（1）：90-92.

HE Hong，MA Shaohan.The General Principles of Ran⁃domized Algorithms［J］.Computer Science，2002，29（1）：90-92.

［7］徐云，陈国良，张强峰，等.随机算法异步并行化的效率分析［J］.软件学报，2003，14（5）：871-876.

XU Yun，CHEN Guoliang，ZHANG Qiangfeng，et al.Effi⁃ciency Analysis of Asynchronic Parallelization of Random⁃ized Algorithms［J］.Journal of Software，2003，14（5）：871-876.

［8］Gu J，Purdom PW，Franco J，Wah BW.Algorithms for satisfiability（SAT） problem：A survey［J］.DIMACS Se⁃ries in Discrete Mathematics and Theoretical Computer Science，American Mathematical Society，1997（35）：19-151.

［9］Gomes C，Selman B，Kautz H.Boosting combinatorial search through randomization［M］.Proceedings of the AAAI-98.Madison：AAAI Press，1998：430-437.

［10］Gomes C，Selman B，Crato N，Kautz H.Heavy-Tailed phenomena in satisfiability and constraint satisfaction problems［J］.Journal of Automated Reasoning，2000（24）：67-71.