基于直觉模糊MULTIMOORA的改进FMEA风险评估方法

王 睿，朱江洪，李延来,2+

(1.西南交通大学 交通运输与物流学院，四川 成都 610031； 2.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 610031)

0 引言

故障模式和影响分析(Failure Mode and Effects Analysis, FMEA)方法最早于上世纪60年代提出，用于航空航天业中设备可靠性检测和风险评估研究[1]。此后，经过多年理论探索和实际运用效果分析，FMEA方法已广泛应用于航空航天业、电力电子业、核工业和手工业等企业，以确保安全稳定的生产和运作[2-4]。FMEA方法旨在通过分析罗列潜在故障模式及其可能造成的影响，以实数1～10的形式预先估计不同故障模式在频度O、严重度S和不易探测度D三种风险因子下的实际表现情况，进而得到其风险优先值RPN，即RPN=O×S×D，针对不同风险优先值的故障模式采取不同程度的安全控制措施。虽然FMEA方法在安全评估方面具有较好效用，但是仍然存在一些不足[4]：①故障模式评估信息通常具有不确定性和不完整性，难以用实数直接表征；②并未考虑风险因子权重信息，与实际情况不符；③风险优先值计算模型值得商榷，易出现相同风险优先值，以致故障模式风险顺序难以判断，且信息融合过程不合理将造成信息丢失。

针对问题①，众多学者将模糊集理论运用于FMEA方法中。Song等[5]运用三角模糊数表征FMEA评估信息对故障模式进行风险评估；Ekmekçiolu等[6]提出基于梯形模糊数的FMEA风险评估方法；王晓暾等[7]运用语义变量刻画FMEA中专家信息的模糊性和不确定性；Chang[8]引入二元语义变量作为信息载体优化FMEA方法。与此同时，将模糊集理论与粗糙集理论、证据理论、软集理论等相结合表征评估信息的FMEA研究也屡见不鲜。Vahdani等[9]将置信结构和模糊理论相结合，提出基于模糊置信结构的FMEA方法；安相华[10]运用区间形式的模糊粗糙数有效处理FMEA专家评估信息的不确定性；王浩伦等[11]提出基于三角模糊软集的AND运算，并对FMEA中的故障模式进行风险排序。此外，Atanassov[12]在模糊集理论基础上提出直觉模糊集(Intuitionistic Fuzzy Set，IFS)理论，同时考虑隶属度、非隶属度和犹豫度3种信息，在不确定性的表达方面比模糊集更为灵活和实用，运用到FMEA方法中具有较好的效果[13]。

针对问题②，目前所运用的风险因子权重方法主要有主观赋权法、客观赋权法和综合赋权法。其中，主观赋权法最为普遍，一般通过改进层次分析法(Analytic Hierarchy Process, AHP)[6]和专家风险因子权重评估信息[9]得到，然而该方法过于依赖专家或决策者的经验判断，未充分考虑信息本身在权重确定中的作用。Emovon等[14]提出一种熵权法和方差法相结合的客观赋权法确定风险因子权重；Chang[15]在运用有序加权几何平均算子集结故障模式评估信息的同时，结合熵权最大化模型求解风险因子权重。综合赋权法同时集结主客观风险因子权重评估信息，较仅考虑单方面因素的赋权法更为准确，且可根据专家对评估信息的确定程度调整主客观权重比例，具有较强的灵活性和实用性。例如Song等[5]构建了一种专家评估法和熵权法相结合的综合赋权法确定风险因子权重。

针对问题③，FMEA本质上也可看作是一种多属性群决策问题，故与模糊理论相结合的折衷排序法( Vlsekriterijumska Optimizacija I Kompromisno Resenje, VIKOR)[10]、理想解相似度顺序偏好法(Technique for Order Preference by Similarity to Ideal Solution, TOPSIS)[5]、AHP[16]及决策实验和评价实验室(DEcision MAking Trial and Evaluation Laboratory, DEMATEL)[15]等多属性决策方法被广泛用于FMEA研究，以改进传统风险优先值的排序方法。然而，以上多属性决策方法决策方式单一，其排序鲁棒性尚待提高。Brauers[17]对多属性决策方法的鲁棒性进行了系统研究，提出结合两种不同决策方式的多属性决策方法优于单一决策方式多属性决策方法，结合3种不同决策方式的多属性决策方法优于仅结合两种不同决策方式的多属性决策方法，以此类推。此后，Brauers等[18]将全乘模型引入比例分析多目标优化(Multi-Objective Optimization by Ratio Analysis, MOORA)方法，进而提出全乘比例分析多目标优化(MOORA plus the full MULTIplicative form, MULTIMOORA)方法。MULTIMOORA方法的运算简便、强鲁棒性[19]等特点使其一经提出便被广泛运用于经济、天气和电子等决策研究领域[20]。

除上述不足之外，现有FMEA相关研究较少改进专家权重信息确定方法，基本为直接给定专家权重，这将影响风险排序结果的准确性。为解决该问题，本文提出一种基于直觉模糊全乘比例分析多目标优化(Intuitionistic Fuzzy MULTIMOORA, IF-MULTIMOORA)的FMEA风险评估方法，该方法运用语言变量同时表征专家对故障模式在风险因子下的实际表现和风险因子权重的评估信息，并转化为相应直觉模糊数；将多个专家依据其知识结构和领域经验划分为若干优先等级，利用直觉模糊优先加权平均(Intuitionistic Fuzzy Prioritized Weighted Averaging, IFPWA)算子对专家评估信息进行集结；通过专家评估法和偏差最大化模型法相结合的综合赋权法确定风险因子权重信息；改进MULTIMOORA方法相关步骤，提出直觉模糊背景下的IF-MULTIMOORA方法并对故障模式进行风险排序。最后，本文将所提FMEA方法应用于铁路线路维修风险评估，验证了其可行性和有效性。

1 相关概念

1.1 直觉模糊集

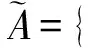
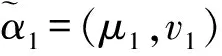
(1)

(2)

(3)

(4)

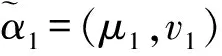
|π1-π2|)。

(5)

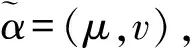
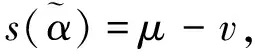
(6)

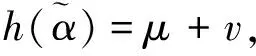
(7)

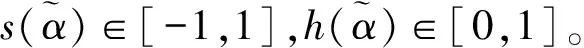
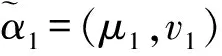
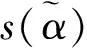
(8)

1.2 直觉模糊集成算子

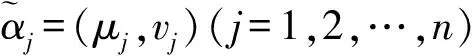
(9)

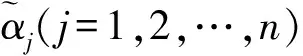
(10)

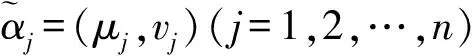
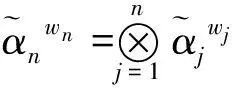
(11)

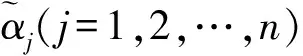
(12)

2 基于IF-MULTIMOORA的FMEA风险评估方法

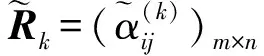
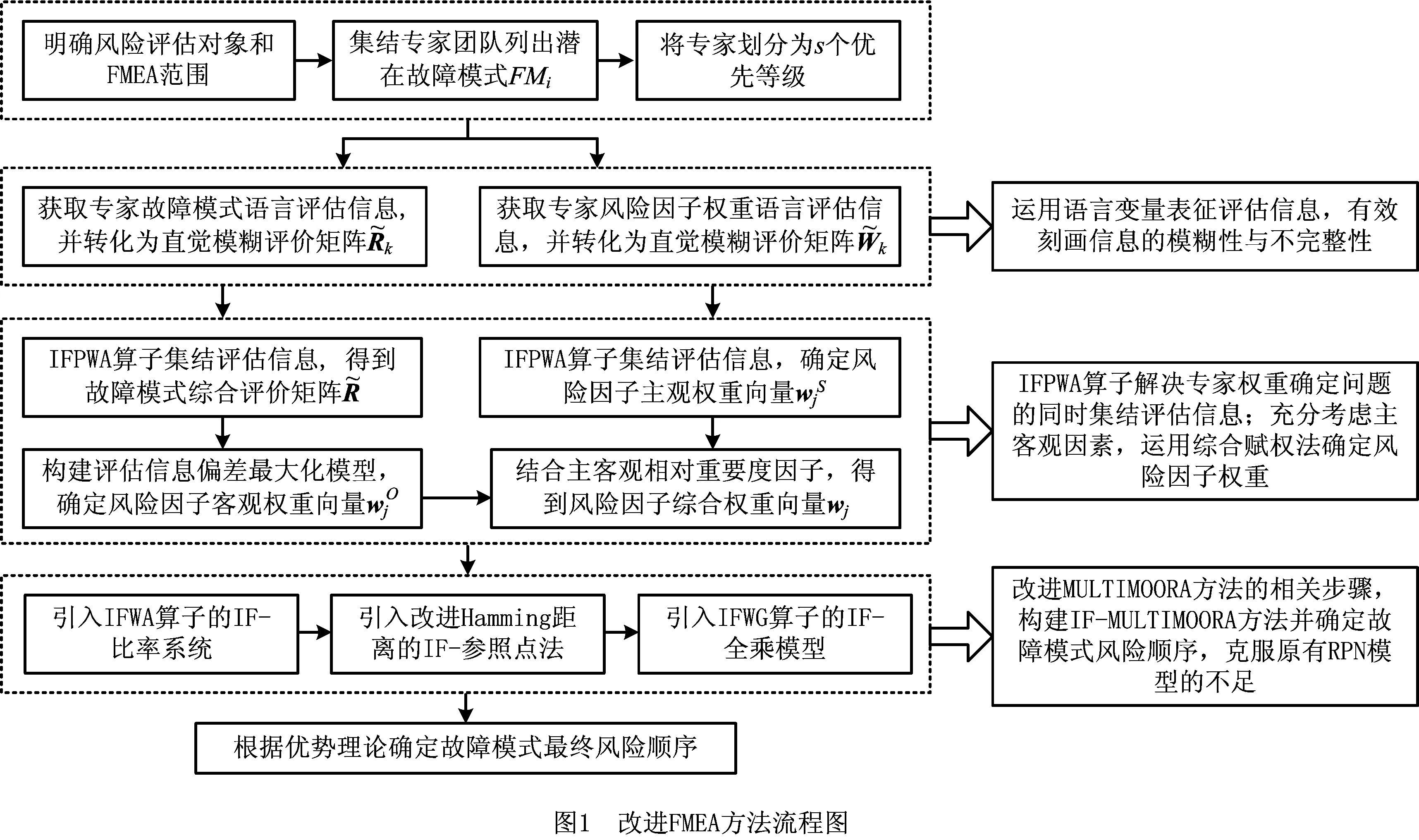
2.1 故障模式评估信息的集结

在实际情况中，安全管理人员可通过收集企业故障模式的发生频率、故障后果严重程度和故障检测率等历史数据对故障模式进行风险评估和管理，然而现有大多数企业的相关事故数据并不完整，因此本文将采用专家参考历史数据对故障模式进行评估的方法得到风险评估信息。

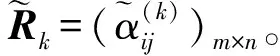
(13)

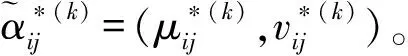
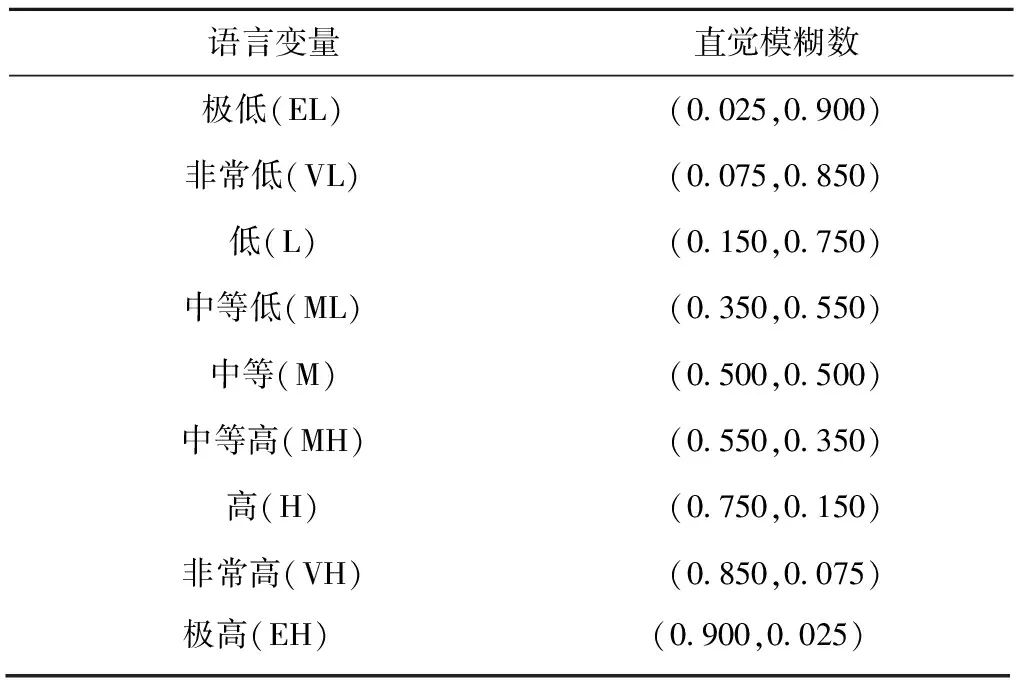
表1 故障模式语言变量等级

在群体评估信息集结过程中，确定专家权重为关键步骤之一，而现有FMEA相关研究中较少涉及此类问题，基本为直接给定专家权重，这对研究结果准确性有一定的影响。虽然采用主观赋权法难以准确确定专家权重，但是依据专家知识结构和领域经验的不同，确定其优先等级较为简单可行，文献[26]在Yager[27]构建的优先平均算子基础上定义的IFPWA算子运用到此类问题信息集结中效果较好。

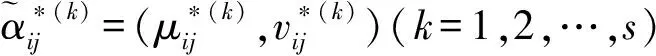
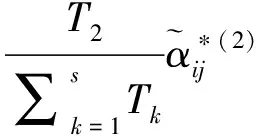
(14)

为直觉模糊优先加权平均算子。

(15)

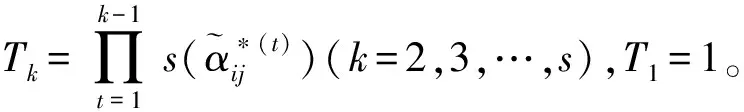
2.2 风险因子权重的确定

传统FMEA风险评估过程中并未考虑风险因子权重信息，将频度、严重度和不易探测度视作同等重要显然与实际情况不符，导致最终故障模式风险顺序不够准确。然而，风险因子权重较难直接确定，故众多权重计算方法被运用于FMEA风险因子权重确定，主要有主观赋权法、客观赋权法和综合赋权法，其中综合赋权法因能同时考虑主客观因素，克服仅考虑单方面方法的局限性，而被众多学者所采用。本文将通过专家评估法和偏差最大化模型法相结合的综合赋权法，从主客观两个方面确定风险因子综合权重，克服传统FMEA未考虑风险因子权重的不足。

(16)

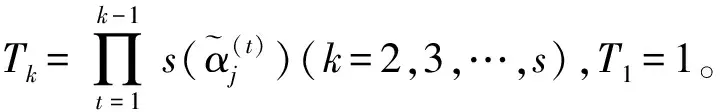
(17)

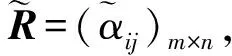
s.t.

(18)

结合Lagrange方法求解该模型，构造Lagrange函数

(19)

对式(19)分别求偏导数，并使下式成立：

(20)

得出风险因子客观权重最优解并做归一化处理，即

(21)

(22)

式中φ1和φ2分别为主观和客观权重的相对重要度，0≤φ1,φ2≤1，φ1+φ2=1，j=1,2,…,n。

2.3 基于IF-MULTIMOORA的故障模式风险排序

MULTIMOORA方法首先需要将评估信息标准化，消除不同属性量纲之间的差异，进而通过相关运算分别得到比率系统、参照点法和全乘模型下的故障模式风险顺序，在此基础上依据优势理论[19]确定故障模式的最终风险排序。然而，传统MULTIMOORA方法仅适用于实数背景，对于信息载体为直觉模糊数的MULTIMOORA决策方法，相关步骤必须进行一定的适应性改进，分别将IFWA算子和IFWG算子引入比率系统和全乘模型的故障模式信息融合，避免信息丢失；计算参照点法中故障模式信息与参照点之间的改进Hamming距离，提升排序鲁棒性，进而构建一种IF-MULTIMOORA方法来确定故障模式的风险顺序。

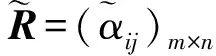
(23)

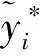
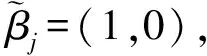
(24)

其中，当γ=1和γ=2时，定义距离分别为绝对距离和欧式距离，但两种距离鲁棒性都有待提高。文献[17]指出，基于该距离的优化排序问题鲁棒性随γ值的增大而增强，故选取γ→∞，定义距离称为Tchebycheff度量，即

(25)

结合式(5)，引入风险因子权重向量wj={w1,w2,…,wn}作为显著性系数计算FMi在不同风险因子下与参照点之间的Tchebycheff距离，即

(26)

故障模式的Tchebycheff距离越大，风险排序越高。

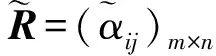
(27)

步骤4优势理论。IF-MULTIMOORA方法由IF-比率系统、IF-参照点法和IF-全乘模型3部分组成，即存在3种故障模式风险顺序，且具有同等重要程度。结合优势理论，两两比较步骤1～步骤3得出的各故障模式下3种风险顺序所构成的三元数组中的广义优势关系，确定故障模式最终风险排序。

3 案例分析

3.1 铁路线路维修风险评估

铁路运输是我国重要的服务产业，关系到人民和企业的生命财产，保证安全是其首要任务，而铁路线路是铁路运输的基础，其安全维修将对全路安全有重大影响。因此，铁路线路维修风险评估具有重要的实际意义。

铁路线路维修分为综合维修、日常保养和临时补修，庞旭青[30]通过系统分析，确定了铁路线路日常保养和临时补修中的16个潜在故障模式，即道岔无表示(FM1)、道岔挤岔(FM2)、水漫铁路道床(FM3)、隧道内铁件锈蚀(FM4)、列车刮撞机具(FM5)、道岔信号红光带(FM6)、钢轨传输信号中断(FM7)、连接零件连续失效(FM8)、接头木岔枕失效(FM9)、列车晃车(FM10)、山体掩埋铁路(FM11)、无计划施工(FM12)、列车撞人(FM13)、护轨螺栓不全(FM14)、线桥偏心(FM15)和铁路胀轨跑道(FM16)。本节将在该研究的基础上，运用基于IF-MULTIMOORA的FMEA方法对16个潜在故障模式进行风险评估。

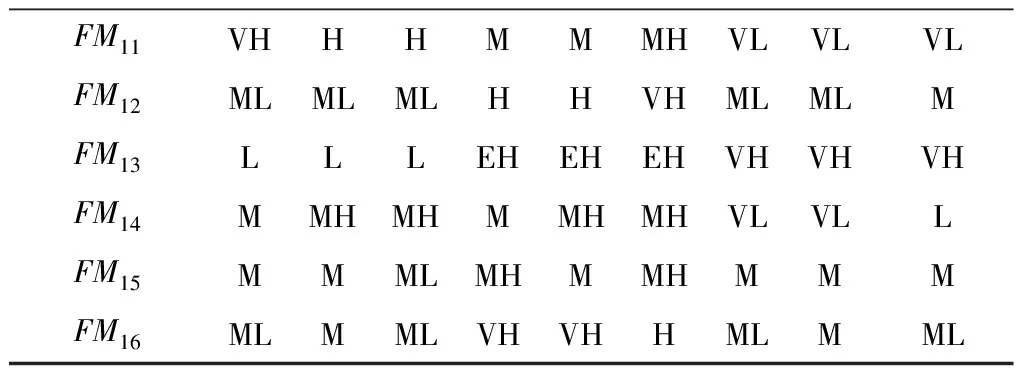
续表2

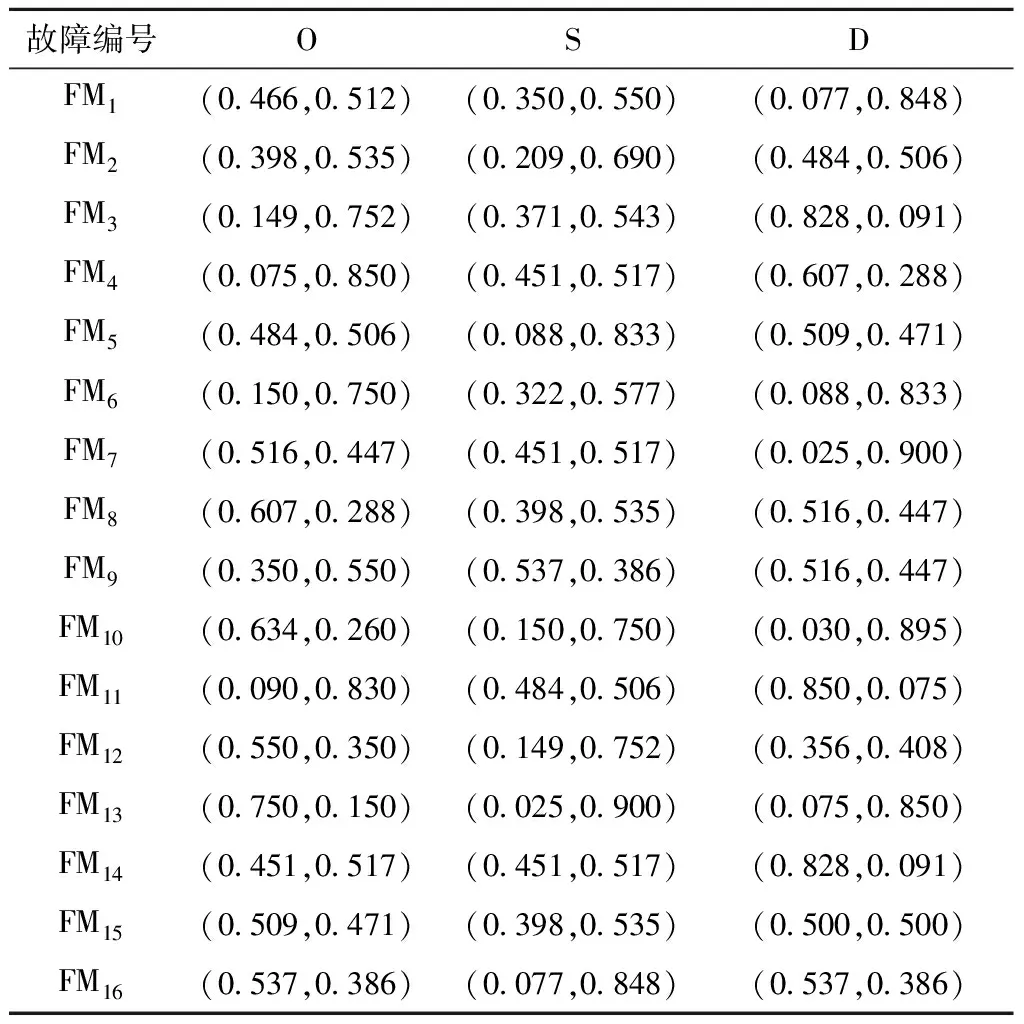
表3 故障模式直觉模糊综合评价矩阵

表4 专家评估法相关参数

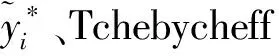
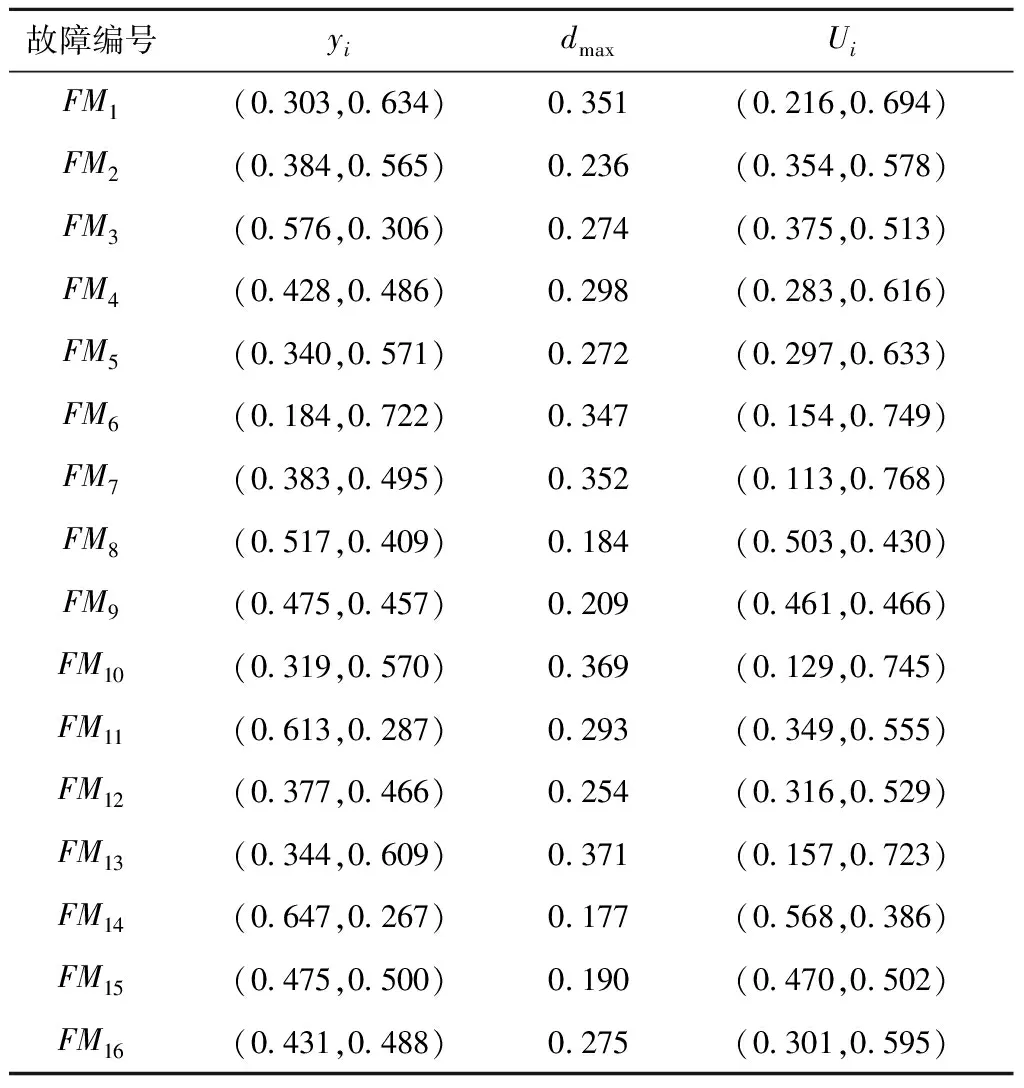
表6 IF-MULTIMOORA方法相关参数

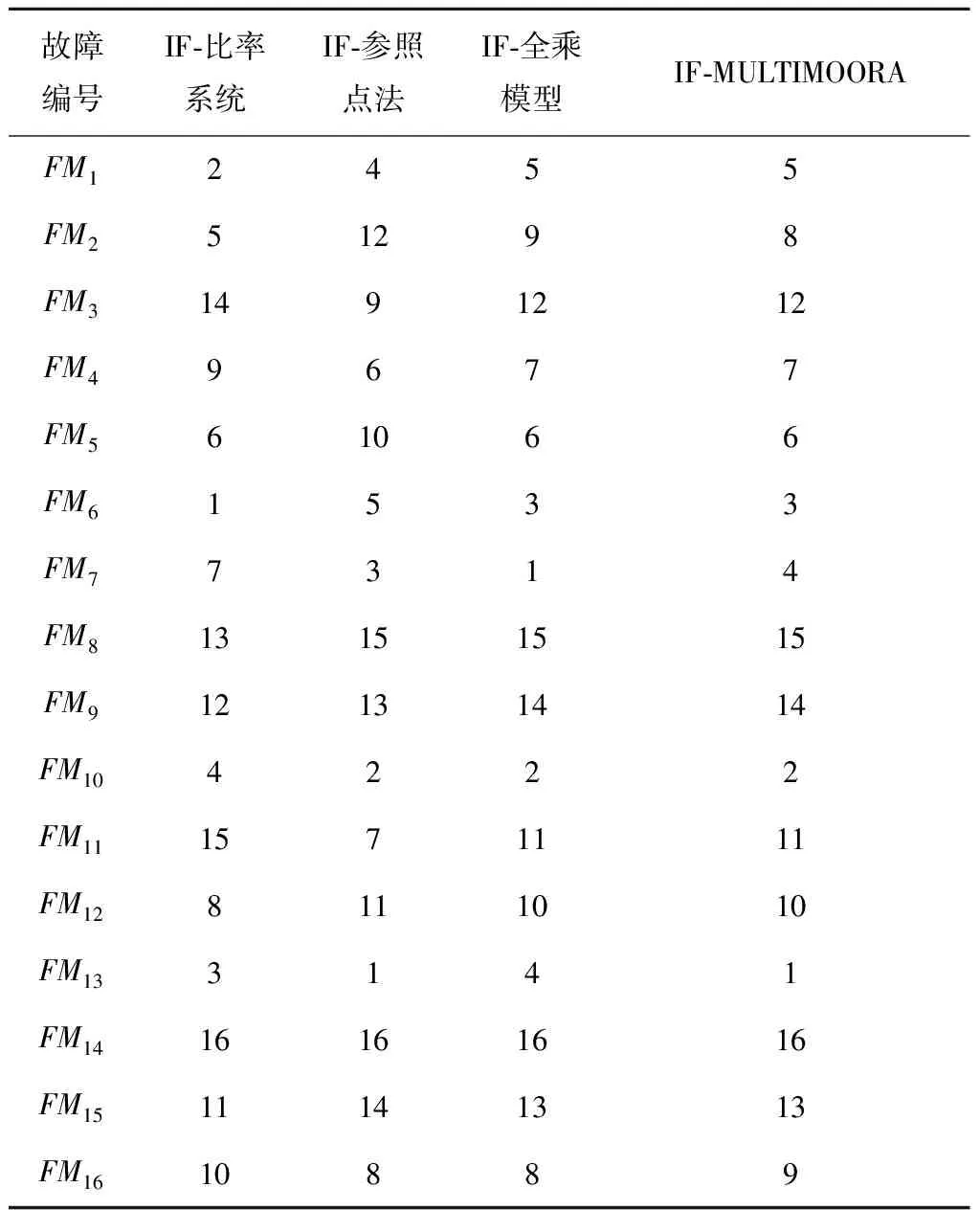
表7 IF-MULTIMOORA方法故障模式风险顺序

目前，铁路交通事故依据人员伤亡数量、经济损失和中断行车时间等指标划分为特别重大事故、重大事故、较大事故和一般事故等若干等级，如表8所示。铁路线路维修具有劳动强度高、安全隐患多、受天气环境影响大和直接影响铁路行车等工作特点，因此事故率极高。在实际铁路线路维修工作中，维修人员按计划以小组为单位在车站内及车站间线路上进行检修作业，当出现防护人员与行车人员联控不当、维修人员撤离股道不及时或者天气环境恶劣等情况时，就有可能导致FM13(即列车撞人)发生，造成检修人员伤亡、中断行车和干扰正常旅客和货物运输的严重后果，发生较高等级的铁路交通事故。同时，因为铁路沿线生活环境较差、维修作业强度较高、露天与高空作业频繁，以及可能出现的桥梁与隧道作业环境，容易导致维修人员疏于瞭望防护，造成列车撞人事故不易探测，所以实际工作中FM13风险排序最高，与本文案例结果一致。在铁路线路维修安全管理中，应从人、机、环境和管理4个方面分析确定FM13的控制措施并加以实施，从而保障维修工作的安全性。

表8 铁路交通事故等级

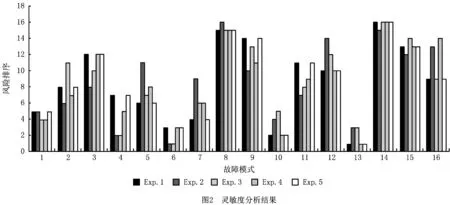
3.2 灵敏度分析

依据表9中风险因子权重的变化信息，对本文提出的FMEA方法的风险评估结果进行灵敏度分析，其中Exp.1中的风险因子权重信息为综合赋权法求得的原始权重，Exp.2～Exp.5为其他可能出现的风险因子权重，分别得到16个故障模式的风险顺序如图2所示。由图2可以看出，风险因子权重的变化对故障模式最终风险排序有巨大影响，例如当风险因子频度的权重较高、而风险因子不易探测度和严重度的权重较低时，FM13的风险顺序发生了变化，从第1位变成第3位，这是由于FM13在实际铁路线路维修中的发生频率相对较低，若侧重考虑频度因素，将降低其风险顺序。因此，选取合适的方法确定风险因子权重信息显得尤为重要，而本文提出的综合赋权法充分考虑专家意见和评估信息本身在权重确定中的作用，使风险顺序更为贴近实际。此外，在本文提出的综合赋权法中，φ1和φ2的取值可由决策者确定，当FMEA专家团队对风险因子权重信息不太确定或者难以评估时，应假设φ1<φ2；当FMEA专家团队对风险因子权重的评估信息较为确定时，应假设φ1>φ2。

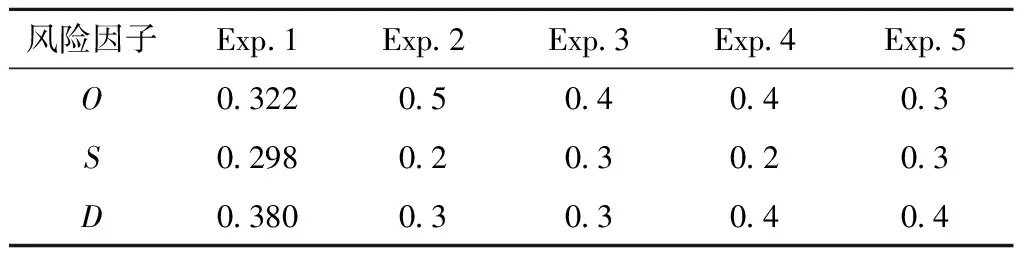
表9 灵敏度分析中的风险因子权重

3.3 对比分析

为验证本文所提FMEA方法的有效性，将本文案例的故障模式风险排序结果与文献[30]提出的改进风险优先值方法、文献[19]提出的实数型MULTIMOORA方法和文献[31]提出的直觉模糊TOPSIS(IF-TOPSIS)方法计算得出的故障模式风险排序进行对比，如表10所示。基于表10中的结果，可以看出本文所提FMEA方法相对于其他方法的优越性。

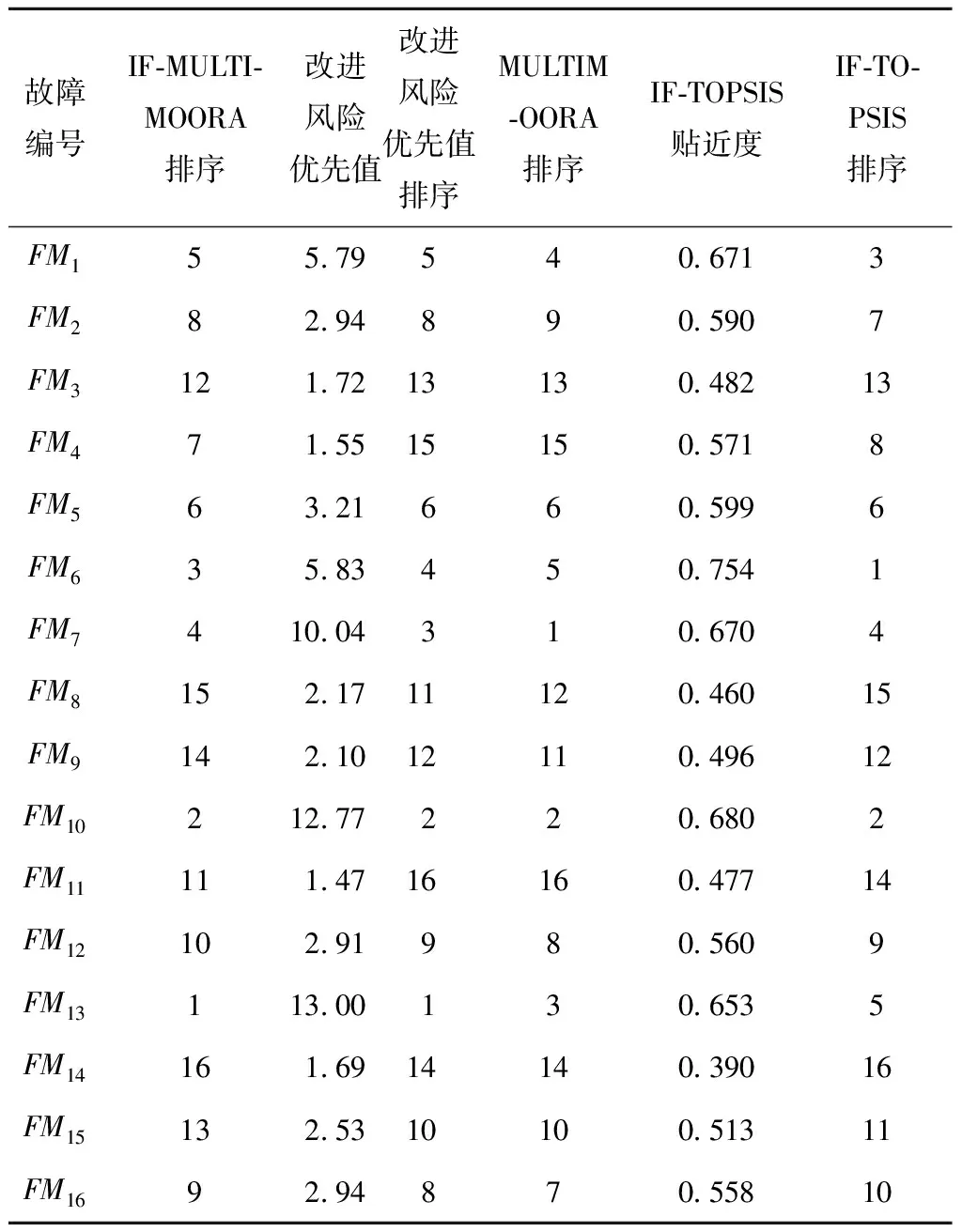
表10 故障模式风险排序比较

首先，与改进风险优先值方法相比，大多数的故障模式风险顺序不变，存在少数故障模式出现跳跃式变化(如FM11)，这是由于：①文献[30]提出的改进风险优先值方法未考虑故障模式的频度信息，默认频度评估值为1导致信息不完整；②采用1～10的实数形式表征故障模式评估信息，未能有效处理评估信息的模糊性；③均等分配风险因子权重，所得故障模式风险优先值与实际情况存在出入；④信息融合方式为简单的评估信息相乘，易出现相同的风险优先值(如FM2和FM16)以致风险顺序难以判断，且存在信息损失现象。

其次，实数型MULTIMOORA方法的故障模式风险排序结果与本文方法也存在些许差异，例如故障模式FM7(钢轨传输信号中断)变为风险顺序最高，在实际情况中，钢轨传输信号中断故障模式虽难以探测，但发生频率相对较低，且造成的影响一般为影响工务设备的使用寿命，不会导致较高等级的铁路交通事故，因此FM7在铁路线路维修中是一种风险程度较高的故障模式，但风险程度最高的依然是FM13。造成这些差异的原因除了实数在刻画评估信息不确定性上效用不足以外，还有IF-MULTIMOORA方法在原有比率系统、参照点法和全乘模型3个步骤中分别引入IFWA算子、改进Hamming距离和IFWG算子优化信息集结过程，突出风险因子权重对风险顺序影响的作用。

最后，可以看出IF-TOPSIS方法得到的故障模式风险顺序与本文方法差别最为明显，这是由于IF-MULTIMOORA方法所得故障模式风险顺序是在IF-比率系统、IF-参照点法和IF-全乘模型3种决策方法所得排序结果的基础上依据优势理论确定的，排序接近的故障模式风险顺序在两种方法之下会出现一定差异。其中，IF-参照点法仍采用传统参照点法，并未运用TOPSIS方法，原因为TOPSIS方法决策中与正理想值距离更近的故障模式可能同时与负理想值距离也更近，不能全面反映故障模式的风险程度，影响决策结果的准确性[32]。同时，文献[17]提出衡量多属性决策方法鲁棒性的6个条件，且得到了在此基础之上结合多种决策方式的多属性决策方法的鲁棒性优于单一决策方式的多属性决策方法的结论。因此，本文方法较IF-TOPSIS方法所得的排序结果更为科学，且鲁棒性有所提高。

总而言之，4种方法得出的故障模式风险排序结果中，FM1，FM5，FM6，FM7，FM10和FM13都为风险排序最高的6种，只是具体风险顺序各有不同，而本文方法在FMEA过程中的每一步都进行了一定优化，所得结果可为决策者提供更精确的风险管理参考依据，由此证实了本文方法的可行性和有效性。

4 结束语

传统FMEA风险评估方法虽然已被广泛运用，但是仍存在若干不足。为了提升FMEA过程的准确性和科学性，本文提出一种基于IF-MULTIMOORA的FMEA风险评估方法。相比于现有的FMEA方法，本文方法具有以下优势：①运用语言变量表征评估信息，较实数更符合实际思维习惯，并将语言评估信息转化为相应的直觉模糊数，从而有效处理专家评估信息的不确定问题，保留信息的完整性；②根据专家知识结构和领域经验的不同赋予专家不同的优先等级，运用IFPWA算子集结专家评估信息，解决专家权重确定问题的同时避免信息融合中信息的丢失；③提出由专家评估法和偏差最大化模型法组成的综合赋权法确定风险因子权重信息，同时考虑主客观因素，较仅考虑单方面因素的赋权法更为准确；④分别引入IFWA算子、改进Hamming距离和IFWG算子改进MULTIMOORA方法中的IF-比率系统、IF-参照点法和IF-全乘模型步骤，提出直觉模糊背景下的IF-MULTIMOORA方法并对故障模式进行风险排序，提升了已有FMEA结果鲁棒性。最后，以铁路线路维修FMEA风险评估为例，证实了该方法的可行性和有效性。

随着企业信息化程度以及对于风险管理的重视程度不断提高，如何将事故数据转化为相应评估信息形式，以及在事故数据或者专家评估信息缺失的情况下进行相关研究，将是未来风险评估的研究重点。

[1] KUTLU A C, EKMEKÇIOLU M. Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy AHP[J]. Expert Systems with Applications,2012,39(1):61-67.

[2] LIU Huchen, LIU Long, LI Ping. Failure mode and effects analysis using intuitionistic fuzzy hybrid weighted Euclidean distance operator[J]. International Journal of Systems Science,2014,45(10):2012-2030.

[3] SONG Wenyan, MING Xinguo, WU Zhenyong, et al. A rough TOPSIS approach for failure mode and effects analysis in uncertain environments[J]. Quality & Reliability Engineering International,2014,30(4):473-486.

[4] LIU Huchen, LIU Long, LIU Nan. Risk evaluation approaches in failure mode and effects analysis:A literature review[J]. Expert Systems with Applications,2013,40(2):828-838.

[5] SONG Wenyan, MING Xingguo, WU Zhenyong, et al. Failure modes and effects analysis using integrated weight-based fuzzy TOPSIS[J]. International Journal of Computer Integrated Manufacturing,2013,26(12):1172-1186.

[7] WANG Xiaotun, XIONG Wei. Risk evaluation method in FM-EA based on dependent linguistic ordered weighted geometric operator[J]. Journal of Zhejiang University:Engineering Science,2012,46(1):182-188(in Chinese).[王晓暾,熊 伟.基于DLOWG算子的FMEA风险评估方法[J].浙江大学学报:工学版,2012,46(1):182-188.]

[8] CHANG K H. A more general risk assessment methodology using a soft set-based ranking technique[J]. Soft Computing,2014,18(1):169-183.

[9] VAHDANI B, SALIMI M, CHARKHCHIAN M. A new FMEA method by integrating fuzzy belief structure and TOPSIS to improve risk evaluation process[J]. International Journal of Advanced Manufacturing Technology,2015,77(1/2/3/4):357-368.

[10] AN Xianghua, YU Jingbo, CAI Weiguo. Fuzzy rough FMEA evaluation method based on hybrid multi-attribute decision and correlative analysis[J]. Computer Integrated Manufacturing Systems,2016,22(11):2613-2621(in Chinese).[安相华,于靖博，蔡卫国.基于混合多属性决策和关联分析的模糊粗糙FMEA评估方法[J].计算机集成制造系统,2016,22(11):2613-2621.]

[11] WANG Haolun, XU Xiangbin, GAN Weihua. Risk evaluation method in FMEA based on triangular fuzzy soft set[J]. Computer Integrated Manufacturing Systems,2015,21(11):3054-3062(in Chinese).[王浩伦,徐翔斌,甘卫华.基于三角模糊软集的FMEA风险评估方法[J].计算机集成制造系统,2015,21(11):3054-3062.]

[12] ATANASSOV K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets & Systems,1986,20(1):87-96.

[13] ZHAO Hao, YOU Jianxin, LIU Huchen. Failure mode and effect analysis using MULTIMOORA method with continuous weighted entropy under interval-valued intuitionistic fuzzy environment[J]. Soft Computing,2016,21(18):1-13.

[14] EMOVON I, NORMAN R A, ALAN J M, et al. An integrated multicriteria decision making methodology using compromise solution methods for prioritising risk of marine machinery systems[J]. Ocean Engineering,2015,105(10):92-103.

[15] CHANG K H. Evaluate the orderings of risk for failure problems using a more general RPN methodology[J]. Microelectronics Reliability,2009,49(12):1586-1596.

[16] LLANGKUMARAN M, SHANMUGAM P, SAKTHIVEL G, et al. Failure mode and effect analysis using fuzzy analytic hierarchy process[J]. International Journal of Productivity & Quality Management,2014,14(3):296-313.

[17] BRAUERS W K M. Project Management for a country with multiple objectives[J]. Czech Economic Review,2012,6(1):80-101.

[18] BRAUERS W K M, ZAVADSKAS E K. Project management by MULTIMOORA as an instrument for transition economies[J]. Technological & Economic Development,2010,16(1):5-24.

[19] BRAUERS W K M, ZAVADSKAS E K. Robustness of MULTIMOORA:a method for multi-objective optimization[J]. Informatica,2012,1(1):1-25.

[20] TOMAS B, ALVYDAS B. A survey on development and applications of the multi-criteria decision making method MULTIMOORA[J]. Journal of Multi-Criteria Decision Analysis,2014,21(3/4):209-222.

[21] XU Zeshui, YAGER R R. Some geometric aggregation operators based on intuitionistic fuzzy sets[J]. International Journal of General Systems,2006,35(4):417-433.

[22] XU Yongjie, SUN Tao, LI Dengfeng. Intuitionistic fuzzy prioritized OWA operator and its application in multi-criteria decision-making problem[J].Control and Decision,2011,26(1):129-132(in Chinese).[徐永杰,孙 涛,李登峰.直觉模糊POWA算子及其在多准则决策中的应用[J].控制与决策,2011,26(1):129-132.]

[23] XU Zeshui. Intuitionistic fuzzy aggregation operators[J]. IEEE Transactions on Fuzzy Systems,2008,14(6):1179-1187.

[24] CHIN K S, WANG Y M, GARY K K P, et al. Failure mode and effects analysis using a group-based evidential reasoning approach[J]. Computers & Operations Research,2009,36(6):1768-1779.

[25] LIU Huchen, YOU Jianxin, LI Ping, et al. Failure mode and effect analysis under uncertainty:an integrated multiple criteria decision making approach[J]. IEEE Transactions on Reliability,2016,65(3):1380-1392.

[26] YU Dejian. Intuitionistic fuzzy prioritized operators and their application in multi-criteria group decision making[J]. African Journal of Business Management,2013,19(1):1-21.

[27] YAGER R R. Prioritized aggregation operators[J]. International Journal of Approximate Reasoning,2008,48(1):263-274.

[28] XU Zeshui. A deviation-based approach to intuitionistic fuzzy multiple attribute group decision making[J]. Group Decision & Negotiation,2010,19(1):57-76.

[29] ZHANG Xin, JIN Fang, LIU Peide. A grey relational projection method for multi-attribute decision making based on intuitionistic trapezoidal fuzzy number[J]. Applied Mathematical Modelling,2013,37(5):3467-3477.

[30] PANG Xuqing. Safety risk management of railway line maintenance based on FMEA method[J]. Chinese Railways,2012(6):48-50(in Chinese).[庞旭青.基于FMEA方法的铁路线路维修安全风险管理研究[J].中国铁路,2012(6):48-50.]

[31] BORAN F E, GENÇ S, KURT M, et al. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method[J]. Expert Systems with Applications,2009,36(8):11363-11368.

[32] HUA Xiaoyi, TAN Jingxin. Revised TOPSIS method based on vertical projection distance-vertical projection method[J]. System Engineering—Theory & Practice,2004,24(1):114-119(in Chinese).[华小义,谭景信.基于“垂面”距离的TOPSIS法—正交投影法[J].系统工程理论与实践,2004,24(1):114-119.]