基于统计模拟法的未来空域窗全航路毁伤概率仿真
2018-03-19王成飞张渝缘石章松
王成飞, 张渝缘, 石章松
(1.解放军91655部队, 北京 100036;2.海军工程大学电子工程学院, 湖北 武汉 430033)
在对高超声速目标进行拦截时,由于高超声速目标运动速度快,跟踪滤波器对目标的定位跟踪能力有限,使得提前点的计算精度下降,传统的集火射击方法对目标的毁伤概率变低。为克服集火射击的缺陷,未来空域窗射击体制应运而生,其窗主要是以预测目标未来点为中心,朝配置的多个瞄准点进行射击,即以面射击的方式,提高对来袭目标的毁伤概率。
国内对未来空域窗毁伤概率的研究中,文献[1]提出了未来空域窗毁伤概率的解析计算方法,文献[2]按照高炮点射过程,给出了一种计算毁伤概率的方法,但没有考虑目标跟踪滤波,误差处理等问题。文献[3]结合了具体高炮系统的跟踪分系统、火控分系统和火力分系统进行分析,但对未来空域窗的配置没有进行详细说明。
本文结合未来空域窗的构造方法,通过对典型高超声速目标航迹建模、滤波跟踪、误差处理、空域窗配置、相遇解算、判断毁伤等步骤进行分析,计算未来空域窗全航路毁伤概率,并与集火射击体制下的毁伤概率进行对比,其仿真结果具有一定可信性。
1 基于统计模拟法的未来空域窗全航路毁伤概率计算流程
在未来空域窗全航路射击方法研究中,最有效最直接的方法是进行射击实验,然而,受实验条件、经济因素等制约,多次进行大规模的射击实验几乎是不可能的。本文针对未来空域窗全航路毁伤概率问题,通过对典型反舰导弹运动航路仿真建模,对目标进行滤波跟踪,同时根据滤波结果和误差,对未来空域窗最优射击时机进行选择,对速度误差进行近似处理,求出既定毁伤概率情况下的射弹数量,求解配置未来空域窗瞄准点,并依据瞄准点位置解算射击诸元,判断是否毁伤。具体顺序如图1所示。
通过统计模拟法对未来空域窗全航路毁伤概率仿真时,首先要对典型反舰导弹航迹进行仿真建模,并把生成的航路真实值叠加系统误差和量测误差。当目标进入小口径舰炮拦截区域时,对舰炮射弹误差和目标量测误差进行处理,同时对速度误差进行等效处理,判断一次射击时间内最优射击时机,确定最优射击时机后,求解不同约束条件下的射弹数量,并依据处理后的迎弹面上的误差,对未来空域窗的瞄准点进行配置。同时,计算到达各瞄准点时的射击诸元,通过外推弹道不断计算射弹的空间位置,并判断射弹与目标是否相遇,统计出命中弹数,再根据命中击毁率计算毁歼概率,毁歼概率平均值即为目标毁歼概率。
2 未来空域窗全航路仿真的关键步骤
2.1 可行性分析
不同于集火射击体制,未来空域窗射击体制是针对相遇提前点,依据目标的分布密度特性,对未来空域窗瞄准点进行配置,由多门舰炮向各个瞄准点发射,形成未来空域窗,使窗内的弹丸散布密度达到一定水平,从而提升对目标的拦截概率,在实际射击过程中,针对已确定的发射提前点,通过对目标量测误差,射弹不相关、相关误差等各项误差进行综合处理,将误差分别投影至目标与射弹相遇的迎弹面上,计算在迎弹面上的误差分布特性,并根据迎弹面上的误差特性,配置未来空域窗的瞄准点,再由多门舰炮对瞄准点进行射击,实现对目标的有效拦截。因此,采用未来空域窗射击体制是可行的。
2.2 速度误差处理
在以往的未来空域窗瞄准点配置过程中,一般认为目标提前点的误差特性与观测点的误差特性不发生变化,但实际情况中,目标由观测点到达提前点具有一定的时间间隔,由于目标速度的观测值存在一定误差,使得目标提前点的误差特性往往不同于观测点的误差特性,因此需要建立考虑目标速度误差的未来空域窗瞄准点配置方法。
通常,若不考虑速度误差情况下,对射弹误差特性分析时,会在目标与射弹的迎弹面上进行目标分布密度分析,通过对射弹不相关误差、相关误差和目标量测误差的综合处理,并进行坐标系之间的转化,将射弹的等效误差特性转化到迎弹面上,如图2所示。
其中,E1X1、E1X2表示射弹散布在X1、X2轴上的不相关误差,E2X1、E2X2表示射弹散布在X1、X2轴上的相关误差。
以舰艇位置为原点,Y轴指向舰艇航向,Z轴垂直原点所在水平面并指向天顶,X轴垂直于YZ平面,建立地理坐标系O-XYZ。X3轴指向炮弹速度Vd与目标速度Vt矢量差,X1轴垂直于X3并在X3的铅垂面内,X2轴垂直于X1X3平面,建立迎弹面坐标系Od-X1X2X3,如图3所示。
在迎弹面坐标系内,假设某时刻目标真实速度为Vt=(Vtx2,Vtx1,Vtx3),观测速度为Vtc=(Vtcx2,Vtcx1,Vtcx3)。射弹速度为Vd=(Vdx2,Vdx1,Vdx3),目标速度误差为ΔVt=(ΔVtx2,ΔVtx1,ΔVtx3),服从均值为零,方差为(σvtx2,σvtx1,σvtx3)的正态分布。目标位置为Xt=(X2t,X1t,X3t),目标位置量测误差为ΔXt=(ΔX2t,ΔX1t,ΔX3t),服从均值为零,方差为(σx2,σx1,σx3)的正态分布。射弹不相关误差概率误差与相关误差概率误差比为(εx2,εx1),忽略观测提前点和实际提前点射弹速度变化和迎弹面方向变化,建立相遇模型如图4所示。
图中,T′表示某时刻观测的目标位置,T表示实际目标位置,Odc表示通过计算得到的相遇提前点,Od表示实际相遇提前点,为方便计算,假设在迎弹面内,目标与射弹的相对运动为匀速直线运动,则有
Dx3=(Vd-Vtx3)t
(1)
Dx3c=(Vd-Vtx3c)tc
(2)
式中,Dx3表示目标与我舰的实际相对距离,Dx3c表示目标与我舰的观测的相对距离。由于目标距离舰艇较远,可近似认为Dx3c=Dx3+ΔX3t,因此联立式(1)和(2)可得
(3)
为方便分析,假设实际相遇提前点的改变为迎弹面上相遇提前点位置变化,如图5所示。
在迎弹面内,相遇提前点的位置变化为:
Δx2=Vtcx2tc-Vtx2t=Vtcx2Δt+ΔVtx2t
=Vtcx2Δt+ΔVtx2(tc+Δt)
(4)
Δx1=Vtcx1tc-Vtx1t=Vtcx1Δt+ΔVtx1t
=Vtcx1Δt+ΔVtx1(tc+Δt)
(5)
经过上面分析,可以建立考虑速度误差的未来空域窗射击毁伤概率模型为

dx1dX3tdΔVtx1dΔVtx2dΔVtx3
(6)
其中,h(x2,x1)为弹丸散布密度函数,为:
(7)
相关误差在迎弹面上的概率密度函数为:
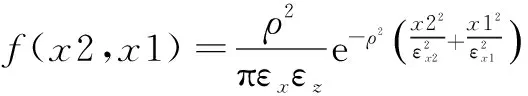
(8)
而fx3t(X3t)为目标位置误差在X3轴上的概率密度:

(9)
g(ΔVtx1ΔVtx2ΔVtx3)为目标速度误差概率密度函数:
g(ΔVtx1ΔVtx2ΔVtx3)=
(10)
在实际情况中,在瞄准点配置过程中,由于式(6)的计算量太大,不满足瞄准点配置实时性要求,因此,需要对其进行简化处理。
对式(3)进行近似处理:
(11)
可知,时间误差Δt服从均值为零,方差为σΔt的正态分布。其中
(12)
同理,对式(4)和(5)进行化简,可得:
Δx2=Vtcx2tc-Vtx2t=Vtcx2Δt+ΔVtx2t
≈Vtcx2Δt+ΔVtx2tc
(13)
Δx1=Vtcx1tc-Vtx1t=Vtcx1Δt+ΔVtx1t
≈Vtcx1Δt+ΔVtx1tc
(14)
(15)
(16)
由于相遇提前点的变化将会导致射弹整体位置的变化,因此可将相遇提前点的误差看作射弹的相关误差进行处理。将射弹相关误差和相遇提前点误差综合处理,得到考虑速度误差的射弹相关误差,从而对未来空域窗的瞄准点进行配置。
2.3 命中判断
在进行全航路未来空域窗毁伤概率仿真时,需要对射弹是否命中目标进行判断,通常,由于高超声速目标运动速度快,为了简化计算,可近似认为射弹和目标在相遇前都作匀速直线运动,根据弹着偏差的统计特征随机生成弹着误差,并可得到真实的弹着点为
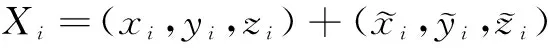
(17)

Xi(t)=Xi+tVd
(18)
相应的,目标航路可表示为
Xt(t)=Xt+tVt
(19)
因此有射弹与目标的距离偏差
Di(t)=|Xi(t)-Xt(t)|
(20)
当距离偏差最小的时刻有:
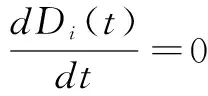
(21)
此时目标与射弹距离最小,目标与射弹的相对位置为Dimin。
In this paper, the electrical system operating status includes normal mode and fault mode. In the normal mode, the two main generators work properly, auxiliary electricity device and battery does not work; in the fault mode, the system has three main operating conditions.
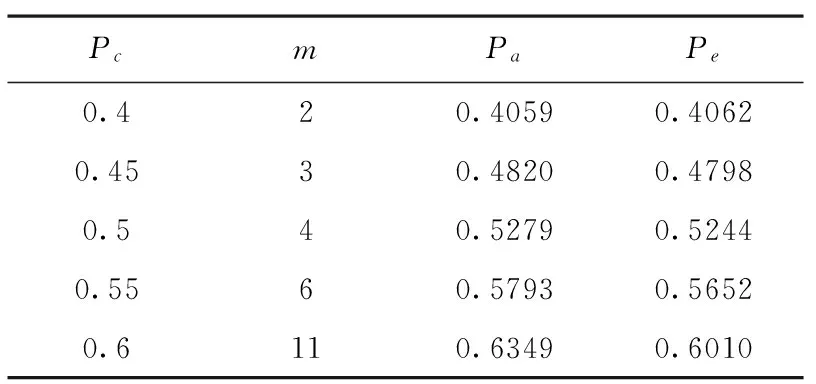
将Dimin投影到迎弹面,得到其在迎弹面上的分量为Diminx2、Diminx1,目标尺寸在迎弹面上的等效半长为S、L,若有
Diminx2 (22) 则认为可以命中。 依据未来空域窗射击的实际情况,设定目标速度Vt=2000m/s,炮弹速度Vd=1000m/s,跟踪器采样频率100Hz,观测距离和观测距变率随机误差均方差50m;观测方位角、高低角随机误差均方差5mrad;观测方位角、高低角变化率随机误差均方差5mrad/s。系统射击误差高度、方向不相关误差均方差为1mil、2mil,相关误差均方差为2mil、2mil。未来空域窗配置瞄准点数量n=30,目标等效命中面积B=1.5m,L=0.5m。 设以我舰为坐标原点,反舰导弹在三维空间内进行机动,航路特征为典型高速反舰导弹攻击航路。其末端航路为在距离我舰40km处开始降高,至距海平面60m处,平飞4s后开始进入比例引导阶段对我舰进行打击。其具体航路如图6所示。 假设跟踪器在反舰导弹距我舰40km处对目标进行跟踪,跟踪时间20s,分别进行100次蒙特卡洛仿真,其各方向滤波结果如图7-10所示。 获得目标的位置信息X、Y、Z,速度信息Vx、Vy、Vz,位置误差均方差Px、Py、Pz,速度误差均方差Pvx、Pvy、Pvz如表1所示。 表1 滤波误差结果 假设在第20s时目标进入我舰小口径炮打击范围,跟踪器滤波得到目标位置方向量测误差均方差均值为σx=2.7m、σy=4.3m、σz=2.2m,速度误差均方差均值为σvx=5.8m、σvy=4.8m、σvz=3.7m。规定一次射击时间为1s,不同射击时机下中间函数R值变化如表2所示。 表2 不同射击时机下的目标函数值 依据未来空域窗最优射击时机选取原则,当R值最大时,为最优射击时机,因此选择在t=21s时对反舰导弹进行打击。 假设配置瞄准点数目n=30,由于时间较短,可认为目标位置量测误差均方差和速度量测误差均方差基本不变,在不同既定毁伤概率m=4下,求得的射弹数m利用解析法与毁伤概率公式解得的概率为Pa和Pe如表3所示。 表3 预定毁伤概率情况下的射弹数 假设未来空域窗预定毁伤概率为Pc=0.55,设置未来空域窗瞄准点个数n=30,每个瞄准点配置弹丸数m=6,配置的未来空域窗[4]如图11所示。 通过统计模拟法对配置的未来空域窗毁伤概率进行仿真实验[5],其计算命中概率的基本步骤可归纳如下: 1)根据计算目的,确定概率模型; 2)确定初始数据; 3)确定各种随机变量的抽样方法; 4)依据模拟精度确定仿真次数; 5)开始仿真、判断命中; 6)计算总体的毁伤概率。 设定随机误差分布为正态分布,对随机误差抽样采用正态分布抽样。采用多门炮同时对瞄准点进行射击,统计模拟法置信概率α=95.4%,置信限ε=0.05,分别对统计模拟法进行100次蒙特卡洛仿真,得到其中20次未来空域窗射击体制下的毁伤概率Pa及集火射击体制下的毁伤概率Pc如表4所示。 表4 基于统计模拟法的全航路毁伤概率 通过分析仿真结果可得到以下结论: 1)基于统计模拟法得到的毁伤概率与理论毁伤概率存在部分偏差,其主要原因是因为在滤波算法中,目标的实际位置、速度与滤波得到的位置、速度均值及均方差值均存在偏差,因此在基于统计模拟法的仿真过程中,实际的毁伤概率相较于理论毁伤概率会偏低。 2)针对高超声速目标,当量测精度不高时,未来空域窗射击体制相较于集火射击体制,其对目标的毁伤概率更高,这与理论分析结果是一致的。 本文通过对未来空域窗全航路毁伤概率进行仿真分析,提出了利用未来空域窗拦截高超声速反舰导弹的主要流程,并针对未来空域窗全航路仿真的关键步骤,速度误差处理和命中判断问题进行了详细分析。最后依据未来空域窗全航路毁伤概率仿真计算流程,对未来空域窗和集火射击体制进行全航路毁伤概率仿真对比[6]。仿真实验表明,未来空域窗相较于集火射击毁伤概率更高,具有一定有效性和可行性,为下一步靶场实验奠定了基础。 [1] 卢发兴,贾正荣,吴玲,等.最优未来空域窗模型[J].系统工程与电子技术,2015,37(5):1073-1075. [2] 曾前腾,吴慧中.着发射击高射武器系统点射毁歼概率仿真[J].兵工学报,2006,27(1):126-131. [3] 刘恒,梅卫,单甘霖,等.基于蒙特卡罗法的高炮空域窗射击毁歼概率计算[J].火力与指挥控制,2014,39(1):87-91. [4] 卢发兴,贾正荣,吴玲,等.未来空域窗射弹丸瞄准点配置方法[J].兵工学报,2015,36(8):1541-1545. [5] 邢昌风,李敏勇,吴玲.舰载武器系统效能分析[M].北京:国防工业出版社,2007. [6] 胡炎,杨斌,苏卿,等.小口径舰炮武器系统射击方式比较[J].舰船电子工程,2010,30(6):24-27.3 仿真结果及分析
3.1 仿真条件
3.2 典型反舰导弹末端航路生成
3.3 目标跟踪及滤波

3.4 误差处理及最优射击时机选择
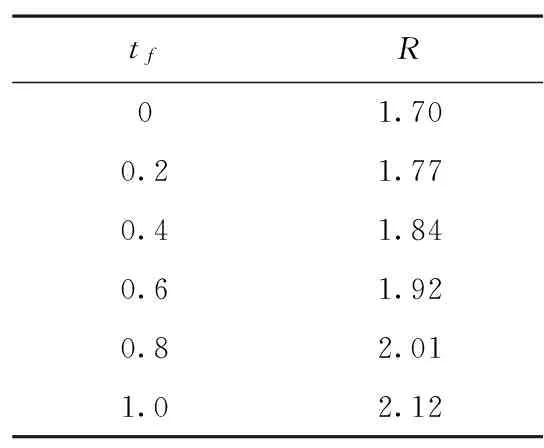
3.5 既定毁伤概率下的射弹数量求解
3.6 未来空域窗瞄准点配置
3.7 毁伤概率仿真

4 结束语
