导航信息处理中滤波算法稳定性评估方法

王 旺, 赵海军, 姜 暖

(海军潜艇学院, 山东 青岛 266042)

滤波算法在导航信息处理中有广泛应用,随着导航技术的不断进步,国内外学者提出了许多适合不同导航信息的滤波算法。稳定性是滤波算法得以正常工作的前提,是其性能的重要指标之一。评估滤波算法稳定性,有助于判断其优劣,以便为算法的使用和改进提供理论参考。目前,滤波算法稳定性评估主要是对其收敛性进行定性判断。文献[1]给出了滤波稳定性定理,即对于一致完全可控和一致完全可观测的系统,卡尔曼滤波算法是稳定的,但实际中往往会产生滤波发散现象。文献[1-3]提出了卡尔曼滤波过程的稳定性概念,给出了滤波发散的判定定理。文献[3]针对组合导航系统滤波算法,给出了性能指标和评估过程。文献[4-6]从定义出发研究了算法的稳定性,但未给出用于评估滤波算法稳定性的指标。

综合现有文献,有关滤波算法稳定性评估问题仅局限于稳定性概念及收敛判断条件,并没有给出评价稳定性的技术指标及精度要求,尚无完整的用于评价滤波算法稳定性的指标体系,本文在分析滤波算法稳定性影响因素的基础上,提出滤波算法稳定性评估指标,并给出了具体的数学表现形式,构建其指标体系,结合卡尔曼滤波在INS/GPS初始对准中的应用实例,对卡尔曼滤波的稳定性进行了评估,通过计算机仿真验证了所提指标的有效性。

1 滤波算法稳定性评估建模

稳定性是系统受到某一扰动后恢复原有运动状态的能力,即如果系统受到有界扰动,不论扰动引起的初始偏差有多大,在扰动撤出后,系统都能以足够的准确度恢复到原来的平衡状态,则称这种系统是稳定的[1]。

滤波算法的稳定性是其正常工作的前提,影响导航信息处理中滤波算法稳定性的主要方面有:收敛性、发散性、容错性及初值敏感性。

1.1 收敛性

收敛性是滤波稳定性评估最重要的方面,导航信息处理中滤波算法的目的是导航信息能够稳定收敛。

滤波收敛的判定为:若误差函数序列小于等于给定的发散检验阈值Δ,则称此次滤波收敛。

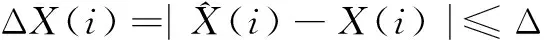
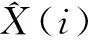
定义在N次滤波算法中,滤波收敛次数M与滤波总次数N的比值M/N为收敛度,记为ηa(0≤ηa≤1),即:

ηa=M/N

(1)

收敛度表征滤波算法收敛能力的强弱。其值越大,收敛能力越强;反之,越弱。收敛度与滤波算法的发散检验阈值Δ、滤波总次数N有关。

1.2 发散性

滤波发散的判定为:若误差函数序列大于给定的发散检验阈值Δ,则称此次滤波发散。

定义在N次滤波算法中,滤波发散次数L与滤波总次数N的比值L/N为发散度,记为ηb(0≤ηb≤1),即

ηb=L/N

(2)

发散度表征滤波算法发散能力的强弱。其值越大,越容易发散;反之,越不易发散。发散度也与滤波算法的发散检验阈值Δ、滤波总次数N有关。

根据上述定义,收敛度和发散度有如下关系:

ηa+ηb=1

(3)

1.3 容错性

当滤波算法的输入存在较大的波动或偏差(离群值)时,算法仍能满足一定导航精度要求的能力,称为容错能力或抗离群值能力。当离群值作为量测量进入滤波时,会对系统的滤波精度产生较大的影响,其影响可看作滤波算法的脉冲响应。描述滤波算法容错能力的指标主要有二次收敛时间和容错滤波精度。

当离群值作为量测量进入滤波算法时,会影响后续滤波算法的收敛,滤波算法在离群值出现后至再次稳定收敛所经历的时间,称为二次收敛时间t2。二次收敛时间是一时间区间,区间的大小反映了滤波算法在离群值存在的条件下再次稳定收敛的快慢。t2越大,滤波算法再次稳定收敛的速度越慢;反之,则越快。

t2=tw-tl

(4)

其中，tw为滤波值再次稳定收敛时刻;tl为离群值出现时刻。

容错滤波精度定义如下:

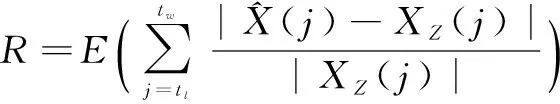
(5)

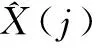
容错滤波精度为t2时间段内误差函数序列与相对真值比值的均值,反映了在离群值存在的条件下滤波值相对于相对真值的平均偏离程度,是一种相对精度。R值越大,滤波算法的抗离群值能力就越强;反之,则越弱。

1.4 初值敏感性

滤波算法的初值影响其精度及收敛时间。当滤波选取不同的初值,算法仍能稳定收敛至规定精度的能力,称为抗初值能力。其模型如下:

(6)

其中:ΔXw为稳态误差;Δ为发散检验阈值。

q值越大,滤波算法对初值越敏感;反之,则越不敏感。

1.5 滤波算法稳定性评估指标体系

基于上述分析,得到导航信息处理中滤波算法稳定性评估的指标体系，如图1所示。

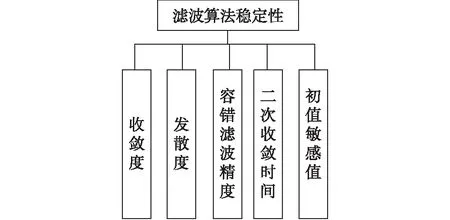
图1 滤波算法稳定性评估指标体系

2 仿真及结果

本文将卡尔曼滤波算法应用于INS/GPS组合导航系统初始对准中,并根据上述建立的滤波算法稳定性评估指标体系对卡尔曼滤波算法的稳定性进行评估。

2.1 动基座下初始对准动态方程的建立

在位置/速度组合模式中,将INS/GPS组合导航系统的误差量(位置、速度、平台误差角)作为滤波器的估计对象,动基座无阻尼惯导的误差方程[7]即可作为状态方程的一部分。为便于对惯性器件的误差源进行估计,陀螺漂移εx、εy、εz和加速度计误差ΔAx、ΔAy也应表示为系统的状态。假定3个陀螺漂移误差模型相同,均为一阶马尔科夫过程和白噪声之和,加速度计误差模型为零位偏置和白噪声之和,则滤波器状态方程如下:

(7)

式中,选取状态变量X=[δVx,δVx,δφ,φλ,φx,φy,φz,εx,εy,εz,ΔAx,ΔAy];F(t)为状态转移矩阵,由惯导误差方程[7]列出;w(t)为噪声向量,w(t)=[wAx,wAy,0,0,wgx,wgy,wgz,wmx,wmy,wmz,0,0]。wAx,wAy为加速度计误差的白噪声,wgx,wgy,wgz为陀螺漂移白噪声,wmx,wmy,wmz为激励白噪声。

令φt、λt为载体实际位置,vtX,vtY为载体实际速度,则惯导系统位置和速度可表示为

(8)

式中,φI、λI为惯导输出经纬度,vtIX、vtIY为惯导输出速度,δφ、δλ、δvX、δvY为惯导系统误差。

GPS位置和速度可表示为

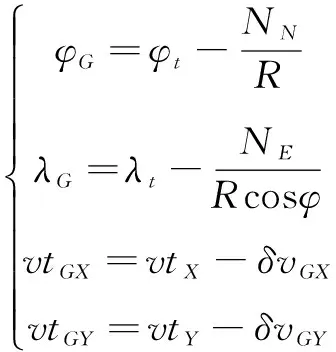
(9)

式中,φG、λG为GPS输出经纬度,vtGX、vtGY为GPS输出速度,δvGX、δvGY为GPS速度误差,NE、NN分别为GPS在经度方向和纬度方向的距离误差,为简便计,认为NE、NN为白噪声,R为地球半径。

在位置/速度组合模式中,定义量测向量:

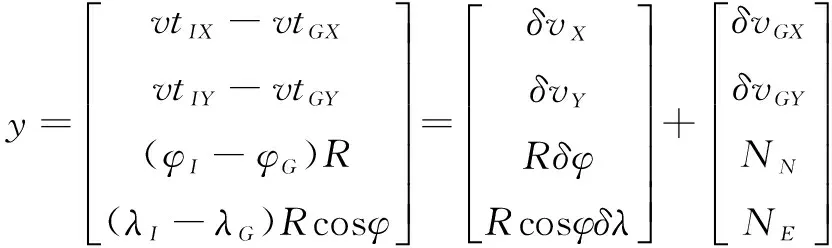
(10)

位置/速度组合模式下INS/GPS组合导航系统的量测方程为

Y(t)=H(t)X(t)+V(t)

(11)

式中,

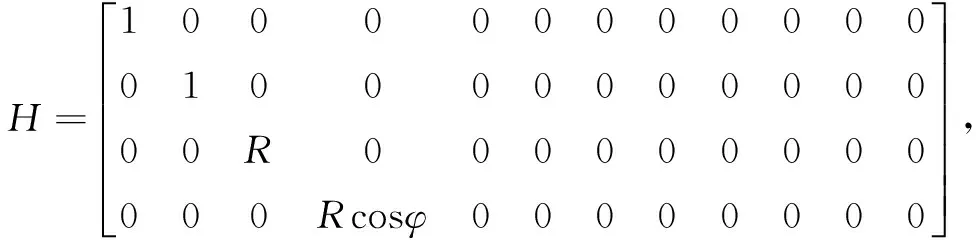
对于线性组合Z(t)=Lx(t),取

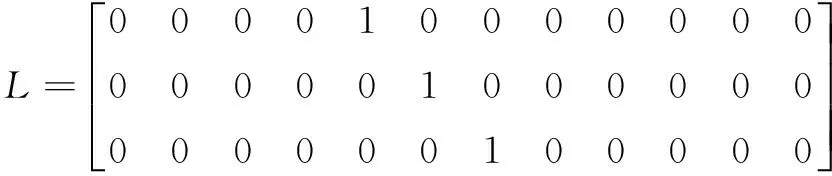
2.2 仿真条件

设载体为舰船,航速10kn,航迹如图2所示(横轴为经度,纵轴为纬度),包括正东向航行(航行时间20min)、圆周航行(航行时间10min)、正北向航行(航行时间15min)、西南向航行(航行时间40min)四个阶段。

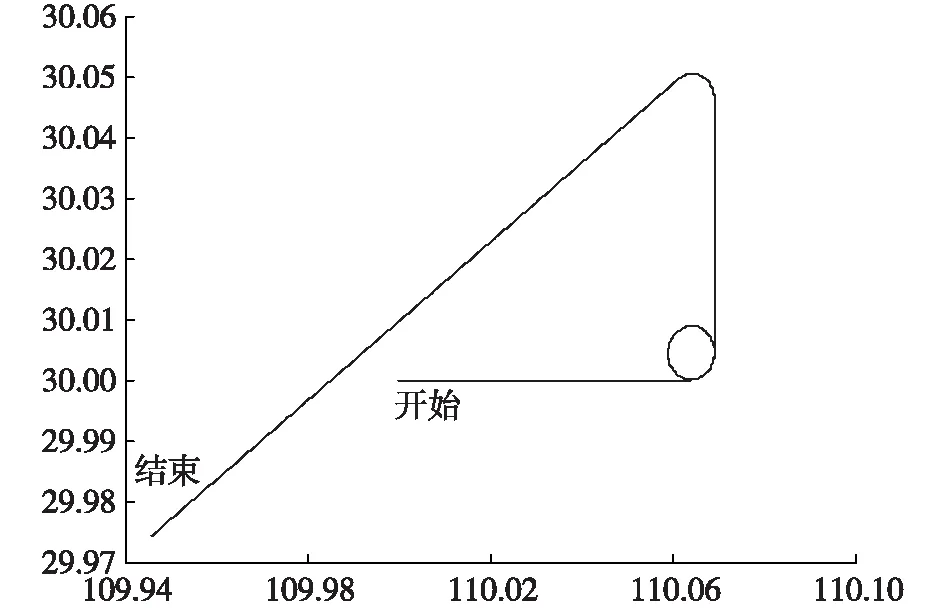
图2 仿真时的舰船“航迹”

取采样时间T=1s,地球自转角速率wie=7.29212e-5 rad/s,重力加速度g=9.78。假定选用一低精度惯导,其等效陀螺漂移为0.1°/h,随机漂移为0.001°/h,陀螺漂移相关时间为1h;加速度计零位偏置为10-4g,随机偏差为10-8;惯导平台的初始误差为φx0=5′、φy0=5′、φz0=20′,惯导初始定位误差北向和东向均为200m,初始速度误差为1m/s;GPS接收机输出的位置误差北向和东向均为25m,速度误差为0.1m/s。

2.3 卡尔曼滤波算法稳定性评估

条件1:

卡尔曼滤波算法的初值如下:

X0=[1m/s,1m/s,0,0,5′,5′,20′, 0.001°/h, 0.001°/h, 0.001°/h, 10-4g, 10-4g]

P0=diag{(1m/s)2,(1m/s)2,0,0,(5′)2,(5′)2,(20′)2,(0.001°/h)2,(0.001°/h)2,(0.001°/h)2,(10-4g)2,(10-4g)2}

Q0=diag{(10-8)2,(10-8)2,0,0,(10-8)2,(10-8)2,(10-8)2,(10-8)2, (10-8)2,(10-8)2,0,0}

R0=diag{(0.1m/s)2,(0.1m/s)2, (25m)2,

(25m)2}

状态初值X0和估计误差方差矩阵的初值P0为无偏的,即X0=E[X0]、P0=Var[X0]。发散检验阈值Δ1=Δ2=0.4′,Δ3=1.5′。稳定性评估指标数值如表1所示。误差估计结果如图3-5所示。

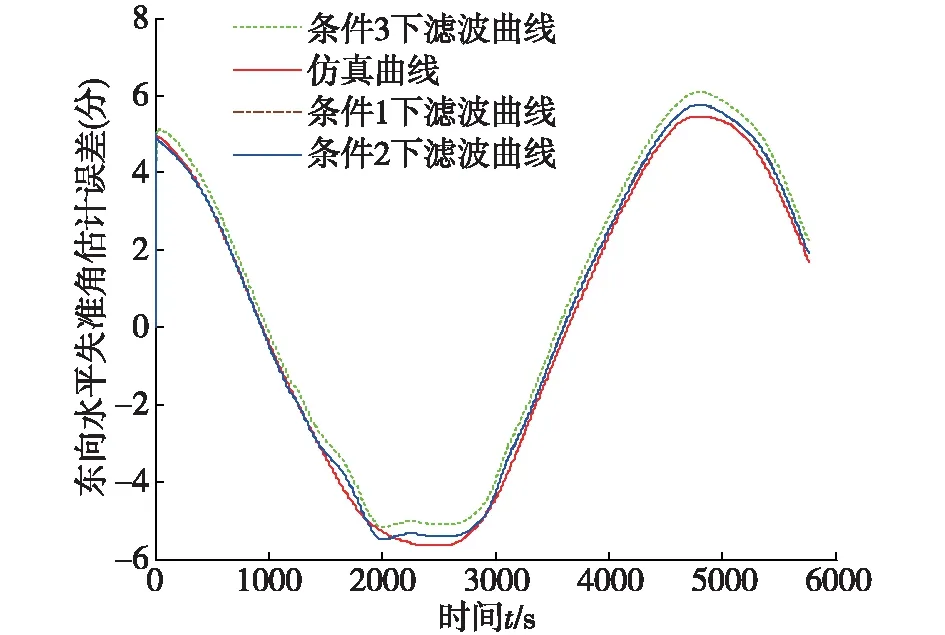
图3 东向水平失准角估计误差

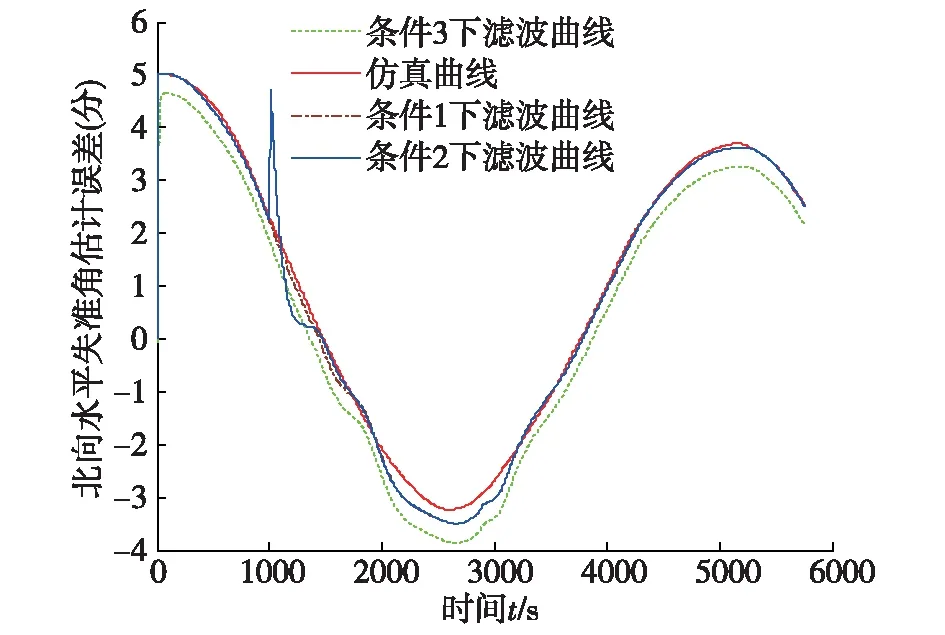
图4 北向水平失准角估计误差

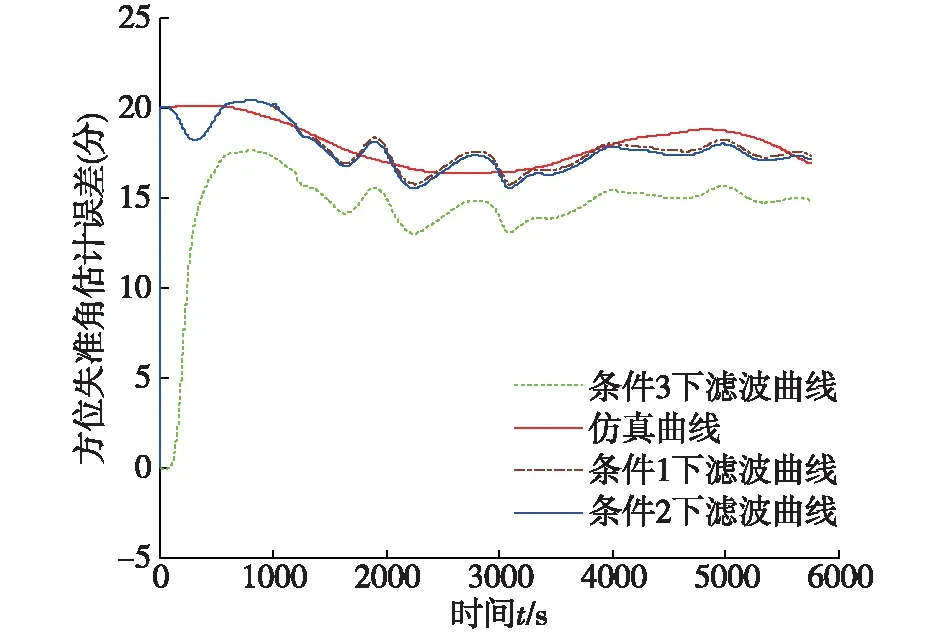
图5 方位失准角估计误差

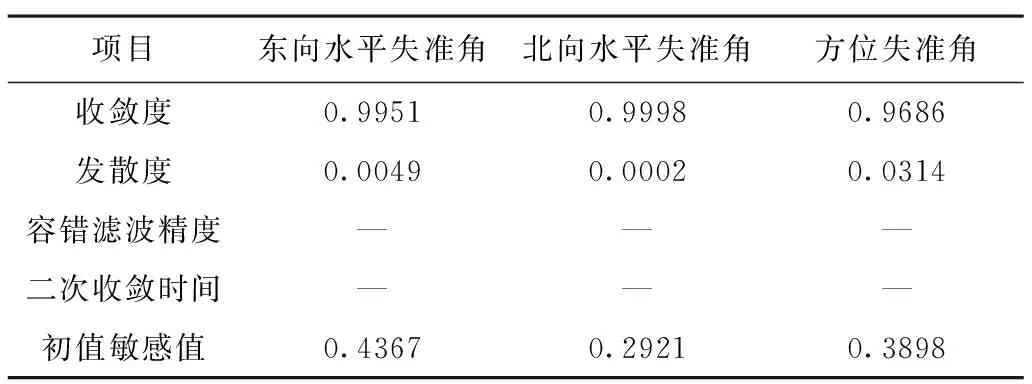
项目东向水平失准角北向水平失准角方位失准角收敛度0.99510.99980.9686发散度0.00490.00020.0314容错滤波精度———二次收敛时间———初值敏感值0.43670.29210.3898

条件2:

保持条件1的初值选取不变,引入离群值:惯导输出的东向速度在1000s:1010s=-8.0467m/s;发散检验阈值Δ1=Δ2=0.4′,Δ3=1.5′。条件2下的稳定性评估指标的数值如表2。

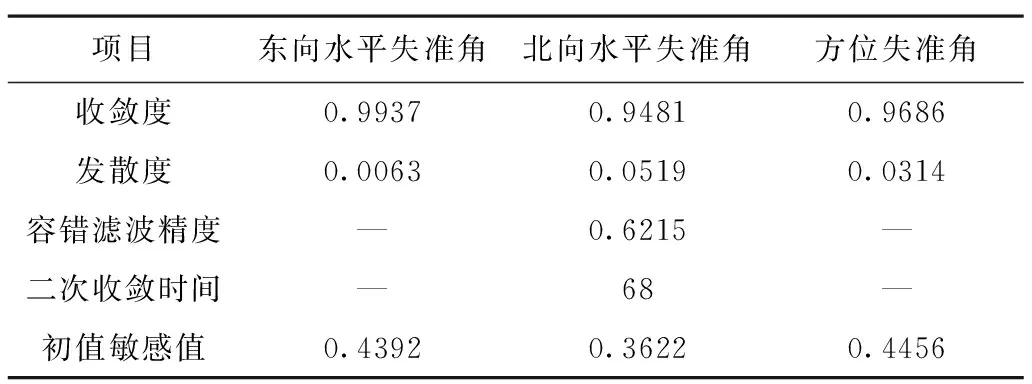
表2 条件2下的稳定性评估指标数值

条件3:

改变滤波算法的初值X0=[0,0,0,0,0,0,0, 0, 0, 0, 0,0];P0=diag{0,0,0,0,0,0,0, 0, 0, 0, 0,0};Q0和R0保持不变;发散检验阈值Δ1=Δ2=0.4′,Δ3=1.5′,此时不加入野值。评估数值如表3所示。

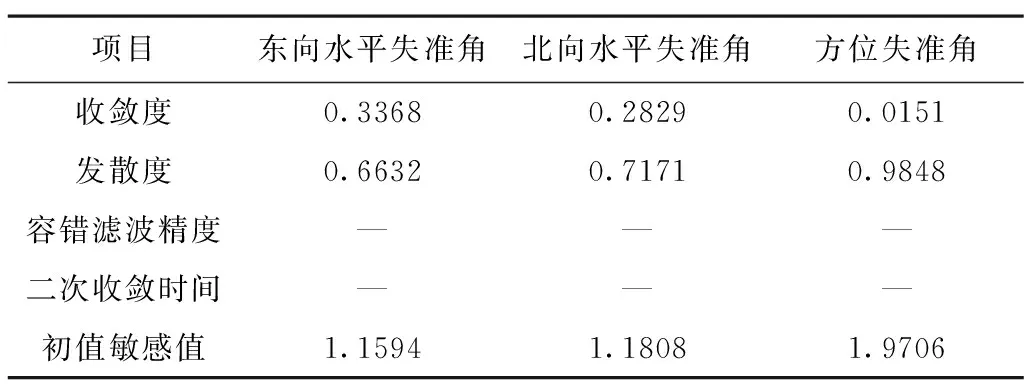
表3 条件3下的稳定性评估指标数值

由表1、表2,得出以下结论:在相同的发散检验阈值Δ1=Δ2=0.4′,Δ3=1.5′下,加入离群值后：

1)水平失准角的收敛度变小,方位失准角的收敛度没有变化;

2)与离群值相关的北向失准角的容错滤波精度为0.6215,即滤波值相对于相对真值平均偏离了62.15%。二次收敛时间为68s,再次稳定收敛的时间较长,说明了卡尔曼滤波算法的抗离群值能力较弱。

由表1、表3,得出以下结论:在相同的发散检验阈值Δ1=Δ2=0.4′,Δ3=1.5′下,改变滤波初值后：

1)三个失准角的收敛度均变小,且变化较大,可看出卡尔曼滤波算法的初值对滤波收敛及发散有较大影响;

2)由表3,三个失准角的初值敏感值均大于1,即稳态收敛误差大于发散检验阈值,说明卡尔曼滤波算法的初值影响其稳态收敛误差,抗初值能力较差。

综上,卡尔曼滤波算法在满足其假设条件下,稳定性好;但其抗离群值能力较差;当初值不满足无偏估计时,收敛性较差,抗初值能力较差。评估结果与理论分析一致。

3 结束语

稳定性是导航信息估计算法正常运行的前提和重要保障。本文以卡尔曼滤波在INS/GPS初始对准中的应用实例,得到了与理论分析一致的结论。但文中仿真条件只涉及了载体的航迹运动,载体舰船的姿态运动对滤波稳定性同样具有一定的影响,这也是需进一步分析的因素,有关这方面的内容将在后续工作中进一步深入研究。

[1] 邱恺,黄国荣,陈天如,等.卡尔曼滤波过程的稳定性研究[J]. 系统工程与电子技术，2005,27(1):33-35.

[2] K. You, M. Fu, L. Xie. Mean square stability for Kalman filtering with markovian packet losses[J]. Automatica， 2011,47(12):2647-2657.

[3] 邱恺,黄国荣,陈天如，等.基于滤波过程的卡尔曼滤波发散判定方法[J].系统工程与电子技术， 2005,27(2):230-231.

[4] 刘勇志,贾兴亮,刘丙杰.一种组合导航滤波性能评估算法[J].弹箭与制导学报，2008,28(5):45-47，50.

[5] 刘国良,张迎春,孙增圻.联邦滤波器的滤波稳定性研究[J].中国惯性技术学报，2004,12(6):28-31.

[6] 高法钦,谈展中.北斗组合动态定位算法稳定性分析[J].电子与信息学报，2007,29(10):2388-2391.

[7] 陈永冰,钟斌.惯性导航原理[M].北京:国防工业出版社,2007.

[8] 阎红星,王晓博,王国宏.跟踪滤波算法性能评估研究[J].现代雷达，2008,30(4):33-36.

[9] Boyi Ni, Qinghua Zhang. Stability of the Kalman Filter for Output Error Systems[J]. IFAC,2015，48(28):1106-1111.

[10] A li T A, John E G, Mc Cabe D H. Performance Evalunation of a Asynchronous Multisensor Track Fusion Filter[C]∥Proceedings of SPIE,2003.

[11] Junfeng Wua, Ling Shi b, Lihua Xie.An improved stability condition for Kalman filtering with bounded Markovian packet losses[J]. Automatica, 2015,62(C):32-38.