基于DS-GRA机载雷达组网资源管理效能评估

2018-03-19杨文平

指挥控制与仿真 2018年1期

杨文平

(西安爱生技术集团公司, 陕西西安 710065)

机载雷达作为空战中的“电子眼”,相对地基雷达可以利用高度优势更早对来袭目标进行预警,尽早争夺制空权、获取空中优势[1]。机载雷达组网系统资源管理是指利用多个雷达获取关于目标和环境的信息,通过网内信息共享,恰当地分配或驱动网内各雷达及雷达载体协同完成相应的任务,以使任务性能最优。同时,在一定约束条件下,根据某种最优准则确定各雷达的最佳工作方式及参数[2]。目前,关于雷达资源管理方面的研究主要集中在对相控阵雷达的资源管理上,包括相控阵雷达能量管理、采样间隔管理、组网雷达任务调度和分配等方面[3],而且主要针对地基雷达,而对于机载雷达这种空基组网资源管理效能评估研究较少。

本文根据机载雷达组网资源管理研究的现状,结合目前复杂电子战环境下所要求的抗自卫干扰(Self-Screening Jamming,SSJ)基本任务,比较全面地给出了机载雷达组网抗SSJ干扰的资源管理效能评估指标体系,提出了采用DS证据理论[4](Dempster-Shafer Evidence Theory)与灰色关联分析[5](Grey Relational Analysis,GRA)相结合的综合评估方法。该方法避免了传统层次分析法(Analytical Hierarchy Process,AHP)需要对所有指标进行“两两比较”标度,判断矩阵元素标度之间具有耦合性,必须对判断矩阵一致性进行检验等不足。

通过具体的实例计算,验证了该方法的可行性,并且通过评估对机载雷达组网资源管理决策的优化提供了依据。

1 机载雷达组网抗SSJ干扰资源管理效能评估指标体系

机载雷达资源管理的范围主要包括:时间资源管理、空间资源管理、能量资源管理、轨迹资源管理等。根据这些资源管理的范围,遵循全面性、层次性、客观性、准确性等原则,同时兼顾高动态环境下雷达组网链路传输的约束,建立机载雷达组网抗SSJ干扰资源管理评估指标体系如图1所示。

1)雷达自卫距离[6]：当信干比满足一定条件下接收机最小可检测强度时,对目标的探测距离称为雷达的自卫距离。反映在信干比一定时雷达组网的探测能力。

2)抗干扰成功率：在系统的运行过程中,我方雷达网络使用资源管理系统抗干扰的成功率。当雷达自卫距离>径向距离时表示抗干扰成功;反之,则抗干扰失败。

3)雷达补盲成功率：在系统运行过程中,我方雷达受到干扰时,其他雷达进行补盲的成功率。

4)链路传输速率：一定时间内系统通过战术数据链传输的数据量,其值为接收数据的总比特数与接收时间的比值。

2 基于DS-GRA的综合评估方法

本文提出的DS-GRA综合评估方法,由多个专家分别对单个指标独立打分,根据专家个人权重的不同修正初始信度矩阵,得到指标的基本信度分配矩阵,然后利用Dempster证据合成法则对多位专家的基本信度矩阵进行融合,得到综合评估信度,然后再根据评价值公式,计算出该指标的评价值。同理,可以得到所有指标的评价值,最后根据各指标的评价值算出各自的权重向量。最终,把由DS证据理论方法确定的指标权重与灰关联分析得到的灰关联系数矩阵乘积加权求和,得到机载雷达组网抗SSJ干扰资源管理效能评估结果。

2.1 资源管理评估指标权重向量的计算步骤

步骤1:专家打分等级的建立

将各因素对于整个系统的重要性的等级进行划分,并且用 [0,1]之间的数值进行表示,将分数的等级分为5级,见表1所示。

表1 打分等级表

步骤2:基本信度矩阵的计算[7]

决策者或专家通过对各因素在系统中重要性的客观分析,给出基本可信度分配的定量值,构建指标重要性初始信度矩阵。

若ejk是非关键指标,其基本概率赋值为

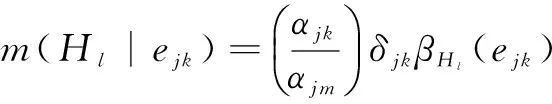
(1)

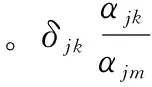
步骤3:指标评价值的计算

对于子系统因素中假设包含有因素集I(n)={ei1,ei2,…,ein},则用证据理论结合准则产生的综合集函数记为

(2)

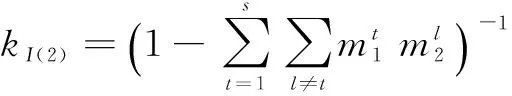
(3)

l=1,2,…,z

(4)

根据Dempster证据合成法则,按照以上综合集函数的求取对多位专家打分基本信度矩阵进行融合,得到融合后信度分布如表2所示。

表2 融合后ejk信度矩阵

结合表1中分数值为系数,获得指标ejk重要性评价值为

(5)

同理,按照以上步骤计算出所有指标的评价值。

步骤4:各指标权重向量的计算

指标ejk的权重为

(6)

其中,l为指标ejk所在层所有指标个数的总和。据此,可以计算出所有指标的权重向量。

2.2 灰关联系数矩阵的建立

灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近,相应序列之间关联度就越大,反之就越小[9]。

设X0=(x0(1),x0(2),…,x0(n))为系统特征序列(参考序列),且

X1=(x1(1),x1(2),…,x1(n))
…
Xi=(xi(1),xi(2),…,xi(n))
…
Xm=(xm(1),xm(2),…,xm(n))

为相关因素序列。

其中基于灰关联公理与灰关联差异信息空间LYgr,并考虑其“领域性”与规范区间性,则灰关联系数的算式为[10]

(7)

在本文中,将相关因素序列的灰关联系数γ(x0(k),xi(k))构成m×n阶矩阵,则称

(8)

为灰关联系数矩阵。

2.3 基于DS-GRA方法的资源管理综合评估结果的确定

结合多专家权重向量,以及灰关联系数矩阵,即可以得到机载雷达组网系统抗SSJ干扰资源管理性能的综合评估结果,其计算公式如下:

Q=wΦ=(q1,q2,…,qm)T

(9)

其中,Φ=(γij)m×n是灰关联系数矩阵,w=(w1,w2,…,wn)T是多专家权重向量,同样n代表指标个数,最后求得的Q值即是机载雷达组网资源管理的综合评估值,其值越大,表明采取的组网技术效果越好。

综合以上评估步骤,给出DS-GRA综合评估方法的流程,如图2所示。

3 仿真实例

以某型战机机载雷达组网为例,假定高动态战场环境尺寸为250km×250km×100km,敌我双方相距300km,在空中相向而行,我方根据对方SSJ干扰状态,实施抗SSJ干扰,如图3所示。

根据抗SSJ干扰所涉及的资源管理技术,对空间、时间、能量、链路等资源的原始指标值进行归一化处理,计算出各指标值如表3所示。

表3 抗SSJ干扰指标归一化值

3.1 传统AHP方法的评估仿真

1)根据各指标对抗SSJ干扰资源管理的影响大小,对两两指标分别进行比较得到方案层各因素之间的判断矩阵,如表4所示。

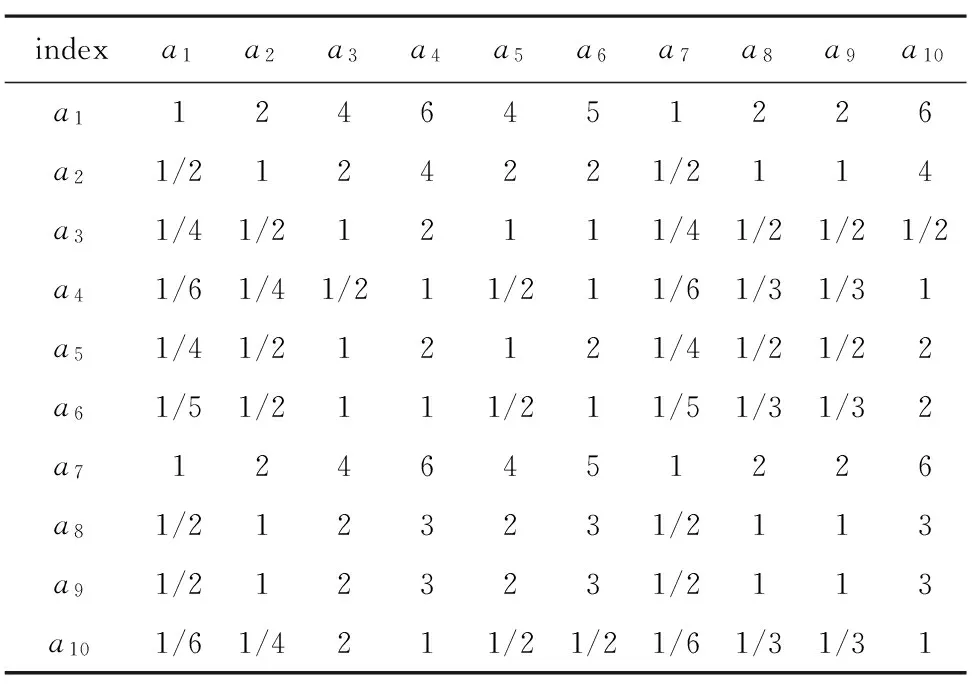
表4 抗SSJ干扰专家判断矩阵

2) 一致性检验。采用萨迪教授提出的比例一致性检验方法,得出判断矩阵的一致性比率值为:CR=0.0162,一致性比率值小于0.1,可知判断矩阵具有广义的一致性。

按照数理统计中的假设检验,得到导出矩阵为:

C=[1.0157 1.0232 0.9445 0.9527 1.0525 0.9797 1.0157 1.0232 1.0232 0.9694 0.9725 0.9797 0.9043 1.2162 1.0077 0.7504 0.9725 0.9797 0.9797 1.2375 1.0720 1.0799 0.9968 1.3406 1.1108 0.8272 1.0720 1.0799 1.0799 0.3410 1.0759 0.8129 0.7504 1.0091 0.8361 1.2453 1.0759 1.0838 1.0838 1.0268 0.9046 0.9113 0.8412 1.1313 0.9373 1.3960 0.9046 0.9113 0.9113 1.1511 0.9916 1.2486 1.1526 0.7750 0.6422 0.9564 0.9916 0.8324 0.8324 1.5772 1.0157 1.0232 0.9445 0.9527 1.0525 0.9797 1.0157 1.0232 1.0232 0.9694 0.9962 1.0036 0.9264 0.9344 1.0323 1.1531 0.9962 1.0036 1.0036 0.9508 0.9962 1.0036 0.9264 0.9344 1.0323 1.1531 0.9962 1.0036 1.0036 0.9508 0.9252 0.6991 2.5811 0.8678 0.7190 0.5354 0.9252 0.9321 0.9321 0.8830]

3)在权重向量的计算中采用“特征值法”,按照公式Aw=λmaxw,w是相应的特征向量,所得到的w经归一化后就可作为权重向量,如图4所示。

4)评估结果为:组网0.7803,单机0.3437,如图5所示。

单独采用传统的AHP方法,能够对机载雷达组网抗SSJ干扰资源管理效能评估,但通过其评估过程可以发现该方法有以下不足:

①对所有指标要进行“两两比较”,当指标因素过多(超过9个)时,标度工作量太大,易引起标度专家反感和判断混乱。

②判断矩阵的元素标度之间具有耦合性,某一标度的改变会对其他元素造成影响,甚至产生矛盾冲突。

③对于判断矩阵,必须进行一致性检验,检验过程复杂。并且随着判断矩阵阶数的递增,通过检验的成功率大大降低。

3.2 基于DS-GRA方法的评估仿真

鉴于传统AHP方法的不足,本文提出了DS-GRA综合评估方法,以下采用该方法对机载雷达组网抗SSJ干扰资源管理进行效能评估仿真。

1)指标初始信度矩阵

专家组根据自身的经验、知识和对该指标所做的观察和研究分析,给出指标e11的打分结果,如表5所示。

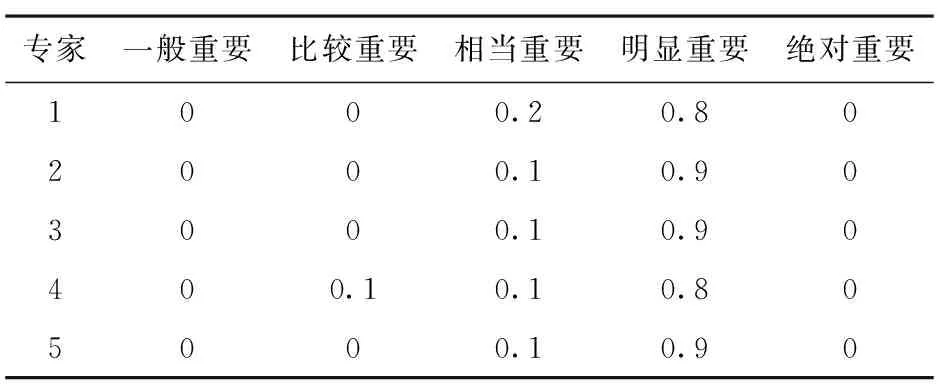
表5 e11重要性初始信度矩阵

2)基本信度矩阵的确定

设5位专家的权重为{α1,α2,α3,α4,α5}={0.2,0.15,0.25,0.1,0.3},δjk=0.9。求出各位专家的可靠度,对初始信度矩阵进行修正,得到指标e11的基本信度矩阵如表6所示。

表6 e11重要性基本信度矩阵

3)基本信度的融合

根据Dempster多个信度函数的合成规则,对5位专家的基本信度矩阵进行融合,得指标e11的合成可信度为:m(Hi|e11)={0,0.0002,0.0150,0.9791,0}。

4)计算e11重要性评价值

m(H|e11)=0×0.1+0.0002×0.3+0.0150×0.5+0.9791×0.7+0×0.9=0.6929

同理可得其他指标的重要性评价值。

以下为三组专家对各个指标独立打分后,运用DS证据理论获得机载雷达组网“抗SSJ干扰”指标重要性评价值,如表7所示。

表7 方案层指标的评价值

5)各指标权重向量的计算

利用权重计算公式(6),得到方案层指标的三组权重(如图6)为:

W1=[0.1105 0.0933 0.0527 0.1397 0.0521 0.0461 0.1070 0.0875 0.1527 0.1585]T。

W2=[0.1093 0.0900 0.0674 0.1500 0.0556 0.0382 0.1075 0.0842 0.1392 0.1587]T。

W3=[0.1102 0.0928 0.0555 0.1423 0.0485 0.0438 0.1063 0.0979 0.1469 0.1558]T。

6)灰关联系数矩阵的计算

7)综合评估结果的计算

最终,应用公式(9)计算得到机载雷达组网抗SSJ干扰资源管理效能评估综合结果(如图7)为:

组网Q=wΦ=[0.8249 0.8194 0.8247]

单机Q=wΦ=[0.3437 0.3438 0.3436]。

通过以上三组结果对比分析得:①机载雷达组网的效能评估结果远远大于单部雷达的评估结果,充分体现了现代战争中网络中心战的优势。②本文提出的DS-GRA方法对于单部雷达的评估结果0.3437、0.3438、0.3436与AHP方法的评估结果0.3437基本一致,而对于组网雷达的三组评估结果0.8249、0.8194、0.8247均优于传统AHP方法的评估结果0.7803。按照文献[12]给出的模糊评语集,即“差”、“较差”、“一般”、“良”、“优”,记对应模糊评价值为:p(H)={p(H1),p(H2),p(H3),p(H4),p(H5)}p(H5)}={0.2,0.4,0.6,0.8,1},DS-GRA方法对于机载雷达组网资源管理抗SSJ干扰效能评估结果均处于“良”和“优”之间,而传统AHP方法评估结果处于“一般”和“良”之间。③对于该机载雷达组网系统,三组不同的专家通过独立打分,运用DS-GRA方法获得评估结果基本一致,而传统AHP方法的评估结果与多位专家的评估结果差别较大。④对比指标权重,“链路传输正确码率”和“链路传输速率”两个指标所占权重比例较高,说明在高动态环境下,机载雷达组网链路传输的约束对整个效能评估具有关键性影响。

4 结束语

目前,传统AHP方法,DS证据理论,灰色关联分析这些近代理论各自单独作为一种评估方法已经被应用到系统工程中。本文在此基础上,综合考虑DS证据理论、灰色关联分析各自的优势,将DS证据理论与灰色关联分析法(GRA)相结合,提出了DS-GRA综合评估方法。该方法相比传统AHP方法具有以下优势,如表8所示。

最后以机载雷达组网抗SSJ干扰资源管理效能评估为例,验证了DS-GRA方法相比传统AHP方法对于多指标、多专家评估时的优势,该方法为机载雷达组网资源管理效能评估提供一种可行的技术途径,评估结果为机载雷达组网资源管理的进一步优化提供了参考依据。

表8 DS-GRA与传统AHP方法的比较

[1] 白尊辉.机载雷达组网探测航迹融合优化处理技术研究[D].成都:电子科技大学,2016.

[2] 贲德,韦传安等.机载雷达技术[M].北京:电子工业出版社,2006.

[3] Xiao-JieGu,Xin-Min Wang,Kai-Rui Zhao,Yan Li. Autonomous Resource Management System of Netted Radar for Tactical Aircrafts. Proceedings of the 2009 IEEE International Conference on Control and Automation, Christchurch, NewZealand, December 9-11, 2009.

[4] G Shafer. A Mathematical Theory of Evidence[M]. Princeton University Press,Princeton,1976.

[5] 雷明剑,于淼.基于灰色关联分析法的巡航导弹发射阵地选择[J].指挥控制与仿真,2016,38(4):36-38.

[6] 陈永光,李修和,沈阳.组网雷达作战能力分析与评估[M].北京:国防工业出版社,2006.

[7] 韩德强,杨艺,韩崇昭.DS证据理论研究进展及相关问题探讨[J].控制与决策,2014,29(1):1-7.

[8] 何小雨,杨璐萍,吴韬，等.群层次分析法和证据推理法在绿色建筑评价中的应用[J].系统工程,2016,34(2):77-80.

[9] Chin-Tsai Lin, Shiuh-Nan Hwang, Chia-Ho Chan. Grey number for AHP model-an application of grey relational analysis. Proceedings of the 2004 IEEE International Conference on Networking, Sensing & Control Taipei, Taiwan, March 21-23, 2004.

[10] 陈晓坤,蔡灿凡.不同因素对煤岩导热系数影响的实验研究[J].煤矿安全,2017,48(3): 18-21.

[11] 程晓娟,韩庆兰,全春光.基于灰关联分析的GA-BP神经网络在汽车油耗估算中的应用[J].数学的实践与认识,2016,46(8): 43-47.

[12] 张幸,胡建旺,郝永峰.基于改进模糊综合评判法的C3I系统效能评估[J].电光与控制,2011,18(4):41-45.