基于数学形态学的雷达图像边缘检测算法

易成涛, 徐 飞

(海军大连舰艇学院, 辽宁 大连 116018)

长期以来,图像边缘都是反映图像本身特征信息最好的载体,人们一直致力于边缘检测技术的研究与发展,但是由于受到图像本身较为复杂，噪声和目标边缘在检测中均为有效边缘，匹配中使用的边缘信息各不相同等因素影响,使得边缘检测技术至今仍为一个难题[1-2]。因此目前边缘检测方面还是以针对具体课题使用具体方法,针对具体研究改进检测算法为发展方向。

目前边缘检测技术主要有经典边缘检测技术,如: Sobel算子、Roberts算子、Prewitt算子等;线性滤波边缘检测技术,如:Log算子、Canny算子等,还有尺度空间滤波理论、小波变换、模糊集合论、神经网络等新型边缘检测技术。

数学形态学是通过集合方式来处理图像的一种非线性方法和理论,近年来成为图像边缘检测中的一个新的研究领域。利用该方法进行图像处理具有简化图像数据、保持图像基本结构特征、除去不相关结构、运算简单等优点,在噪声去除、边缘检测、特征提取等图像处理领域都有广泛的应用。

1 数学形态学

数学形态学的中心思想是将图像看作点的集合,然后采用结构元素对其进行移、交、并的集合运算。因此结构元素在数学形态学中占据十分重要的地位,它实际上也是一种点的集合,不同点集合构成的结构元素具有不同的特性,一般使用圆形、正方形、十字形、菱形等结构元素,结构元素在目标图像中进行移动就是数学形态学的基本处理方法。

由于本文获取的雷达图像是二值化处理后的图像,并且二值形态学处理较为简单,硬件实现更加高速,因此本文采用数学形态学中二值形态学。

2 数学形态学基本运算

2.1 膨胀和腐蚀

膨胀和腐蚀是数学形态学运算中最基本的变换[3]。关于膨胀和腐蚀的定义如下[4]:

A⨁B={x|∃a∈A,∃b∈B:x=a+b}

(1)

AΘB={∃a∈A,∀b∈B:x=a-b}

(2)

式中⨁和Θ为集合的Minkowski和与差变换符,(A)b是集合A关于集合B的平移集合,(A)-b是集合A关于集合B映像的平移集合。由此设定A为输入二值图像矩阵,B为结构元素矩阵。

2.2 开运算和闭运算

膨胀和腐蚀运算不互为逆运算,因此将它们进行结合使用可以构造不同的运算方式。对输入图像先进行腐蚀运算再进行膨胀运算称为开运算(开启运算),对输入图像先进行膨胀运算再进行腐蚀运算称为闭运算(闭合运算)[5]。

定义开运算和闭运算的公式如下:

A∘B=(AΘB)⨁B

(3)

A·B=(A⨁B)ΘB

(4)

其中∘和·分别为开运算和闭运算的运算符号。

3 改进数学形态学滤波方法

传统的数学形态学滤波的具体方法如下:设输入雷达图像为A,选取的结构元素为B,首先利用结构元素B对雷达图像A进行膨胀运算,然后再用B进行腐蚀运算,这种方式可以将目标特征附近的孤立点等噪声去除;然后利用B对其进行腐蚀运算,再进行膨胀运算,这样可以将雷达图像内部的噪声去除。从上述步骤中可以看出前两步运算的实质是数学形态学中的闭运算,后两步为开运算。设C为滤波处理后得到的图像,定义公式如下[6]:

C1={[(A⨁B)ΘB]ΘB}⨁B=(A·B)∘B

(5)

多次实验证明上述传统的数学形态学滤波方法对于雷达图像的滤波不是很理想,根据上述公式可以延伸出一种类似的滤波处理公式[7]:

C2={[(AΘB)⨁B]⨁B}ΘB=(A∘B)·B

(6)

由此,将上述两个公式进行组合,可以得出一种新型的滤波处理方法,数学形态学公式如下:

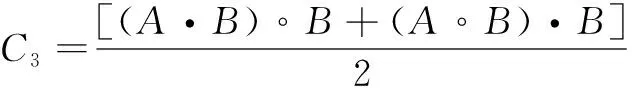
(7)

4 改进的数学形态学边缘检测算法

根据数学形态学的基本运算方法,可以推算出图像的边缘检测算法,令Y为图像边缘,A为输入图像,B为结构元素[8]。首先让输入图像A经过结构元素B腐蚀,然后求得输入图像A与腐蚀图像之差即为边缘图像Y,称为内边界边缘检测器,推算公式如下:

Y=A-(AΘB)

(8)

同理,首先让输入图像A经过结构元素B膨胀,然后求得膨胀图像与输入图像A之差即为边缘图像Y,称为外边界边缘检测器,推算公式如下:

Y=(A⨁B)-A

(9)

结构元素的选取是数学形态学边缘检测算法的一个关键,不同结构元素的选取会导致运算过程中对图像不同几何形状的分析和处理,同时结构元素的不同使用也决定了计算精度的不同,因此对结构元素的分析选取使用是数学形态学边缘检测算法的重要内容。

上述介绍了几种改进型边缘检测算法,虽然能够很好地在抑制噪声和保持细节方面达到平衡,但是致命缺点是只采用了一种结构元素,不能很好地感知图像的不同几何形状。而数学形态学的灵活多变形式注定它要采用不同的结构元素来提高边缘检测的效果[9-11]。因此本文将上述公式进一步改进,既能够充分保留目标图像的细节,又能够很好地抑制噪声,提取更加理性的目标图像边缘。改进公式依次如下:

Y=[(AΘB1)⨁B2]⨁B3-[(AΘB1)⨁B2]·B

(10)

其中B1、B2和B3为选取的不同结构元素。

5 改进算法实验性能比较

本文以494×494像素的实装雷达图像作为输入图像进行综合性能评估,所有方法的试验平台与运行环境为Microsoft Windows 7,Intle(R)Core(TM)i5-6200U CPU@2.30GHz 2.30GHz,Matlab R2013a。

图1为实装雷达图像,图2和图3分别给出了雷达图像预处理过程中的灰度图像和二值图像,方便后续的边缘检测算法性能比较。

改进型数学形态学滤波方法的过程图如图4所示:首先利用结构元素B对雷达图像A进行闭运算操作,再对其进行开运算;然后利用结构元素B对雷达图像A进行开运算操作,再进行闭运算。最后将这步骤中的结果进行平均运算,得出最终的雷达滤波图像结果如图5所示。相比较原始的二值图像,经过滤波处理后的雷达图像更加平滑,大多数特征信息更加清晰,噪声等干扰在一定程度上能够得以抑制,对于提高边缘检测算法的精准度具有一定的帮助作用。

图6和图7分别给出了雷达图像在Sobel算子、Roberts算子、Prewitt算子、Log算子、Canny算子以及本文提出算法上的边缘检测结果。

使实装雷达图像叠加均值为0,方差为0.01的高斯白噪声,将其作为输入图像进行综合性能评估,图8和图9分别给出了与前面相对应的各种算子和本文算法的边缘检测结果。

由表1可知,在时间上本文提出的算法只比其他边缘检测算法多大约0.2s,但是由图7对实装雷达图像和图9对叠加高斯白噪声的实装雷达图像的边缘检测结果可以看出:

在雷达图像没有加入高斯白噪声的时候,基于梯度的边缘检测算法都能够很好地检测出雷达图像的边缘,但是当加入高斯白噪声以后,Log算子和Canny算子受到的影响较大,基本不能实现雷达图像正常的边缘检测,其他算子受到的影响较小。没有噪声加入时,Log算子检测出的目标边缘容易产生伪边缘,这与其检测的理论有关,无法得到根本性的转变。

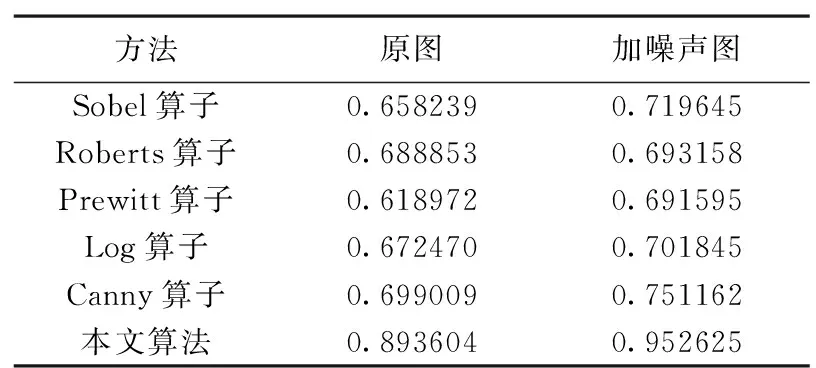
表1 边缘检测算法结果图

基于梯度的边缘检测算法,模板简单,操作易于实现,但是这种方法存在着边缘定位不准确,检测得出的雷达图像边缘并非单像素,同时抵抗噪声的能力较差。

6 结束语

本文采取的基于改进型数学形态学的边缘检测算法具有更好的细节处理和抗噪声性能,它能够很好地得到单像素的图像边缘。且应用于雷达图像的边缘提取中效果更加显著,能够提取出更加完整的图像特征信息,为雷达图像的后续应用提供了良好的基础。

[1] 章毓晋.图像工程(中册)——图像分析[M].第2版.北京:清华大学出版社,2005.

[2] 章毓晋. 图像处理和分析[M].北京:清华大学出版社,1999.

[3] 朱庆华,常莹. 基于数学形态学预处理的Canny边缘检测算法[J]. 中国市场,2016(49):85-86.

[4] 陈茹,张珍明,邢益雪,等. 一种改进的含噪图像边缘检测算法[J/OL]. 无线电工程,2016,46(6):38-40.

[5] Gonzalez R C,Woods R E.Digital image processing(2nd Edition)[M].Beijing:Publishing House of Electronics Industry,2003:420-510.

[6] 凌永国,韦树贡. 基于边缘和数学形态学复杂背景车辆定位[J]. 广西民族师范学院学报,2017,34(3):131-133.

[7] Maragos P.Differential morphology and image processing[J].IEEE Trans Image Processing,1996,5(6):922-937.

[8] 徐国雄,张骁,胡进贤,等. 基于阈值分割和轮廓提取的图像边缘检测算法[J/OL]. 计算机技术与发展,2015,25(12):64-67+71.

[9] 朱地博,李春贵,张延丽. 抗噪形态学图像边缘检测算法的研究[J]. 信息技术,2017,41(7):115-117.

[10] Chen T,Wu Q H,Torkaman R R,et al.A pseudo top—hat math-ematical morphological approach to edge detection in dark regions[J].Pattern Recognition,2002,35(11):199-210.

[11] Aci’on S T,Mukherjee D P.Area operators for edge detection[J].Pattern Recognition Letters,2000,21(8):771-777.