基于Kuramoto的常规导弹作战体系同步效能评估*

林伟廷, 曹 娟

(1.国防科技大学信息通信学院, 湖北 武汉 430010;2.火箭军指挥学院, 湖北 武汉 430017)

常规导弹作战体系构成要素多,各要素间信息交互关系复杂,是典型的复杂巨系统,其作战体系效能的发挥很大程度上依赖于作战体系的同步能力。影响常规导弹作战体系同步能力的因素较多,本文重点关注指挥信息流程这个关键因素对作战体系同步效能的影响。

1 常规导弹作战体系同步过程分析

1.1 作战体系的抽象

常规导弹作战体系内包含大量侦察情报单元、指挥控制单元和火力打击单元等实体,如果将各类实体抽象为具有动力学特性的节点V1,V2,…Vi,那么各实体之间的信息交互关系,则可以抽象为节点V1,V2,…Vi之间的连接边E11,E12,…Eij。基于上述抽象过程,常规导弹作战体系则可以看作是由大量周期性变化振子按照一定拓扑结构组成的动力学系统。

1.2 同步效能评估维度

常规导弹作战体系的同步效能受到认知、信息和行动等多个方面的影响,覆盖战役战术等不同层面,因此对常规导弹作战体系同步效能进行评估时,难以建立综合全面的指标体系覆盖所有因素。为了简化建模的难度,参照相关研究成果的思路[1-2],选取时间作为主要特征参数,从时间维度重点考察作战体系内不同指挥信息流程对作战体系同步效能的影响。

1.3 常规导弹作战体系同步过程的抽象

本文将常规导弹作战体系同步抽象为多周期振子耦合的复杂系统同步问题,利用经典的Kuramoto同步模型对常规导弹作战体系的同步过程进行定量描述,进而分析指挥信息流程模式对作战体系同步效能影响,如图1所示。首先,利用OODA模型描述作战体系内各节点的指挥活动过程,将其区分为“观察、判断、决策、行动”四种基本状态。其次,假设作战体系内各个节点按照各自独立的频率四种状态间不断循环,各节点通过指挥信息交互,调整各自周期实现整体同步。

2 基于Kuramoto的常规导弹作战体系同步模型

在对常规导弹作战同步过程进行抽象的基础上,进一步提出建模的假设条件,并基于Kuramoto相振子模型构建常规导弹作战体系同步模型。

2.1 Kuramoto相振子模型

Kuramoto相振子模型利用相位方程对有限个振子组成的网络动态特性进行描述,非常适合研究系统的同步问题。由于模型清晰简单,易于理解,在电力、军事、社会等领域的复杂系统同步行为建模研究中得到广泛应用。

N维Kuramoto模型的数学描述为

(1)

式中,θi表示振子节点Vi的相位,ωi表示振子节点Vi的固有频率,K表示耦合强度。当两个振子之间没有耦合作用(K=0)时,每个振子以自然频率运动,当引入耦合后,振子之间会出现相同步,振子之间保持稳定的相位差[3]。

对于振子网络的同步能力利用参序量r(t)进行衡量。参序量r(t)定义为

(2)

式中,φ(t)表示振子集合的相位平均值;θj表示网络中节点Vj的相位;参序量r(t)描述网络内振子动力学行为的一致性,用来衡量网络整体同步程度,r(t)∈(0,1)。当r(t)→0时,表示整个网络处于完全无序状态,当r(t)→1时,表示网络实现整体同步。

2.2 基本假设条件

假设条件一:将常规导弹作战体系内主要节点区分为情报单元、火力单元和指控单元三类。情报单元包括无人机、侦察卫星、预警机等各类战场侦察系统等;火力单元主要包括火力发射单元;指挥单元是具有作战指挥职能的实体,如常规导弹旅等指挥机构。

假设条件二:将常规导弹作战体系内各单元抽象为具有时间周期的节点,各节点按照各自的频率进行着“侦察、判断、决策、行动”的OODA循环。其中,节点处在作战体系内的层级越高,其OODA周期越长;反之,其OODA周期较短。

假设条件三:节点之间的连接则表示作战单元之间的信息交互关系,其连接强度由节点之间的信息交互频率和信息量决定。信息交互越频繁,连接强度越大,反之则越小。

2.3 常规导弹作战体系同步模型

基于上述的假设条件,在对常规导弹作战体系进行适度抽象和简化的基础上,构建常规导弹作战体系同步模型如下。

(3)

式中,θi表示各节点Vi所处的OODA阶段,θi∈[0,2π],按照固定频率ωi匀速变化。将0～2π均分为4个象限,以相位所处象限表示节点Vi的OODA阶段。当θi∈[0,π/2)时,表示节点Vi处于侦察情报获取阶段;当θi∈[π/2,π)时,表示节点Vi处于信息分析处理阶段;当θi∈[π,3π/2)时,表示节点Vi处于决策计划阶段;当θi∈[3π/2,2π)时,表示节点Vi处于执行任务阶段,如图2所示。

ωi表示节点Vi的固有频率,与节点Vi的OODA周期成反比。ωi与节点Vi所处作战体系的层级,作战指挥环境,以及节点自身信息处理效率等因素相关。通常,位于指挥体系底层的节点,如常规导弹旅指挥所,完成OODA的循环速度较快,则ωi较大;而位于作战体系高层的节点,例如高层的常规导弹作战指挥机构,完成一次OODA循环较慢,则ωi较小。

aij表示节点Vi和节点Vj之间的信息交互关系。当aij=0时,表示节点Vi和节点Vj之间不存在信息交互关系,当aij=1时,表示节点Vi和节点Vj之间存在信息交互关系。

kij表示节点Vi和节点Vj之间的信息耦合强度。在作战体系同步的过程中,各节点之间通过信息交互,不断调整自身频率ωi,也就是加快或减慢相应节点信息处理的速度。耦合强度kij通常受节点之间信息交互数量、交互频率以及信息相关度等因素影响。kij越大,表示交互强度大;kij越小,表示交互强度弱。

N表示作战体系内节点的数量。

3 同步能力度量指标

为了有效评估不同指挥信息流程控制模式对作战体系同步能力的影响,论文将同步能力评估指标r(t)定义为

(4)

式中,φ(t)表示作战体系内所有节点的相位平均值;θj(t)表示网络中节点Vj处于OODA的具体阶段;参序量r(t)描述作战体系内各节点的整体同步程度,r(t)∈(0,1),当r(t)→0时,表示整个作战体系状态处于无序状态,当r(t)→1时,表示作战体系实现了整体同步。

3.1 编组内同步能力判据

对于编组内信息流程模式的同步能力,主要采用参序量r(t)和同步时间Tsyn两个参数综合进行衡量。

r(t)表示同一编组内节点之间的同步程度,r(t)∈[0,1];当r(t)的数值越接近1时,表示各个节点状态一致性越好,反之,r(t)越小,说明各节点所处OODA的一致性就越差。r(t)=1表示作战体系内所有节点之间保持完全同步的状态。对于由N个节点组成的编组,参序量r(t)计算方法如下。

(5)

r(t)具有三种取值的可能:一是保持固定的数值;二是在一定范围内保持波动;三是呈现发散状态。判断作战体系是否达到同步可采取以下方法。

对于参序量r(t),当t>tε时,如果能够找到一个足够小的常数ε,对于任意Δt>0,均满足|r(t+Δt)-r(t)|≤ε,则认为节点组成的编组实现了状态同步。式中能够满足要求的最小时间Tsyn,是编组的同步稳定时间。

3.2 编组内同步能力评估指标

当编组实现稳定同步时,编组的同步能力计算方法如下。

Ms=rs·βTsyn

(6)

式中,Ms表示编组的同步能力,rs是系统稳定后的参序量均值,Tsyn表示体系实现同步稳定的时间,β∈[0,1]表示调节因子。

4 仿真与结果分析

根据常规导弹作战指挥的特点,选取三种典型的指挥信息流程控制模式,进行仿真实验和数值分析,比较不同指挥信息流程控制模式对于整个常规导弹作战体系同步能力的影响。

4.1 仿真实例

本文重点考虑常规导弹作战情报保障关系和指挥层级两个因素,构建三种典型的指挥信息流程控制模式,研究相关因素对常规导弹作战体系同步效能的影响。

第一种称之为“三层指挥体制+独立情报保障”指挥信息流程控制模式。在该模式中,常规导弹作战采取三层指挥体制,侦察情报信息直接提供给最高层联合作战指挥机构,联合作战指挥机构逐级指挥导弹旅作战,其指挥信息流程拓扑结构如图3所示。

第二种称之为“两层指挥体制+独立情报保障”指挥信息流程控制模式。在该模式中,常规导弹作战指挥体制由三层压缩为两层,侦察情报信息仍然由外部情报源直接传递给最高指挥机构,其指挥信息流程拓扑结构如图4所示。

第三种称之为“两层情报保障+分散情报保障”指挥信息流程控制模式。在该模式中,常规导弹作战采取扁平化的两层指挥体制,外部情报机构将情报信息同时推送给最高指挥机构和导弹旅,缩短侦察情报信息在整个作战体系内的流通路径,实现侦察情报信息在末端直接交联,其指挥信息流程拓扑结构如图5所示。

4.2 参数设置

本文基于Kuramoto的作战体系同步模型进行仿真实验,目的是为了得到趋势性的结论,因此,在保持合理比例的情况下,可以适当控制模型中节点数量,减少仿真计算量。在仿真过程中,假设常规导弹作战指挥机构直接指挥4个常规导弹旅,每个导弹旅直接指挥3个发射架;侦察情报体系的指控单元下辖3个侦察情报源,节点总数控制在23～25的规模。

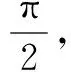
4.3 仿真计算结果

本文在Matlab7.0环境下对采取三种典型指挥信息流程模式时,常规导弹作战体系的同步效能进行仿真评估,得到参序量r(t)变化曲线图,如图6、图7、图8所示。

采取三种指挥信息流程控制模式时,常规导弹作战体系的同步能力参数具体如表1所示。

表1 采取三种信息流程模式时系统同步能力

4.4 实验结果分析

比较表1实验结果,发现采用模式三“两层指挥体制+分散情报保障”指挥信息流程模式时作战体系同步效能最好,采用模式二“两层指挥体制+独立情报保障”指挥信息流程模式时作战体系同步效能次之,采用模式一“三层指挥体制+独立情报保障”时作战体系同步效能最差。在模式一中,不同的编组都能够最终保持同步,但是参序量r(t)呈现周期性震荡,作战体系的同步效果不理想。这是由于指挥信息链路过长,不同层级节点间OODA周期相差较大,无法形成完全同步的行动。在模式二中,各个编组的参序量r(t)趋于固定的数值,这是由于两层的指挥体系,使得不同指挥层级间节点的OODA周期差距变小,在同一编组内的各节点能够保持较为稳定状态差。模式三相比模式二,各个编组的参序量r(t)均有所提高,同步时间得到缩短。这是由于侦察情报信息直接推送至常规导弹旅,打通了侦察情报节点和火力打击节点之间信息交互通道,使得整个作战体系的同步效能得到进一步的增强。

根据上述分析,提高常规导弹作战体系的同步效能,可以重点从以下几个方面着手。一是构建扁平化的指挥体系,减少不同层级之间的OODA周期差距;二是依托信息网络增强作战体系内各节点之间的信息交互强度;三是构建多维协同关系,提高作战体系内各节点之间的联通密度。

5 结束语

本文分析了影响常规导弹作战体系同步效能的相关因素,重点研究指挥信息流程对作战体系同步效能的影响。在对常规导弹作战体系同步过程进行抽象的基础上,建立基于Kuramoto的常规导弹作战体系同步模型,提出作战体系同步的相关判据。将常规导弹作战体系的信息流程模式归纳为“两层指挥体制+分散情报保障”、“ 两层指挥体制+独立情报保障“、”三层指挥体制+独立情报保障”三种类型,并通过仿真比较了三种指挥信息流程模式对作战体系同步效能的影响。最后,结合常规导弹作战体系特点,从指挥体制、信息网络和协同关系等三个方面给出提高常规导弹作战体系同步效能的相关建议。

[1] 李启元.网络化指挥控制系统同步特性分析[J].海军工程大学学报,2014，26(5)：48-52.

[2] 王欣等.基于任务的网络中心战作战同步能力度量[J]. 火力与指挥控制,2013，38(1)：96-101.

[3] 汤亚锋,于小红.空间信息支援力量编组模式分析[J].指挥控制与仿真,2015，37(6)：12-17.

[4] 王树国.几类复杂动力网络的同步分析与控制研究[D].江苏大学,2013.

[5] 李福涛,马静,邹艳丽.几种Kuramoto振子网络同步性能的比较[J].广西师范大学学报,2011，29(4)：16-20.

[6] 邹志刚,刘付显,夏璐.从时间角度看作战决策同步[J].电光与控制,2013，20(3)：25-29.

[7] 赵明,周涛,陈关荣.复杂网络上动力系统同步的研究进展[J].物理学进展,2008(1)：22-34.

[8] 王斌.基于复杂网络的作战同步建模研究[D].长沙:国防科学技术大学,2007.

[9] Anthony H. Dekker. Analyzing C2 Structures and Self-Synchronization with Simple Computational Models[C]. Quebec City, Canada:16the ICCRTS,2011.

[10] Alexander Kalloniatis, Mathew Zuparic. The J-Staff System, Network Synchronisation and Noise[C]. Alexandria, VA:19th ICCRTS, 2014.