高地应力钻孔岩心饼裂特征研究

，，，，

(1.长江科学院 水利部岩土力学与工程重点实验室，武汉 430010；2.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

1 研究背景

岩心饼化是钻探取心过程中特有的岩石力学现象，现有研究成果表明，高应力环境下钻孔岩心的饼化现象发生与否是宏观判断钻孔所在部位岩体应力是否属高应力或极高应力的主要判断依据。

早在20世纪60年代，国外已有学者对钻孔岩心饼化现象进行了相关研究，其中关于饼裂机制主要有2种观点：沿岩饼破裂面的剪切破坏和沿钻孔方向的拉张破坏。Obert和Stephenson(1965)[1]对大理岩进行了室内三轴应力状态的钻孔试验，观察到岩饼端面存在与三轴剪切破坏裂痕一致的痕迹；Durelli等(1968)[2]通过光弹试验证实了钻孔过程中岩心底部边缘存在剪应力集中，并指出当剪应力大于抗剪强度即发生岩心饼化的岩心饼裂条件；Jaeger和Cook(1963)[3]基于对岩饼断面形貌的细观研究，最早指出饼化机理为受拉破坏，这一观点在后续的许多试验研究及理论分析工作中得到了相应的支撑。Dyke(1989)[4]、Li和Schmitt(1997)[5]、Matsuki等(2004)[6]、Kaga等(2003)[7]通过三维数值模型分析了钻心过程中岩心中拉应力的变化，建立了相应张拉破坏准则。Corthésy(2008)等[8]使用弹塑性软化模型对钻孔岩心进行了数值模拟，指出岩心饼裂机制有张拉破坏、剪切破坏及张拉剪切联合破坏3种，不同的应力场及岩体张拉剪切强度比，破坏机制不同。

国内学者自20世纪80年代以来，围绕二滩正长岩、天荒坪河床凝灰岩、三峡茅坪深孔花岗岩等工程高应力钻探岩心饼化问题，在高应力条件下钻孔岩心饼化特征、岩体结构与应力条件对岩心饼化的影响以及岩心饼化过程断裂机制分析等方面也取得了重要进展[9-12]。目前的研究表明，地应力大小不是决定岩心饼化的唯一因素，应力方向、岩体结构强度、钻孔速率、孔径同样对岩心饼裂的破坏机制及几何形态有着一定的影响[13]。

随着经济建设与国防建设的不断发展，深部岩体工程越来越多,深部岩体工程在开挖洞室或巷道时，围岩变形和破坏等出现了一系列新的科学现象,如岩爆、围岩挤压大变形以及围岩的分区破裂化现象[14]。钻孔勘探作为了解深埋岩体特性的第一窗口，不仅是岩体取样和岩体结构编录的主要手段，同时深部岩体钻孔取样和深埋隧洞开挖类似，钻孔过程中岩心所产生的饼化等现象也反应了岩体-应力释放的相互作用。因此，研究高应力钻孔过程中岩心的饼化特征，可以了解应力场、应力释放对岩体的影响，对高应力地区地应力大小及隧洞开挖过程中岩爆等动力地质灾害进行预测和评估。

本文总结分析已有的研究成果，对锦屏深部岩体典型钻孔岩心饼化特征开展了调查统计分析，在对岩饼形貌以及钻孔过程岩心饼裂现象的描述基础上，结合数值模拟方法对钻孔岩心饼裂进行了机理分析。研究成果对高应力条件下的地应力场的预测、钻孔取心等工作具有一定的借鉴意义。

2 锦屏深部岩体典型岩饼形貌特征

本文利用锦屏白山组 T2b大理部分地应力测试钻孔进行岩心饼裂特征分析，其中：75 mm直径岩心为锦屏地下实验室二期7#实验室洞壁钻孔岩心；48 mm直径岩心为2#试验支洞(长江科学院深部岩体力学特性试验场地)底板钻孔所取。部分岩心如图1所示，共统计Φ75 mm岩心240 m，Φ48 mm岩心100 m。

图1 锦屏深部大理岩(T2b)岩心Fig.1 Core of marble rock (T2b) in Jinping deep underground

图2 鞍形岩饼起伏形态与主应力关系Fig.2 Relationship between principal stress and topogra-phy of saddle core disk

2.1 岩饼端面形貌特征

岩饼端面形貌与饼裂机制及地应力场关系密切，岩饼表面断口是否存在剪切擦痕或拉坎也成为研究者宏观上判断饼裂机制是否为剪切或拉断的主要依据。

对于均质完整性较好的岩石，岩饼端面起伏主要呈平整形、凹面形、鞍形等，其中凹面及鞍面的凹曲方向始终与钻孔方向一致。在实际钻孔过程中，受钻头振动、水压、岩石节理以及岩石自身矿物不均匀性的影响，岩心饼裂的形态及端面的起伏会更加多样。在几种岩饼端面形态中，以鞍形最为特殊，Haimson等[15]通过钻孔试验证实了鞍形岩饼的凹轴与岩心径向平面内的最大主应力方向一致，如图2所示。

本文所统计的部分Φ75 mm和Φ48 mmT2b大理岩钻孔岩心中，岩饼端面以鞍形为主，平面形次之，部分岩饼受自身节理及洞室开挖影响残缺不全。岩饼端面主要特征为：岩饼端面新鲜，无浸染痕迹；岩饼破裂面上在平行于凸轴的方向上沿凹轴逐级分布拉张断裂坎，拉张断裂坎呈梯级分布且与凸轴具有一定的对称性，如图3所示。

图3 岩饼端面形貌Fig.3 Texture of core disk surface

2.2 岩饼侧面形貌特征

岩饼的侧面形貌主要体现在岩饼的厚度以及裂纹的分布上。厚度主要受地应力大小和岩石强度控制，对于同类岩石，当场地地应力较大时，钻进较小深度即可在岩心根部产生较大的拉应力及剪应力，因而岩饼厚度越薄；而当地应力场一定时，岩石强度越高，就需要钻进更大的深度使岩心根部产生超过岩石破裂强度的应力，形成的岩饼相对较厚[16]。

对所选钻孔进行岩饼厚度统计分析，其中Φ75 mm岩心中岩饼的厚度集中在15～25 mm范围内，Φ48 mm岩心中岩饼厚度集中分布在5～15 mm，岩饼厚度随钻孔直径增大而增长。图4为岩饼厚度H与直径D比值(厚径比H/D)的统计分布。从统计结果可知：2种直径岩饼厚度分布范围不同，但其厚径比的期望值同在0.2～0.3范围内，仅略有差异。

图4 岩饼厚径比统计分布Fig.4 Statistics of core disk thickness-diameter ratio

与之类似的统计结果也在其他研究中出现，如:姚宝魁[9]对二滩坝址Φ56，Φ110，Φ130 mm 3种直径的正长岩钻孔进行了饼化现象统计，3类钻孔中，岩饼的平均厚径比分别为0.265，0.27，0.27；刘世煌[10]对拉西瓦电站Φ56 mm钻孔直径的花岗岩进行了岩心饼化统计，岩饼的平均厚径比为0.26；李占海等[17]对锦屏深部实验室钻孔岩饼厚度进行了统计分析，其结果为：当孔径为Φ75 mm时，岩饼厚度集中在1.54～1.97 cm，当孔径为Φ91 mm时,岩饼厚度集中在1.86～2.38 cm，2种直径岩饼换算之后的厚径比均在同一范围内。

3 钻孔岩心应力特征分析

在钻孔切割过程中，岩心内部应力状态十分复杂，基于本文所观察的岩饼断口以拉裂断坎为主，通过建立二维有限元弹性模型来分析钻孔过程中岩心内部拉应力变化，对钻孔岩心饼化现象及岩饼特征进行力学揭示。

使用ABAQUS软件进行数值模拟，参数参考文献[18]中锦屏T2b大理岩力学试验结果，取弹性模量E=64 GPa，泊松比μ=0.26，单位采用国际标准单位系统，拉应力为正、压应力为负，所建立的几何模型如图5所示。其中:D为岩心直径；h为钻孔深度；d为切缝宽度。

图5 钻孔岩心二维几何模型Fig.5 Two-dimensional geometric model of rock drilling

3.1 钻孔岩心拉应力特征

在模型中预加岩心轴向应力场(Sv)和岩心径向应力场(Sh)来模拟地应力场，通过分步单元移除来模拟钻孔切割过程。图6为模型轴向应力场Sv=40 MPa，径向应力场Sh=80 MPa，岩心直径D=0.06 m时，不同钻孔深度的岩心中最大主应力(σ1>0时)云图及矢量图。由图6可见：当钻孔切割使岩心失去侧向约束，原本处于受压状态的岩心在根部出现拉应力；岩心内部最大拉应力方向与岩心轴向接近平行，夹角在0°～10°范围内；岩心内拉应力区呈凹曲条带状，凹曲方向与钻孔方向一致，拉应力区的形状与鞍形岩饼的端面凹曲形状相似；随着钻孔深入，岩心内部拉应力区分布趋于稳定变化。

图6 不同钻孔深度的岩心拉应力云图及矢量图Fig.6 Contours and vectors of tensile stress in rock core at different drilling depths

3.2 裂纹初生与扩展

岩心内部的拉应力随钻孔深入而增大，直到处于稳定变化阶段，钻进过程中，当岩心某部位拉应力大于岩石的抗拉强度时，即会发生局部开裂进而扩展贯穿至整个岩心形成岩饼。

图7 钻孔岩心最大拉应力分布Fig.7 Distribution of maximum tensile stress in drill core

从最大拉应力的数值大小以及在钻孔过程中出现的位置来看，岩心中初始裂纹出现在III区的概率更大，对应的裂纹扩展模式为：首先岩心表面局部出现拉裂纹，而后裂纹扩展至贯通岩心表面，同时裂纹向岩心中心扩展直至岩心完全饼裂。在所调查的钻孔岩心中，还存在半饼化的岩心，岩心表面局部形成饼裂纹，正是裂纹在表面扩展阶段。

3.3 岩心饼裂与地应力场的关系

地应力越大，相应的岩饼厚度越小，除了通过实测数据拟合岩饼厚度与地应力大小的关系式外，国内外许多学者也基于各种饼裂破坏理论，通过数值、解析、模型试验等方法推导出以岩饼几何参数来估算地应力大小的数学公式。本文将选取拉应力参数，基于岩心张拉破坏的饼裂机制，通过二维弹性有限元分析，来分析地应力大小与岩心饼化的关系。

3.3.1 张拉破坏指标

前文在对钻孔过程模拟中，当钻孔到某一深度时，岩心内部拉应力区将贯通，将拉应力区中各径向坐标的最大拉应力连接起来，可得到最大拉应力贯通线，如图8所示。定义最大拉应力贯通线上最小拉应力为贯通拉应力，记为σtc，其含义是岩心内部能形成贯穿岩心的拉应力云图的最大值，从图8中可直观理解其含义，当拉应力云图的下限>σtc时，岩心内部拉应力云图会断开[6]。

图8 最大拉应力贯通线和贯通拉应力Fig.8 Line of maximum tensile stress and penetrative tensile stresses

当钻孔岩心以张拉破坏形式饼化时，在钻孔过程中，岩石抗拉强度σT、最大拉应力σtmax以及贯通拉应力σtc会存在以下几种关系：①σT>σtmax时，岩心内部不会出现张拉裂痕；②σT<σtc时，岩心内部存在大于岩石抗拉强度的贯通拉应力带，岩心会张拉饼裂；③σtc<σT<σtmax时，岩心内部会出现局部张拉裂纹，可能不完全饼裂。

前2种关系可以明确判断岩心是否发生张拉饼裂，当使用σT<σtc为判据研究饼裂与地应力的关系时会高估地应力大小，相应地，使用σT<σtmax又会低估地应力的大小。而实际上应力大小并不是决定饼裂的唯一因素，基于断裂力学分析,当σtc<σT<σtmax时，也可能发生岩心完全饼裂。本文在以下的分析中，引入岩心中最大拉应力贯通线的均值σta，图9为Sv=40 MPa,Sh=80 MPa,D=0.06 m时，岩心中σtmax,σta,σtc随钻孔深度的变化。σta介于σtmax与σtc之间，呈指数曲线形态，相比σtmax,σtc的变化特征,σta可以更好地进行拟合分析，因此本文将以σT<σta作为张拉饼裂的判据。

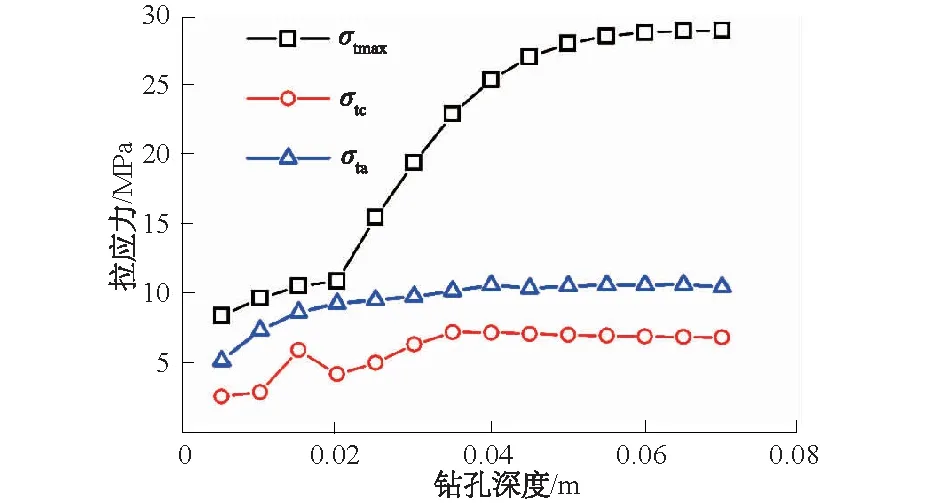
图9 最大拉应力、贯通拉应力及贯通线均值应力随钻孔深度的变化曲线Fig.9 Curves of maximum tensile stress, penetrative tensile stress and average value of maximum tensile stress cross line versus drilling depth

3.3.2 岩心直径与岩饼厚度

虽然双胞山药因为藤蔓短可以不搭架，但经我们研究，搭一个0.6 m左右高的矮架更有利于通风透光和田间管理，具有明显的增产作用。也可采取插桩的办法，用长度为70 cm左右的粗芦苇或桑条等，一穴插一根桩。

通过对锦屏深部实验室岩饼的统计可知，小直径钻孔中岩心饼化的比率更高。本文通过分析不同直径岩心钻孔的应力状态来进行揭示。

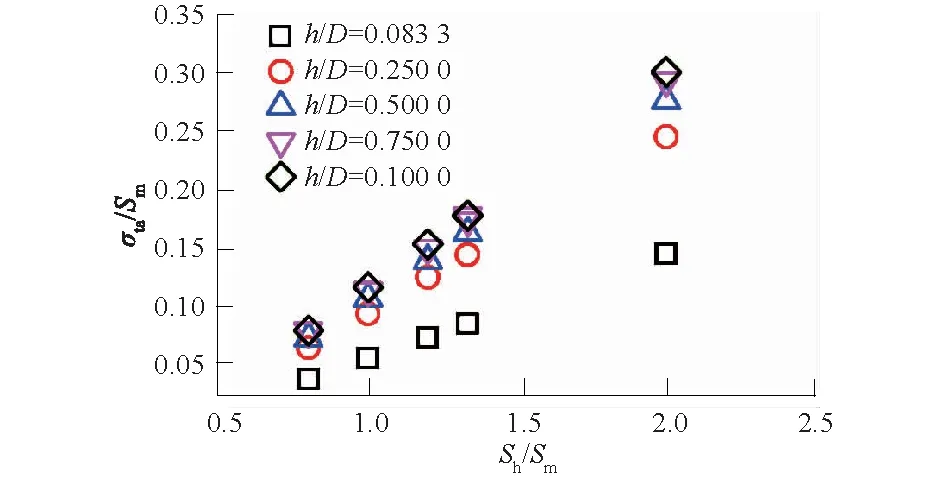
图10为岩心直径D=0.04，0.06，0.08，0.10 m，应力场Sv=40 MPa,Sh=80 MPa时，最大拉应力均值σta随钻孔深度的变化，钻孔深度用深度与岩心直径的比值(h/D)表示。图10中显示:σta随钻孔深入而增加，不同直径钻孔的σta-h/D曲线形态基本一致;在00.6之后，σta趋于稳定；钻孔直径越小，σta最终越大。因此对于同一应力场和岩性，小直径钻孔中能达到的破坏拉应力更大，相应的小直径钻孔中岩饼出现的概率更高。

图10 不同直径岩心最大拉应力贯通线均值随钻孔深度的变化曲线Fig.10 Average value of maximum tensile stress cross line in rock core of different diametres against drilling depth

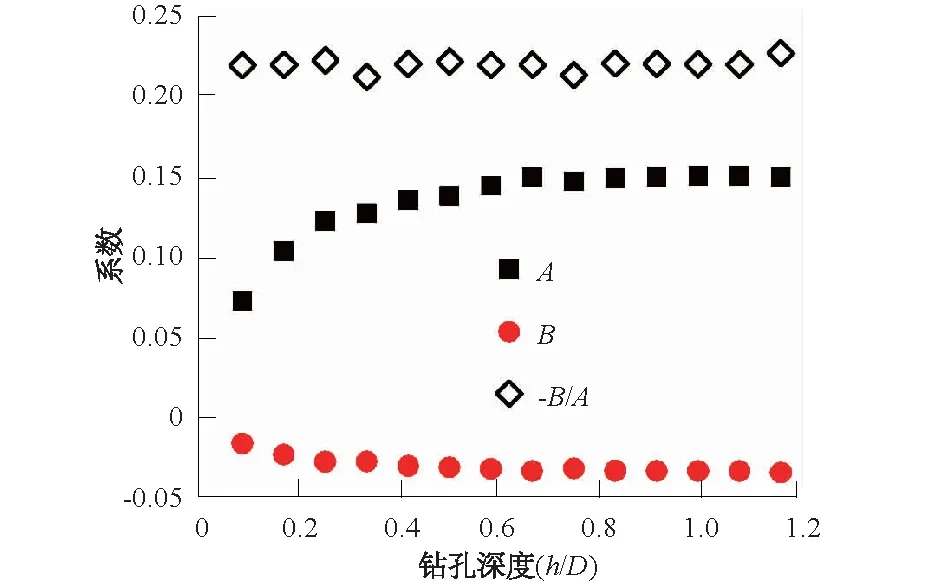
对于不同直径的钻孔岩心，当0

3.3.3 Sh与Sv对饼化的影响

已有研究表明当钻孔轴向应力场增大时，就需要更大的径向应力场才能使岩心饼裂[1]。本文对D=0.06 m的钻孔数值模型施加不同的轴向应力场和径向应力场组合，计算最大拉应力均值，来分析钻孔轴向应力场Sv和径向应力场Sh对岩心饼化的影响。如图11所示，当Sv=40 MPa时，各钻孔深度的最大拉应力均值随Sh增大而增大；相反，当Sh=40 MPa时,各钻孔深度的最大拉应力均值随Sv增大而减小。该关系表明，对于岩心钻孔，Sh增长有利于岩心饼化，而Sv增长不利于岩心饼化。因此，需要在高地应力场地通过钻孔获取完整岩心时，钻孔方向须尽量与最大主应力方向平行，以得到钻孔轴向应力场Sv大而径向应力场Sh小的应力场组合，降低钻孔过程中最大拉应力均值。

图11 不同地应力组合最大拉应力贯通线均值随钻孔深度的变化曲线Fig.11 Average value of maximum tensile stress cross line under different geostress against drilling depth

3.3.4 岩心饼裂地应力估算

前文已述，地应力场状态是岩心饼化的最主要诱因，通过对地应力场和岩心饼化相关关系的研究，目前国内外已有部分学者建立了利用岩饼的参数来估算地应力的公式，这些公式有以剪切破坏为理论依据，也有基于拉伸破坏或断裂力学理论而建立。本文将基于拉伸破坏理论，以σT<σta为饼裂判据，通过线弹性有限元计算模型建立地应力估算公式。

对3.3.3节中的计算结果,以钻孔平均应力场Sm=(Sh+Sv)/2为分母进行归一化处理，图12为不同钻孔深度，归一化后径向应力场与最大拉应力均值的关系图。σta/Sm与Sh/Sm呈线性关系，可用式(1)进行表达,其中a,b为拟合参数。

σta/Sm=a(Sh/Sm)+b。

(1)

图12 最大拉应力贯通线均值与径向应力场的关系Fig.12 Relationship between average value of maximum tensile stress cross line with radial stress

将式(1)以Sh,Sv为变量，进行数学转换可以得到式(2)、式(3)。其中参数A,B随钻孔深度变化曲线如图13所示。

σta=(a+b/2)Sh+(b/2)Sv;

(2)

σta=ASh+BSv。

(3)

图13 参数A,B随深度变化曲线Fig.13 Curves of coefficients A and B varying with depth

参数A随钻孔深度的变化曲线形态与最大拉应力贯通线均值随钻孔深度变化曲线一致，参数B与A的比值保持在-0.22左右，因此式(3)可以简化为式(4)的形式。

σta=A(Sh-0.22Sv) 。

(4)

将拉伸饼裂判据代入式(4)有：

σta=A(Sh-0.22Sv)>σT,

(5)

(6)

图14 岩心饼裂时应力场分布Fig.14 Field stress distribu-tion of rock core discing

式(6)为岩心发生饼裂时的应力场组合条件，如图14所示，当Sv,Sh在阴影区内即会出现钻孔岩心饼化现象。

式(6)中的岩石抗拉强度可通过试验获取，参数A随钻孔进深而增大，直到h/D=0.6后基本保持定值，可将A(h/D=0.6)作为临界参数。本文所研究的岩石抗拉强度取值可参考周辉等[19]对锦屏T2b大理岩进行的抗拉试验结果，其值在4～6 MPa范围内，本文取平均值σT(T2b)=5 MPa；A的临界值取基于D=0.06 m的线弹性有限元模型的计算结果，A(h/D=0.6)=0.145。将所取抗拉强度和参数A临界值代入式(6)可有锦屏T2b大理岩钻孔岩心饼化的临界地应力场组合条件，即

Sv<4.55Sh-156.74 。

(7)

对于垂直于洞壁开挖面的钻孔，孔口段的轴向应力场Sv因松弛卸荷，可不予考虑其影响，将Sv=0代入式(7)有锦屏T2b大理岩垂直洞壁钻孔孔口段岩心饼化的临界地应力场条件，即

Sh>34.44 MPa 。

(8)

4 实例验证及应用

4.1 钻孔方向与岩心饼化

前文通过数值模型分析了钻孔的轴向应力场及径向应力场对岩心饼裂的影响，在对7#实验室洞壁进行地应力测试工作中，在同一部位布置了一个水平孔和一个45°仰角的斜孔。其中水平孔与洞壁垂直，相应的钻孔浅表处轴向应力场最小，而径向应力场最大，该应力组合有利于岩心饼化；而当钻孔与洞壁成一定角度时，钻孔轴向应场开始增大同时径向应力场相应地减小，降低了岩心饼化可能性。图15分别为水平孔和45°仰角孔的浅表段岩心，水平孔除了构造及开挖形成的破裂之外，还存在钻孔过程中形成的饼裂；而斜孔不仅无岩饼，其岩心的完整度也明显好于水平孔。

图15 水平孔及45°斜孔孔口段岩心Fig.15 Rock cores in the shallow part of horizontal hole and inclined hole with 45° angle

鉴于以上钻孔方向对岩心饼化影响的理论分析和现象观察，在高地应力场地采用解除法测试浅表地应力时以及统计岩体RQD时，可以采用与开挖面成斜角的钻孔，以降低钻孔过程中岩心饼化的可能性，保证测试数据的有效性。

4.2 平面主应力方向

研究表明鞍形岩饼的凹轴与钻孔径向平面的最大主应力方向一致。本文参考前期的地应力测试资料[20]，通过对典型鞍形岩饼形貌测量来进一步验证。如图16(a)所示，通过切槽解除法完成了2#试验支洞底板的平面主应力大小及方向的测试，其中底板平面最大主应力σH=98.1 MPa，最小主应力σh=55 MPa，最小主应力与洞轴线夹角为6°。

应力测试槽通过圆形钻头连续重叠钻孔成型，因此可通过岩心的缺口部位来确定岩心的原始方位。分别选取垂直及平行洞轴槽中典型的鞍形岩饼(图16(b))并进行表面三维扫描，获得其表面高程数据并绘制等高线，通过等高线的分布可以基本判断鞍形岩饼凹轴的走向，如图16(c)所示，岩饼凹轴的走向基本与试验洞底板的最大平面主应力方向一致。以上分析结果进一步证实了可通过鞍形岩饼的形貌来判断平面主应力方向的可行性。

5 结 论

在对锦屏高地应力部分钻孔岩心饼化特征进行调查统计分析的基础上，总结已有的研究成果，基于岩心张拉饼裂理论进行了钻孔岩心应力分析，主要得到以下结论：

(1)钻孔过程中，随着孔壁应力解除，岩心表面形成的拉应力集中区是饼裂纹触发的诱因，岩饼端面起伏形貌及断裂特征受岩心内部拉应力集中区控制，表现为岩饼端面凹曲形态与拉应力集中区形态一致，断口以对称分布的拉坎为主。

(2)足够大的地应力是岩心饼裂的首要地质环境，地应力越大,使形成的岩饼厚度越小。

(3)岩心饼化程度受钻孔直径、钻孔方向、钻孔深度等因素影响。同一场地的岩饼厚径比基本一致，岩心直径越小，岩饼的厚度越小。

(4)岩心径向轴向应力场与轴向应力场对钻孔岩心中形成的拉应力贡献不同，径向应力场增大促进岩心拉应力增长,而轴向应力场增大使岩心拉应力减小。

(5)鞍形岩饼凹轴方向与岩心径向平面最大主应力方向一致，可通过鞍形岩饼的端面凹轴走向来判断平面主应力的方向。

(6)基于岩心张拉饼裂破坏模式，通过弹性模型分析，可得到岩心饼化时应力场与岩心抗拉强度的关系式，通过该式得到锦屏T2b大理岩垂直洞壁钻孔孔口段岩心饼化的临界地应力场条件为Sh>34.44 MPa。

本文是基于锦屏典型岩心饼化现象进行的初步理论分析，对于高应力场岩心饼化及岩体应力释放的研究,还需更加系统地开展岩心、岩体及地应力场的调查统计工作及理论研究。

[1] OBERT L，STEPHENSON D E. Stress Conditions under which Core Discing Occurs[J]. Society of Mining Engineers of AIME Transactions, 1965，232(3)：227-235.

[2] DURELLI A J，OBERT L, PARKS V J. Stress Required to Initiate Core Discing[J]. Transaction Society of Mining Engineers, 1968，241：1065-1073.

[3] JAEGER J C，COOK N G W. Pinching-off and Disking of Rocks[J]. Journal of Geophysical Research, 1963，68(6)：1759-1765.

[4] DYKE C G. Core Discing: Its Potential as an Indicator of Principal in Situ Stress Directions[C]∥International Society for Rock Mechanics and Rock Engineering, ISRM International Symposium, Pau, France, August 30-September 2, 1989. Rotterdam：A. A. Balkema，1989:1057.

[5] LI Y, SCHMITT D R. Effects of Poisson’s Ratio and Core Stub Length on Bottomhole Stress Concentrations[J]. International Journal of Rock Mechanics and Mining Sciences, 1997，34(5)：761-773.

[6] MATSUKI K, KAGA N, YOKOYAMA T,etal. Determination of Three Dimensional in Situ Stress from Core Discing Based on Analysis of Principal Tensile Stress[J].International Journal of Rock Mechanics and Mining Sciences，2004，41(7)：1167-1190.

[7] KAGA N，MATSUKI K， SAKAGUCHI K. The in Situ Stress States Associated with Core Discing Estimated by Analysis of Principal Tensile Stress[J]. International Journal of Rock Mechanics and Mining Sciences, 2003，40(5)：653-665.

[8] CORTHÉSY R，LEITE M H. A Strain-softening Numerical Model of Core Discing and Damage[J]. International Journal of Rock Mechanics and Mining Sciences, 2008,45(3): 329-350.

[9] 姚宝魁.二滩坝址岩心裂饼现象及其断裂破坏机制[J]. 地质科学，1986，(3)：300-311.

[10] 刘世煌.拉西瓦水电站的岩芯饼化现象[J].西北水电技术，1988，(3):11-18.

[11] 尚岳全，孙 琪.天荒坪电站岩芯饼化机制分析[J].地质灾害与环境保护,1991,2(2):49-52.

[12] 侯发亮，刘 军，卓 光.应力解除时岩芯中的应力状态及饼状岩芯破裂成因分析[J].岩石力学与工程学报, 1986,5(1):61-78.

[13] LIM S S. In-situ Stress Magnitude and Core Disking[D]. Edmonton：University of Alberta，2013.

[14] 钱七虎,李树忱.深部岩体工程围岩分区破裂化现象研究综述[J].岩石力学与工程学报，2008，27(6)：1278-1284.

[15] HAIMSON B C，LEE M Y. Estimating Deep in Situ Stresses from Borehole Breakouts and Core Disking—Experimental Results in Granite[C]∥Proceedings of the International Workshop on Rock Stress Measurement at Great Depth, the 8th International Congress on Rock Mechanics, Tokyo, September, 1995: Rotterdam: A. A. Balkema, 1995:19-24.

[16] SCHMITT D R，CURRIE C A，ZHANG L. Crustal Stress Determination from Boreholes and Rock Cores: Fundamental Principles[J].Tectonophysics, 2012, 580: 1-26.

[17] 李占海,李邵军,冯夏庭,等.深部岩体岩芯饼化特征分析与形成机制研究[J].岩石力学与工程学报,2011,30(11): 2254-2266.

[18] 汪 斌,朱杰兵,邬爱清,等.锦屏大理岩加、卸载应力路径下力学性质试验研究[J]岩石力学与工程学报,2008,27(10):2138-2145.

[19] 周 辉,杨艳霜,肖海斌,等.硬脆性大理岩单轴抗拉强度特性的加载速率效应研究——试验特征与机制[J].岩石力学与工程学报，2013，32(9):1868-1875.

[20] 刘元坤,韩晓玉,汪 洋,等.锦屏深部岩体地应力测试专题报告[R].武汉：长江水利委员会长江科学院，2012.