基于改进极限学习机的风电机组轴承故障诊断
2018-03-16文传博
杨 露, 文传博
(上海电机学院 电气学院, 上海 201306)
大型工业器械结构复杂,控制点众多,一旦发生安全事故将会造成巨大的人身和财产损失。因此,如何根据系统过去和现在的状态诊断系统的故障所在,即故障诊断尤为重要。常见的故障诊断方法有专家系统、支持向量机、人工神经网络等[1]。其中,人工神经网络因其具有强大的非线性逼近功能,且建模难度低,十分适用于复杂过程故障诊断[1]。极限学习机(Extreme Learning Machine,ELM)因其学习速度快、泛化能力好、鲁棒性强等优点[1-5]成为近年来的研究热点,正越来越多地被应用到故障预测[1]、医疗诊断[6]、人脸识别[7]、图像处理[8]等领域。但是,ELM也存在一些自身的不足,如ELM的隐层参数是随机生成的,在一定程度上导致了网络结构的稳定性变差;ELM在求解输出权值时应用到Moore-Penrose(MP)广义逆理论,当输入的样本数据之间存在复共线性关系时,使用MP广义逆方法无法消除复共线性关系,易出现病态解问题,从而导致网络鲁棒性变差、泛化性能和预测精度降低[9]。针对上述问题,学者们提出了一些改进ELM的算法。文献[10]中提出了一种基于粒度划分的在线贯序ELM算法;文献[11]中提出了一种基于Delta检验和混沌优化算法的改进式增量型核ELM算法;文献[12]中提出了一种给增量型ELM隐层输出加上偏置的算法;文献[13]中提出了一种基于差分进化和粒子群优化的混合智能算法,并用其对ELM参数进行优化;文献[14]中提出了一种离散过程神经元网络(DPNN),用量子粒子群(QPSO)对DPNN参数进行训练,并对QPSO中量子旋转门中幅角的更新方式进行改进,最后将改进后的算法与ELM结合,提出QELM-DPNN算法。
风能作为一种清洁的可再生能源,正被大规模地开发和利用。风电机组的轴承是风机主轴、齿轮箱、发电机等旋转设备的主要支撑部件,其工作状态对风机的正常运转有着重要影响,其中旋转机械的故障中约30%都与轴承有关[15]。由于轴承本身润滑不良、装配问题、异物入侵以及恶劣的外部环境、超负荷运转等原因,使轴承成为最易损坏的元件之一。对滚动轴承的早期故障进行诊断,并及时更换损坏轴承,不仅可尽量避免对关联部件的影响,还能减少故障停机,避免因旷日持久地维修及故障引发的事故,减少人力和财力的损失,节约风能发电的成本。
本文在上述研究基础上给出了一种基于自适应混沌粒子群(Adaptive Chaos Particle Swarm Optimization,ACPSO)算法优化的ELM算法,先用ACPSO算法优化ELM的隐层参数,然后,通过MP广义逆求出ELM的输出权值;最后,将该算法应用到轴承故障诊断中。仿真实验表明,相较于ELM算法和PSO-ELM算法,ACPSO优化的ELM算法具有较好的稳定性和较高的分类精度。
1 ELM算法
1.1 基本ELM算法
ELM是在MP广义逆矩阵理论的基础上提出的一种单隐层前馈神经网络的监督学习算法[16]。该算法由单隐层前馈神经网络发展而来,在网络的输入权值和隐层偏置赋值的情况下,即可确定一个具有可逆特性的隐层输出矩阵,完成系统逼近,从而将神经网络训练转化为最小二乘问题,得到隐层输出权值的最小二乘解。
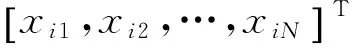
(1)
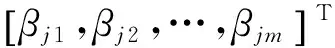
Hβ=T
(2)
式中:H为神经网络的隐层输出矩阵;β为权重输出;T为输出向量。
(3)
(4)
训练单隐层前馈神经网络可以转化为求解一个线性系统Hβ=T,且
β=H†T
(5)
式中:H†为矩阵H的MP广义逆矩阵。由此可知,ELM算法不需要选取输入权值和隐层偏置,也不会出现局部最优解的问题。
1.2 改进的ELM算法
针对ELM网络结构的不稳定性,本文提出了一种改进的ELM算法。对随机生成M组输入权值ω和隐层偏置b利用ACPSO算法进行寻优,将最优的ω和b作为ELM的输入权值ω和隐层偏置b,从而增强网络的稳定性和算法的精度。
随机产生M组输入权值ω和隐层偏置b,将每组ω,b作为粒子群中一个粒子的位置矢量,即xld=[ω,b]。其中:l=1,2,…,M;d=1,2,…,D,D为ω和b的维度之和。利用迭代方式,使每个粒子向自身找到的最好位置和群体中最好位置粒子靠近,从而搜索到ω,b的最优解。在每次迭代中,粒子都要更新速度和位置[17],即
式中:vld=[vl1,vl2,…,vlD]为粒子t的飞行速度,即粒子移动的距离,取值范围为[vmin,d,vmax,d];c1和c2为学习因子,一般取2;r1和r2为[0,1]内的随机数;位置xld的取值范围为[xmin,d,xmax,d];pld为粒子迄今为止搜索到的最优位置;gld为整个粒子群迄今为止搜索到的最优位置;ϖ为惯性权重;ϖmax和ϖmin分别为权值最大值和权值最小值;k为当前迭代次数;kmax为最大迭代次数。
在PSO算法中,每个粒子均代表一个具有一定速度的点,每个粒子均用其各自对应的个体适应度来判断解的优劣。采用仿真结果出错率fld作为网络训练的适应度值,fld越小,则粒子搜索性能越好,
fld=err/Q
(9)
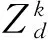
式中:γ为自适应权重;α为给定常数;m为通过混沌搜索算法当前迭代运算中位置更新的粒子数;M为粒子群中粒子总数。
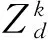
(14)
式中:μ为控制参数,μ∈(2,4],初值zd在各维度上的取值范围为[0,1]。当μ=4时,logistic映射处于混沌态,可产生非周期、不收敛的混沌变量。
与传统的ELM方法相比,ACPSO优化的ELM网络稳定性较高,分类精度有所提高。
2 改进ELM算法在风电机组轴承故障诊断上的应用
ELM可以构造分类器,应用于模式识别领域,其基本思想是逼近一个分类函数把几类数据分类开。构造单一网络的ELM多分类器只需要设定ELM的输出节点数,在进行分类判别时,可通过比较各节点的值来判断该样本的类别,其中,节点值最大者即为该样本的类别,如图1所示。图中,xi(i=1,2,…,n)为输入向量;G(ωj,bj,x)(j=1,2,…,S)为隐层输出向量;ym为输出向量。将样本数据输入到分类器中,由分类器根据不同的输入向量调节隐层参数,使输出类别与实际类别相同,训练好的分类器可用于同类问题的分类处理。
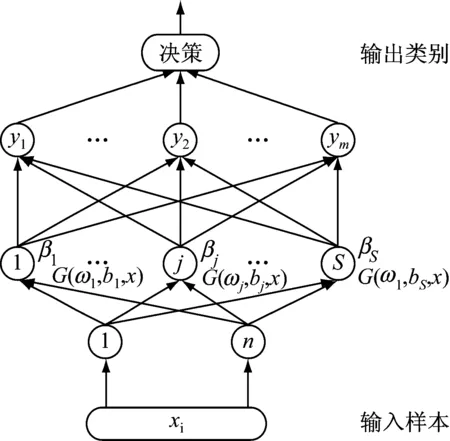
图1 单一模型的极限学习机分类器
对风电机组轴承故障进行分类实验,选取轴承最常见的故障有内圈故障、外圈故障、保持架故障。用1表示正常状态, 2表示内圈故障,3表示外圈故障,4表示保持架故障。将轴承故障特征数据集用ACPSO-ELM分类器进行训练,得到轴承的故障诊断模型,如图2所示。
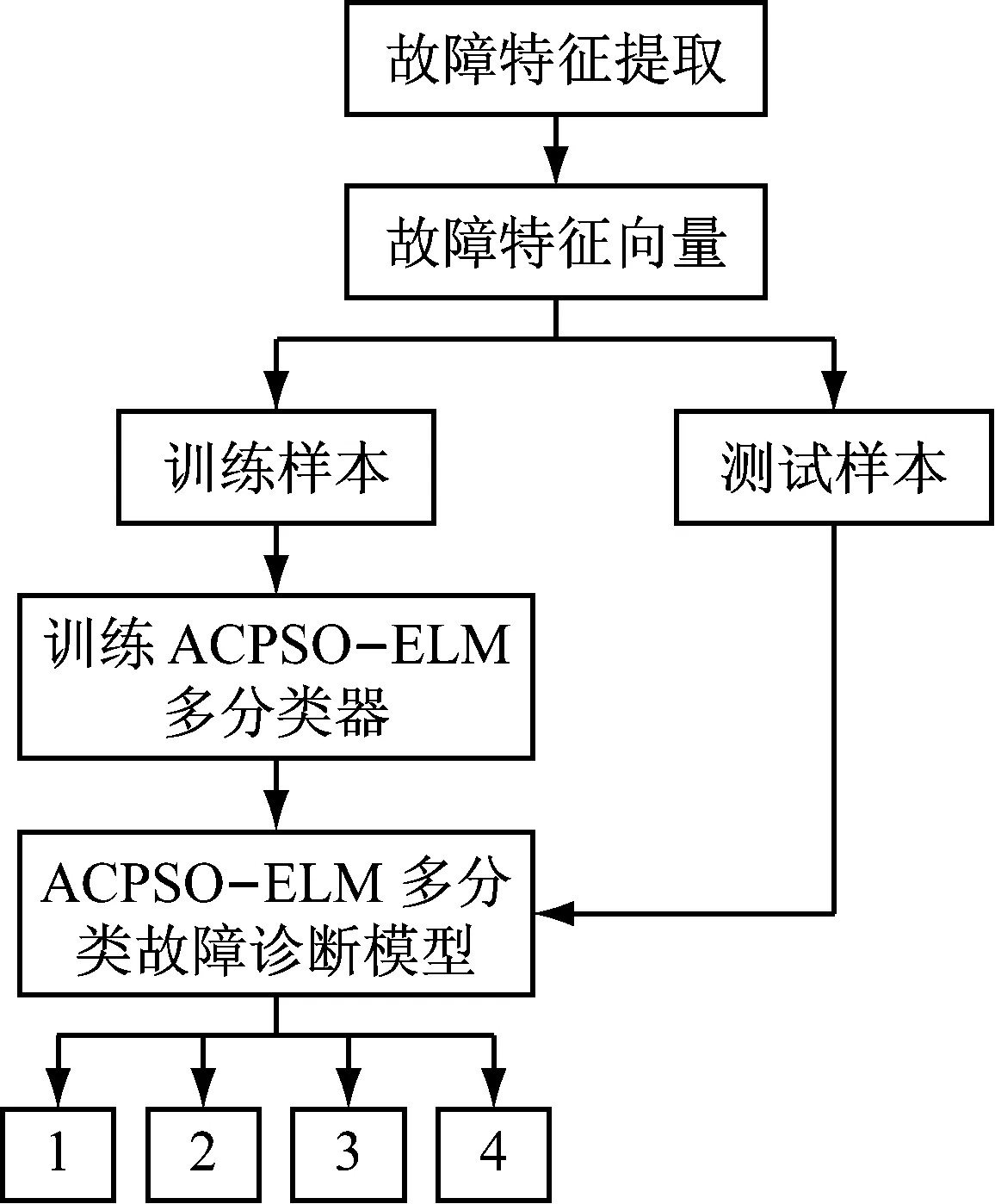
图2 基于ACPSO-ELM的风电机组轴承故障诊断
基于ACPSO-ELM的风电机组轴承的故障诊断步骤如下:
(1) 对轴承故障数据进行归一化处理,将输入数据标准化到[-1,1],目标数据标准化到[0,1];并将故障数据随机分成训练数据集和测试数据集两组;
(2) 建立基于ACPSO的ELM神经网络拓扑结构,设置神经元个数及隐藏节点数,选中激活函数;
(3) 初始化种群,即令k=0,初始化α,λ;
(5) 根据式(10)计算各粒子适应度,并设置种群个体最优位置pld和全局最优位置gld;
(6) 利用式(11)对gld加入混沌变量pc;然后利用式(7)~(9)更新所有粒子的速度和位置;
(7) 根据式(10)计算所有粒子的适应度值,更新pld和gld;
(8) 判断是否达到最大迭代次数;若是,则停止迭代;否则,转步骤(4)继续迭代。
迭代结束时的gld即为最优(ω,b),根据式(3)~(6)计算输出权重β,根据式(2)计算输出矩阵,对比实际输出和计算输出,判断故障诊断是否正确,并计算故障诊断正确率。
3 仿 真
由于风电机组现场故障难于采集,本文采用美国凯斯西储大学轴承数据中心[20]的实验数据进行风电机组轴承故障诊断。试验轴承型号为6205-2RS JEM SKF,采样频率为12 kHz,电动机转速为1 772 r/min,电动机负载为735 W,故障直径为0.177 8 mm,对振动信号进行分析,轴承外圈故障采样点设置在垂直于负载区位置上,振动信号采用驱动端加速度数据。
对振动信号进行小波包降噪处理,其中,使用的小波包函数为sym6,分解层数设置为5,在频域分析中,采样点数设置为214=16 384。图3所示为小波包降噪前、后轴承部分振动信号的比较。
对消噪后的振动信号进行时域和频域分析,分别提取时域分析中的脉冲指标I、裕度指标L、峭度指标K和频域分析中的功率谱重心指标Fc、功率谱方差Fv、谐波因子J作为振动信号的故障诊断特征量R=[I,L,K,Fc,Fv,J]。由于各特征量量纲不同,故在训练前需对各特征量进行归一化处理,即
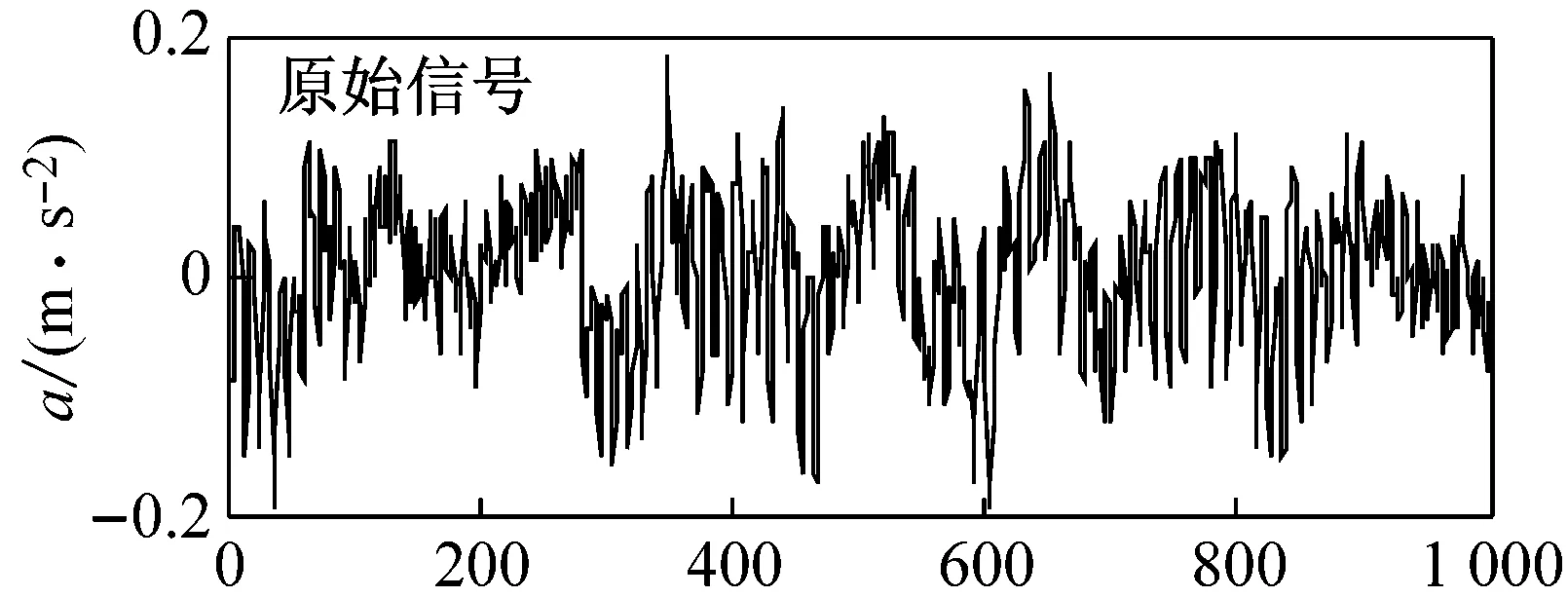
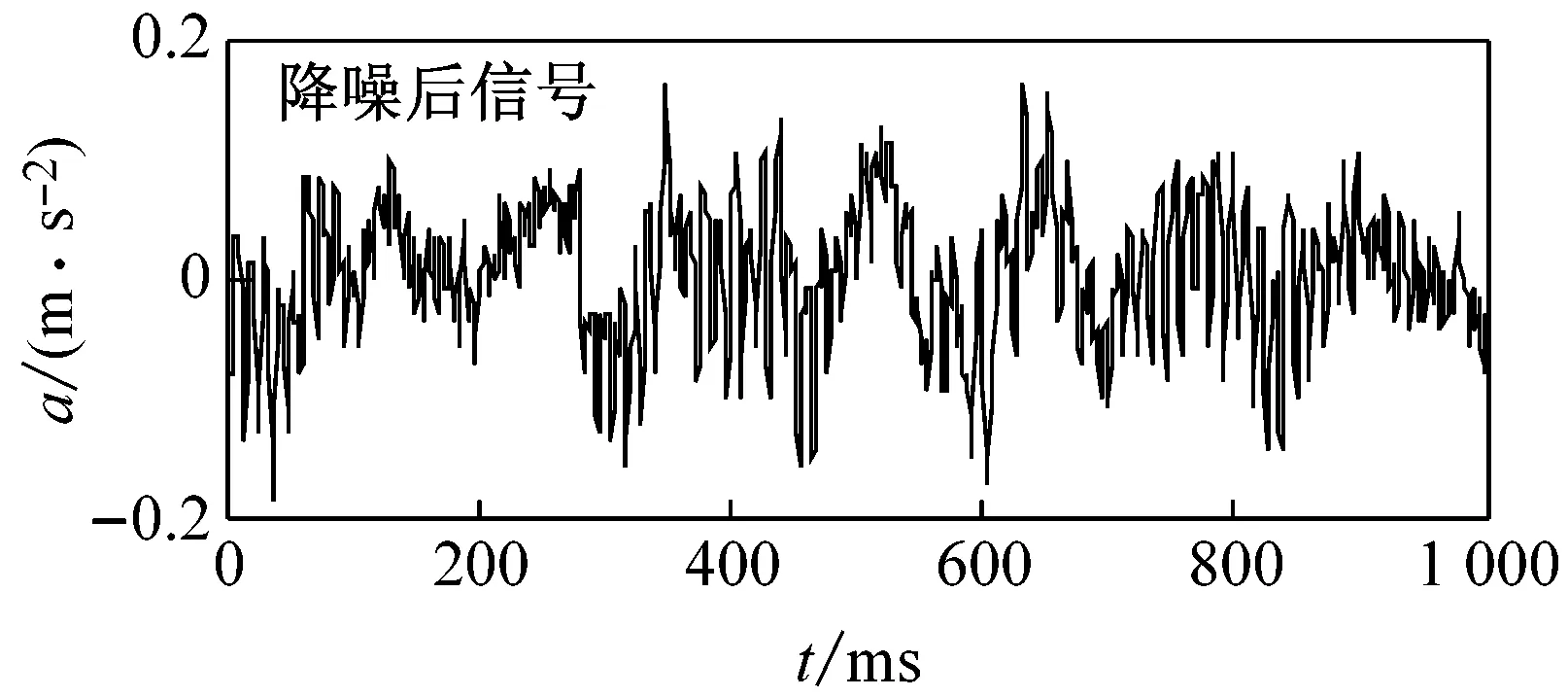
(a) 轴承正常
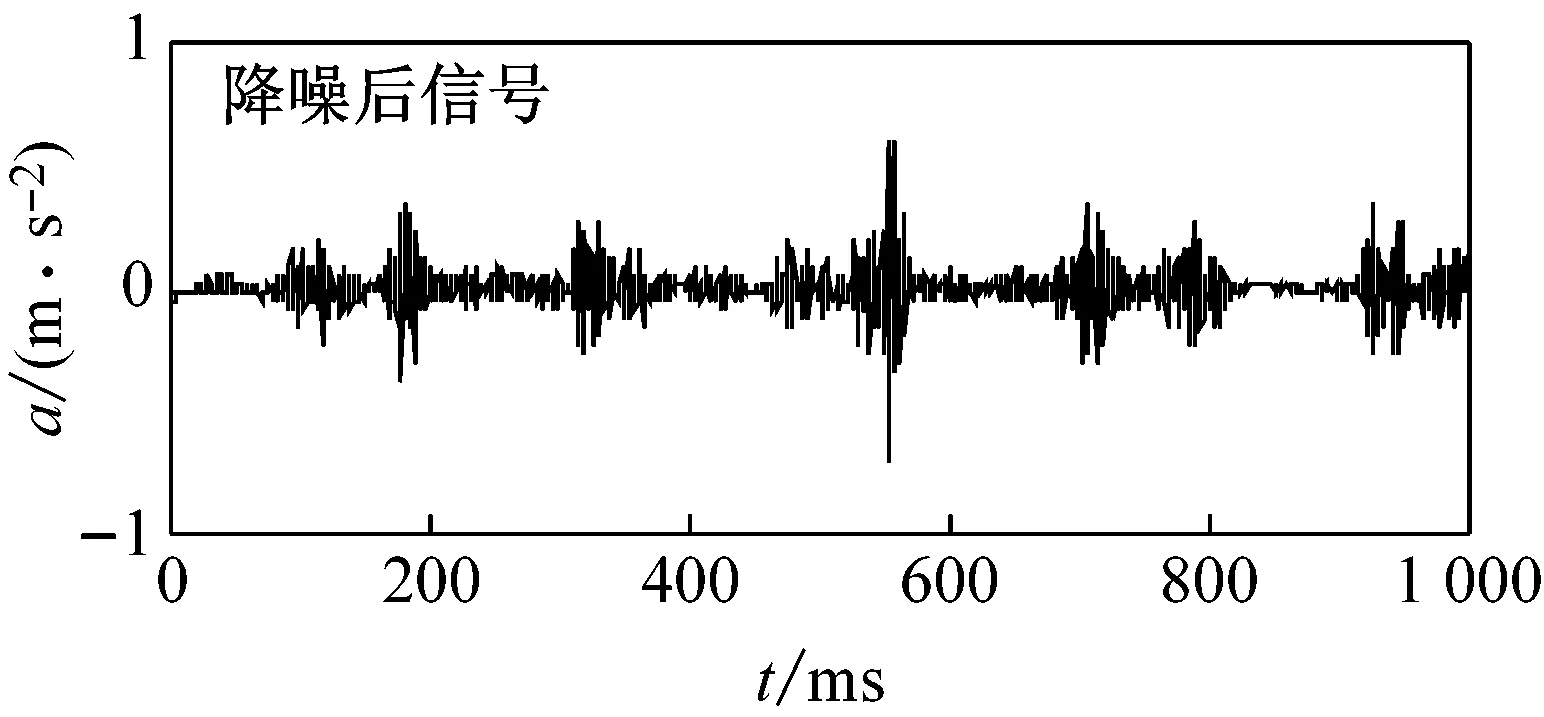
(b) 轴承内圈故障

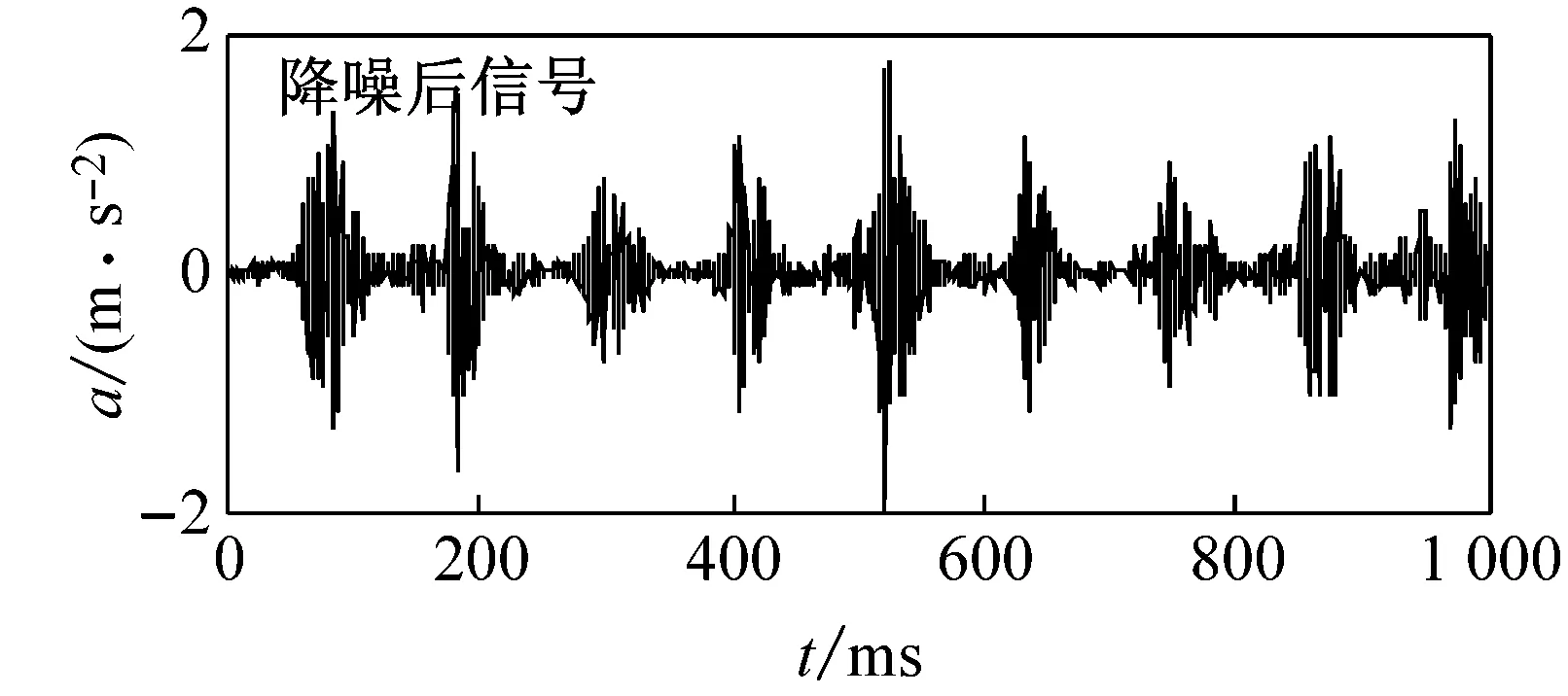
(c) 轴承外圈故障
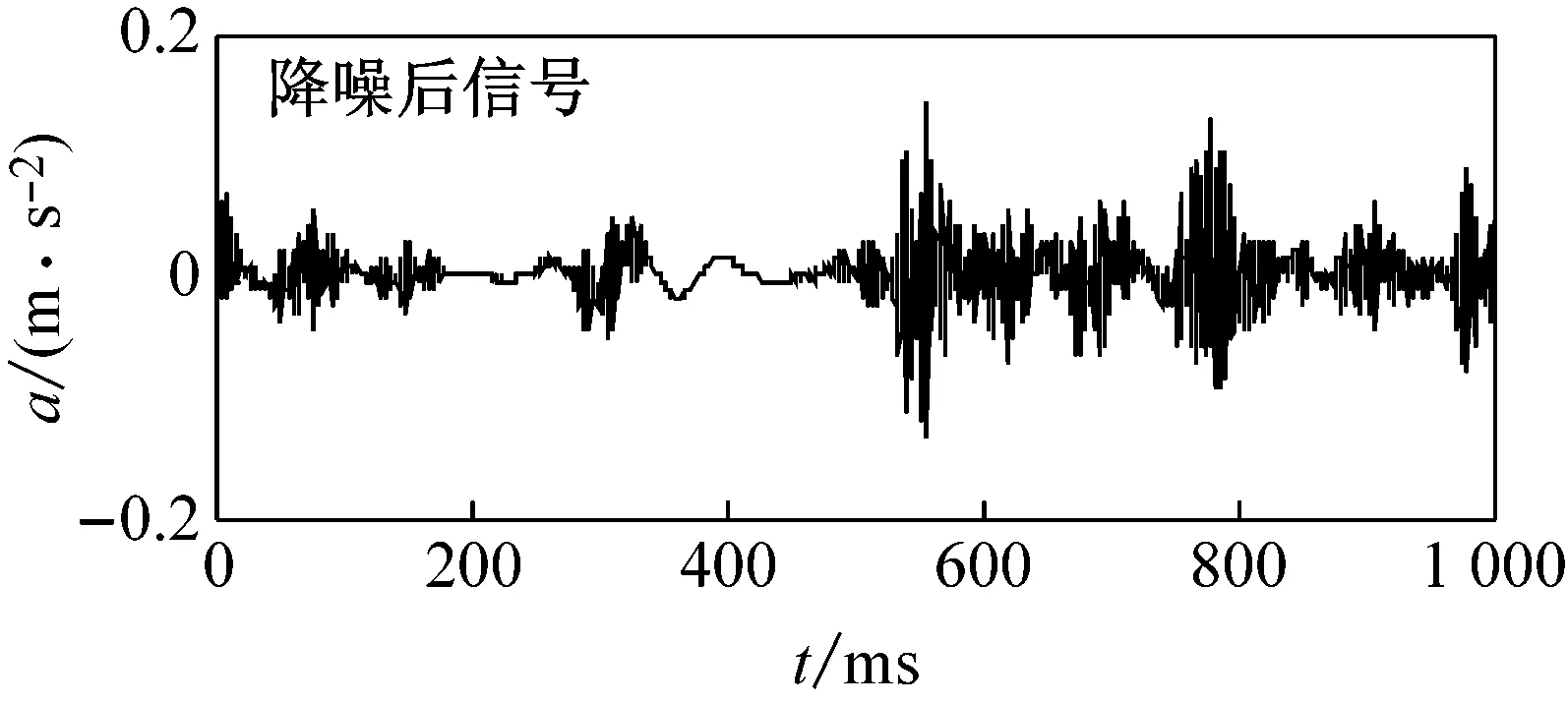
(d) 轴承滚动体故障
图3轴承振动信号的消噪效果图
(15)
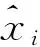
归一化后的所有数据都在[-1,1]内,将其作为故障诊断系统样本的输入向量。表1所示为归一化后的轴承故障诊断的部分样本数据。
为验证ACPSO-ELM方法的有效性,本文分别用ELM、PSO-ELM、ACPSO-ELM对处理后的轴承故障数据随机选取168组进行训练,然后,在这168组轴承数据中随机抽取120组数据作为训练样本,剩余48组作为测试样本,进行仿真实验。所用实验粒子群参数设置为粒子群数M=20,最大迭代次数Kmax=50,学习因子c1和c2均设置为1.5,输入权值ϖmax=0.9,ϖmin=0.4,位置xi的取值范围为[-1,1],在ACPSO-ELM中α=0.5,λ的初始值设置为1.0。图4给出了3种算法的故障预测精度对比。
由图4可见,ELM的故障预测结果随隐层节点数的增大而存在较大的震荡性,实验结果不稳定;在ELM中加入PSO算法对参数进行优化后,故障预测结果不再随隐含层节点数的增大而大幅度震荡,说明PSO算法能够有效地提高了ELM算法的稳定性,且ELM预测的精度也得到提高,突出了参数优化的重要性;与PSO-ELM算法相比,ACPSO-ELM算法具有相同效果,且性能略优于PSO-ELM算法。
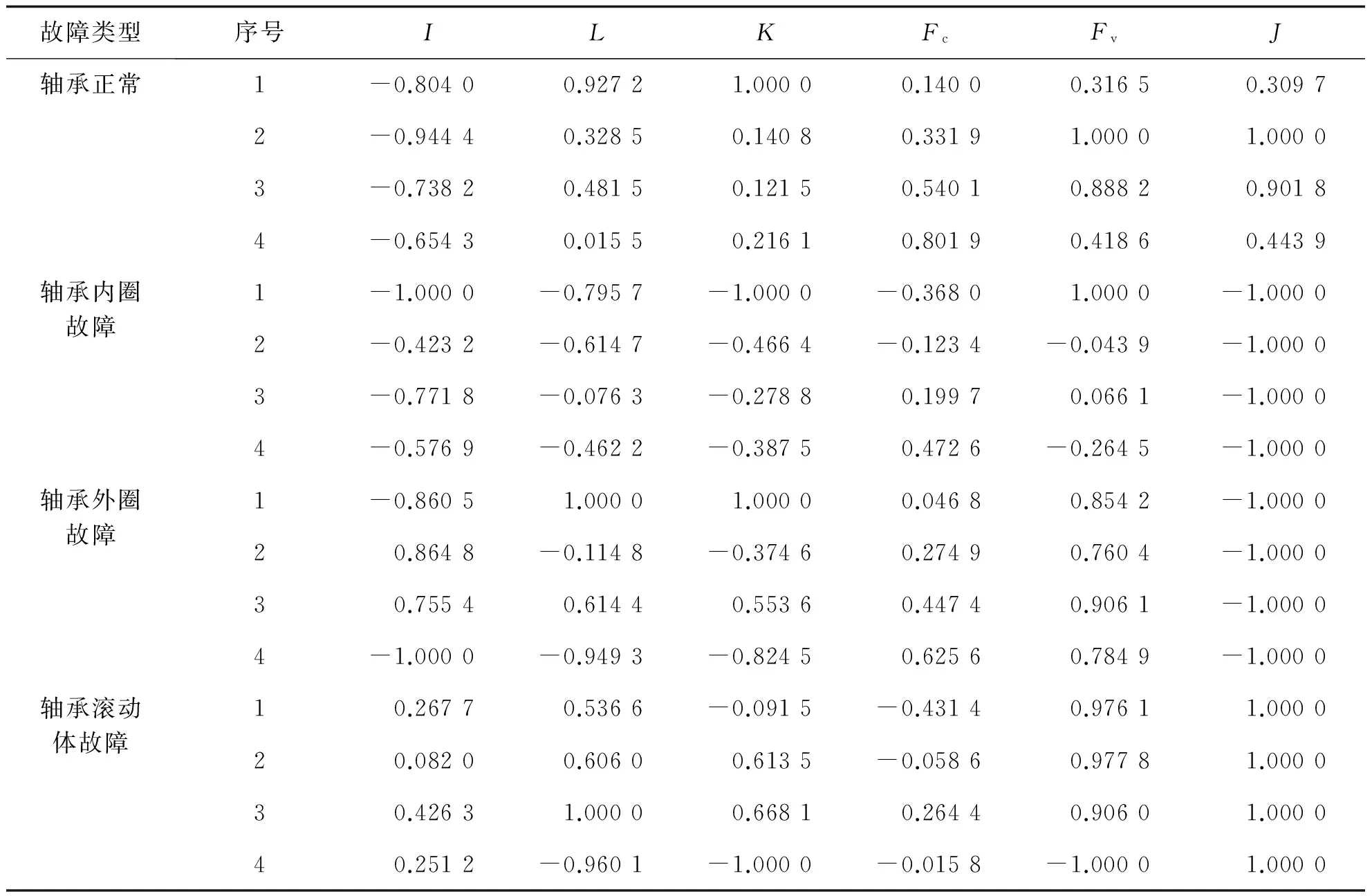
表1 归一化的部分轴承故障样本数据
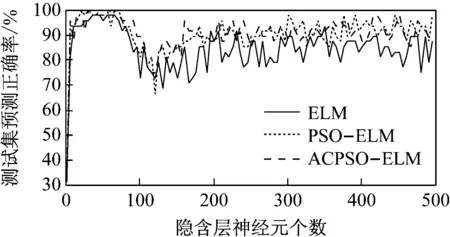
图4 3种算法的故障预测精度对比
为了更加清晰地对3种算法的分类效果进行比较,对比3种算法的优劣,将隐含层节点数设置为定值,使程序运行10次,取10次结果精度的平均值作为各算法的精度进行比较,其中,程序每次运行时的训练集和测试集都是随机选取的。表2给出了隐含层节点数为80时各算法的分类效果对比。
由表2可以看出,ACPSO-ELM算法的运行时间要比PSO-ELM算法的运行时间略长,这是由于在ACPSO-ELM算法中,每次迭代都需对全局最优位置加入自适应混沌变量。虽然ACPSO-ELM算法的运行时间比PSO-ELM算法略长,但其在分类精度上要略高于PSO-ELM算法,说明本文所研究的基于ACPSO-ELM的风电机组轴承故障诊断方法是有效的,且故障诊断的准确率较ELM及PSO-ELM算法略高。
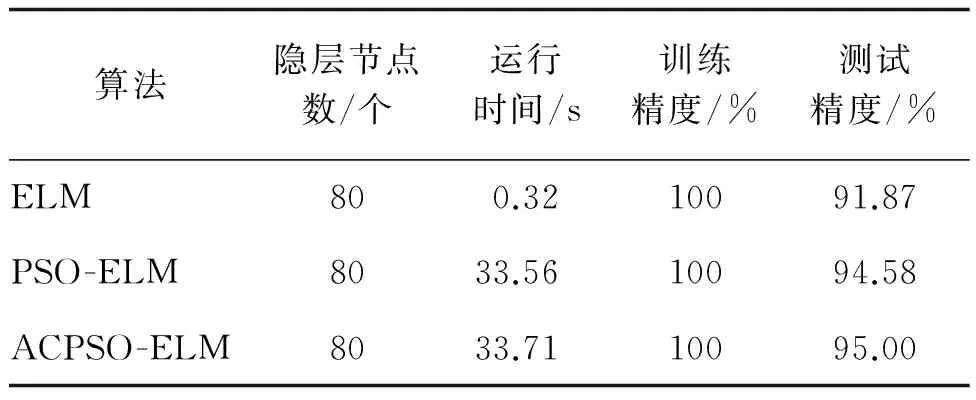
表2 几种算法的运行时间和精度对比
综上所述,在风电机组轴承故障诊断上,ACPSO-ELM算法无论是在分类精度上还是稳定性上都优于ELM算法及PSO-ELM算法。
4 结 语
针对ELM算法分类精度低、网络结构不稳定等情况,本文研究了ACPSO-ELM算法,通过ACPSO算法对ELM网络的隐层参数进行优化,以提高分类精确度、增强网络结构的稳定性。将该方法应用到风电机组轴承故障诊断上,在风电机组轴承故障诊断上,与已有的ELM和PSO-ELM进行比较可知,本文提出的ACPSO-ELM算法具有较高的分类精度和更好的稳定性。
[1] 徐圆,叶亮亮,朱群雄. 基于动态记忆反馈的改进ELM故障预测方法应用研究[J]. 控制与决策, 2015, 30(4): 623-629.
[2] HUANG Guangbin, ZHOU Hongming, DING Xiaojian, et al. Extreme learning machine for regression and multiclass classification [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B, 2012, 42(2):513-529.
[3] YEU C W T,LIM M H, HUANG Guangbin, et al. A new machine learning paradigm for terrain reconstruction [J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(3):382-386.
[4] HUANG Guangbin, CHEN Lei, SIEW C K. Universal approximation using incremental constructive feedforward networks with random nodes [J]. IEEE Transactions on Neural Networks, 2006, 17(4): 879-892.
[5] HUANG Guangbin, ZHU Qinyu, MAO K Z, et al. Can threshold networks be trained directly? [J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2006, 53(3):187-191.
[6] HUANG Guangbin, ZHU Qinyu, SIEW C K. Extreme learning machine: Theory and applications [J]. Neurocomputing, 2006, 70(1/2/3):489-501.
[7] 王博林,闫德勤,楚永贺. 基于稀疏排列的LPP和ELM的人脸识别[J]. 微型机与应用, 2016, 23: 42-45.
[8] 李作仁,王佳玉,安雨桐,等. 极限学习机在图像分割中的应用[J].电脑知识与技术, 2016, 12(3): 207-209.
[9] 王改堂,李平,苏成利. 岭参数优化的ELM岭回归学习算法[J]. 信息与控制, 2011, 40(4): 497-506.
[10] 毛文涛, 田杨阳, 王金婉,等. 面向贯序不均衡分类的粒度极限学习机 [J]. 控制与决策, 2016, 31(12): 2148-2154.
[11] 王超, 王建辉, 顾树生, 等. 改进式混合增量极限学习机算法[J]. 控制与决策, 2015, 30(11): 1981-1986.
[12] 宋绍剑, 向伟康, 林小峰. 增量型极限学习机改进算法 [J]. 信息与控制, 2016, 45(6): 735-741.
[13] 林梅金, 罗飞, 苏彩红, 等. 一种新的混合智能极限学习机 [J].控制与决策, 2015, 30(6): 1078-1084.
[14] 刘志刚, 许少华, 李盼池. 基于QPSO和极限学习机的离散过程神经网络及学习算法 [J]. 控制与决策, 2016, 31(12): 2241-2247.
[15] 王致杰, 徐余法, 刘三明,等. 大型风力发电机组状态监测与智能故障诊断 [M]. 上海: 上海交通大学出版社, 2013:49.
[16] HUANG Guangbin, ZHU Qinyu, SIEW C K . Extreme learning machine: A new learning scheme of feedforward neural networks [C]//2004 International Joint Conference on Neural Networks. Budapest, Hungary: IEEE, 2004: 985-990.
[17] SHI Yuhui, EBERHART R. A modified particle swarm optimizer [C]// Proceedings of IEEE International Conference on Evolutionary Computation. Anchorage: IEEE, 1998:69-73.
[18] LIU Hongwu. An adaptive chaos particle swarm optimization [C]//ISECS International Colloquium on Computing, communication, Control, and Management. Sanya, China:IEEE, 2009:254-257.
[19] 陈晓青,陆慧娟,郑文斌,等. 自适应混沌粒子群算法对极限学习机参数的优化 [J].计算机应用,2016,36(11):3123-3126.
[20] CASE WESTERN RESERVE UNIVERSITY. Bearing data center seeded fault test data [DB/OL]. [2017-07-12]. http://csegroups.case.edu/bearingdatacenter/pages/download-data-file.
