基于粒子群优化自抗扰无刷直流电动机控制
2018-03-16杨凯亦
黄 伟, 杨凯亦
(上海电力学院 自动化工程学院, 上海 200090)
直接转矩控制作为一种转矩闭环控制方法,能瞬时控制转矩。近年来,在无刷直流电动机(Brushless DC Motor,BLDCM)上的应用成为研究热点。文献[1-2]中研究了适用于BLDCM直接转矩控制算法;文献[3-4]中研究了BLDCM磁链自控直接转矩控制算法,省去了磁链控制环,控制结构更为简单。目前,典型 BLDCM双闭环控制方案的转速环大多采用PI控制,内环则采用PI或滞环控制。PI控制可以避免高频、大幅度扰动的影响,但缺少了微分作用,系统难以同时满足快速性及无超调的要求。文献[5-6]中研究了基于自抗扰控制器(Active Disturbance Rejection Controller,ADRC)的BLDCM控制方案,将BLDCM等效为2个非线性系统构成的串联对象,设计2个一阶ADRC对BLDCM的内、外环进行控制,抑制了BLDCM运行时的转矩波动,提高了BLDCM转速的控制精度;但是,ADRC需要整定的参数较多,且没有完整的参数整定原则[7],大大增加了整定的工作量,不便于实际运用。文献[8-10]中研究了模糊ADRC,利用模糊算法解决参数调整困难、控制器繁杂的问题;但是,模糊算法无法定义控制目标,且简单的模糊信息处理反而会降低系统的控制精度。文献[11-14]中介绍了线性自抗扰控制与非线性自抗扰的特点,分别结合经验法、带宽法、动态参数整定、时间尺度及智能优化算法给出了ADRC的参数整定方法,但大多数整定方法都受工程实际的限制或太过繁琐而难以实施。
针对上述问题,本文研究了采用转速环自抗扰控制BLDCM直接转矩的方案:电动机等效为转速子系统与转矩子系统,采用ADRC控制转速环、滞环控制转矩环。自抗扰控制将被控系统转化为积分串联型,系统的动态复杂性和不确定性可以通过输入、输出各阶导数的变化规律及外扰对它们的影响反映,利用状态观测器从系统控制量输入及被控对象输出的反馈来估计扰动并消除。同时,针对ADRC参数整定较为困难的问题,采用简单高效的改进粒子群算法(Particle Swarm Optimization,PSO)[15],选取适当的性能指标函数来进行参数整定,提高其实际应用性,仿真实验验证了该方法的可行性及有效性。
1 BLDCM数学模型
以两极BLDCM两两导通为例,作如下假设:
(1) 忽略电动机铁芯饱和,不计涡流损耗和磁滞损耗;
(2) 不计点数反应,气隙磁场分布近似是平顶宽度为120°电角度的梯形波;
(3) 忽略齿槽效应,电枢导体连续、均匀分布于电枢表面;
(4) 驱动系统逆变电路的功率管和续流二极管均有理想的开关特性。
永磁BLDCM数学模型为[2]
(1)
式中:uA,uB,uC为三相定子电压;Rs为定子电阻;L,M分别为定子自感和定子间互感;iA,iB,iC为三相定子电流;εA,εB,εC为三相反电势。
电动机的电磁功率为
Pe=εAiA+εBiB+εCiC
(2)
不计转子的机械损耗,电磁功率全部转化为转子动能,则
Pe=Tev
(3)
式中:Te为电磁转矩;v为电动机转速。
由式(2)和式(3)可得
Te=(εAiA+εBiB+εCiC)/v
(4)
引入电动机运动方程[2],有
(5)
式中:TL为负载转矩;B为阻尼系数;J为电动机的转动惯量。
式(1)~(5)共同构成了BLDCM完整的数学模型。
2 自抗扰BLDCM直接转矩控制
2.1 转速环ADRC控制器设计
2.1.1 转速跟踪微分器 经典PID控制器是基于误差反馈来消除误差的,而实际系统的输出惯性不能突变至给定值,若为了加快变化过程而增大增益kP,则容易使初始控制量过大而产生超调。跟踪微分器的作用在于安排合适过渡过程,降低起始误差,转速离散跟踪微分器为
(6)
式中:v1,v2分别为过渡过程的给定信号和速度;r为速度因子;h为积分步长;fhan(x1,x2,r,h)为该离散系统最速控制综合函数;l为离散系统最速控制函数值[7],即
(7)
式中:x1,x2为原点初始点;y为半抛物线在等时区(限定步内能到达原点的所有初始点全体)之外部分所在直线;d为函数线性区间;d0为等时区外限定边界;a,a0为构造函数使等时区外确定曲线与折线折点重合。
转速跟踪微分器输出两个量:① 跟踪参考转速的信号; ② 过渡过程的速度变化,即微分量。用转速跟踪微分器安排过渡过程的关键在于能够实时得到给定信号值,而与其变化规律无关,若r较小,则跟踪微分器输出可以光滑地跟踪给定值;若r较大,则跟踪微分器输出较为接近原始输入,r的取值取决于受控对象的承受能力。
2.1.2 转速扩张状态观测器 由式(5)可得到
(8)
对其进行变换,得到
(9)
式中:b为补偿因子;Tg为转速环给定转矩。
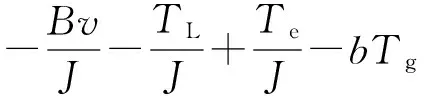
(10)
式中,u为控制量。对其建立状态观测器,则有
(11)
式中:e为观测误差;z1为v的观测值;z2为g(v)的观测值;β1,β2,α1,δ1为控制器参数;fal(e,α,δ)为幂次函数;
(12)
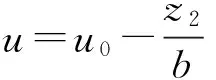
(13)
2.1.3 非线性反馈控制律 在进行数值仿真时,为避免高频颤振现象的出现,取fal(·)作为反馈律,在原点附近具有线性区间[-δδ],则
(14)
式中:v1为跟踪微分器跟踪转速;α2,δ2,β3为控制器参数。
由于u0是根据误差e1来决定的控制纯积分器串联型对象的控制量,转速系统在经过扩张状态观测器观测后可得到g(v)的估计值z2,因此,实际控制量还需要通过调节补偿因子对扰动估计值进行补偿。
跟踪微分器、扩张状态观测器及非线性反馈律共同组成了转速系统ADRC。由于将BLDCM分成了转速与转矩两大系统,设计外环转速系统时将内环转矩系统当作传递函数为1,由Tg直接控制转速系统,转速系统ADRC控制结构图如图1所示。图中,vg为电动机给定转速。
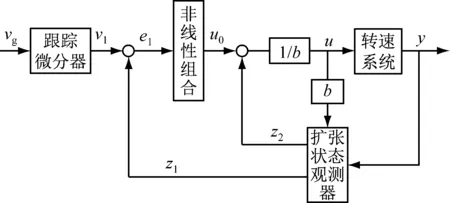
图1 转速系统ADRC控制结构图
2.2 转矩环滞环控制
本文中,BLDCM采用两相导通模式,用“1”“0”分别代表逆变器的开关导通和开关判断状态。由逆变器的6个开关状态可以得到对应的电压矢量U1(100001),U2(001001),U3(011000),U4(010010),U5(000110)及U6(100100),分布图如图2所示。图中,θr为转子磁链ψr与α轴的夹角。
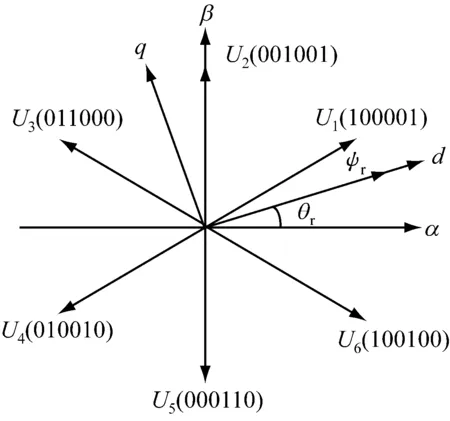
图2 空间电压矢量分布图
根据电动机原理,BLDCM的转矩为
Te=km|ψs||ψr|sinθ
(15)
式中:km为转矩系数;|ψs|,|ψr|分别为定子、转子磁链空间矢量幅值;θ为定、转子磁链之间夹角。
将转子磁链矢量方向作为d轴,q轴超前d轴90°建立旋转坐标系d-q,则
Te=km|ψsq||ψr|
(16)
式中:ψsq为定子磁链ψs在q轴的分量。
ψs是定子电动势矢量的积分,在忽略定子电阻压降影响的情况下,其在空间中按作用的电压矢量方向运动,即
(17)
式中:Us为定子电压矢量;is为定子电流。
由式(17)可知ψs的变化与施加Us方向一致,而通过调节ψs使其垂直于ψsq,可以补偿转矩偏差,因此,电压矢量的选择以随转子位置变化垂直于ψr方向的分量最大为依据。Us在q轴上对应的夹角θ值如表1所示。
由式(5)可得到BLDCM的运行转速,通过对其积分可得到电动机转子的实时角度,并划分转子扇区,结合电压矢量空间分布得到磁链自控直接转矩控制电压空间矢量的选择,如表2所示。表中,τ为转矩调节器状态,1为需要增大转矩,0为需要减小转矩。

表1 电压矢量作用下定、转子磁链夹角

表2 磁链自控直接转矩控制电压空间矢量选择
ψs在空间电压矢量作用下的轨迹如图3所示。
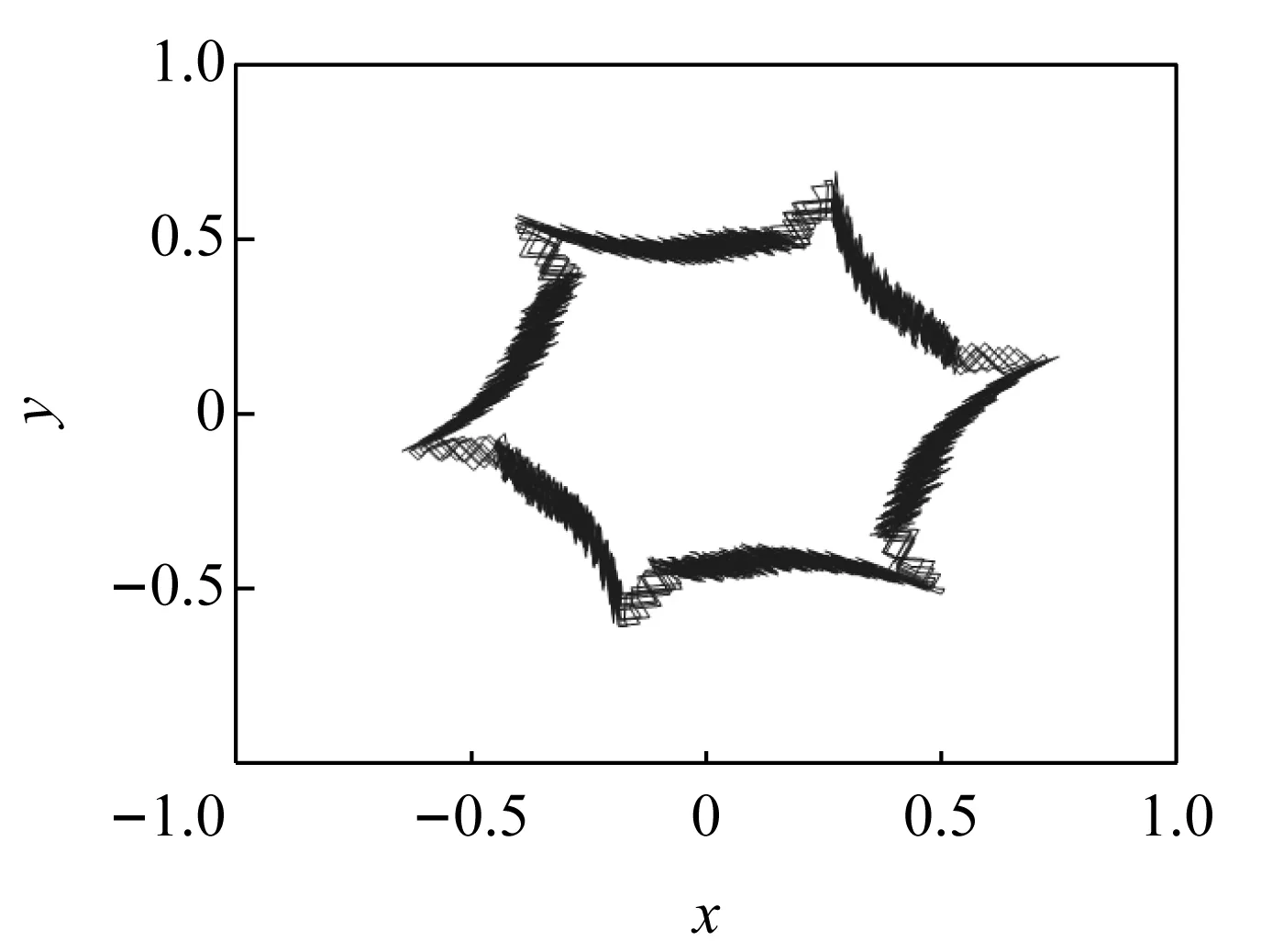
图3 定子磁链轨迹图
滞环控制作为一种非线性控制,结构简单响应速度快,参数鲁棒性好,在PWM控制中应用广泛。两点式转矩调节器基于滞环控制原理的设计如图4所示。图中,ΔT为参考转矩Tref与电动机实际输出转矩T之差;εm为转矩调节器设定范围。
当ΔT≥εm,T

图4 两点式转矩调节器
3 改进PSO参数整定
ADRC较经典PID控制器,具有更多的需整定参数。跟踪微分器参数可以根据系统的可承受能力来调节;对于扩张状态观测器参数,文献[12]中给出了通过系统带宽的方法来进行整定,但是,该方法将非线性反馈变为了线性反馈,降低了控制器性能,且非线性控制反馈律也只能确定一定的参数区间。目前,ADRC的参数并没有较为完整的参数整定原则。
搜索优化算法可以在给定约束的条件下寻求变量,使目标性能达到最优,较好地解决ADRC参数整定较为困难的问题;PSO就是其中一种简单高效的优化算法,是一种基于迭代的优化算法[12],系统初始化一组随机位置粒子,所有粒子都有一个目标函数决定的适应值,通过粒子自身及同伴经验来改变速度,从而达到最优适应值。
3.1 自适应权重
虽然PSO简单高效,但容易陷入局部最优解,且收敛速度较慢。其权重决定了粒子对当前速度的继承量,适当的取值可以使粒子具有均衡的探索能力和开发能力。为了平衡PSO算法的全局搜索能力及局部改良能力,引入非线性动态惯性权重系数公式[16]:

(18)
式中:w为惯性权重;wmax,wmin分别为最大、最小权重值;f为粒子适应度;favg,fmin分别为当前所有粒子的平均适应度和最小适应度。
w随着f的改变而改变,当f趋于一致或趋于局部最优时,w增加;当f较为分散时,w减小;同时,对于f较优的粒子,其惯性权重因子减小,从而保护了该粒子,而对于f较差的粒子,其w增加,使得该粒子能靠向较好地搜索区域。
3.2 适应度函数
为获取满意的过渡过程动态特性,一般采用误差的绝对值时间积分(Integral of Absolute Error,IAE)性能指标作为参数选择的最小目标函数;同时,为避免控制量过大,还会加入控制输入的平方项[16],即
(19)
式中:F为性能函数指标;tu为上升时间;w1,w2,w3,w4分别为各项指标权重。
虽然该方法较好地考虑到了系统的绝大多数性能,但是,IAE的缺点在于各项参数在性能指标上的反应不明显,从而延长整定过程。
时间乘绝对值误差积分(Integrated Time and Absolute Error,ITAE)在各种积分误差指标中选择性最好,其特点在于动态响应超调量较小,且调节时间较短。本文在大量仿真验证的基础上,给出了一种新的基于ITAE的适应度函数取法,即
(20)
式中,ts为调节时间。
图5给出了利用IAE和ITAE进行适应度函数参数选取的迭代结果。
由图5可见,基于ITAE的适应度函数的粒子群能更快收敛,且参数变化在性能指标上反应明显,从而加快整定过程。

(a) IAE
图5利用IAE和ITAE进行参数整定的迭代结果
4 系统整体结构与仿真分析
图6所示为基于PSO优化ADRC的BLDCM控制系统结构图。

图6 控制系统整体结构图
BLDCM具体参数见表3所示。

表3 电动机参数
在Matlab/Simulink中建立转速环自抗扰BLDCM直接转矩控制仿真模型,并在Matlab中使用改进PSO算法对ADMC参数进行整定。表4所示为ADRC中相关模块的取值范围。
设定参考转速为400 r/min,电动机反电势系数为43 mV/(rad·s-1),初始负载1 N·m,仿真时间0.2 s,进行仿真,并与PI控制方法进行比较。
图7所示为PI控制与ADRC控制下BLDCM的转速响应比较。两种控制方法都以电动机最大输出能力启动。由图可见,在ADRC控制下,v几乎无超调就达到了设定值,进入稳态,与PI控制相比快15 ms。PI控制下的v波动为(0.3±0.05) r/min,而ADRC控制下的v波动仅为(0.1±0.05) r/min。可见,ADRC控制下的转速精度得到明显提高。

表4 ADRC控制器参数取值模块

图7 PI控制与ADRC控制下的转速曲线
图8所示为PI控制与ADRC控制下的电动机输出转矩的变化。由图可见,在PI控制下,Te变化剧烈,这是由于PI控制不能根据趋势进行预先调节;而在ADRC控制下,由于ADRC根据输入、输出反馈及其微分量提前对扰动进行处理,因此,转矩的波动被限制在较小范围内。
当t=0.1 s时,对BLDCM突加3 N·m的负载转矩,图9所示为负载转矩突变时PI与ADRC控制下的电动机转速。由图可见,在负载转矩突变的情况下,PI控制下的转速在达到稳态前有一定程度振荡,达到稳态的时间较长;而ADRC合理地提取了微分信号,利用扩张状态观测器,可以得到电动机的状态和扰动的实时作用量。通过非线性反馈,使得响应不仅更为迅速,而且几乎无振荡,较好地提高了系统的适应性和鲁棒性。
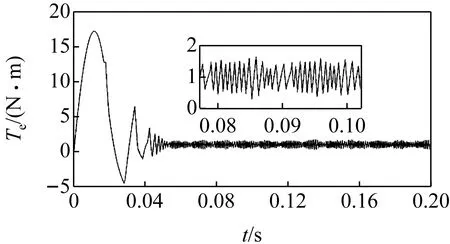
(a) PI控制

(b) ADRC控制
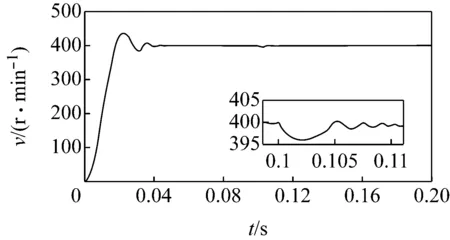
(a) PI控制

(b) ADRC控制
5 结 语
本文研究了基于ADRC的BLDCM转矩控制,提出了一种新型BLDCM控制方案:转速环自抗扰控制、转矩环滞环控制,简化了控制系统的复杂性;同时,结合改进PSO算法研究了一种新的适用于ADRC控制器参数整定的性能指标函数,减少了控制器参数整定的时间,提高了其实际应用性。仿真结果表明,该方案可以有效解决传统PI控制调速时存在的转速超调与振荡问题,提高了电动机稳态时的控制精度;在负载变化时,控制器能迅速调节,使系统有较强的抗干扰能力。
[1] LIU Yong,ZHU Z Q, HOWE D. Commutation torque ripple minimization in direct torque controlled PM brushless DC drives [J].IEEE Transactions on Industry Applications, 2007, 43(4): 1012-1021.
[2] 夏长亮, 张茂华, 王迎发, 等. 永磁无刷直流电机直接转矩控制 [J]. 中国电机工程学报,2008, 28(6):104-109.
[3] 高瑾, 胡育文, 黄文新, 等. 六边形磁链轨迹的无刷直流电机直接自控制 [J]. 中国电机工程学报,2007, 27(15):63-69.
[4] NAIR D S, JAGADANAND G, GEORGE S. Direct torque control with duty cycle control strategy for permanent magnet motors with non-sinusoidal back EMF [C]// 2016 IEEE International Conference on Industrial Technology. Taipei, Taiwan: IEEE, 2016:141-146.
[5] 夏长亮, 李正军, 杨荣,等. 基于自抗扰控制器的无刷直流电机控制系统 [J]. 中国电机工程学报,2005,24(2):82-86.
[6] 夏长亮, 俞卫, 李志强. 永磁无刷直流电机转矩波动的自抗扰控制[J].中国电机工程学报,2006,26(24):137-142.
[7] 韩京清. 自抗扰控制技术 [M].北京:国防工业出版社,2008:220-312.
[8] 李孟秋,汪亮,黄庆,等. 自抗扰参数模糊自整定无刷直流电机控制研究 [J].湖南大学学报(自然科学版),2014,41(5):71-78.
[9] 饶选辉,刘卫国. 基于模糊自抗扰的无刷直流电机直接转矩控制研究 [J].微电机,2014,47(5):36-40,92.
[10] 陈增强,程贇,孙明玮,等. 线性自抗扰控制理论及工程应用的若干进展 [J].信息与控制,2017,46(3):257-266.
[11] 葛立明,李宗刚,王世伟,等. 基于调节/观测时间的自抗扰控制器参数整定 [J].控制与决策,2017,32(7):1334-1337.
[12] 李杰,齐晓慧,万慧,等. 自抗扰控制:研究成果总结与展望 [J].控制理论与应用,2017,34(3):281-295.
[13] 李杰,齐晓慧,夏元清,等. 线性/非线性自抗扰切换控制方法研究 [J].自动化学报,2016,42(2):202-212.
[14] 代志纲,岳巍澎,隋晓雨,等. 自抗扰控制技术的原理剖析 [J].新型工业化,2015,5(1):49-58.
[15] 武雷. 自抗扰控制器参数自学习算法及其应用研究 [D]. 西安:西安电子科技大学,2013:12-18.
[16] 龚纯,王正林. 精通MATLAB最优化计算 [M].北京:电子工业出版社,2009:279-282.
