基于精英策略改进的混合蛙跳算法

江泽昌， 刘天羽， 吴 星， 王义东

(上海电机学院 电气学院，上海 201306)

混合蛙跳算法(Shuffled Frog Leaping Algorithm, SFLA)最早是由Eusuff等[1]于2003年提出的，是一种模仿自然界生物行为而产生的基于种群智能后启发式的全局优化方法。但是，SFLA和其他智能算法一样容易收敛到局部最优，且存在着初始种群不均匀、求解精度不高、收敛速度不够快的缺点[2-3]。

鉴于此，研究者们对SFLA进行了大量研究。文献[4]中通过对SFLA的改进，重新定义了青蛙的觅食机制和进化迭代公式，改善了算法的局部搜索和全局搜索能力。文献[5]中通过对学习的策略产生初始种群，在进化过程中嵌入了差分进化，对复杂函数优化使其具有较强地求解能力。文献[6]中通过理想的搜索策略，使最差个体青蛙向最好个体青蛙学习，且在搜索过程中引入2个加速因子，提高了搜索速度。文献[7-8]中采用随机分组的策略，在最差学习的过程中引入Minkowski距离，避免了算法陷入局部极小，加快了收敛速度。文献[9]中引入柯西变异算子，使算法跳出局部最优。文献[10]中将模糊算法和混合SFLA相结合。文献[11-12]中引入差分算法，使SFLA跳出局部最优和避免早熟。文献[13]中对原始算法添加了变异算子，通过模糊控制器调节变异算子的规模，动态地调整变异算子在解空间的搜索范围、不同阶段和候选解分布的演化过程。上述文献只是对子群中最差青蛙进行了更新改进，并没有对全局最优青蛙进行改进。

针对SFLA在后期收敛速度慢、易于陷入局部最优、且精度低等问题，本文研究了一种改进的混合SFLA。由于在局部搜索中，最差青蛙只是向最优的青蛙学习，故引用精英策略对最差青蛙的位置进行更新，使最差青蛙在向最优青蛙学习的同时，也向本子群中较好青蛙学习；引入了柯西变异算子，增大了全局搜索能力，提高了搜索效率和算法的收敛速度；针对全局最优青蛙很少有机会进化的问题，引入了Minkowski距离，使全局最优青蛙既能向局部其他青蛙方向进化，也能向局部最优青蛙进化，提高了全局最优青蛙的质量。利用5个典型函数对改进后的SFLA和SFLA进行仿真实验，结果表明，改进后的SFLA具有较快的收敛速度，能避免早熟，且优化精度高。最后，对改进的SFLA进行了收敛性分析。

1 SFLA的基本原理

SFLA是模拟青蛙在觅食的过程中，通过群体间的相互合作与竞争相互结合，以实现群体进化的目的。本文以函数的最小值为例说明SFLA的基本步骤：设群体青蛙的种群规模为M，且在d维空间里第i个个体的坐标xi=(xi1,xi2,…,xid)(i，d∈N)，计算个体的适应值，然后按照从大到小顺序排列。将整个种群划分为S个局部子群，每个局部子群中有N只青蛙，即

M=SN

在降序排列的过程中，把排列好的个体平均分配到S个局部子群中去，在指定的局部迭代次数Ne内进行搜索，若满足全局迭代次数maxGE，则停止此次搜索，输出全局最优值；否则，将全部青蛙混合重新计算。

在SFLA中，若局部青蛙产生的新个体优于局部子群中的最差青蛙时，则用新个体来代替局部最差青蛙，因此，在多次替换后产生的新个体必然优于之前的最差青蛙，即在多次迭代中，会使整体中局部子群的青蛙得到进化。若局部子群中产生的新个体不优于局部子群里的最差青蛙时，就用全局最优解Xg来代替局部子群中最好青蛙Xb。其具体的最差青蛙更新策略为

2 一种改进的SFLA算法

2.1 引入精英策略改进最差青蛙

精英策略的基本思想是为了保留住最适应的个体而产生的，目标就是为了将最优解的信息传入到下一代[14]。

在基本SFLA中，局部子群中的最差青蛙只向该子群中的最优青蛙学习，最差青蛙被限制在当前位置与子群中最优青蛙的线性区域中。本文借鉴精英策略，保留子群中的最优青蛙，以防止最优青蛙向较坏方向变异而造成群龙无首，继而出现退化的现象。选择每组中的最差青蛙让其以自身为原点，以到该组中最优青蛙的距离为半径进行360°搜索，并提高搜索速度，使最差青蛙向该子群中较好青蛙学习，且在学习过程中保证自身不退化。

2.2 引用柯西分布变异算子

SFLA在后期的搜索中，很容易陷入局部收敛的情况，为避免该情况的发生，本文引入柯西分布变异算子，使算法在后期跳出局部最优。

柯西分布是概率论与数理统计中的一类常见的分布，其中一维柯西分布的函数为[15]

(3)

式中：x为随机变量；t为常数。

当t=1时，式(3)为标准的柯西分布函数。图1所示为标准柯西分布概率密度函数曲线。

图1 标准柯西分布概率密度函数曲线

由图可见，曲线的两端长扁形状且趋于零，因此，利用柯西分布可以避免改进的SFLA在后期易陷入局部最优的情况。利用柯西分布随机变量生成函数

η=tan[(ξ-0.5)π]

(4)

式中，ξ为[0，1]上的随机变量。

考虑上述因素，提出了一种改进的算法，其更新策略为

2.3 全局最优蛙改进策略

在基本SFLA中，在最差青蛙的进化过程中，全局最优的青蛙几乎不进化。实验证明[7]在进化过程中，全局最优地位会保持很多代，造成算法的寻优速度变慢，且容易出现早熟现象。Minkowski距离是欧氏几何空间中的广义距离度量，提供了丰富、灵活的度量选择[16]。由于全局最优青蛙在位置上很少进化，为增加其进化的机会，本文利用Minkowski距离，使全局最优青蛙向局部子群中其他最优青蛙和除了最差青蛙以外的其他青蛙进行学习，以提高青蛙质量，其更新策略为

Xg=rand()c1M(Xg,Xj)+c2(Xg-Xbj)

(8)

j∈N

式中：Xj为局部除了最差青蛙以外的其他青蛙；Xbi为子群中最优青蛙；M(Xg,Xj)为Xg向其他子群除最差青娃以外学习的Minkowski距离；c1与c2为更新的权值。

改进后的SFLA算法流程图如图2所示。

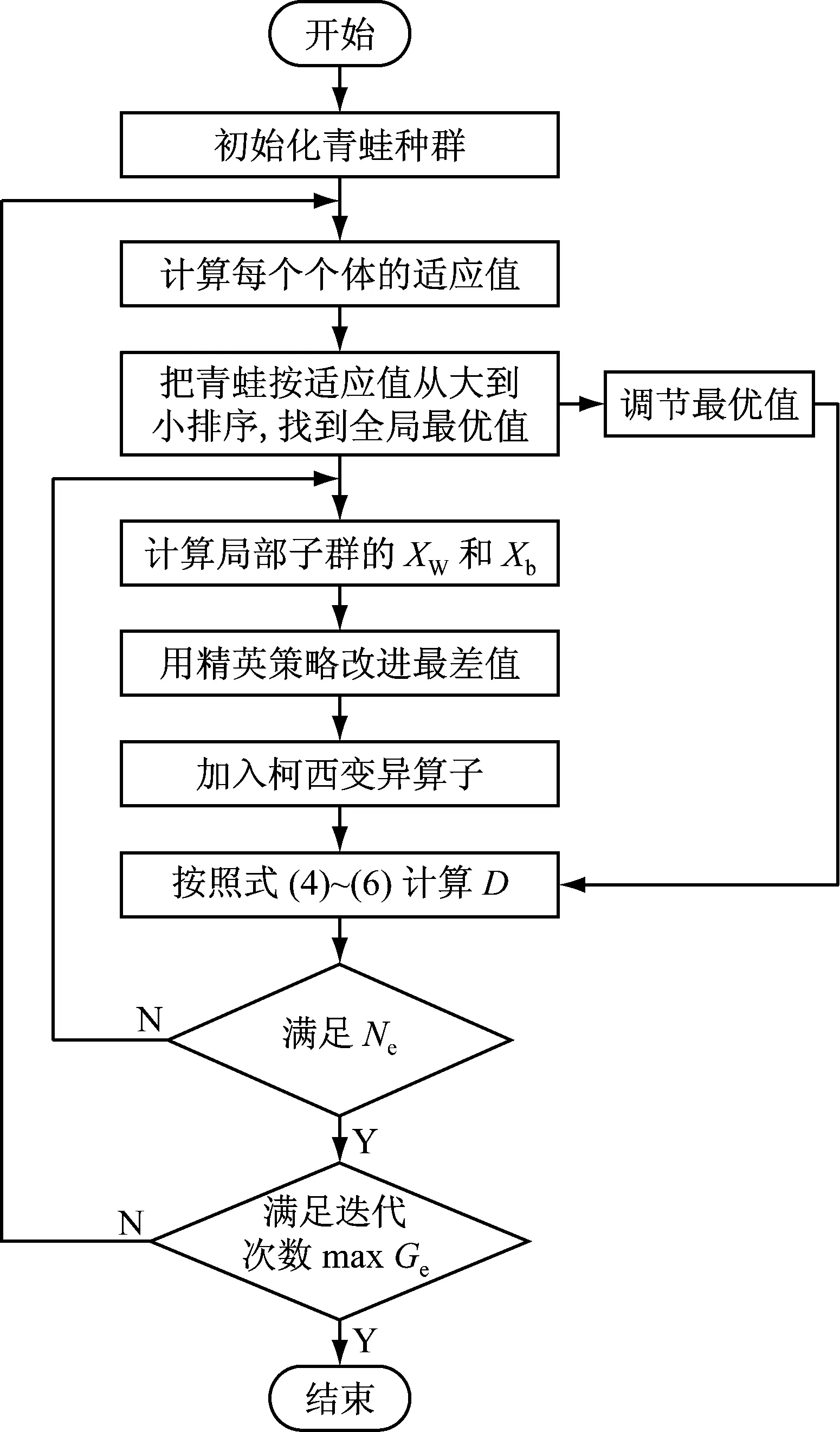
图2 改进后的ACSFLA的算法流程图

3 改进算法的验证

为验证改进策略和新算法的有效性，利用5个典型函数，即Sphere，Rosenbrook，Rastrigin，Griewank，Schaffer f7作为实验对象，采用Matlab7.1编程，在Intel处理器5-3210M(4GB内存)中、Win7操作系统下进行了大量的实验仿真。为增加对比性，本文所有的公共参数均设置相同，其中，M=1 800，S=30，迭代次数Ne=100。各函数的表达式和搜索范围如表1所示。

用上述5种函数对改进后的SFLA和基本SFLA进行仿真比较，所有实验独立运行40次，Ne=100，表2所示为2种算法的仿真实验结果的平均值和方差。由表2可见，改进后的SFLA对测试函数的仿真优化结果，无论是其最优解还是平均值，都较基本SFLA的要小，可见，由于引入了精英策略和Minkowski距离后，使最差青蛙的进化得到了保证，也提高了全局最优青蛙进化的机会，因此，改进后的SFLA较基本SFLA具有更好的优化效果；同时，改进后的SFLA获得的平均值与标准差都比基本SFLA的小，说明改进后的SFLA较基本SFLA在精度上有了明显提高。

表1 测试函数

表2 2种算法对测试函数的仿真优化结果比较

由于改进后的SFLA算法较基本SFLA算法在仿真过程中存在着许多偶然因素，本文利用这2种算法对5种测试函数分别迭代100次和1 000次，运行40次后得到函数最优解的运行曲线如图3所示。由图可见，无论是哪种函数，改进后的SFLA较基本SFLA的收敛速度都要快，而且随着迭代次数的增加，改进后的SFLA的收敛性得到了明显提高，并跳出了基本SFLA局部收敛，使后期收敛速度慢的问题得到了解决。

4 改进后SFLA的收敛性分析

本文借鉴文献[17]对SFLA收敛性的分析，对改进的SFLA进行分析，其证明过程如下。

由式(5)～(7)可得第k次迭代后，

(9)

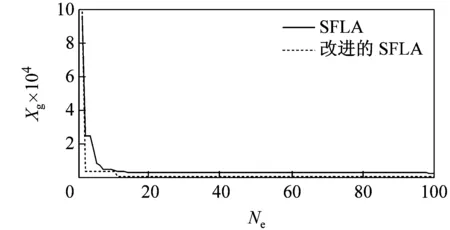
(a)Sphere函数迭代100次

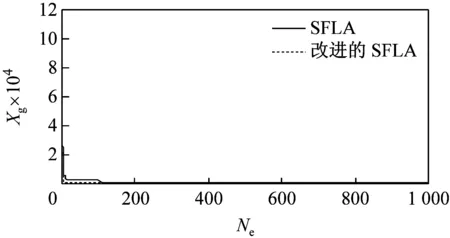
(b)Sphere函数迭代1 000次

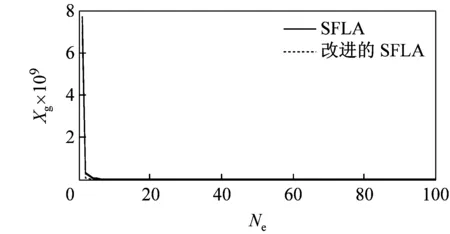
(c)Rosenbroock函数迭代100次

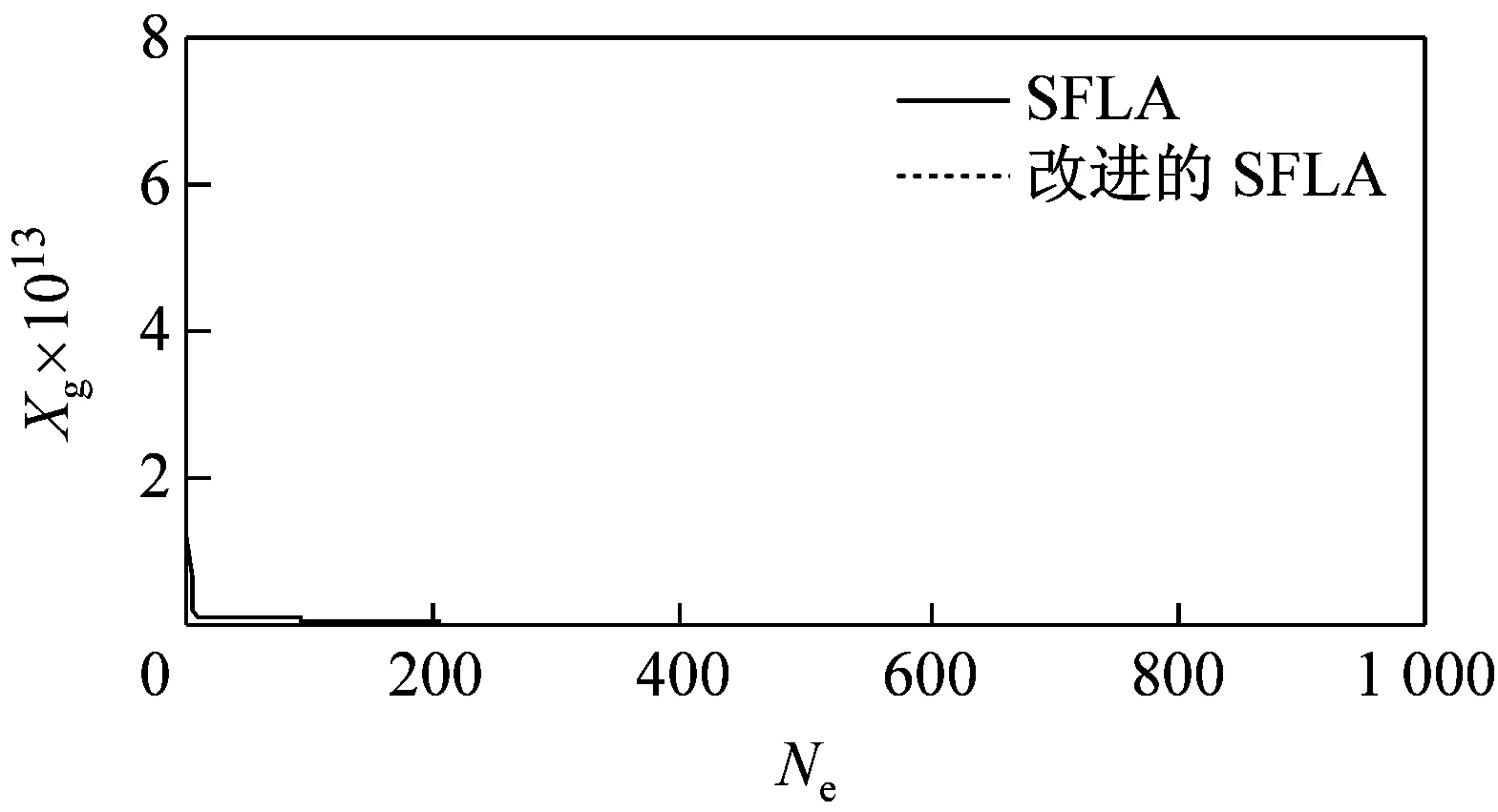
(d)Rosenbroock函数迭代1 000次

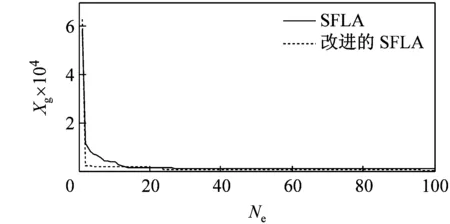
(e)Rastrin函数迭代100次

(f)Rastrin函数迭代1 000次

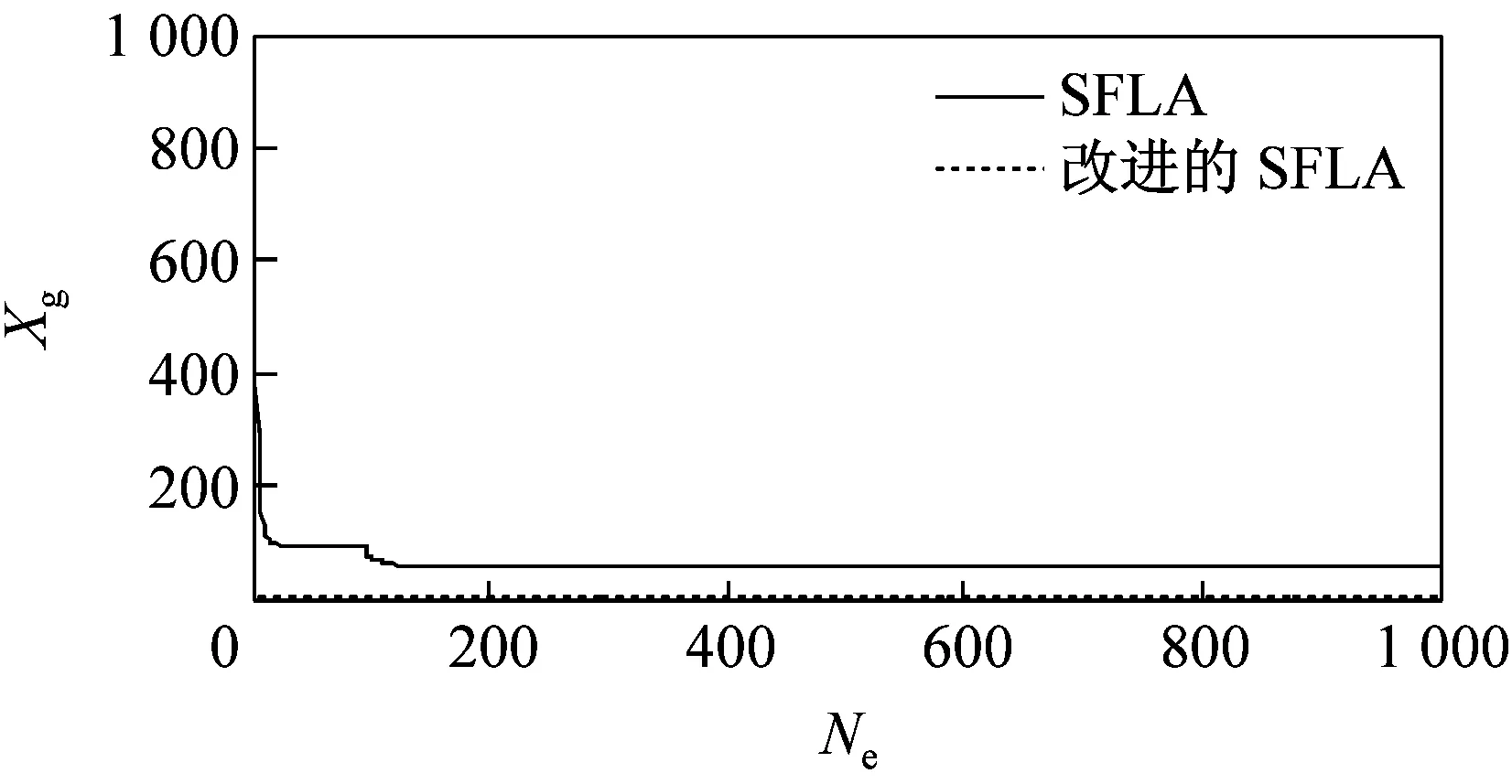
(h)Griewank函数迭代1 000次

(i)Schaffer f7函数100次

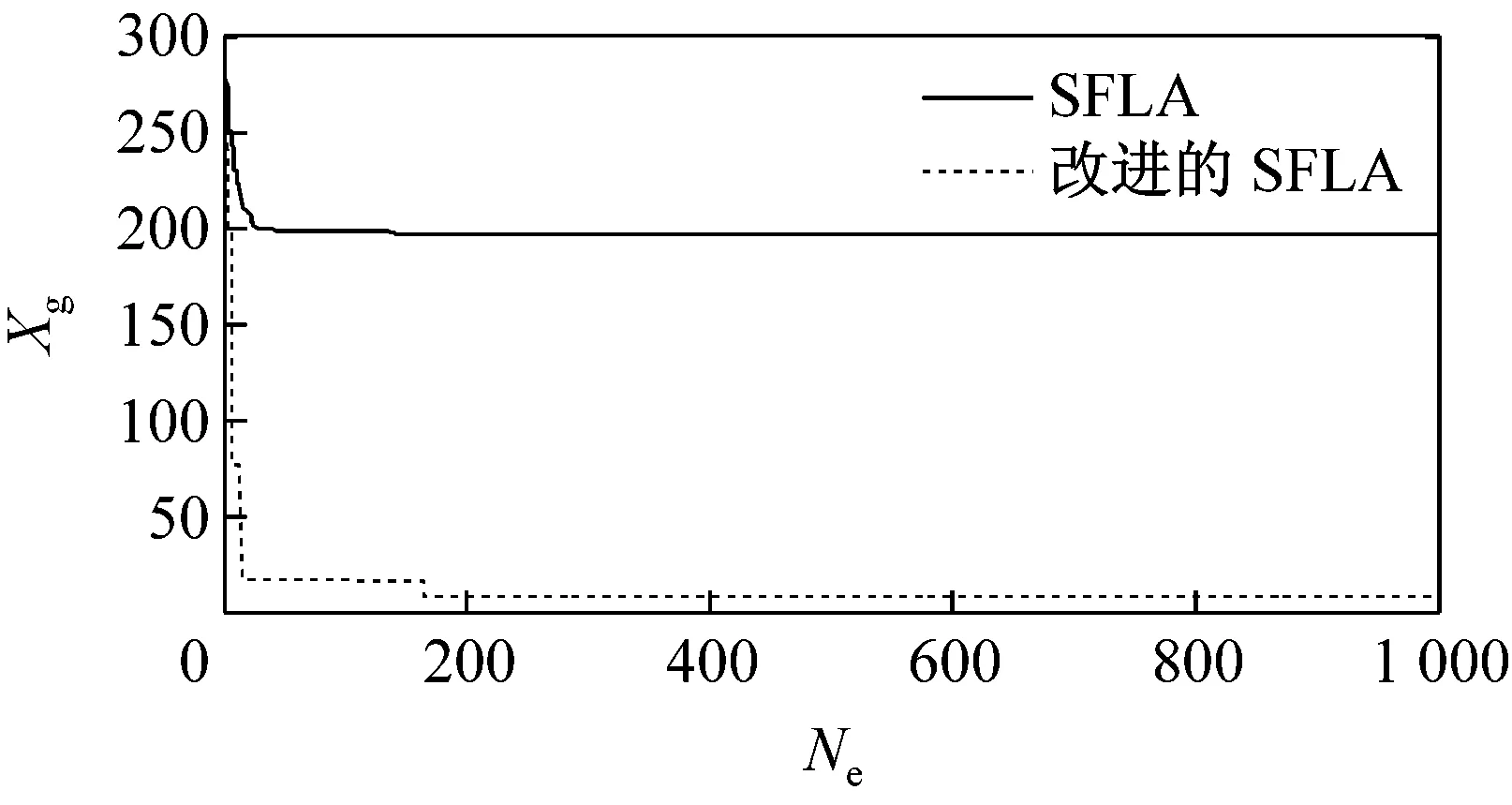
(j)Schaffer f7函数1 000次

而第k+1次迭代后，

(10)

将式(9)与(10)相减

ΔXk+1=Xk-Xk-1， Δe=(ejθ′-ejθ)

可得

(15)

分别以进化k次和k+1次的青蛙为圆心，在(0°,360°)的搜索范围内搜索，得到它们的差值Δe，再与式(7)联合，可得

(16)

5 结 语

针对基本SFLA在后期收敛速度慢和易于陷入局部收敛的问题，研究了基于精英策略的改进SFLA，通过引入精英策略对最差青蛙进行改进，引入柯西分布变异算子改进了搜索策略，并利用Minkowsk距离提升了全局最优青蛙优化的机会；通过对常用的5个测试函数进行仿真测试，结果表明，改进的SFLA具有较快的收敛速度，能够避免早熟，且优化精度高。最后，通过对改进的SFLA进行收敛性分析，其收敛性可以以等比数列进行分析。

[1] EUSUFF M, LANSEY K, PASHA F.Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization [J].Engineering Optimization, 2006, 38(2):129-154.

[2] 贺毅朝,曲文龙,许冀伟.一种改进的混合蛙跳算法及其收敛性分析 [J].计算机工程与应用,2011,47(22):37-40.

[3] 苏仟.混合蛙跳算法研究与改进 [D].西安：西安电子科技大学,2014：19-20.

[4] 赵红星,常小刚.一种改进的混合蛙跳算法 [J].兰州交通大学学报,2017,36(1):51-56.

[5] 赵鹏军,刘三阳.求解复杂函数优化问题的混合蛙跳算法 [J].计算机应用研究,2009,26(7):2435-2437.

[6] JABALLAH S, ROUIS K, ABDALLAH F B, et al. An improved shuffled frog leaping algorithm with a fast search strategy for optimization problems [C]//IEEE International Conference on Intelligent Computer Communication and Processing. Cluj Napoca, Romania：IEEE,2014:23-27.

[7] 魏立新,郑翠红,王洪庆,等.混洗蛙跳算法的改进研究 [J].控制工程,2016, 23(2):167-172.

[8] BALA S M, MEENAKUMARI R. Optimum generation scheduling using an improved adaptive shuffled frog leaping algorithm [C]//International Conference on Cognitive Computing and Information Processing.[S.l.]：IEEE,2015:1-6.

[9] 王晨.基于混合蛙跳算法的微电网运行优化 [D].兰州：兰州理工大学,2014:19-20.

[10] 王洋,刘志珍.基于蛙跳模糊算法的Jiles Atherton铁心磁滞模型参数确定 [J].电工技术学报,2017,32(4):154-161.

[11] 王娜,高学军.一种新颖的差分混合蛙跳算法 [J].计算机系统应用,2017,26(1):196-200.

[12] 何兵,车林仙,刘初升.一种蛙跳和差分进化混合算法 [J].计算机工程与应用,2011,47(18):4-8.

[13] 葛宇，王学平，梁静. 改进的混合蛙跳算法 [J].计算机应用，2012，32(1): 234-237.

[14] 张家善,王志宏,陈应显.一种基于精英策略的改进蚁群算法及应用 [J].计算机系统应用,2012,21(10):105-108，134.

[15] 黎红玲,罗林,蒲冬梅,等.基于柯西分布的粒子群优化算法改进 [J].电子科技,2016,29(01):33-35，39.

[16] 卢宾宾,杨欢,孙华波,等.利用Minkowski距离逼近道路网络距离算法研究 [J].武汉大学学报(信息科学版),2017,42(10):1373-1380.

[17] 肖莹莹,林廷宇,李伯虎,等. 混合蛙跳算法自适应参数调整改进策略 [J].系统工程与电子技术,2016,38(8):1939-1950.