含中心孔复合材料变刚度板孔边应力解析法分析

李 阳，牛雪娟，2，潘文峰

(1.天津工业大学 机械工程学院，天津 300387；2.天津市现代机电装备技术重点实验室，天津 300387)

0 引言

炭纤维复合材料具有优异的力学性能及可设计性等优点，被广泛用于船舶、建筑、医学等领域，日益受到人们的关注。在实际应用中，由于结构或功能方面的需求，常需要在复合材料层合板上开孔或槽，这将导致在孔或槽周围产生应力集中，降低层合板的承载能力，形成潜在威胁。在发生应力集中的情况下，孔边应力大小是研究者非常关心的内容。

Nageswara等[1]根据萨文对带孔各向异性板的研究，提出一种能够计算具有对称结构的层合板及各向同性板孔边应力分布的方法，该方法还能够基于一些准则确定失效强度。Kaltackle等[2]及Sharma等[3]利用不同方法研究了单层板的不同铺层角度、不同材料特性对孔边应力的影响。William[4]研究了复合材料层合板在不同载荷方向下孔边的应力集中情况。Russo等[5]求出在单轴拉伸载荷作用下，复合材料层合板孔边的应力分布，这种计算方法包含一定的修正功能。Michele等[6]基于已有的正交各向异性弹性理论，提出能够计算槽边应力集中系数的工程公式，并利用有限元方法及已有文献验证其准确性。国内，韩小平等[7]推导出能够计算层合板孔边应力及应力集中系数的公式，根据公式分别讨论了材料弹性参数、铺层结构等因素对孔边应力集中的影响。李成等[8]用积分方法对含孔层合板进行应力分析，针对不同载荷状况对孔边的应力集中情况进行探讨。谢慈航等[9]采用各向弹性理论及保角变换法，总结出一个包含孔形参数的表达式，利用该表达式求出复合材料层合板在一定受力情况下的孔边应力，并对不同曲率孔形的应力集中系数进行了讨论。

上述国内外学者所做解析法研究以及仿真研究和实验研究，都是利用传统的直线铺放含孔复合材料层合板进行的，随着复合材料层合板制备工艺的提高，为更加充分地利用炭纤维的可设计性及其他特点，对于改变纤维角度的这种变刚度[10]层合板，国内外学者进行了相关研究。Gürdal等[11-12]采用角度沿几何轴线性变化的曲线来定义铺放参考轨迹，并采用先进的铺放技术制备了变刚度层合板；然后利用实验证明了变刚度复合材料层合板其承载能力高于直线铺放的层合板。ZHU Yingdan等[13]采用分段函数拟合最大主应力方向，通过优化目标函数获得构造参数确定铺放轨迹函数，之后进行了实验和仿真验证，但他们对变刚度复合材料层合板进行研究时，采用的都是实验和仿真的方法，没有采用解析法。

本文提出一种对变刚度板孔边应力进行解析分析的方法，根据牛雪娟等[14]提出的利用流场函数构造变刚度铺放轨迹的理论，采用合适的流场函数拟合最大主应力方向，通过优化目标函数确定构造参数，得到适用于整个变刚度板的连续的铺放轨迹函数即优化函数，基于获得的优化函数，对变刚度板孔边应力进行解析分析。

1 规划变刚度铺放轨迹

1.1 确定最大主应力方向

分析开孔复合材料直线铺放单层板在一定受力工况下的数据，获得层合板上各个单元的最大主应力方向。根据文献[15]所述，在相同的边界条件下，各向同性板与各向异性板经有限元分析后其最大主应力方向相同。分析一含中心孔复合材料0°单层板，材料为45#钢，单层板长155 mm，宽36 mm，厚2 mm，中心圆孔的直径为6 mm。利用abaqus 6.12建立模型，层合板右端在长度方向承受面内拉伸载荷10 N，边界条件为左端完全固定，原点设置在孔的中心，网格划分单元类型为C3D8R，运行后从.rpt文件中提取每个单元的S11S22S12。其中，S11为沿着x轴方向的应力，S22为沿着y轴方向的应力，S12为作用在yoz平面上沿y轴方向的剪力。利用式(1)、式(2)获得其最大主应方向，如图1所示。

(1)

可知：

(2)

1.2 设计变刚度铺放轨迹

由图1可知，在远离孔的区域最大主应力方向呈直线状分布，在孔的周围区域最大主应力方向呈余弦状分布，整个板的最大主应力方向的分布类似于圆柱绕流流线簇的分布。根据牛雪娟提出的理论，本文采用直线流与偶极流叠加来拟合最大主应力方向，通过建立目标函数获得优化的构造参数，也就获得了铺放轨迹函数。

简化后的流函数表达式为

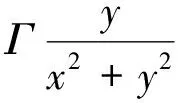
(3)

在此表达式中构造参数Γ未知，可通过如下优化目标函数获得：

(4)

此优化目标函数的中心思想为孔周围区域单元中心点处流函数的速度矢(uxi，uyi)方向与最大主应力方向(cosθi，sinθi)的夹角最小，同时考虑到这些单元中心点处的夹角在优化目标函数中的重要性其实是不同的。

式(4)中的σ1i为最大主应力代表权重就说明了不同的夹角其在优化目标函数中地位的不同。若某一点的最大主应力较大，说明该点在实际的受力情况下承受了较大载荷。因此，最好使该点的纤维方向即铺放轨迹方向与最大主应力方向一致，使纤维更有效的承受载荷，这一点在优化准则中就占有重要地位；若某一点的最大主应力较小，那么该点的纤维方向与最大主应力方向是否一致，就不是十分关心的部分，其在优化目标函数中占有地位较小。

(5)

(6)

速度矢(uxi，uyi)可通过式(6)获得，式(6)中的(xi，yi)为孔边单元的中心点坐标，利用该坐标也可获得变刚度板在x-y总坐标系下，以变刚度板中心孔的中心为原点的极角θ。最大主应力σ1i可通过式(5)获得，利用该优化目标函数能够求得构造参数Γ，最终获得该含孔单层板铺放轨迹函数。

2 含孔单合板孔边解析法分析理论基础

2.1 经典层合板理论

图2所示为单元体平衡，1-2坐标表示材料的局部坐标，x-y表示层合板总坐标，α表示从x轴到1轴的角度，逆时针方向为正。若图3单元体x轴方向平衡，可得

σx=σ1cos2α+σ2sin2α-2τ12cosαsinα

(7)

2.2 传统直线铺放含中心孔单层板孔边应力分析

含中心孔单层板承受沿x轴方向的载荷且单层板的纤维方向与载荷方向成α角，如图3所示。

对于这样的各向异性板，已有学者[2]给出求其孔边环向应力的解析式，如式(8)所示。

(8)

其中，γ1、γ2可由式(9)给出：

(9)

式中E1、E2、G12、ν12为材料的弹性常数。

接下来，利用求得的孔边环向应力σθα可求出在孔边不同极角θ处纤维方向的应力σ1，垂直于纤维方向的应力σ2以及剪应力τ12由式(10)[2]给出：

(10)

2.3 曲线铺放含中心孔单层板孔边应力分析

通过图1可知，在孔周围区域及远离孔区域最大主应力的方向，可预计利用优化函数获得的铺放轨迹大致形状如图4所示。下面对曲线铺放含中心孔单层板孔边应力分析，将利用图4进行说明。

图4中，1-2坐标的1轴方向为铺放轨迹在该点的切线方向即纤维的铺放方向，2轴方向为垂直于切线方向。α表示切线与x轴之间的夹角，θ表示该点孔边极角。α可由式(11)求出：

(11)

因为载荷施加在x轴方向，所以本文主要考察载荷方向的应力σx。先利用式(6)、式(8)、式(9)、式(11)求出孔边不同极角θ处的应力σθαi，再利用式(7)、式(10)求出σθαi沿x轴方向的分力σxi。

3 算例分析及有限元验证

3.1 算例分析

本文所用算例材料为AS4/9973，弹性常数E1=130 MPa，E2=9.24 MPa，G12=5.24 MPa，ν12=0.36几何模型，网格类型，载荷大小，边界条件等均与本文开头时所用各向同性模型相同。利用优化目标函数即式(4)，获得该模型的流函数的构造参数Γ=-5.87，离散获得的铺放轨迹函数，相邻两条等流线间的数值差为1.5，利用MatLab绘制铺放轨迹，如图5所示。利用式(6)、式(11)求得变刚度板孔边不同极角θ处铺放轨迹切线的角度，即纤维铺放角度α，如图6所示。从图6可看出，在θ约为90°、270°处，α约为0°，与最大主应力方向近乎相同，可预计其孔边应力σx将会下降。

利用在本文提出的方法，计算后可获得变刚度板孔边不同极角θ处沿x轴方向的应力σx，如图7所示。红线表示0°板孔边不同极角处的σx，黑线表示变刚度板孔边不同极角θ处的σx，从图7可看出，在θ约为90°、270°处，变刚度板的σx比0°板的σx下降11.90%，传统直线铺放单层板的应力集中得到较大改善。为更准确地说明改善情况，在表1中列出了变刚度板及0°板的极角θ在90°及270°附近角度处的σx。

极角θ/(°)变刚度板/MPa0°板/MPa76．513．223614．267585．521．614224．534894．521．368124．5348103．513．146514．2675256．513．223614．2675265．521．621324．5348274．521．334224．5348283．513．146514．2675

从图7中也可看出，变刚度板孔边环向其他角度θ处的σx要比0°板的大。分析其原因，在于变刚度板实现了应变的转移，使原本集中在垂直受力方向的应变转移到其他孔边位置，同时使材料更有效地承受载荷。

3.2 有限元验证

利用式(6)、式(11)获得铺放轨迹在每个单元中心点处切线的角度，然后利用MatLab编程，再用生成的文件更改在3.1节中由有限元模型获得的.INP文件，赋予每个单元纤维的铺放角度，即2.1节中所说的α，由此获得变刚度模型。将得到的变刚度模型重新导入有限元软件Abaqus 6.12，提取运行后变刚度模型孔边不同极角处的σx，并将其与3.1节中利用解析法获得的σx进行对比，如图8所示。红线表示利用有限元方法得到的σx，黑线表示利用解析法得到的σx。经分析可知，该解析法的最大误差是应力集中处的误差，为5.63%。

4 结论

(1)利用流场函数构造变刚度板的铺放轨迹，建立起变刚度板力学解析分析与变刚度铺放轨迹设计间的桥梁，使得采用解析法分析变刚度板孔边应力能够实现。

(2)观察利用解析法及有限元法得到的应力图，发现二者的趋势基本相同，发生应力集中的位置一样，最大误差是应力集中处的误差。解析法及有限元法的最大误差为5.63%。通过对比变刚度板及0°板孔边应力峰值，可知变刚度板应力σx的峰值比0°板的应力峰值σx下降11.90%。

(3)通过本文分析可知，若边界条件、受力工况、几何模型等条件不同，将导致其最大主应力方向不同，其中载荷施加的方式和位置是影响最大主应力方向的主要因素。这时需根据实际情况采用合适的流场函数拟合最大主应力方向，利用优化目标函数获得优化函数。

[1] Nageswara D K Rao,Ramesh M Babu,Raja K Narender reddy,et al.Stress around square and rectangular cutouts in symmetric laminates[J].Composite Structures,2010,92(12):2845-2859.

[2] Yasar M Kaltackle,Arslan H M.Stress concentions of symmetrically laminated composite plates containing circular hole[J].Iranian Journal of science & Technology Transaction B,Engineering,2006,30(B4):447-460.

[3] Dharmendra S.Sharma,Nirav P Patel,Reena R Trivedi.Opti-mum design of laminates containing an elliptical hole[J].International Journal of Mechanical Sciences,2014,85(8):76-87.

[4] William L Ko.Stress concentration around a small circular hole in the HIMAT composite plate[R].California,NASA TM 86038,1985:1-16.

[5] Russo A,Zuccarello B.An accurate method to predict the stress concentration laminates with a circular hole under tensile loading[J].Mechanic of Composite Materials,2007,43(4):59-376.

[6] Michele Zappalorto,Paolo Andrea Carraro.An engineering formula for the stress concentration factor of orthotropic composite plates[J].Composite Part B:Engineering,2015,68(6):51-58.

[7] 韩小平,郭章新,朱西平,等.含孔复合材料层合板孔边的应力集中[J].复合材料学报,2009,26(1):168-173.

HAN Xiaoping,GUO Zhangxin,ZHU Xiping,et al.Stress distribution near the opening and stress concentration for composite laminates with acircular opening[J].Acta Materiae Compositae Sinica,2009,26(1):168-173.

[8] 李成,郑艳萍,王迎佳.积分方程求解复合材料开口板的应力分布[J].玻璃钢/复合材料,2007,34(1):9-12.

LI Cheng,ZHENG Yanping,WANG Yingjia.Stress analysis of composite plate with holes by integral tunction[J].Fiber Reinforced Plastics/Composites,2007,34(1):9-12.

[9] 谢慈航,薛璞.含孔复合材料层合板的孔边应力分析及孔形优化[J].陕西师范大学学报(自然版),2014,42(4):27-32.

XIE Cihang,XUE Pu.Optimization and analysis of stress concentration in composite laminates with different cutouts[J].Journal of Shaanxi Normal University(Natural Scienc Edition),2014,42(4):27-32.

[10] Gürdal Z,Olmedo R.In-plane response of laminates with spatially varying fibre orientations:Variable stiffness concept[J].AIAA Journal,1993,31(4):751-758.

[11] Wu K,Gürdal Z.Thermal testing of tow-placed,variable stiffness panels[C]//Proceedings of the AIAA/ASME/ ASCE/AHS/ASC 42nd Structures,Structural Dynamics and Materials Conference,Seattle,WA,AIAA 2001:1190-1212.

[12] Wu K,Gürdal Z,Starnes Jr J.Structural response of compression-loaded,tow-placed,variable stiffness panels[C]//Proceedings of the AIAA/ASME/ASCE/ AHS/ASC 43rd Structures,Structural Dynamics and Materials Conference.Denver,CO,AIAA 2002:1512-1535.

[13] ZHU Yangdan,LIU Jiancai,LIU Dong,et al.Fiber path optimization based on a family of curves in composite laminate with a center hole[J].Composites Part B:Engineering,2017,111(2):91-102.

[14] 牛雪娟,杨涛,杜宇.基于流场函数的变刚度层合板铺放设计[J].固体火箭技术,2014,37(6):848-855.

Niu Xuejuan,Yang Tao,Du Yu.Path planning of variable stiffness laminates based on the flow field function[J].Journal of Solid Rocket Technology,2014,37(6):848-855.

[15] Tosh M W,Kelly D W.Fiber steering for a composite C-beam[J].Composite Structures,2001,53(2):133-141.