软酉空间及其运算性质

刘用麟，吴成达

（武夷学院 数学与计算机学院， 福建 武夷山 354300）

由于客观世界中或客观世界在向人脑反映的过程中存在着大量的不精确、不完全或不完全可靠的信息（统称为不确定信息）,因而，在现实社会中需要处理大量的不确定性信息，经典的数学方法不能有效地处理.目前有一些理论，如概率理论，模糊集理论和粗糙集理论被用来处理不确定性事物，但这些理论都有自己的困难和问题.Molodtsov[1]认为原因之一可能是这些理论的参数工具不足.为了克服这些困难，1999年Molodtsov引进了软集的概念作为一种新的处理不确定性的数学工具，他同时指出了软集的若干可能应用方向.软集理论提出后，经过一些学者的扩展研究，取得了较大进展.Maji等[2]应用软集理论于决策分析，Maji等[3]还研究了软集理论的运算.随后,Ali等[4]指出了文[3]中所提出的交、并运算的一些问题,并给出了新的运算.Chen等[5]提出了参数约简的一个新定义，并将这个定义与粗糙集理论中相关概念属性约简的进行了比较.近年来，Aktas等[6]定义了软群并给出了相关的性质，将软集理论应用到群结构上去.从此，一些学者成功地将软集合理论应用到各类代数系统上,如Feng等[7]提出了软半环，Zhan等[8]提出了软BL代数，Acar等[9]提出了软环，Akram等[10-11]提出了软李代数、软K-代数等概念.本文作者也对软代数理论作了一些研究，提出了软剩余格、软结合BCI-代数等[12-14]。已经证明软代数具有与经典代数不一样的性质。

本文将软集合理论应用到酉空间中.首先给出酉空间和软集合理论的相关知识;再对软酉空间进行了合理的定义,给出具体的例子来证明软酉空间的存在性;接着研究软酉空间的运算性质,给出软酉空间的扩展交、限制交和限制差分;最后研究软酉空间的同态性质。

1 预备知识

1.1 欧几里得空间的定义及性质

定义1.1.1[15]令V是实数域R上一线性空间,在V上定义一个二元实函数,称为内积,记成（α,β）,它具有以下性质：

1、（α,β）=（β,α）;

2、（kα,β）=k（α,β）;

3、（α+β，γ）=（α，γ）+（β，γ）;

4、（α，α）≥0,当且仅当 α=0 时（α，α）=0.

这里α，β，γ是V中任意向量,k是任意实数，称这样的线性空间V为欧几里得空间。

定理1.1.1[15]若V1,V2是欧式空间V的两个子空间,那么它们的交V1∩V1也是V的子空间.

1.2 酉空间的定义及性质

欧式空间是专门对实数域上的线性空间而讨论的,因此,酉空间就是一种欧式空间.

定义1.2.1[15]设V是复数域上的线性空间,在V上定义了一个二元复函数,称作内积,记成（α,β）,它具有以下性质：

2、（kα,β）=k（α,β）;

3、（α+β，γ）=（α，γ）+（β，γ）;

4、（α，α）是非负实数,且（α，α）=0 当且仅当 α=0.这里α,β，γ是γ中任意向量,k是任意复数,这样的线性空间V称为酉空间.

性质1.2.1[15]由内积的定义可得到以下性质：

2、（α，β+γ）=（α，β）+（α，γ）;

4、向量 α，β,当（α，β）=0 时称为正交或互相垂直.

定义1.2.2[15]设W是酉空间V的一个非空子集,若对于V中的加法及复数域C与V的纯量乘法构成复数域C上的一个线性空间,则称W为V的酉子空间.

1.3 软集合理论相关定义与基本运算

定义1.3.1[1]设U是一个论域,E是参数集,U⊂E,P（U)是 U 的幂集.若 F 是 A 到P（U)的映射,则称（F,A）为U上的一个软集合.

定义1.3.2[4]设U的两个软集合分别是（F，A）和（G,B）,定义为（H,C）这两个软集合的扩展交,此时 C=A∪B,则

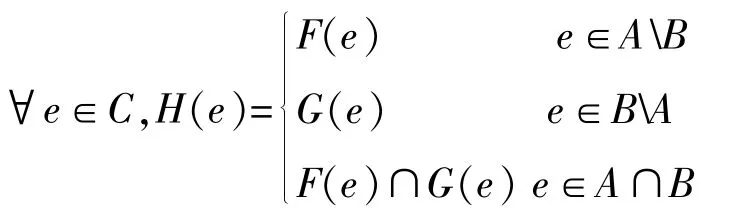
记为（F,A）∩E（G,B）=（H,C）.

定义1.3.3[4]设U的两个软集合分别是（F,A）和（G,B）,A∩B≠φ

1、此时可对这两个软集合的限制交定义为软集合（H,C）,即：C=A∩B,∀e∈C，H（e）=F（e）∩G（e）记为（F,A）∩△（G,B）=（H,C）

2、此时可对这两个软集合的限制并定义为软集合（H,C）,即 C=A∩B,∀e∈C，H（e）=F（e）∩G（e）.记为（F,A）∩R（G,B）=（H,C）

3、此时可对这两个软集合的限制差定义为软集合（H,C）,即 C=A ∩B,∀e∈C，H（e）=F（e）G（e）,记为（F,A）∩D（G,B）=（H,C）

定义1.3.4[4]设U的两个软集合分别是（F,A）和（G,B）,若满足以下条件

1、A⊂B；

2、∀x∈A，F（x）⊂H（x）.

则称（F,A）为（G,B）的软子集，记作（F,A）⊂（G,B）.

2 软酉空间

2.1 软酉空间的定义

为了便于说明,在这里令V是一个酉空间,A是一个非空集合.

定义2.1.1 设（F,A）是酉空间V上的一个软集合,若∀x∈A，F（x）,是 V 上的一个酉子空间,则称（F,A）为V上的软酉空间.

推论2.1.1 设（F,A）和（G，B）是酉空间上的两个软酉空间,如果满足下列两个条件：

1、B⊂A;

2、∀x∈B，G（x）⊂F（x）.

则称（G,B）是（F,A）的软酉子空间,记为（F,A）≾（G,B）.

定义2.1.2 设（F,A）和（G,B）是 V 上的两个软酉空间,当 G=F 时,仅需满足条件：B⊂A,则（G,B）是（F,A）的软酉子空间.

2.2 软酉空间的例子

例2.2.1 在线性空间 Cn中,对于向量 α=（α1，α2，…，αn）,β=（b1，b2，…，bn）,定义内积,则Cn就成为一个酉空间.取S=,易证 S 是 Cn的酉子空间.令 A=｛0,1｝,定义

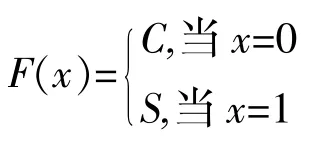
则（F,A）为 Cn上的软集合.又 F（0）=Cn,F（1）=S皆是 Cn的酉子空间,所以（F,A）为Cn上的软酉空间.

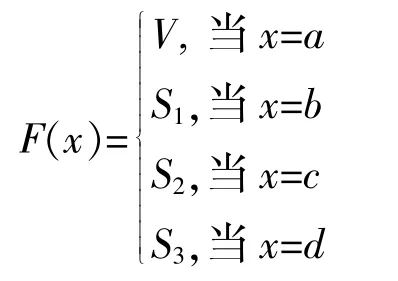
于是 F（a）=V，F（b）=S1，F（c）=S2，F（d）=S3， 都是 V 的酉子空间，所以（F，A）为｝上的软酉空间.

3 软酉空间的性质

3.1 软酉空间的扩展交

引理3.1.1 若A,B均为酉空间X的酉子空间,则A∩B也是X的酉子空间.

证明：首先,根据0∈A,0∈B可知 0∈A∩B,因此A∩B 是非空的.其次,若 α,β∈A∩B,即 α,β∈A,且 α,β∈B,则 α+β∈A,α+β∈B,于是 α+β∈A∩B.对 α∈A∩B,K∈C,即 α∈A,α,∈B,那么 kα∈A,kα∈B,因此 kα∈A∩B,所以A∩B也是X的酉子空间.

定理3.1.1 如果（F1，A1）和（F2，A2）是酉空间 X 上的两个软酉空间,则（F1，A1）∩E（F2，A2）也是酉空间 X上的软酉空间.

证明：令（F，A）=（F1，A1）∩E（F2，A2）,其中 A=A1∪A2，∀x∈A

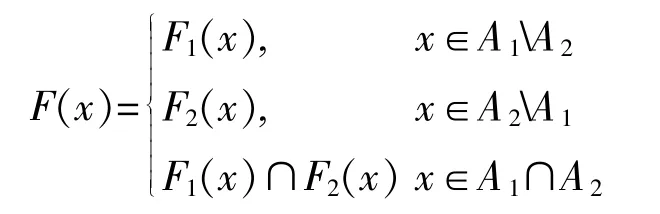
因为（F1，A1）和（F2，A2）都是酉空间 X 上的软酉空间,对∀x∈A,则x∈A1A2或 x∈A2A1或 x∈A1∩A2三者必然成立一个,若 x∈A2A1或 x∈A1A2则 F（x）=F1（x）或 F2（x）,均为 X 的酉子空间. 若 x∈A1∩A2,则 F（x）=F1（x）∩F2（x）,由引理 3.1.1,F（x）也为 X 的酉子空间.因此是（F，A）是X上的软酉空间.

3.2 软酉空间的限制交

定理3.2.1 如果（F1，A1）和（F2，A2）都是酉空间 X上的软酉空间,且 A1∩A2≠φ,则（F1，A1）∩△（F2，A2）也是X上的软酉空间.

证明：令（F，A）=（F1，A1）∩△（F2，A2）,其中 A=A1∩A2且对∀x∈A，F（x）=F1（x）∩F2（x）. 由于（F1，A1）和（F2，A2）都是 X 上的软酉空间,所以对∀x∈A1,有 F1（x）是 X 上的酉子空间;同理可得,∀x∈A2,有 F2（x）是 X上的酉子空间,因此,对∀x∈A,有F（x）是 X 上的酉子空间,从而（F1，A1）∩△（F2，A2）是 X 上的软酉空间.

3.3 软酉空间的限制差分

定理3.3.1 如果（F1，A1）和（F2，A2）都是酉空间 X上的软酉空间,且 A1∩A2≠φ,则（F1，A1）∩D（F2，A2）一定不是酉空间X上的软酉空间.

证明：令（F，A）=（F1，A1）∩D（F2，A2）,其中 A=A1∩A2且对∀x∈A，F（x）=F1（x）F2（x）.由已知,对∀x∈A,F1（x），F2（x）为酉空间 X 的酉子空间,所以 0∈F1（x）,0∈F2（x）,故 0∉F（x）.于是，F（x）不是酉空间 X 上的酉子空间,故（F1，A1）∩D（F2，A2）一定不是酉空间 X 上的软酉空间.

3.4 软酉空间的同态性质

定义3.4.1 设X和Y是复数域C上两个酉空间,f：A→B是一个映射,若满足：

1、∀α,β∈A,有 f（α+β）=f（α）+f（β）,

2、∀k∈C，α∈A,有 f（kα）=kf（α）,

则称f是酉空间A到B的一个同态映射.若f是满射,则称f是酉空间A到B的一个满同态；若f是单射,则称f是酉空间A到B的一个单同态；若f是双射,称f是酉空间A到B的一个同构.

引理3.4.1 设X,Y是两个酉空间,如果f：X→Y为从X到Y的酉空间同态：

1、假设X的酉子空间为M,那么Y的酉子空间就是 f（M）.

2、假设Y的酉子空间为L,那么的酉子空间就是f-1（L）.

证明：设∀y1，y2∈f（M）,在 M 中存在两个元素 x1,x2,使得 y1=f（x1）,y2=f（x2）.则 y1+y2=f（x1）+f（x2）=f（x1+x2）由M为X的酉子空间可知x1+x2∈M,从而y1+y2=f（x1+x2）∈f（M）；设∀k∈C,∀y∈f（M）,则 M 中存在 x,使得 y=f（x1）,于是 ky=kf（x）=f（kx）,由于 kx∈M,所以ky=f（kx）∈f（M）.因此 f（M）为 Y 的酉子空间.同理可证,f-1（L）为X 的酉子空间.

定理3.4.1 设X,Y是两个酉空间,如果f：X→Y为从X到Y的酉空间同态,（F，A）是上的软酉空间,则（f（F），A）是 Y 上的软酉空间.

证明：首先由（f（F），A）的定义知（f（F），A）为 Y 上的软集.由（F，A）是X上的软酉空间知,对任意的α∈A,F（α）是 X 的酉子空间,由引理 3.4.1,可知 f（F（α））为 Y的酉子空间,即对任意的 α∈A，f（F）（α）是 Y 的酉子空间,从而有（f（F），A）是 Y 上的软酉空间.

定理3.4.2 设X,Y是两个酉空间,如果f：X→Y为从X到Y的酉空间同态,（H,B）是Y上的软酉空间,则（f-1（H），B）为 X 上的软酉空间.

证明：首先由（f-1（H），B）的定义知（f-1（H），B）为 X上的软集.对任意的b∈B,由（H,B）是Y上的软酉空间知 H（b）是 Y 的酉子空间,因此由引理 3.4.1,f-1（H（b））是 X 的酉子空间,即对任意的 b∈B,f-1（H）（b）是 X 的酉子空间,从而有（f-1（H），B）为 X 上的软酉空间.

定理3.4.3 如果 f：X→Y 是一个酉空间同态,（F，A）和（H,B）是酉空间 X 上的软酉空间,（F，A）≾（H,B）,则（f（F），A）≾（f（H），B）.

证明：由（F，A）≾（H,B）可知 A⊂B,故对∀x∈A,有F（x）是 H（x）的酉子空间.又由 f是同态映射,有 f（F）（x）=f（F（x））是 f（H（x））=f（H）（x）的酉子空间,由定理3.4.1 可知（f（F），A）与（f（H），B）为 Y 上的软酉空间,再根据定义 2.1.2 可得（f（F），A）≾（f（H），B）.