4维Novikov代数的自同构
2018-03-15黄忠铣
黄忠铣
(武夷学院 数学与计算机学院,福建 武夷山 354300)
Novikov代数[1]是流体动力学的Poisson括号,Yang-Baxter方程算子及李群的左不变仿射结构等相关联.这种比较新的代数结构,其与众不同的特征是其左乘算子形成一个李代数,右乘算子是交换的.Novikov代数与李代数在数学和物理的许多分支有众多的应用.发展至今Novikov代数已获得了很多重要的成果.Zelmanov[2]指出特征0单有限维Novikov代数是一维的.徐晓平[3-4]确定了特征代数闭域上单Novikov代数的分类.白承铭等人给出了复数域上的一维和二维Novikov代数,以及相应自同构[5-6].Dietrich Burde和Willem de Graaf[7]指出了复数域上的三维和四维Novikov代数的分类.
本文讨论四维Novikov代数的自同构.取定一组特定的基,利用每一类四维的Novikov代数在此基下的特征矩阵,由Novikov代数的自同构的定义,通过计算确定这类Novikov代数的自同构的结构形式,以表格的形式给出所有的四维Novikov代数的自同构.并由此讨论几何经典-矩阵和某些相空间.
1 预备知识
定义1[5]设A是数域F上的向量空间,A上的双线性乘积(x,y)→xy
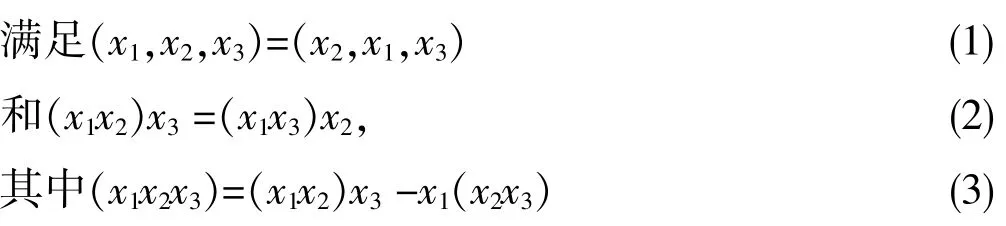
则称A为Novikov代数.如果A中的乘法只满足方程(1),则称 A为左对称代数.
定义2[6]设φ∈End(A),若φ成立
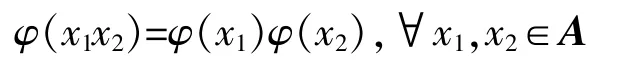
则称φ为A上的自同构.
一个Novikov代数(或一个左对称代数)A的交换子
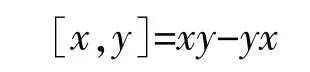
定义了一个次伴随李代数 (sub-adjacent Lie algebra)G=G(A).令 Lx=xy,Rx=yx,∀x,y∈A,则左乘算子构成一李代数,右乘算子可交换.
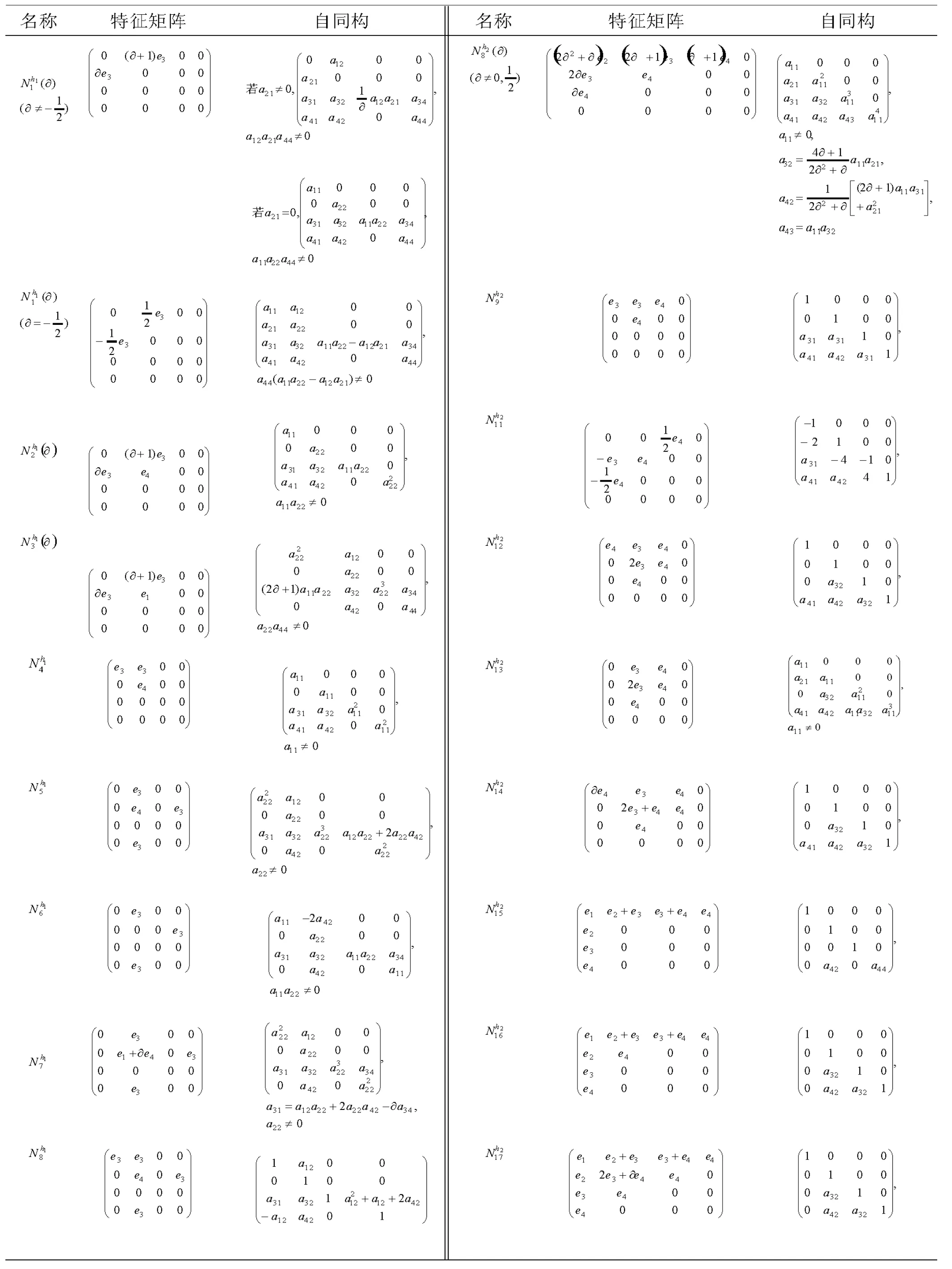
2 4维Novikov代数的自同构
设A是以e1,e2,e3,e4为基的4维Novikov代数,称矩阵

为A的特征矩阵.
应用文献[7]对4维Novikov代数的分类,可计算自同构如下.

表1 4维Novikov代数的自同构Table 1 Automorphism of the 4-dimensional Novikov algebra

续表1

续表2
续表3

续表4
定理14维Novikov代数的自同构见表1.
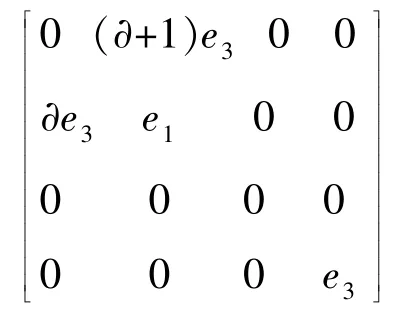
设自同构φ在基e1,e2,e3,e4下的矩阵为

由自同构的定义,首先由 φ(e1e2)=(∂+1)φ(e3),可得
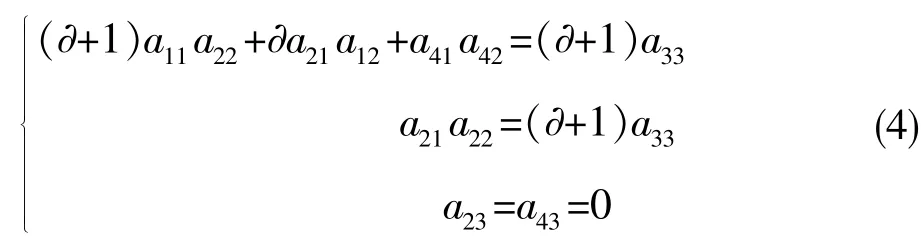
由 φ(e2e2)=φ(e1),有
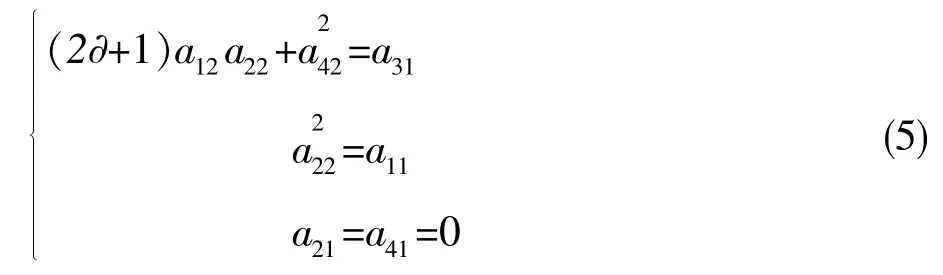
利用已得a21=a23=a41=a43=0,类似上面的过程可得
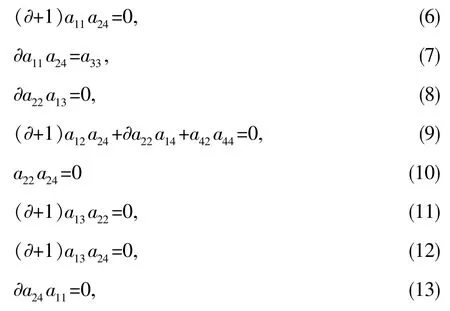
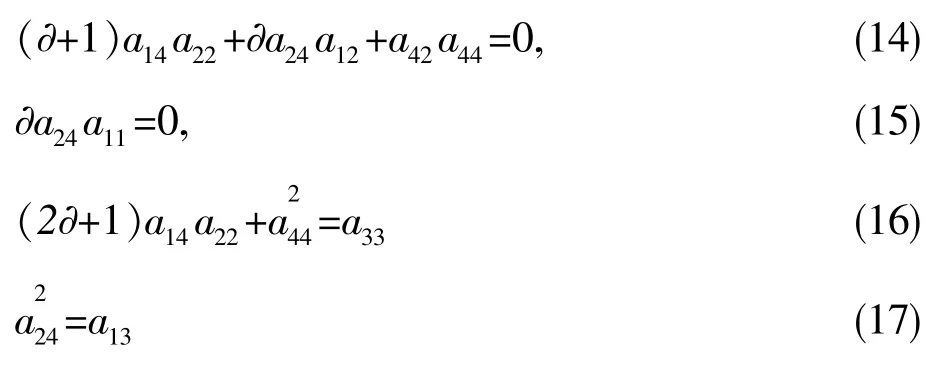
由(11)式减(8)式有 a22a13=0;由 (12)式减(15)式有a24a13=0;若 a13≠0,则 a22=a24=0,故该方阵的行列式为0,这与φ为自同构矛盾.所以a13=0,由 (17)有a24=0.从而 a21=a23=a24=0,所以 a22≠0.同理 a33≠0,由(16)a244=a33,故 a44≠0.由 (14)式减(9)式有 a14a22=0,得 a14=0,代入 (9)有 a42a44=0,得 a42=0,由(4)及 (7)有 a33=a11a22.由 (5)得 a31=(2∂+1)a12a22.因此自同构 φ 在基 e1,e2,e3,e4下的矩阵为
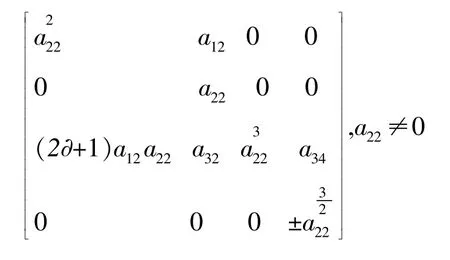
推论14维Novikov代数的自同构群的维数是大于0的有限数.
3 对应的几何经典-矩阵和相空间的等价
Novikov代数具有众多非结合代数所具有的普遍性质.任一Novikov代数的自同构也是其次-伴随李代数的自同构.Novikov代数的自同构集合构成一个李群,其李代数恰是Novikov代数的导子代数.
设G是李代数,令r∈G⊕G,r是G上经典Yang-Baxter方程的解当且仅当r在U(G)满足下式
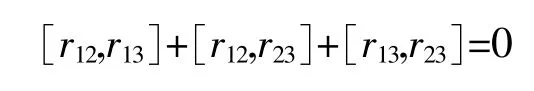
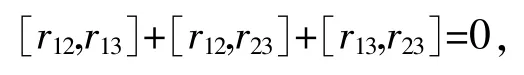
且在C[X×X]上满足幺正条件r+r21=0,则称r是几何经典r-矩阵[9].
另外,相空间[10]T*G满足如下条件:(1)T*G=G⊕G*,其中⊕表示向量空间的直和,G*是G的对偶空间;(2)T*G是满足如下定义的辛形式的李代数
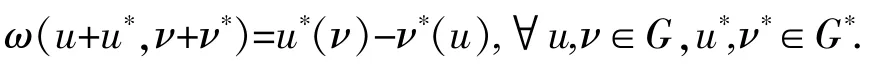
该辛形式是T*G上的一个2-循环,即
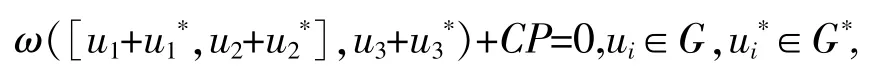
其中CP表示循环置换.
几何经典r-矩阵与相空间之间的关系有如下性质.
引理[6]令G是李代数,则如下条件等价.
(1)有一个左对称代数结构;
[u1+u1*,u2+u2*]=[u1,u2]+ρ*(u1)u2*-ρ*(u2)u1*,∀u1,u2∈G,u1*,u2*∈G*.ρ:G→gl(V)是 G 的表示,且 ρ*:G→gl(V*)是其对偶表示;
(3)有一几何经典r-矩阵.即有一李代数G',且dim G'=dimG,G是G'的表示空间,使得对在上的经典Yang-Baxter方程,在G⊕G*-G*⊕G'有反对称解;在上的李代数由下式确定
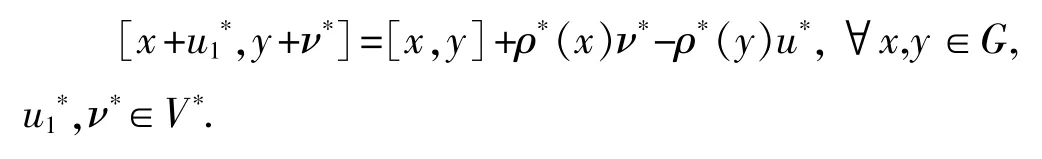
定理2 由4维Novikov代数的自同构的分类,可确定相应相空间的等价映射及几何经典r-矩阵的分类.
