一类非自治具有垂直和接触传染的传染病模型正周期解
2018-03-15许淑娴
郑 航,许淑娴,兰 玲
(1.武夷学院 数学与计算机学院,福建 武夷山 354300;2.武夷学院 机电工程学院,福建 武夷山 354300)
近年来,传染病模型是生物数学领域研究的热点之一目前已有许多工作关于传染病模型[1-5].而传染可分为垂直传染和接触 (水平)传染,Michael、Fine、Busenberg和Cook[6-9]等研究了垂直传染流行病模型,分析了其模型的稳定性等动力学行为.之后,孟新柱和陈兰荪[10],刘开源等[11]都提出在垂直传染模型中考虑脉冲和时滞因素,更加符合实际情况.另一方面,韩丽涛[12]讨论了两种群相互竞争的SIRS传染病模型的稳定性.付景超等[13]研究了具垂直传染和连续预防接种的SIRS传染病模型,并分析了其稳定性.傅金波和陈兰荪[14]提出一类垂直传染和接触传染的传染病模型,通过构造适当的Lyapunov函数来研究模型的全局稳定性条件.然而在现实环境中,很多因素是随时间发生周期性的变化,模型的系数应该是随时间变化的.因此有必要研究非自治情况,但目前非自治传染病模型的正周期解研究较少.夏米西努尔和腾志东[15]研究了一类非自治SIRS传染病模型的持久性,韩怡茹和吴事良[16]构造Lyapunov函数得出一类非自治SIRS传染病模型的全局稳定性,并应用比较原理获得模型的持久性的充分条件.陈文斌[17]应用重合度理论讨论了一类具有时滞的非自治SIR传染病模型周期解存在性的充分条件.因此受傅[14]和陈[17]的启发,本文考虑参考文[14]中的模型,将其改进为非自治新系统,研究一类非自治具有垂直和接触传染的传染病模型,模型如下:
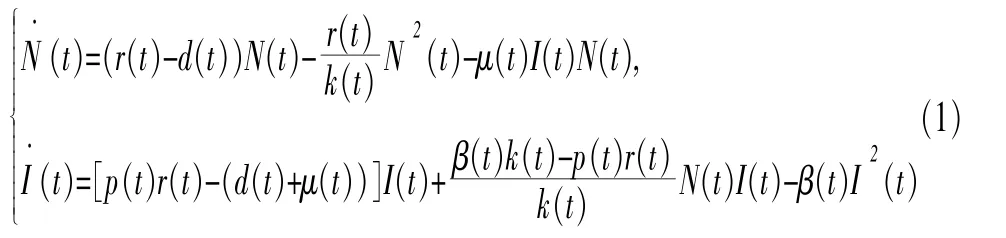
其中 N(t)为 t时刻生物种群的总数,I(t)表示为 t时刻该种群的染病类.其他参数的生物学意义见表1.

表1 参数表Table 1 Parameters
并假设所有参数均为具有w>0周期的正数,且初值 N(0)>0,I(0)>0.
1 正周期解
本文应用重合度理论中的Mawhin连续定理来证明系统(1)周期解的存在性。并记一个连续周期函数f(x)周期为 w,引入下列记号:

引理1.1(Mawhin连续定理[17]):设⊂X是一个有界开集,L:Dom L⊂X→Y是一个指标为零的Fred-holm算子,N:X→Z为上的L-紧的,假设:
(A1)对∀λ∈(0,1),Lx=λNx 的任意解满足 x∉∂Ω;
(A2) 对∀x∈Ω∩ker L,QNx≠0,且 deg{JQN,Ω∩ker L}≠0;
定理1.2如果系统(1)满足以下三个条件:
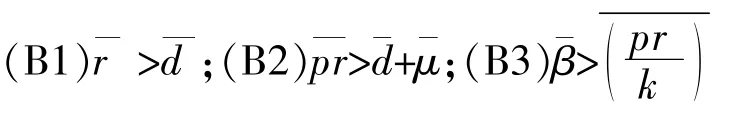
则系统(1)至少存在一个周期解.
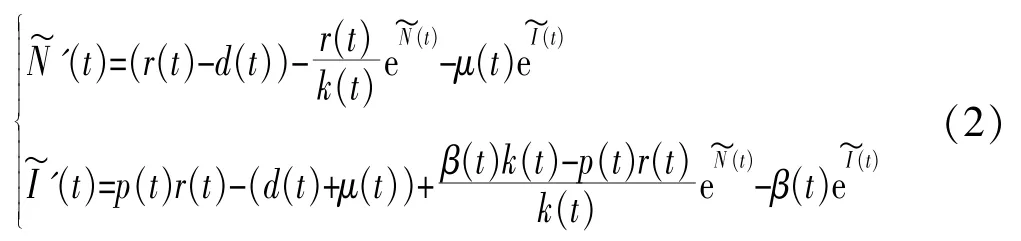
记:
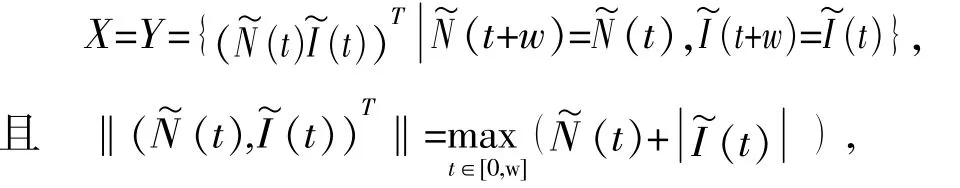
则容易证得X和Y都是Banach空间.
又定义 L:Dom l⊂X→Y
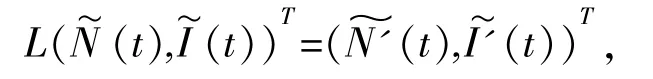
N:X→Z,进而得:
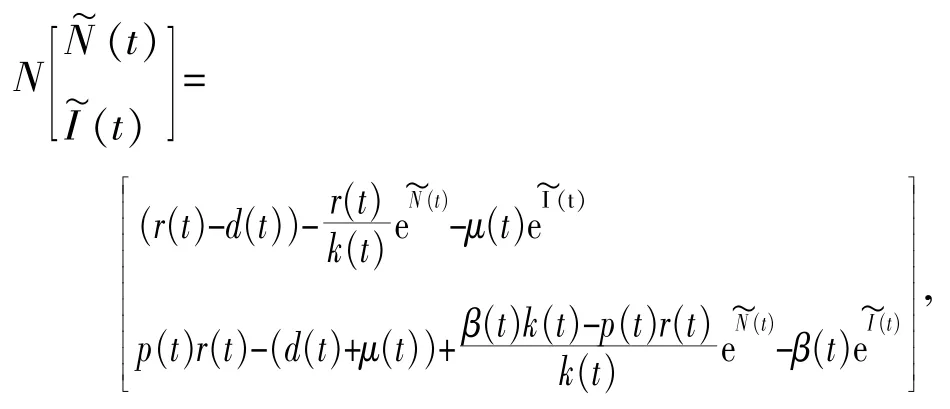
又令
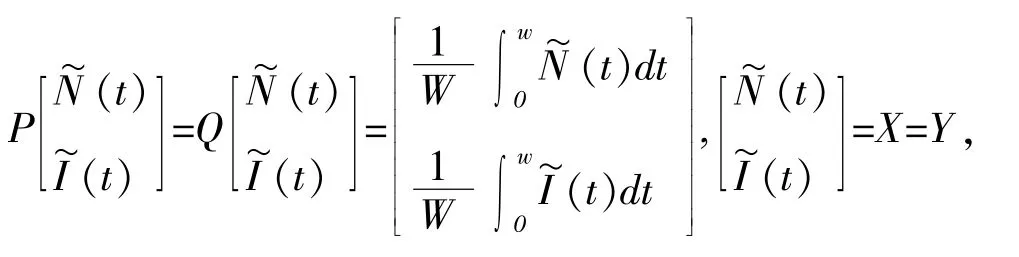
则有
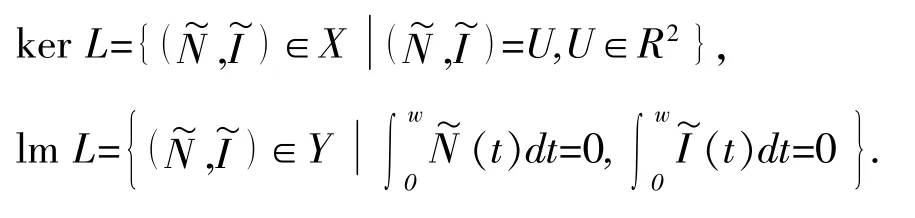
故lm L是Y中的闭子集,又由于dim ker L=codim lm L=2<+∞,故L是指标为零的Fred-holm算子,定义连续投影算子P,Q且满足:lm P=ker L,lm L=ker Q=lm(I-Q),因此 L 存在逆映射 Kp:lm L→Dom L∩ker P,具体为:
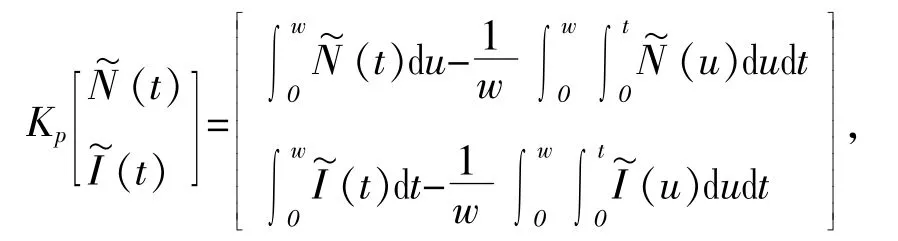
从而得:
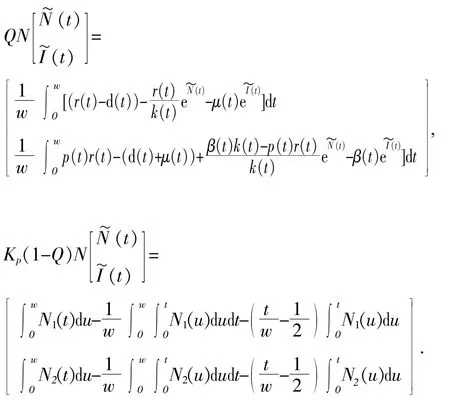
由Lebesgue收敛定理,易知QN与Kp(1-Q)N是连续的.再根据Arzela-Ascoli定理,对于X中的任意有界开集 Ω,QN()和 Kp(1-Q)N()是相对紧的.故N为的L-紧算子.对应的算子方程Lx=Nx,λ∈(0,1)有:

对(3)系统两边在[0,w]上积分得:
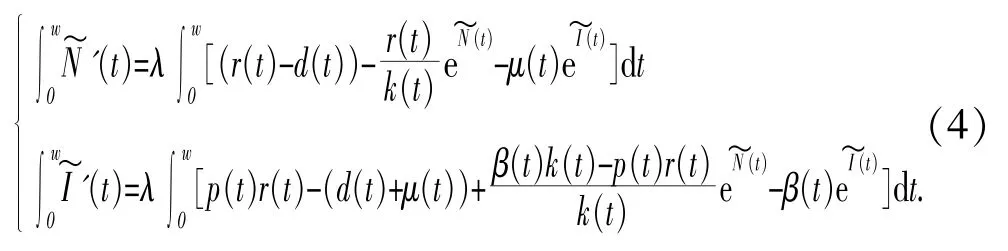
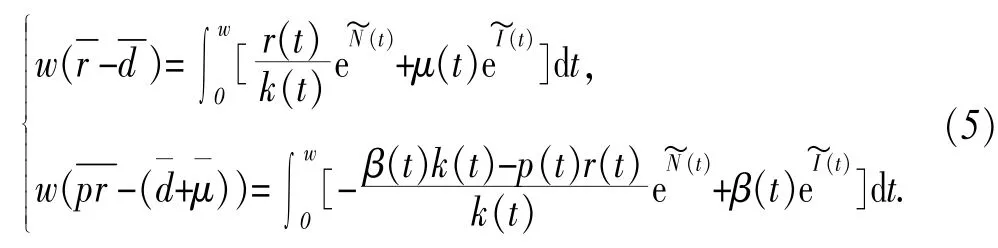
因此由(4),(5)得:
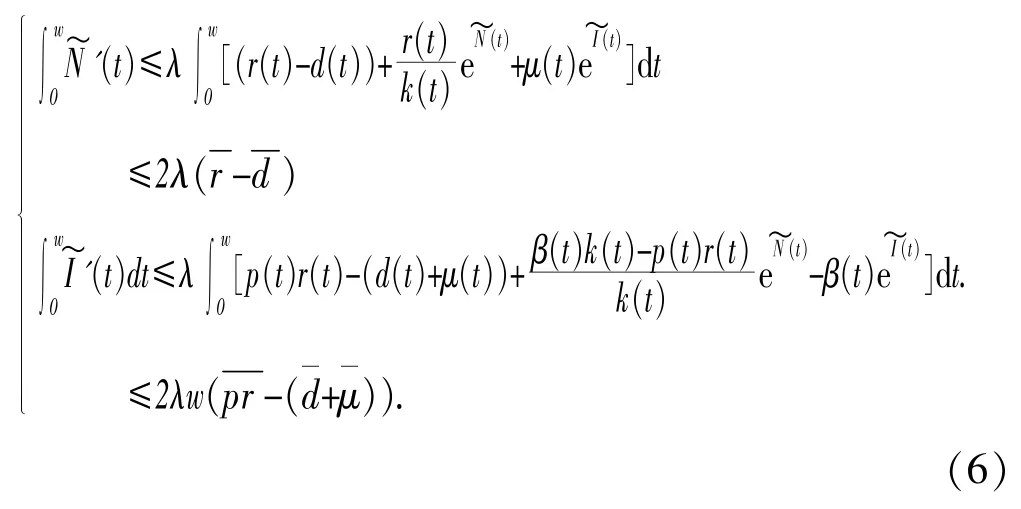
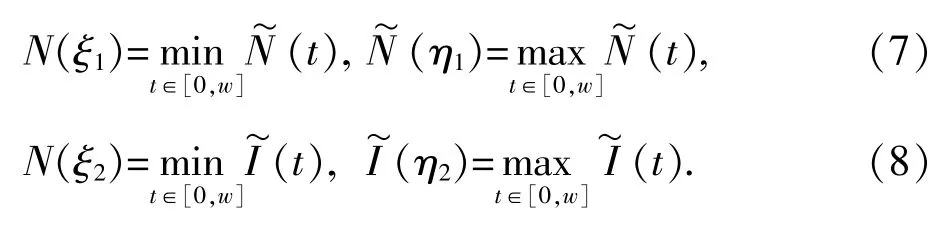
由(5)第一个方程和(7)得:
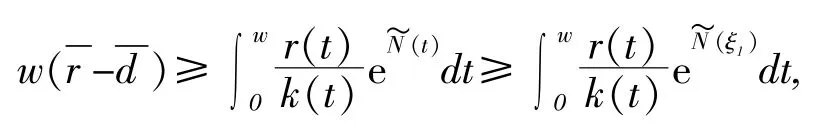
故有

再由(6),所以
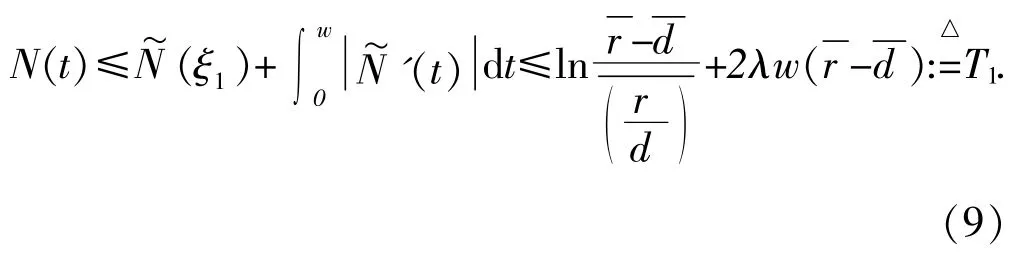
同理,由(5)第一个方程和(8)得:
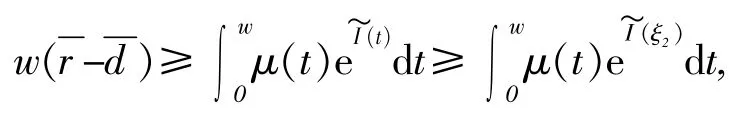
进而得
不同浓度 L-阿拉伯糖对秀丽隐杆线虫子代数目的影响结果如图 3所示,当 L-阿拉伯糖浓度为 2.5 mmol/L时,子代数目最多,相对于对照组增加了1.43%;但随着 L-阿拉伯糖浓度的增加,秀丽隐杆线虫的子代数目没有显著性的增加或减少(p<0.05,p<0.01),维持在一个较为稳定的水平,表明在现有浓度作用下,L-阿拉伯糖对秀丽隐杆线虫子代数目无显著影响。

又根据(6),因此
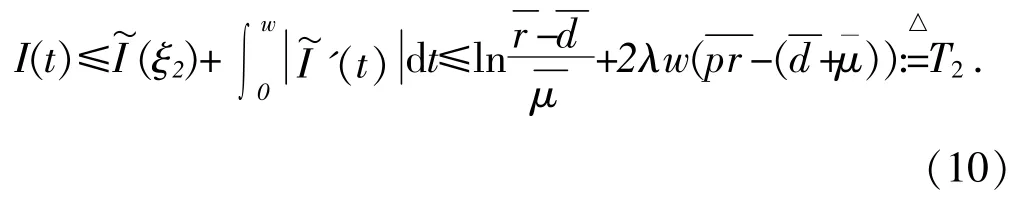
另一方面,由(5)第二个方程和(8)得:

故有
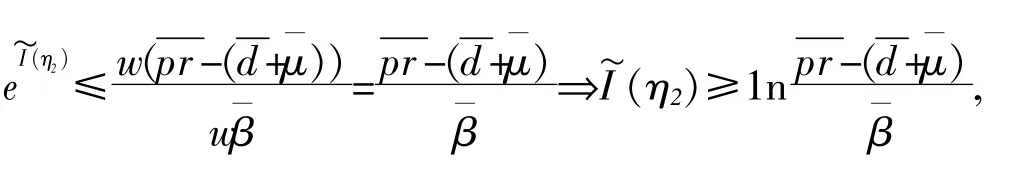
又由(6),因此
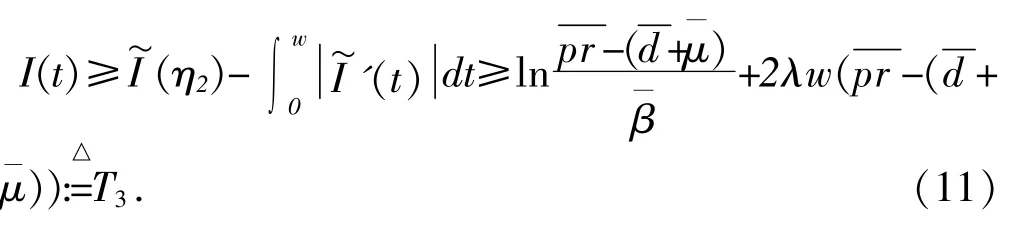
由(5)第二个方程,(7)、(8)得:

进而得

因此,再由(6)得
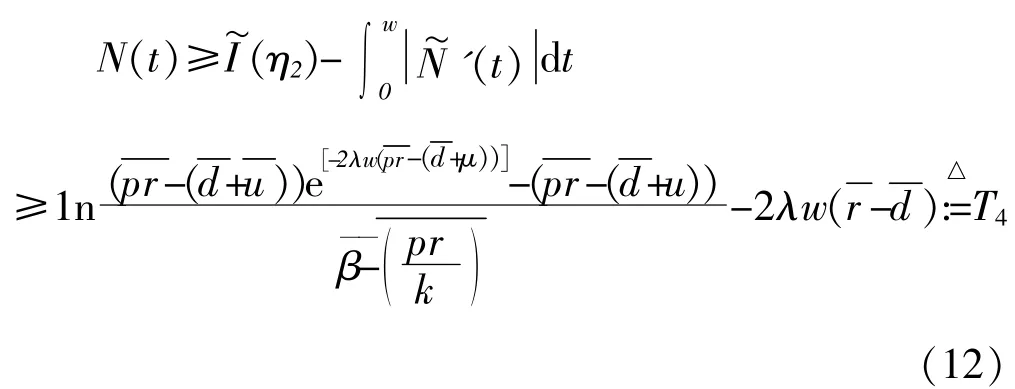
综上,由式(9)~(12)得
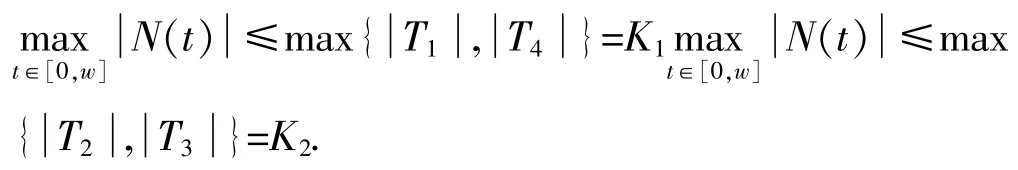
显然,K1,K2取值与 λ 无关,令,K=K1+K2+K3其中 K3>0.

为验证满足引理1.1中(A2)条件,构造代数方程:易得(13)有唯一正解(N*,I*)∈R2.当∂Ω∩ker L=∂Ω∩R2时,是R2的一个常值向量,且,则
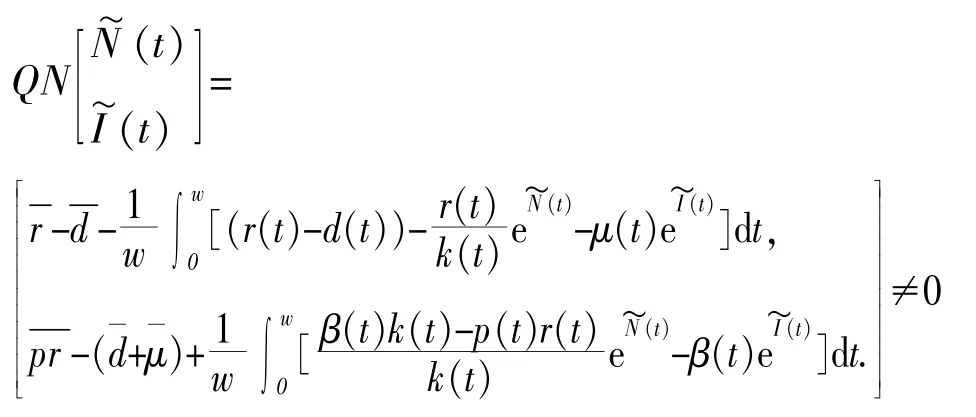
综上,J取为同构映射,故可直接计算得
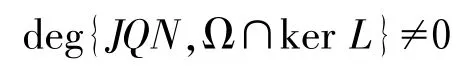
因此Ω满足引理1.1条件(A2).故Lx=Nx在Dom L∩上至少存在一个解,从而系统(1)至少存在一个周期解,定理1.2证毕.
2 数值模拟
考虑如下非自治系统:

其中,r(t)=20+sin2t,d(t)=2+cos2t,k(t)=2,μ(t)=3+cos2t,p(t)=0.58,β(t)=13-sin2t.由于,显然满足定理 1.2的(B1)-(B3)条件,系统(14)至少存在一个周期解,并用matlab数值仿真,结果见图1.
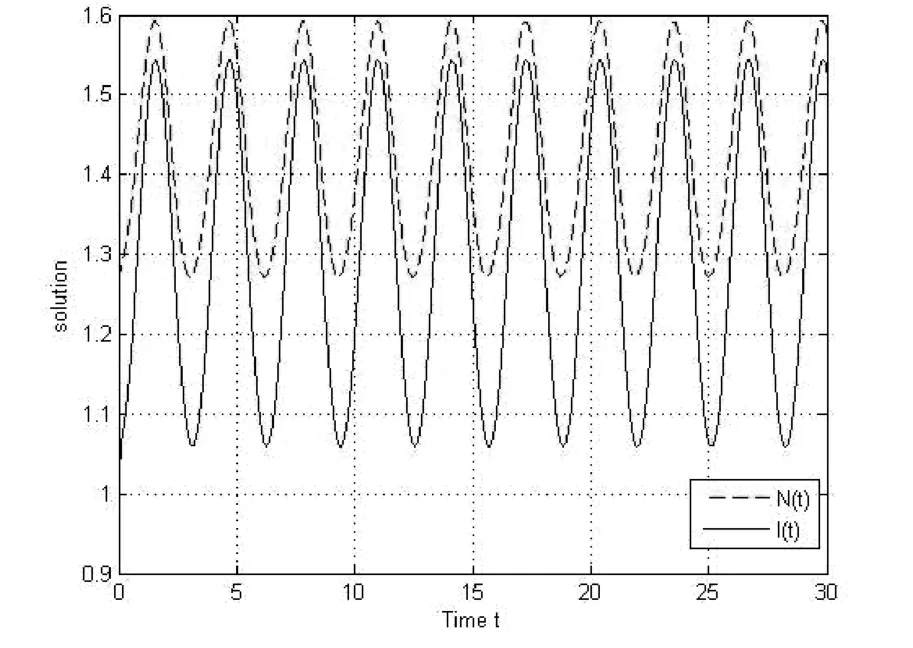
图1 周期解图(初值)Figure 1 Periodic Solution(Initial Value)
