基于6DOF模型及动网格的动静压轴承刚度阻尼数值计算*
2018-03-14王攀刘保国冯伟赵耿
王攀 刘保国 冯伟 赵耿
(河南工业大学 机电工程学院, 郑州 450001)
引言
液体动静压轴承具有回转精度高、动态刚性和阻尼减振性能好、使用寿命长等优点,在超高速精密磨削电主轴领域有着广泛的应用前景[1].电主轴系统的高速稳定性与轴承动力学特性紧密相关,因此对于轴承动态刚度和阻尼的精确计算成为研究的重点.
目前油膜轴承的数值计算模型主要有两种,一种是运用流体润滑理论并通过条件假设建立经典的雷诺方程,如Rowe等[2]基于经典雷诺方程的有限差分法,用有限扰动法得到了非线性化的动静压轴承动力特性系数.贺玉岭等[3]采用类似的方法,建立了油膜在静平衡位置做微小扰动的计算模型,进而得到动静压轴承的刚度和阻尼系数. 然而,该方法不能很好描述扩散效应、挤压效应、惯性效应、粘温效应等[4-7]对油膜轴承所造成的影响,计算误差较大.另一种是通过Navier-Stokes方程建立轴承内部三维流场模型及边界条件,并以CFD软件为求解器进行求解.该方法在涉及复杂的流动几何形状时更为有效,因此近年来得到了更多的应用.Guo等[8]用CFD程序对液体动静压轴承的静态和动态特性进行了计算,通过与标准润滑理论数值计算结果对比证明了该方法的有效性.为了反映油膜网格在外界干扰下的扭曲和变形,熊万里[9]等提出基于动网格模型的刚度阻尼计算方法,使油膜力计算结果与高速时的工况更为吻合.采用动网格法求解轴承刚度和阻尼时,首先需要准确计算轴颈在外载荷作用时的静平衡位置,以便对平衡位置施加位移扰动和速度扰动.本文基于6DOF模型计算轴颈平衡位置,采用动网格更新方法实现轴颈在该位置的扰动,通过求解Navier-Stokes方程得到轴承刚度和阻尼.
1 油膜刚度阻尼计算方法
采用6DOF模型及动网格的计算方法是在CFD软件FLUENT基础上,通过加载6DOF自定义程序,计算外载荷作用下轴颈的非线性轴心轨迹,从而得到轴颈在外载荷作用下的静平衡位置.通过嵌入UDF程序DEFINE-CG-MOTION以动网格更新方法来实现对处于静平衡位置的轴颈施加扰动;为有效抑制网格在施加扰动过程中的扭曲变形,通过嵌入UDF程序DEFINE-PROFILE来定义轴颈(油膜内壁)为旋转运动.最后通过求解Navier-Stokes方程得到轴颈扰动前后位置变化的瞬态油膜力,结合数值计算的差分方法,得到动静压轴承油膜刚度、阻尼动力特性系数.
1.1 6DOF计算模型
ANSYS FLUENT中的6 DOF模型,可以利用作用于物体的力和力矩来计算物体重心的平移和旋转运动.其在惯性坐标系下求解重心平移运动的控制方程为:
(1)
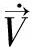
物体的旋转运动在体坐标系下的控制方程为:
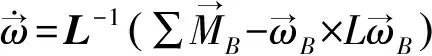
(2)
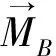
(3)
R代表变换矩阵,
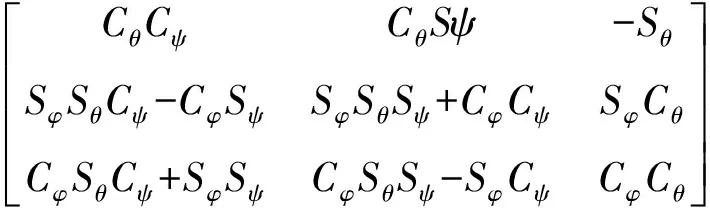
(4)
式中,Cλ=cos(λ),Sλ=sin(λ),角φ,θ,ψ分别为绕x,y,z轴旋转的欧拉角.平移速度和旋转角速度可由式(1)和(2)分别迭代计算得出,在6 DOF模型中网格位置的更新由平移速度和旋转角速度实现.
1.2 加载UDF宏的动网格更新方法
动网格方法可用来模拟流体域的形状由于边界移动而随时间产生的变化,油膜网格运动需要用光顺模型来调整变形边界区域的网格,本文选用基于弹簧的光顺模型和基于扩散的光顺模型.
(1)基于弹簧的光顺,任何两个网格节点之间的边界可以理想化为相互连接的弹簧,且边界节点处的位移将产生成比例的弹簧力,网格节点上的作用力可写为:
(5)
式中,Δxi和Δxj为相邻节点之间的位移,ni为相邻节点的数目,kij为相邻节点之间的弹簧刚度系数,其相邻节点弹簧刚度系数的定义为:
(6)
式中,kfac为弹簧常数因子需要自己设定,取值范围在0与1之间.
(2)基于扩散光顺,网格运动由扩散方程控制:
(7)
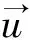
1.3 刚度阻尼差分计算模型
当轴颈受到扰动在静平衡位置偏移一微小距离时,油膜反向承载力的增量对该微小扰动距离的比值称为刚度.在分析计算时,常常把微小偏移分解为沿坐标轴x和y方向的分量,油膜反力的增量也分解成沿x和y方向的分量,分别对其进行差分计算,得四个刚度系数:
(8)
式中,ΔFdij为扰动位移引起的油膜力变化,Δx、Δy为扰动位移.用i,j表示x,y中的某一个.
当轴颈在静平衡位置获得一扰动速度时,油膜阻尼力的增量与该扰动速度的比值称为阻尼.把油膜阻尼力增量和轴颈扰动速度的增量分别分解到x轴和y轴上,可以得到四个阻尼系数:
(9)
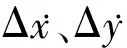
2 油膜轴承刚度阻尼数值计算
2.1 油膜模型建立及网格划分
以深浅腔液体动静压轴承为研究对象,轴承结构如图1所示,结构参数如表1所示.

图1 深浅腔动静压轴承结构图Fig.1 Structure diagram of Deep/shallow pocket hybrid bearing

表1 轴承基本结构参数Table 1 Basic structural parameters of the bearing
在Solidworks里建立油膜实体模型,如图2所示.将模型导入ANSYS ICEM CFD中,采用O型Block分块的结构化网格划分方式对油膜模型进行网格划分.考虑油膜厚度方向油膜剪切应力梯度大,沿厚度方向的网格等分为10层,网格数为100万个,划分后的网格模型如图3所示,进油孔部位及油膜厚度部位的局部放大如图4和图5所示.

图2 三维油膜实体Fig.2 Three-dimensional oil film entity
2.2 边界条件的确定
将网格文件导入FLUENT进行油膜流场数值仿真,边界条件取进油口为Pressure-inlet,供油压力为Ps;出油口为Pressure-outlet,出油口是轴承与轴颈两表面之间的微小间隙,出油口压力等于外界大气压力,其值设为0;油膜内壁面设置为旋转壁面,转速为500rad/s,其它面设置为静止壁面,油膜计算参数表2所示.

图3 油膜网格划分模型Fig.3 Model of oil film mesh

图4 油孔过渡区O型划分Fig.4 O-Shape division of oil-hole transition zone

图5 油膜厚度方向局部放大Fig.5 Partial amplification of oil film thickness direction
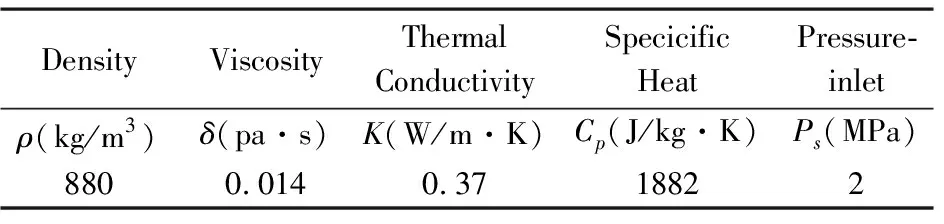
表2 油膜计算参数Table 2 Oil film Calculation parameters
2.3 动网格UDF宏程序
动静压轴承油膜内壁在主轴运转过程中受到外加载荷的作用而产生偏移,此过程属于被动型动网格计算问题,可以编写6DOF自定义程序来解决.首先需要明确模型中6个方向的自由度,动静压轴承油膜在实际运动过程中,需要限制其在轴向的窜动,以及绕三个坐标轴方向的转动.定义轴承所受外加载荷为Fx=0,Fy≠0,转轴质量为m,轴颈转向为逆时针,描述油膜内壁受外加载荷的运动示意图如图6所示.油膜内壁在外加载荷Fy的作用下做刚体运动,油膜内壁受力后向右下角移动.
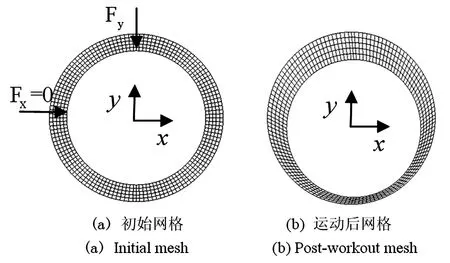
图6 油膜内壁在外载荷作用下的运动示意图Fig.6 Motion diagram of oil film inner wall under external load
通过编写UDF程序DEFINE-CG-MOTION来指定特定区域的网格运动,其方法是在每个时间步长内为动态网格区域提供线速度和角速度,FLUENT利用这些速度更新动态区域上的节点位置.
2.4 动静压油膜轴承动力特性计算流程
在6DOF程序里定义油膜内壁受力为Fx=0N,Fy=1000N.将6DOF程序加载到FLUENT求解器并作用于油膜内壁.在外载荷作用下油膜内壁网格产生偏移并稳定于一位置,此时油膜由偏心所产生的油膜反力为Fx=-0.529N,Fy=998.7N.轴颈在平衡位置一般应满足条件|Fx/Fy|<0.001,经验算满足条件.
外加载荷力作用下轴颈的轴心轨迹变化曲线如图7所示,可以看出其轴心轨迹是收敛型的,轴心由初始位置原点出发,经过一定幅度的涡动,最终平衡稳定于一点,此时油膜反力与轴颈重力和外加载荷保持平衡.
轴颈x方向和y方向位移随时间的变化如图8所示,轴颈在初始阶段受到较大幅度的震荡,随着不断的迭代计算轴颈的偏移不断减小,在计算时间t=0.05s左右,轴颈趋于稳定并在静平衡位置附近做微小幅度的涡动,其幅值在千分之一微米级,说明此系统处于稳定状态.
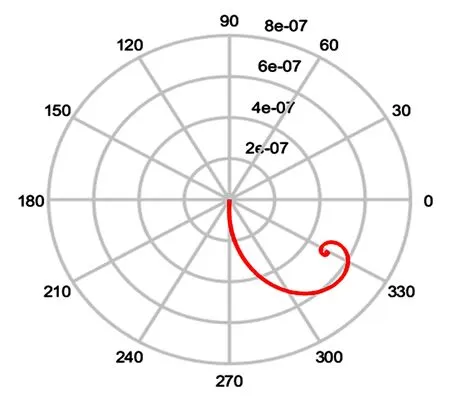
图7 外加载荷力作用下轴心轨迹变化曲线Fig.7 The change curve of axis trajectory under the action of external load force
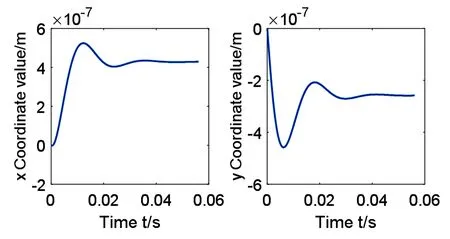
图8 x方向和y方向位移随时间t的变化Fig.8 The change of x direction and y direction displacement with time t
轴颈x方向和y方向的油膜力随时间的变化曲线如图9所示,当轴颈达到稳态的时候,油膜反力抵消了外载荷Fy的作用,轴颈处于稳态状态.
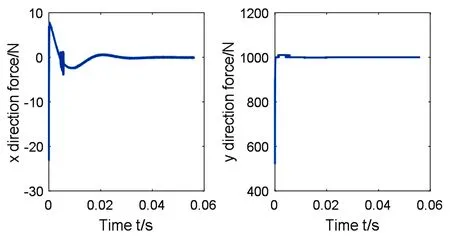
图9 x方向和y方向受力随时间t的变化Fig.9 The change of force in x direction and y direction with time t
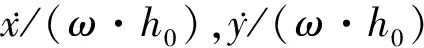
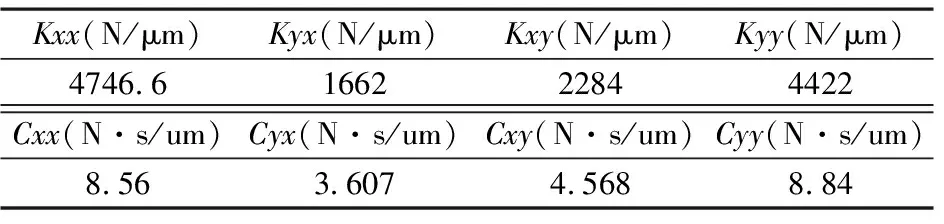
表3 油膜刚度阻尼系数Table 3 Oil film stiffness and damping coefficient
2.5 不同转速下动静压轴承刚度阻尼系数
采用上述动静压轴承刚度阻尼计算方法,对不同转速的动静压轴承刚度阻尼进行计算,得到不同转速下动静压轴承油膜的4个刚度系数和4个阻尼系数,如图10和图11所示.从图中可以看出,随着轴颈转速的增加,轴承直接刚度系数Kxx、Kyy和交叉刚度系数Kxy、Kyx绝对值逐渐增大.直接阻尼系数Cxx、Cyy和交叉阻尼系数Cyx、Cxy绝对值也逐渐增大.
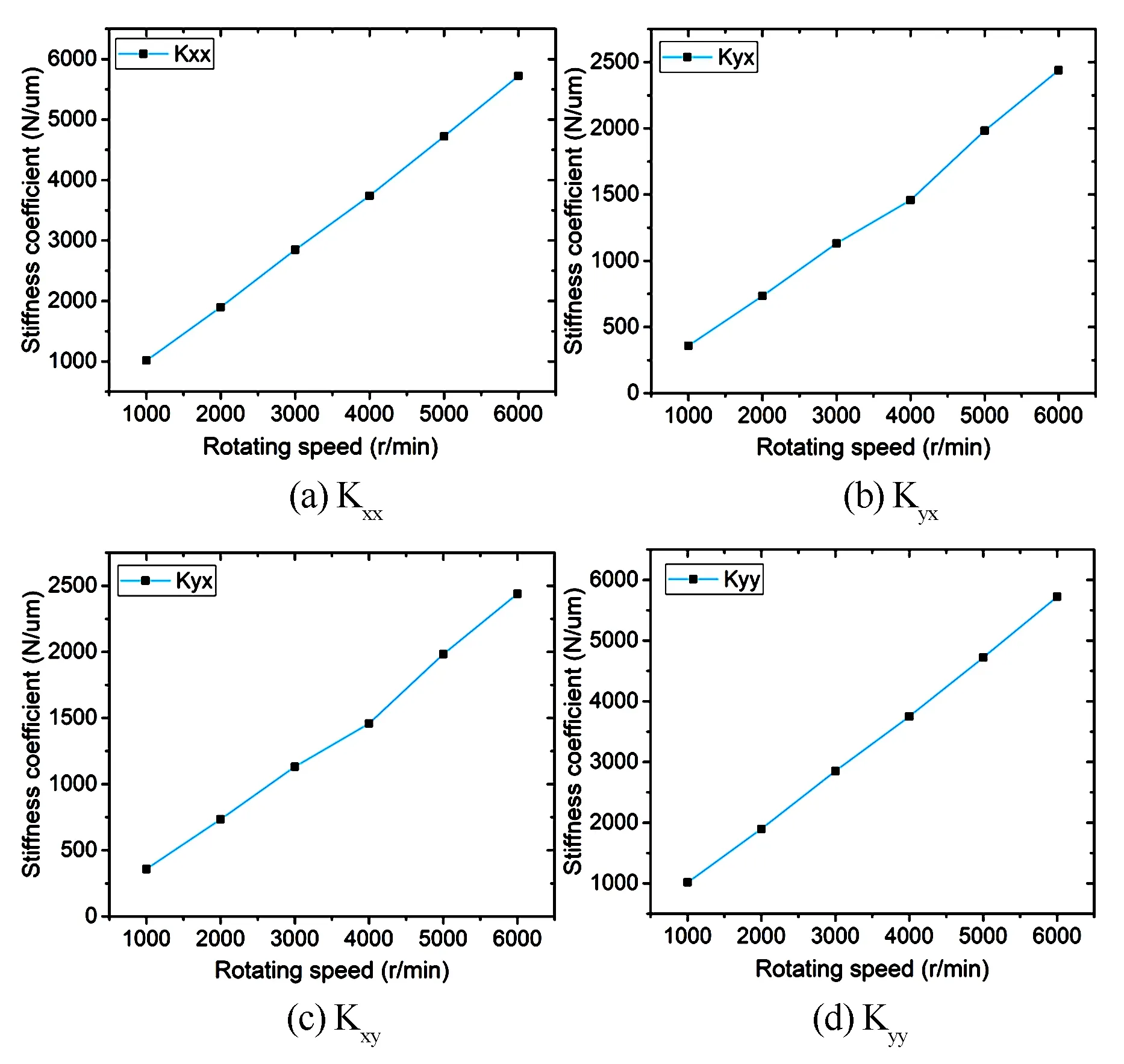
图10 各转速下油膜刚度系数Fig.10 The stiffness coefficient of oil film at each rotational speed
3 结论
本文采用6DOF模型及动网格的计算方法对具有典型结构的液体动静压轴承的刚度阻尼系数进行数值计算,通过研究分析得出以下结论:
1)采用6DOF模型可以反映油膜厚度在外载荷作用下的运动变化过程,能够更为准确地计算轴颈静平衡位置,使计算过程更符合工程实际;
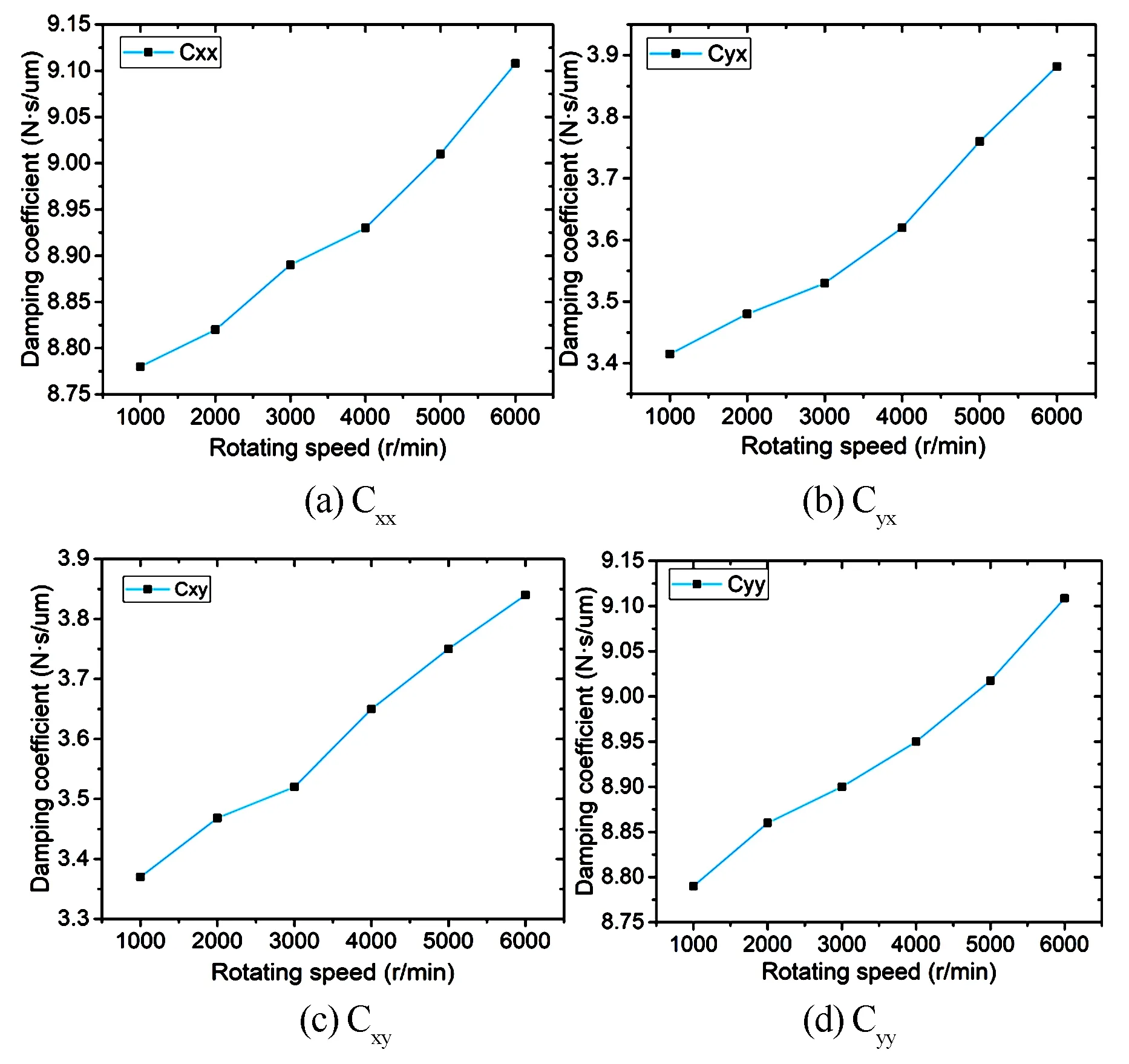
图11 各转速下油膜阻尼系数Fig.11 The damping coefficient of oil film at each rotational speed
2)利用UDF宏程序以动网格方法实现对轴颈静平衡位置的扰动,通过计算轴颈位移扰动、速度扰动前后的瞬态油膜力,利用差分法求得轴承刚度和阻尼系数;
3)分析了不同转速下轴承刚度和阻尼的变化规律,结果表明随着主轴转速的增加轴承刚度系数和阻尼系数绝对值不断增大.
