球轴承非线性动态刚度特性及其复杂共振行为研究*

董文凯 张智勇,† 芮筱亭 陈予恕 靳玉林

(1.南京理工大学 理学院,南京 210094) (2.南京理工大学 发射动力学研究所,南京 210094)(3.哈尔滨工业大学 航天学院,哈尔滨 150001) (4.四川大学 空天科学与工程学院,成都 610065)

引言

滚动轴承作为旋转机械中转子系统核心支承部件,在工业部门中广泛应用.随着国民经济的增长以及国防事业的发展,旋转机械正在向高速、重载和自动化方向发展,对轴承-转子系统的稳定性、安全性提出了更高的要求.滚动轴承内圈一般与转轴是过盈配合的,滚动体在自转的同时随着保持架在滚道绕转轴公转.在各个滚动体公转进入和离开承载区域过程中,轴承的刚度是时变的,时变刚度诱发的振动通常称为变柔度(varying compliance,VC)振动[1-3].滚动轴承的时变刚度特性是转子-轴承系统的不可避免的参激源,已经有大量研究指出滚动轴承的VC振动具有复杂的滞后共振响应特性[4-9].然而,迄今有关轴承非线性时变刚度特性对系统VC共振及其分岔行为影响的专门研究尚少.

针对滚动轴承VC振动问题,Sunnersjö[10]较早分析了考虑惯性力的线弹性圆柱滚子轴承模型,发现VC振动可以给系统带来周期运动和不规则的非周期运动.Fukata等[1]进一步研究了考虑赫兹接触非线性的经典两自由度轴承模型,指出JIS6306球轴承VC振动在轴承共振频率区间具有拍振(其中包括准周期运动行为)和类混沌(chaos-like)运动行为,并且发现在一阶临界转速附近系统存在VC亚谐振动.Rahnejat和Gohar[11]研究指出在考虑润滑的情况下钢球数量和径向游隙对深沟球轴承VC振动的影响依然显著.Mevel和Guyader[2,12]通过数值计算和实验讨论了JIS6306球轴承VC振动通向混沌的道路,发现系统存在倍周期分岔和准周期运动进入混沌的形式,其中倍周期分岔主要发生在一阶临界转速范围.Sankaravelu等[4]把打靶法与同伦延拓法相结合,发现滚动轴承VC振动响应曲线具有滞后行为. Tiwari和Gupta[3,13]研究了平衡、不平衡刚性转子-滚动轴承系统的VC振动,发现系统共振幅频响应区间具有突跳失稳和阵发性混沌振动特征.白长青、许庆余等[14]研究了深沟球轴承VC振动的稳定性,指出VC周期运动幅频响应的不稳定区间的个数随轴承径向间隙的增加而增多.崔立和王黎钦等[15]建立了一种拟动力学球轴承模型,发现轴承非线性可使支承刚性转子系统的周期运动发生突跳、倍化以及混沌振动等非线性行为.邓四二等[16]理论和实验证实轴承间隙对转子系统的支承刚度、运行稳定性有显著影响.

传统上,滚动轴承被称为滚动接触轴承[17,18],这是针对滚动体与滚道之间的接触变形关系而言的,且二者接触变形一般认为满足赫兹接触理论假设：(1)材质均质；(2)接触区域尺寸远小于接触体尺寸；(3)不考虑接触区摩擦,且作用力垂直于接触面；(4)变形属于弹性变形.接触共振是指接触非线性系统在线性等效共振频率区间内的共振特性,Nayak[20]比较早地采用谐波平衡法分析了单自由度赫兹接触系统在简谐激励下的响应特征,发现系统在接触主共振区间幅频响应曲线向左偏,即系统具有软的动力学滞后共振行为.Rigaud和Perret-Liaudet[21]明确指出只有采用接触非线性模型才可能准确地预测系统的响应特性.球轴承受载过程中,将在滚珠和滚动之间产生赫兹接触变形[19].张智勇、陈予恕等[7,8]采用谐波平衡-频时转换(HB-AFT)方法结合Floquet理论研究了球轴承VC振动的赫兹接触共振特性及其参数影响规律,发现系统具有软的滞后主共振行为,并被随后实验证实[9].

就滚动轴承-转子动力学而言,学者们更加关注滚动轴承的支承特性和时变激励特征对轴承及整个转子系统的振动特性和运动稳定性等方面的影响[19,22-24],有大量工作[25-27]对滚动轴承动态时变刚度的计算方法和影响因素进行了研究.Harris[19]明确指出由于滚珠与滚动体之间的非线性受力-变形关系,轴承支承刚度具有时变特性且与转轴转速有关,而研究球轴承动态刚度特性及其对VC振动的影响具有基础理论意义.本文将以HB-AFT方法和数值积分方法为主要分析手段,对球轴承的非线性动态刚度特性及其复杂共振行为展开研究,拟探究系统动态刚度特性与主共振区间复杂运动分岔行为的内在关联.

1 模型

在研究考虑轴承径向间隙、轴承时变刚度和赫兹接触力等非线性因素的球轴承VC振动时,采用如图1所示的2自由度深沟球轴承模型就可得较好的定性和定量的结果[3,8,12].

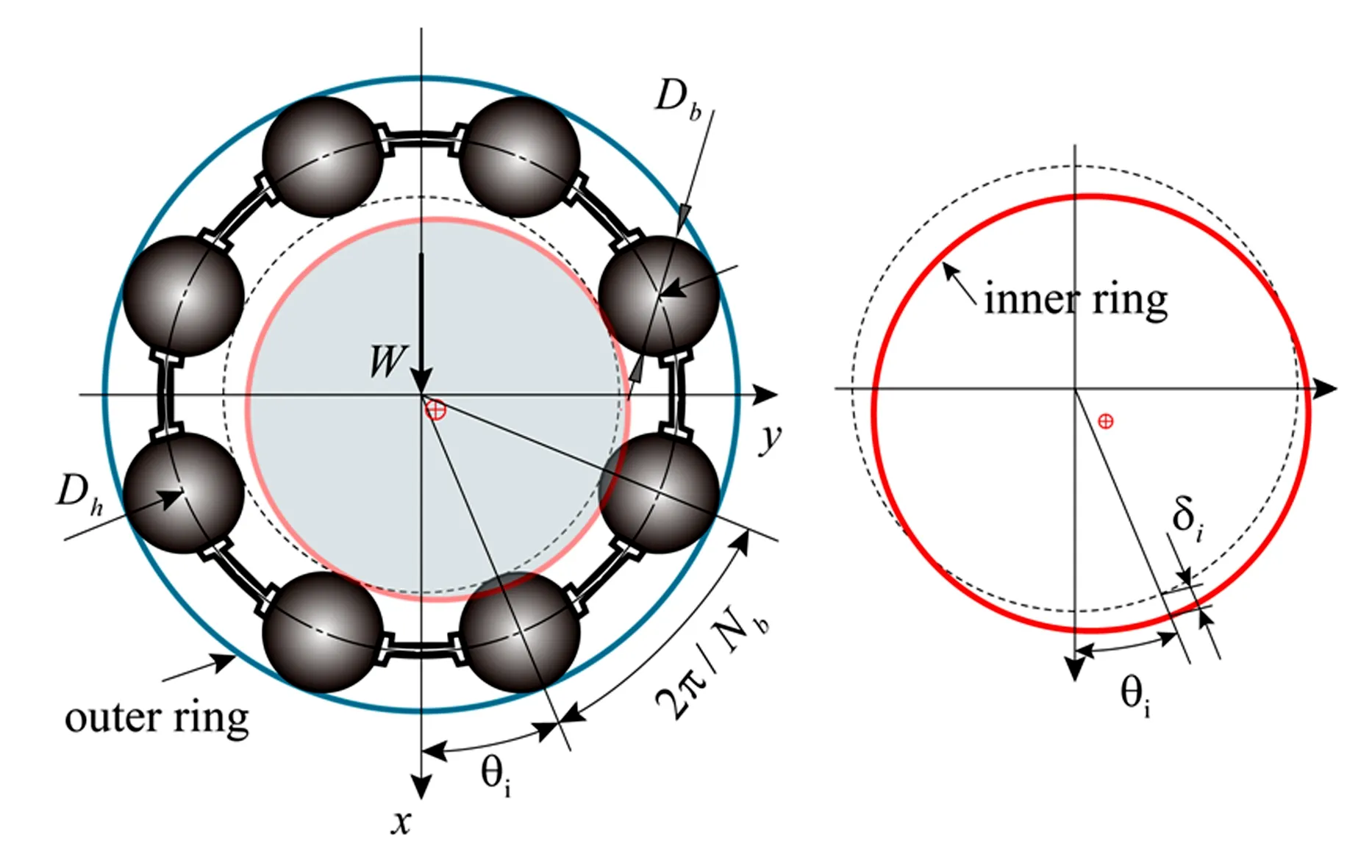
图1 经典两自由度深沟球轴承模型及其径向位移变形关系Fig.1 Classical 2-DOF deep groove ball bearings and its displacement-deformation relationship in radical direction

第i个滚动体的瞬时角位置为：

θi=2π(i-1)/Nb+Ωt

(1)

式中,Nb为滚动体个数；Ω为保持架转速(rad/s).

其中Ω与转轴转速ωs、轴承内圈半径ri以及外圈半径ro的关系为：

(2)

在小变形条件下,第i个滚动体与轴承套圈的接触变形表示为：

δi=xcosθi+ysinθi-δ0

(3)

这里2δ0为轴承的径向游隙.

对于球轴承,不考虑润滑条件下钢球与滚道之间的位移变形关系满足赫兹点接触,则轴承恢复力满足：

(4)

式中,Cb为轴承的赫兹接触刚度(N/m3/2)；G[·]为Heavisde函数.

球轴承-刚性Jeffott转子系统的运动微分方程为：

(5)

式中,m为转子系统等效质量(m)；c为轴承等效阻尼(Ns/m)；W为轴承内圈承受重力(N).

球轴承在承载后,将在滚珠和滚动之间产生赫兹接触变形,由于滚珠与滚动体之间的非线性受力-变形关系,轴承支承刚度是与系统参数相关的时变量.根据恢复力(4)式,可求得系统线性化动态刚度为[2,23]：

(6)

则球轴承的时变固有频率为：

(7)

就VC振动而言,滚珠通过频率激起的VC周期1运动是系统的基本运动形式,系统(5)式VC参激频率为：

ΩVC=Nb·Ω

(8)

则系统VC周期1运动在x方向或y方向发生参激主共振的条件为：

(9)

对于球轴承-刚性转子系统,其支承力仅在滚珠和滚道之间引起赫兹接触变形,则(9)式所表示的共振本质上是由赫兹非线性引起的参激接触主共振.

2 方法

本文采用HB-AFT方法求解系统VC周期响应,并采用Floquet理论对解的稳定性进行分析.首先,进行式(5)的位移和非线性力的谐波平衡化过程：

(10)

(11)

把式(10)、(11)代入方程(5),谐波平衡可得：

g(P,Q)=0

(12)

其中P、Q分别表示位移和非线性力谐波系数.

把Q记为已知,可采用Newton-Raphson迭代求解不动点P：

J(i)(P(i+1)-P(i))+g(i)=0

(13)

其中,迭代Jacobian矩阵：

J=dg(P,Q)/dP

=∂g(P,Q)/∂P+∂g(P,Q)/∂Q·dQ/dP

(14)

迭代过程中,采用AFT转换给出式(14)中dQ/dP的关系.然后,对所得周期解进行Floquet稳定性分析[8].

3 分析结果

对于如表1所示的JIS6306深沟球轴承-转子系统,取轴承游隙为δ0=1.0μm时,如图2所示系统在Ω=180rad/s、200rad/s和220rad/s时的动态刚度都是周期性时变的,而且与已有文献[19,27]结果一致,系统的VC特性是随转速变化的.另外,由式(7)可知,系统的动态固有频率同样随转速变化的.滚动轴承VC振动是由滚动体公转引起的一种不可避免的时变刚度参激振动,下面分析JIS6306球轴承系统随转速的全局周期响应特性.

表1 JIS6306轴承-转子系统参数Table 1 Specifications and parameters of JIS6306 ball bearing-rotor system

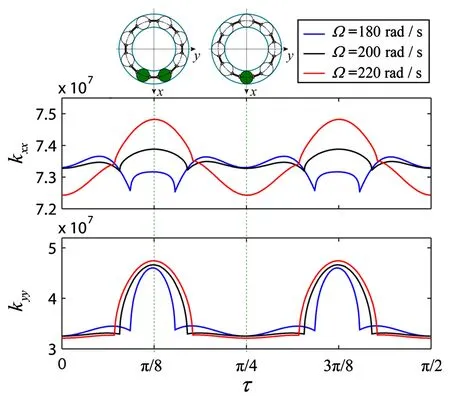
图2 当 δ0=1.0μm时,系统在Ω 取180rad/s、200rad/s和220rad/s时的动态刚度,其中τ = Ω tFig.2 For δ0 = 1.0 μm,the system dynamic stiffness when Ω takes 180 rad/s,200 rad/s and 220 rad/s,here τ = Ω t

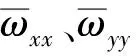
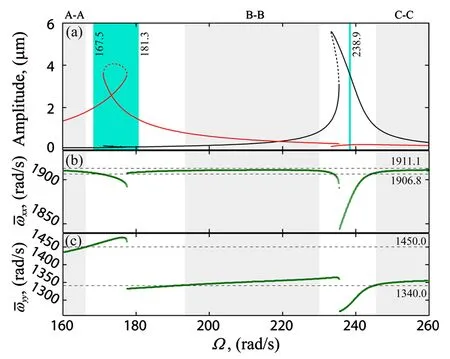
图3 当δ0 = 1.0 μm时,(a) x (黑线)、y (红线)方向稳定(实线)和不稳定(虚线)的VC周期解频响峰峰值曲线,为系统动态等效固有频率随Ω的变化值Fig.3 For δ0 = 1.0 μm,(a) stable (solid) and unstable (dashed) VC periodic frequency-response peak to peak curves, c=200 Ns/m inx (black line) and y (red line) directions respectively,(b) and are the system equivalent dynamic natural frequencies varying with Ω

已有研究表明较大间隙可以给系统带来复杂的非线性响应行为[28],而轴承游隙δ0是系统的基本参数之一.取δ0=6.0μm,采用嵌入弧长延拓的HB-AFT方法结合Floquet理论分析系统x方向主共振区间的周期运动及其分岔行为.如图4所示,随着控制参数Ω的变化,稳定的VC周期1解分枝的Floquet乘子在A1(见表2)、A2点通过-1离开单位圆,由亚临界倍周期分岔失稳产生的VC周期2解分枝依然包含多个失稳区间,这与图5(a)的数值分岔图结果是吻合的,其中不稳定周期2解A1-A2段是在A1、A2点由二次Hopf分岔失稳产生的.

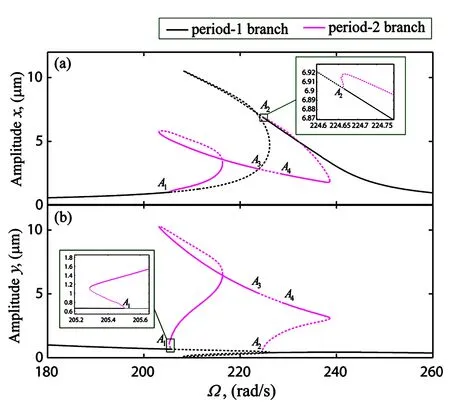
图4 当δ0=6.0μm时,(a) x方向、(b) y方向稳定(实线)和不稳定(虚线)的周期解频响峰峰值曲线Fig.4 For δ0=6.0 μm,stable (solid) and unstable (dashed) periodic frequency-response peak to peak curves in (a) x direction and (b) y direction

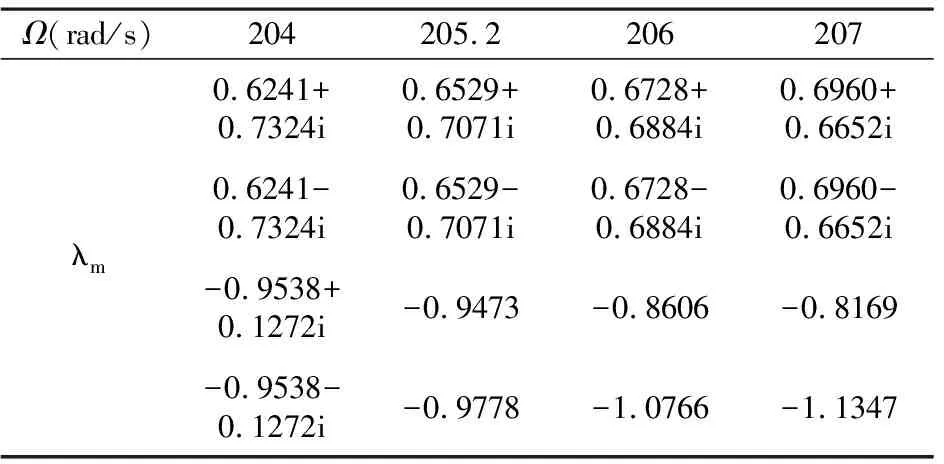
表2 周期1分支在转向点A1附近的 Floquet 乘子λmTable 2 Floquet multipliers λm of period-1 branch around the turning point A1

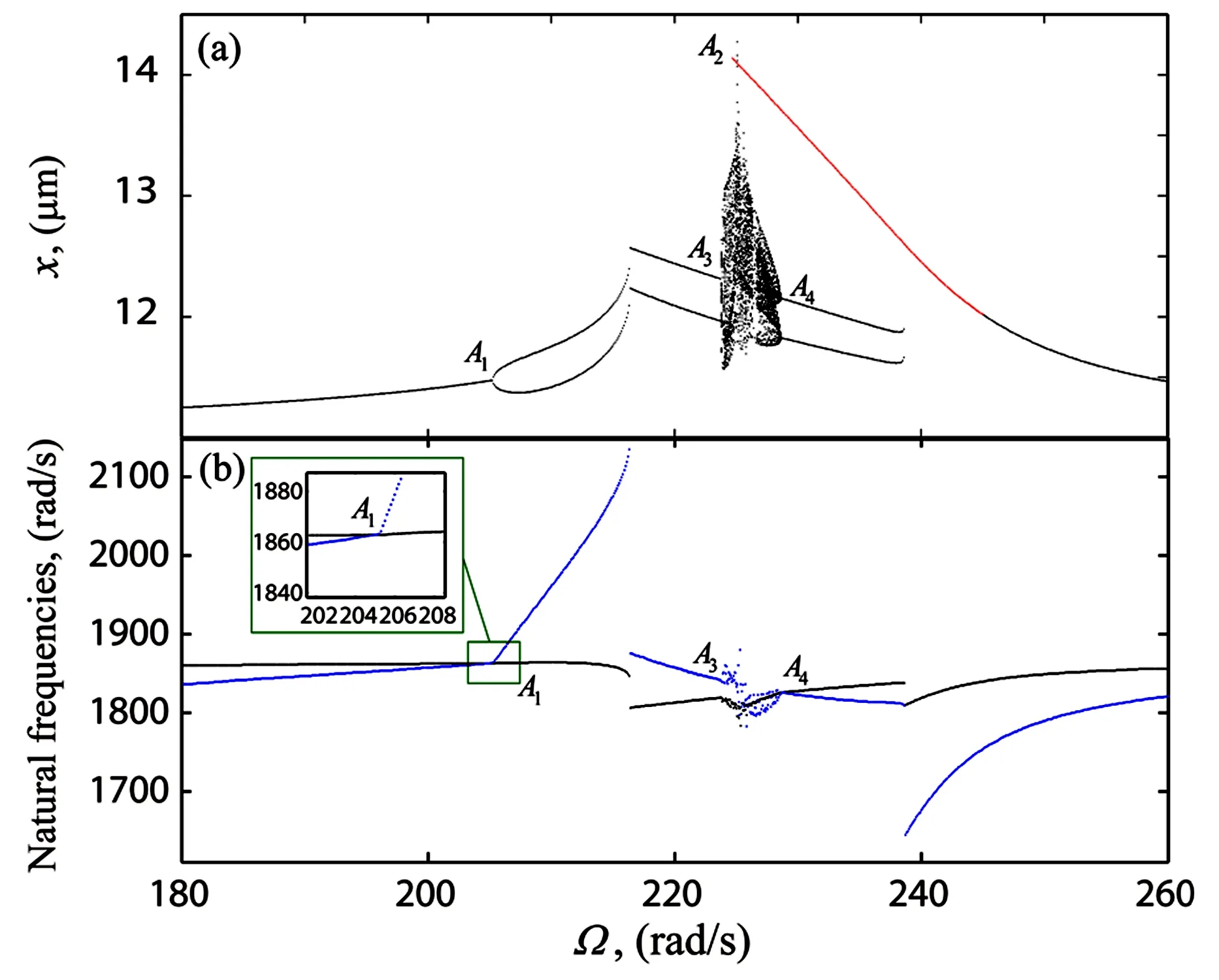
图5 当δ0=6.0μm时,(a) x(t)的数值分岔图,其中黑点、红点分别为向上、向下扫频的数值积分结果,(b)系统动态等效固有频率随Ω的变化值Fig.5 For δ0=6.0 μm,(a) bifurcation diagram of x(t) calculated by numerical integrations when Ω sweeping up (black dots) and down (red dots),and (b) the system equivalent dynamic natural frequencies and varying with Ω

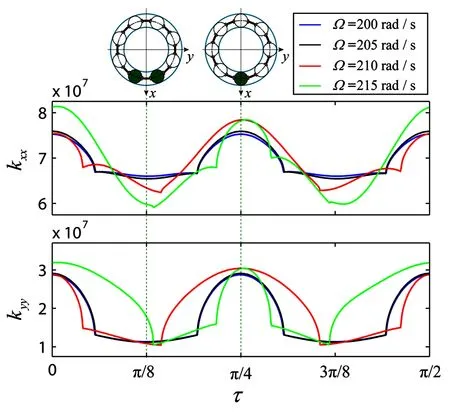
图6 当δ0 = 6.0 μm时,系统在Ω 取180 rad/s、200 rad/s和220 rad/s时的动态刚度,其中τ = Ω tFig.6 For δ0 = 6.0 μm,the system dynamic stiffness when Ω takes 180 rad/s,200 rad/s and 220 rad/s,here τ = Ω t

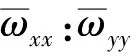
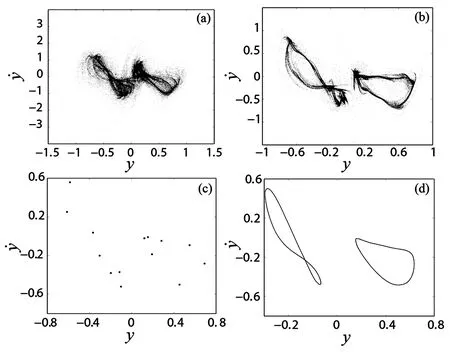
图7 当δ0 = 6.0 μm时,系统在Ω取(a)225 rad/s、(b)226 rad/s、(c)226.5 rad/s和(d)227 rad/s时响应的Poincare映射Fig.7 For δ0 = 6.0 μm,Poincare maps of the response for Ω at (a)225 rad/s,(b)226 rad/s,(c)226.5 rad/s and (d)227 rad/s

4 结论

球轴承非线性因素带来的滞后共振行为会给轴承-转子系统带来突跳、冲击作用,进而可对转子的运行稳定性和安全性带来影响.因此,分析此非线性系统的动态刚度特性,对于预测乃至避开系统的VC接触共振区间具有重要意义.在本文中,针对轴承非线性时变刚度特性对系统VC共振及其分岔行为影响的专门研究尚少的情况,采用理论和数值方法相结合,深入探讨了系统动态刚度特性与主共振区间复杂运动分岔行为的内在关联.研究指出非共振区间的动态等效固有频率对于预测系统VC接触共振位置具有一定的参考价值.另外,发现当系统不同自由度方向上的固有频率值接近1∶2比例关系时,系统可能产生强烈的内共振,进而诱发响应的周期倍化分岔甚至准周期、混沌振动.该研究对球轴承复杂共振响应的控制具有潜在的理论意义和工程价值.