弹支-刚性转子系统过共振瞬态响应特性研究*

王美令 温保岗 韩清凯

(1.大连交通大学 机车车辆工程学院, 大连 116028) (2.大连工业大学 机械工程与自动化学院, 大连 116034)(3.大连理工大学 机械工程学院, 大连 116024)

引言

随着高速旋转机械效率的提高,对于转速的要求也越来越高,其转子系统往往超临界转速运行,在启停过程不得不要多次通过临界转速,然而亚共振向超共振过渡的共振区瞬态振动响应特性比稳态响应复杂得多,在高速旋转机械的设计、研制、运行过程中引起了广泛关注[1,2].

方之楚[3]研究了单盘转子系统过临界的非定常运动,并讨论了陀螺效应和内阻尼对系统瞬态响应的影响.Genta[4]基于有限元法建立了转子系统瞬态响应模型,并考虑了转子非线性影响.Zhou[5]建立了Jeffcott转子系统的瞬态响应解析模型,将瞬态振动响应分解为自由振动和同频振动和伴随振动三部分.郑龙席[6]运用传递矩阵法建立了双盘转子系统的运动微分方程,分析了不平衡量、加速度、支承刚度、阻尼、支承位置等参数对转子瞬态响应的影响.岳聪[7]从越过临界转速时的瞬态动挠度以及进动角随阻尼系数角度分析转子系统的瞬态响应特征.然而目前针对瞬态响应特性的分析主要集中在振动幅值的特性分析,没有进一步研究瞬态过程的相位规律性.

对于支承刚度远低于转子刚度的转子系统,如航空发动机转子系统,通过低阶临界转速时,变形大部分集中于弹性支承上,从而保证系统的高可靠稳定运行,这类转子系统可视为弹支-刚性转子系统[8],其动力学特性有其独特性.蒋书运等[9]采用整体传递矩阵-动态子结构法分析航空发动机整机瞬态响应特性,导出支承子结构运动方程,考虑挤压油膜力,并分析了不同转速、油膜间隙等参数条件下轴心轨迹特点.张华彪[10]针对航空发动机转子叶片掉块故障,进行突加不平衡引发碰摩的瞬态响应分析,并考虑了支承刚度非线性影响.刘政等[11]针对航空发动机特殊的径向转动惯量大于轴向转动惯量的厚盘转子系统,计算了单-厚盘转子分别以定角加速度和定功率过两阶临界转速时对不平衡激振力的瞬态响应,主要讨论了瞬态轴心轨迹变化规律,而忽略了其中的相位特征变化.

本文以结合弹支-刚性转子系统的动力学特点,利用Lagrange能量法建立了考虑变速特性的转子系统瞬态响应动力学方程,区别考虑了非旋转阻尼和旋转阻尼的影响.通过精细积分算法计算获得了加速过临界区的转子瞬态响应幅值、相位随角加速度和非旋转阻尼比、旋转阻尼比的变化曲线,得出角加速度和阻尼在加速过共振区时系统响应特性的影响规律,为带弹支-刚性转子系统的高速旋转机械在设计、运行、维护以及故障诊断等工程实际提供参考.

1 弹支-刚性转子系统瞬态动力学分析

转子系统模型如图1(a)所示,两支点刚度分别为k1,k2(N/m),两支点间的距离为l(m).轮盘中心点C距左支点B1的距离为a,距右支点B2的距离为b.建模过程中坐标系：OXYZ——固定坐标系；Cξηζ——跟随转子一同旋转的动坐标系.坐标系变换关系如图1(b)所示,其中θy、θz、θ分别为转盘绕Cy、CZ、Cx轴的旋转角.

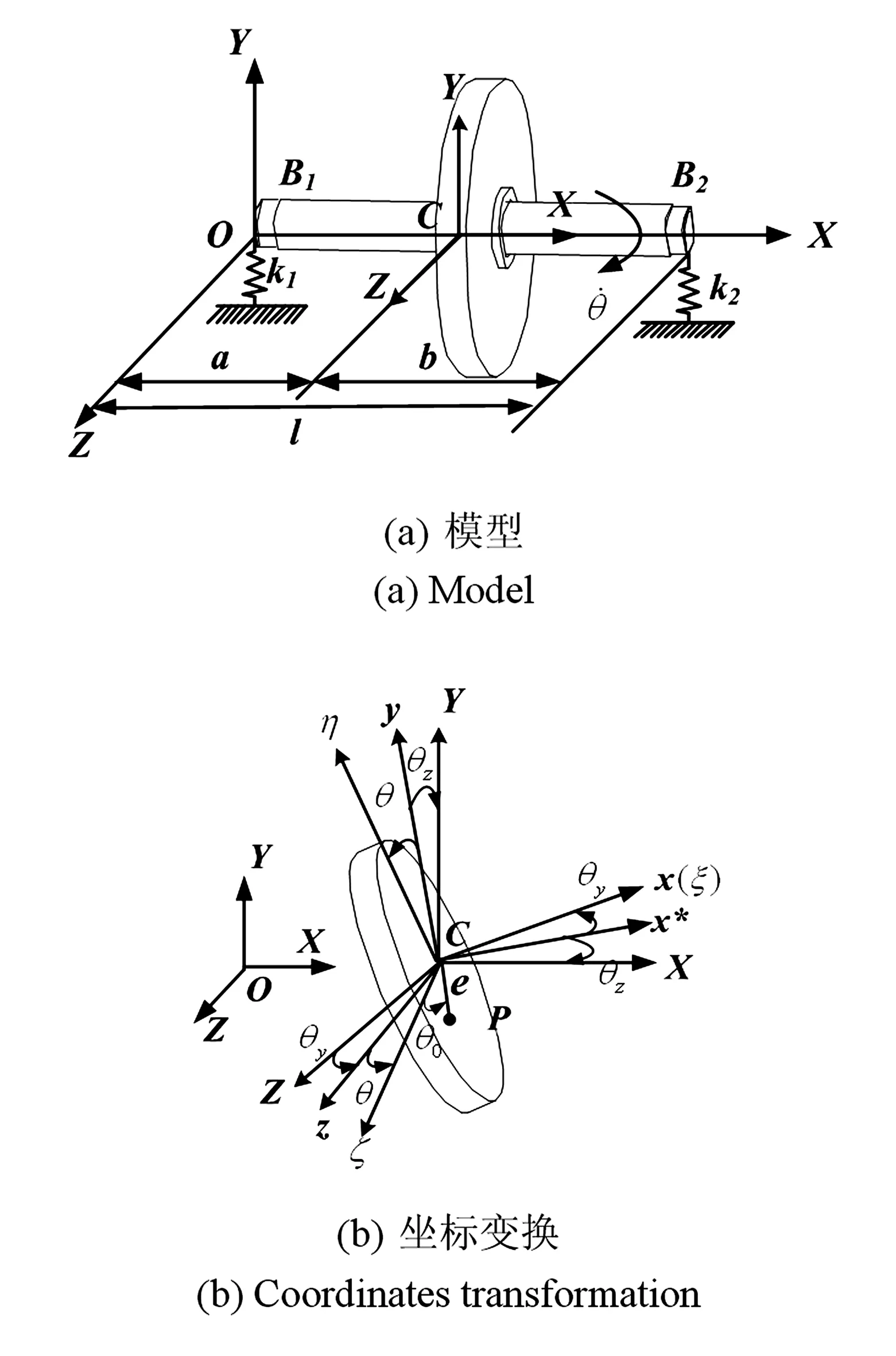
图1 弹支刚性转子系统示意图Fig.1 The rigid rotor system with flexible supports

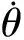
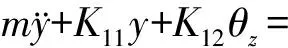
(1)

式中,m(kg)转盘的质量,Jp、Jd(kg·m)分别为转盘的极转动惯量和直径转动惯量,e为转盘的质量偏心量,θ0为其初始相位角.刚度系数可通过对柔度系数矩阵求逆获得,当两支点相同、且转盘位于转轴中央时,即k1=k2=k,a=b=l/2,可得K11=12EIk/(6EI+2a2k),K12=K21=0,K22=12EIka2/(6EI+2a2k).

式(1)的矩阵形式可记为,

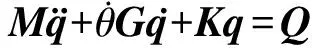
(2)

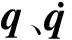
(3)

当考虑与转子相关的旋转阻尼以及与静子相关的非旋转阻尼[4]时,可通过在系统方程(3)的右侧加上广义的阻尼力,假设为粘弹性阻尼,则系统的非旋转阻尼力Fn和旋转阻尼力Frηζ分别可表示为:

(4)

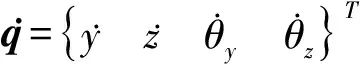
(5)

式中,

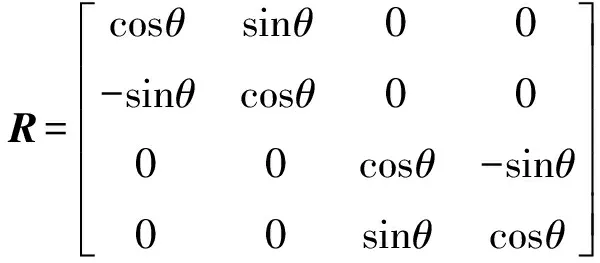
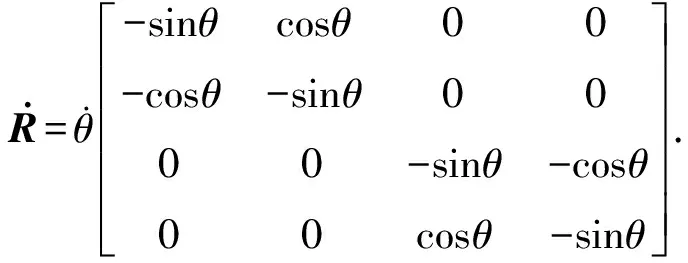
将旋转阻尼力和非旋转阻尼力引入到系统中,系统动力方程式(3)变化为

(6)

式中,阻尼矩阵C、Cr分别为:

(7)

式中,ζn、ζr分别为非旋转阻尼比和旋转阻尼比.

2 弹支-刚性转子系统过共振瞬态响应特性

本节针对弹支-刚性转子系统起停过程中通过刚体模态临界转速的特点,基于建立的系统瞬态动态力学方程,采用增维精细积分方法[12,13],分析从某一转速状态线性加速过临界时,转子系统的瞬态响应幅值及其相位变化特点.

2.1 算例

针对图1所示的弹支-刚性转子系统,分析其加速过共振瞬态不平衡响应特性,所采用的模型参数如表1所示,计算获得系统的前两阶固有频率分别为34.32Hz、71.17 Hz.

表1 转子系统的模型参数Table 1 Parameters of the rotor system

2.2 系统阻尼的影响特性比较

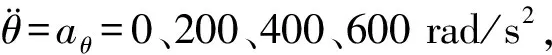
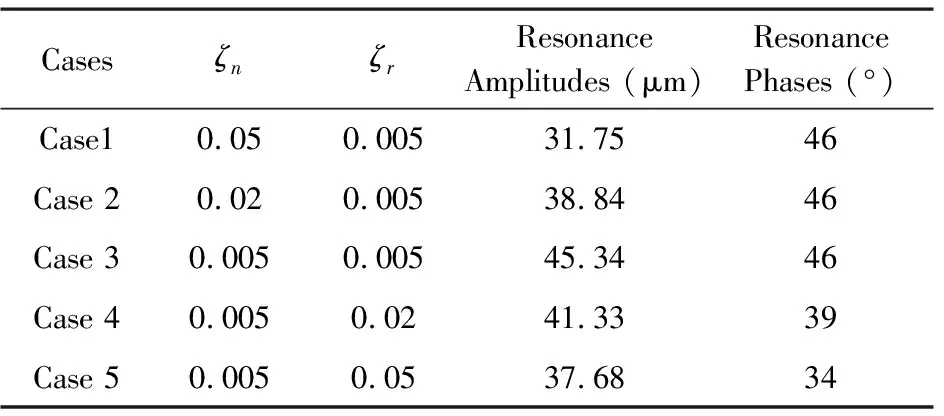
表2 转子系统的阻尼条件及其响应幅值、相位统计结果比较Table 2 Damping conditions and corresponding amplitudes and phases results across resonance

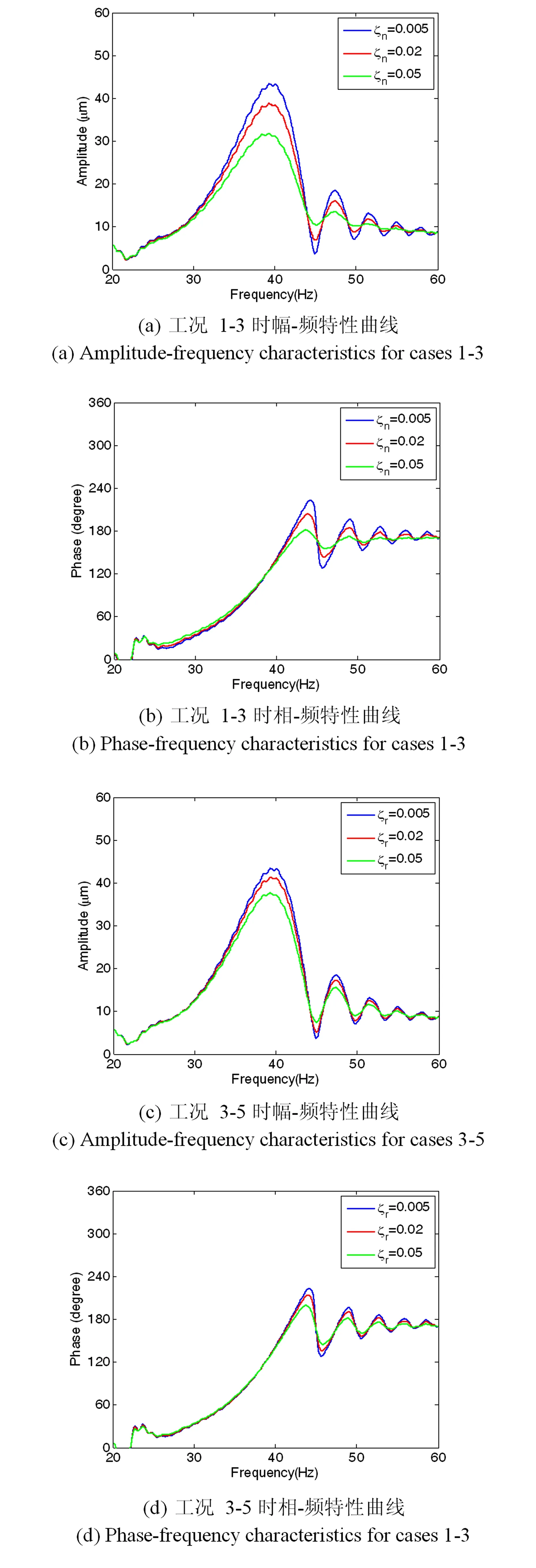
图2 不同阻尼条件下系统过共振响应结果比较Fig.2 Transient responses of rotor systemacross resonance with different damping conditions

通过表2和图2比较结果可以看出：系统加速过临界区时,(1) 瞬态响应最大幅值受非旋转阻尼比ζn和旋转阻尼比ζr影响,且过共振瞬态响应幅值随着阻尼增大明显减小； (2) 在相-频图中稳态响应过临界点有典型的90°相位角,而过共振过程中,过临界点出现新相位角,此相位不受ζr的影响,但随着ζn的增大而增大.

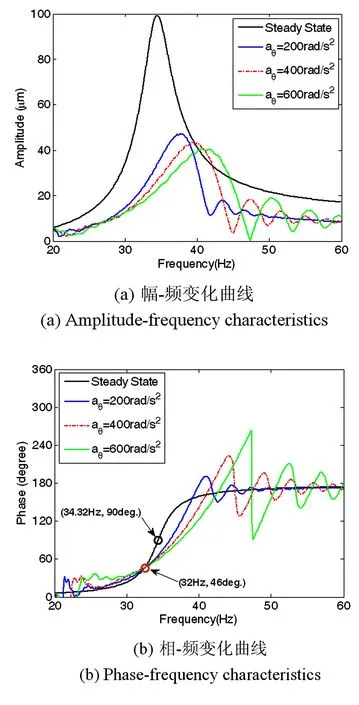
图3 系统在不同加速工况过共振瞬态响应曲线(工况3：ζn= 0.005,ζr=0.005)Fig.3 Transient responses of rotor systemacross resonance with acceleration rates(Case 3：ζn= 0.005 and ζr=0.005)

通过上述分析进一步得出：弹性-刚性转子系统过共振瞬态响应的最大振幅随着加速度值的增大而减小,表明越快速过共振瞬态响应幅值反而小；(2)加速过共振不再呈现典型的90°相位角,而是在临界转速附近出现一个新的相位角,此相位不受加速度值和旋转阻尼比ζr的影响,但随着非旋转阻尼比ζn的增大而增大.

3 结论

(2)瞬态过共振响应幅值明显小于稳态响应幅值,受过共振加速度、非旋转阻尼比ζn和旋转阻尼比ζr的影响明显,且越快速过共振瞬态响应幅值越小.

(3)瞬态过共振区时,在相-频图中临界转速时也没有典型的90°相位角,而是在临界转速附近出现一个新的相位(加速过共振小于90°),此相位不受角加速度值和旋转阻尼比ζr的影响,但随着非旋转阻尼比ζn的增大呈增大趋势.