带有星型齿轮传动结构的转子系统不平衡耦合振动分析*

王梓卉敏 张昊 马平平 陈东洁 翟敬宇 韩清凯†

(1.大连理工大学 机械工程学院, 大连 116024) (2.辽宁工业大学 机械工程学院, 锦州 121001)

引言

齿轮传动风扇发动机(Geared Turbofan, GTF)[1-4]是商用航空发动机的重要发展方向,其中低压转子系统是该发动机的核心部件,为具有星型齿轮传动结构的三支点转子系统.该系统与传统航空发动机的低压转子系统相比,由于星型齿轮减速箱中齿轮啮合作用具有一定影响,使得其动力学特性更加复杂.星型齿轮传动系统中作为输入端的中心齿轮以及作为输出端的环形齿圈同时与多个游星齿轮相啮合,齿轮转子在不同的相位角下相互耦合,齿轮的啮合特性将影响整个转子系统的振动.同时,在发动机实际加工、装配和使用过程中,转子不平衡难以避免,且转子系统往往运转在多个不平衡激励力同时作用的情况.作为转子系统重要的传动部件,不可避免的不平衡外部激励将影响齿轮副之间的啮合力,同时不平衡也会加强齿轮啮合作用对转子系统影响.

近年来,国内学者对星型齿轮传动系统的动态特性进行了研究[5-7],对这类齿轮传动风扇发动机转子系统动力学特性的研究较少.在以GTF发动机转子系统为对象的相关研究中,除了结构与技术特点的概括分析,一些学者基于仿真模型分析了该低压转子系统的动力学特性,但多为提取单转子[8,9]进行研究,或者采用的低压转子模型对齿轮传动系统进行了大量简化.对于此类系统的振动问题,如果不综合考虑齿轮结构耦合振动的影响,会忽略一些重要的动力学特性[10].

本文基于某齿轮传动风扇发动机低压转子模型试验器,考虑齿轮副的动态啮合激励,建立具有星型齿轮传动结构的三支点转子系统有限元动力学模型；进行动力学分析求解并结合试验,研究低压转子系统不平衡耦合振动特性,对多相位不平衡矢量激励下齿轮啮合力的变化进行了分析.本文可为GTF发动机低压转子系统耦合振动分析、动平衡与动态设计优化提供理论支持.

1 转子系统动力学模型的建立

如图1所示,该转子系统由风扇转子、低压压气机-涡轮转子及齿轮转子三部分构成,分别支承.

其中,环形齿圈作为输出端与风扇转子相连,风扇转子采用1支点悬臂支承；低压压气机-涡轮转子采用0-1-1支承方式,与输入端中心齿轮相连[4].基于传统的数值仿真建模方法,对转子系统的轴段采用梁单元模型；盘以及齿轮采用集中质量模型；根据轴瓦油膜力的动力学作用原理,当忽略轴承质量时,在转子系统有限元模型中,通常情况下可将轴承简化为作用在转子支承处的弹簧-阻尼系统.通过刚度组集可得到整体模型[11,12].

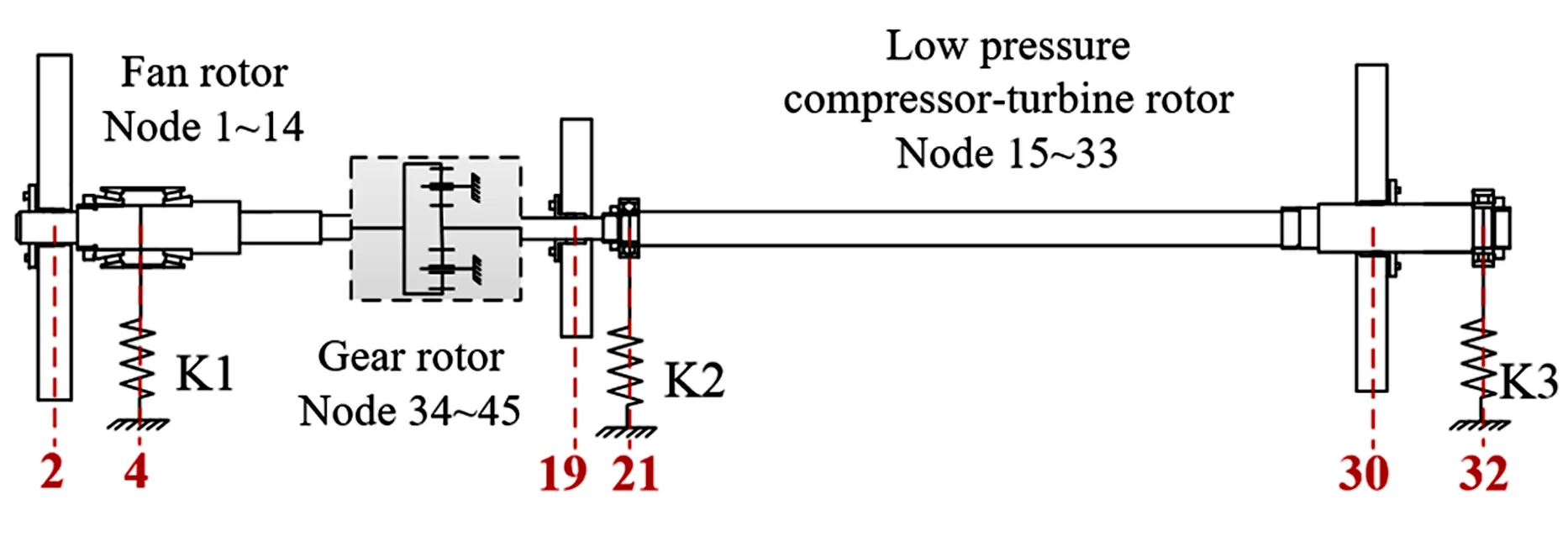
图1 具有星型齿轮传动结构的三支点转子系统模型Fig.1 The model of a three-support rotor with star gear transmission system

其中,齿轮啮合单元为四路分流式星型齿轮传动结构,包括一个中心齿轮,四个游星齿轮和一个环形齿轮,共四对啮合齿轮,每对轮齿啮合部分均存在一个弹簧阻尼系统,其力学模型如图2所示.齿轮传动系统还包括4个游星齿轮,其传动参数如表1所示,传动比为3∶1[2,3].

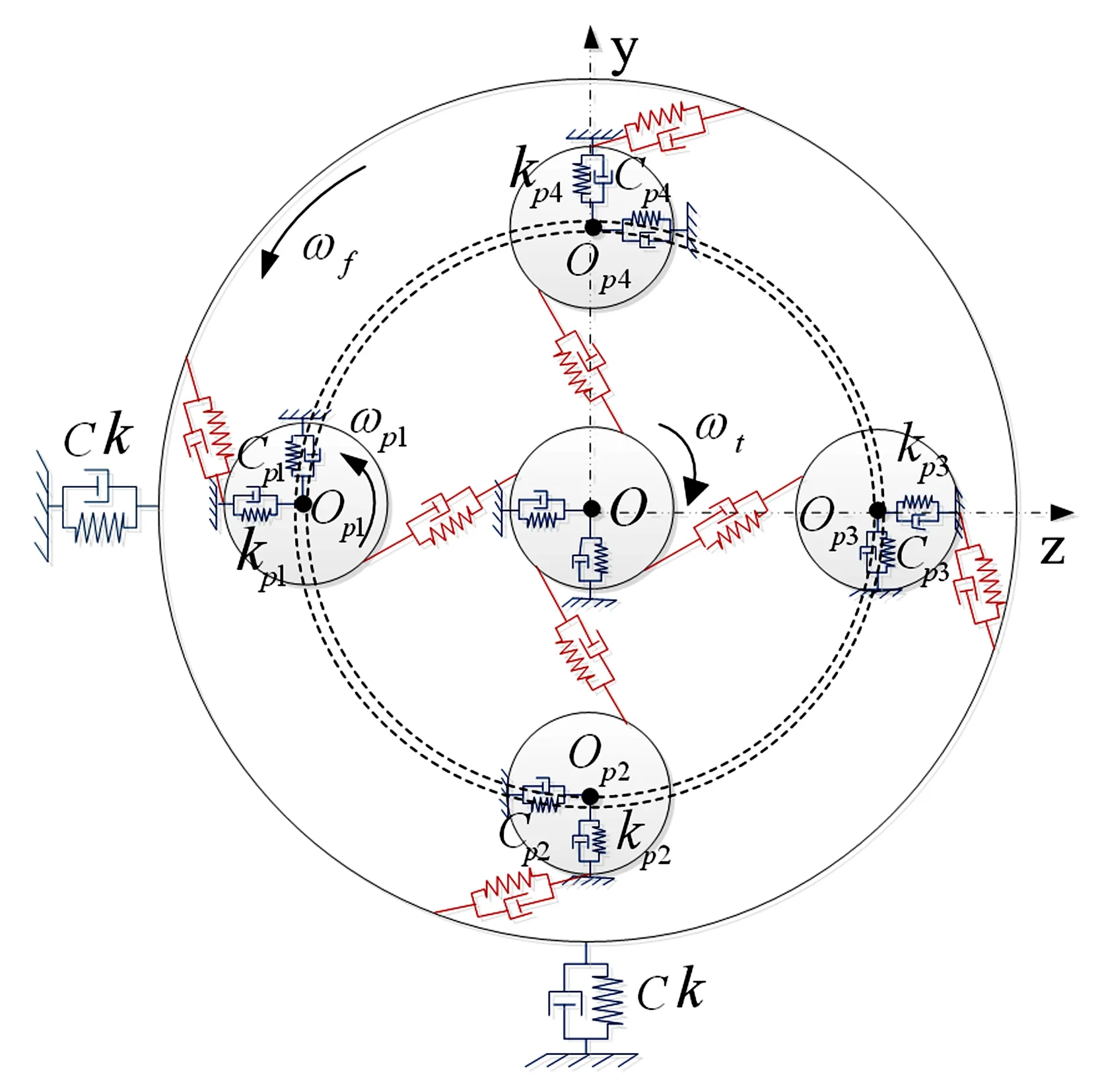
图2 星型齿轮传动力学模型Fig.2 The mechanical model of the star gear transmission system

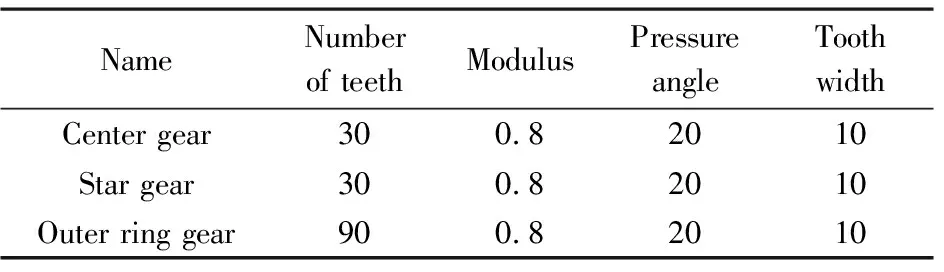
表1 齿轮传动参数Table 1 Gear parameter

以一对啮合轮齿为例,图3为啮合齿轮对动力学模型,具体建模过程如下.

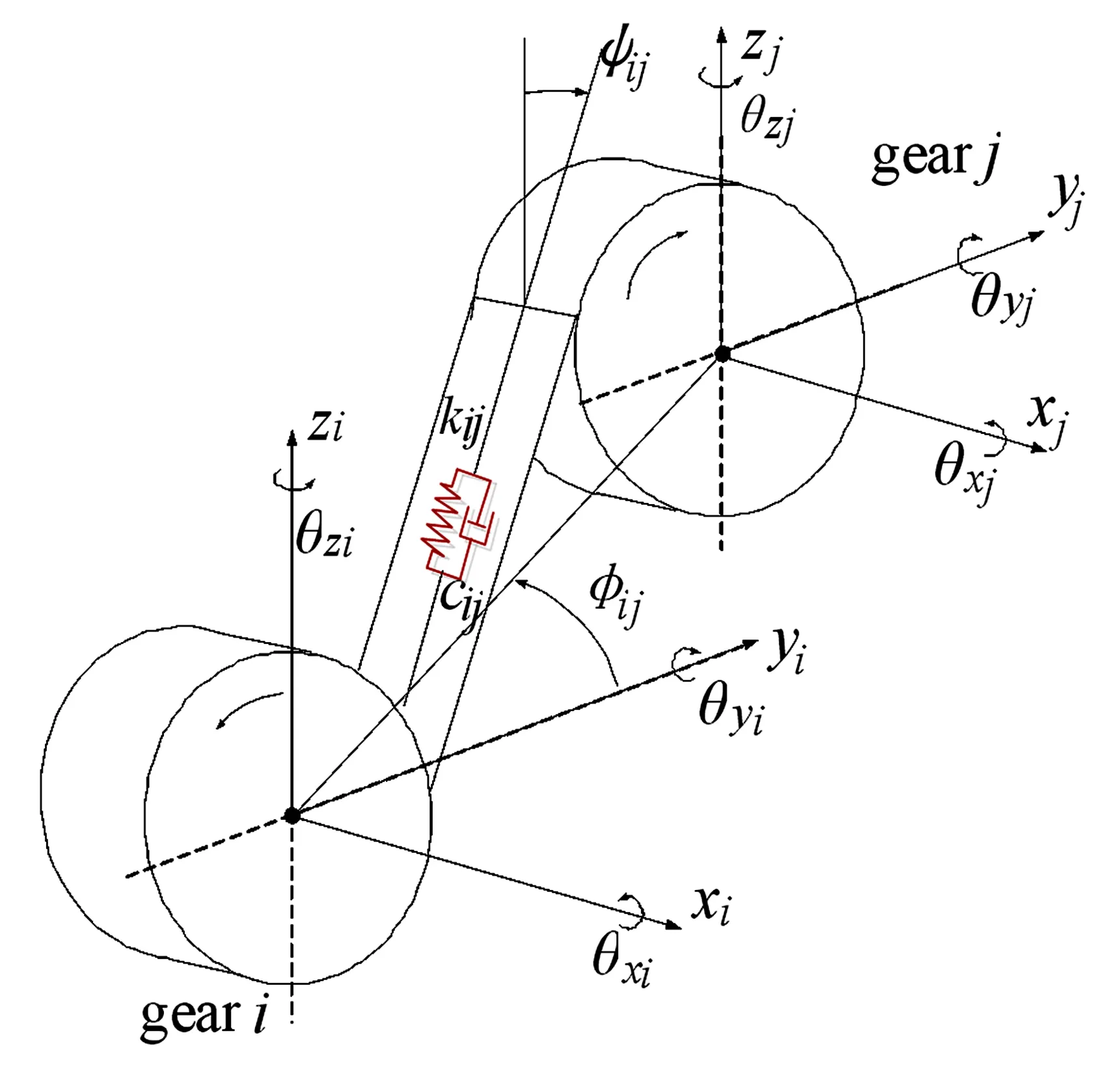
图3 啮合齿轮对动力学模型图Fig.3 The dynamic model of a helical gear pair

如图4所示,i和j为相互啮合的一对直齿轮,其中i为驱动轮,j为从动轮.每个齿轮都具有三个平动自由度和三个旋转自由度,该单元共有12个自由度,u为这对齿轮副单元的位移矢量,表示为式(1)：

u=[xi,yi,zi,θxi,θyi,θzi,xj,yj,zj,θxj,θyj,θzj]T

(1)

上述星型齿轮单齿啮合的动力学模型图中,ψij是z轴正方向到啮合面的方向角,它与驱动轮的转动方向有关,表示为式(2)：

(2)

其中,αij为齿轮压力角,φij是齿轮中心线与y轴正向的夹角,则齿轮副的运动方程为：

(3)

式(3)中,Ti为驱动力矩,kij为齿轮的啮合刚度,即引起单位位移所需的力,cij为啮合阻尼,pij(t)为轮齿沿啮合线上的相对位移,主要由齿轮对扭转引起的变形pijr和横向振动引起的变形pijl组成,表示为式(4)：

pij(t) =pijr+pijl

=sgnriθxi+sgnrjθxj+(yi-yj)sinΨij+

(zi-zj)cosΨij

(4)

其中,ri与rj分别为齿轮i和j的基圆半径,sgn为符号函数,具体表示为式(5)：

(5)

对于齿轮啮合单元,将上述运动方程整理成矩阵形式有式(6)：

(6)

其中,F为齿轮单元广义力向量,Mij和Kij分别为齿轮单元的质量矩阵,阻尼矩阵和啮合刚度矩阵.

由于在实际啮合中,齿轮啮合刚度会随齿轮转动而产生变化,它与齿轮重合度以及单对齿刚度均有关.以本文研究对象中一对相啮合的太阳轮和行星轮为例,取驱动轮转速为6000r/min,根据石川公式[13]计算方法,可得该对齿轮的啮合刚度曲线,如图4所示.

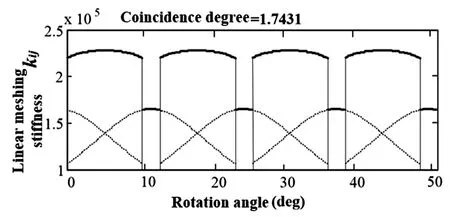
图4 齿轮啮合刚度曲线Fig.4 The curve of the meshing stiffness of gears

该对齿轮的重合度大于1,从上图可以看出,刚度曲线具有明显的跳跃现象,在双齿啮合区同时有两对轮齿参与啮合,刚度为两对轮齿的刚度叠加,此时啮合区较长,平均刚度较大.

本文考虑齿轮啮合刚度的时变性,取一个周期的刚度变化曲线,采用傅里叶级数对其进行拟合,则时变啮合刚度可表示为式(7)：

(7)

2 不平衡激励对转子系统振动的影响

2.1 低压涡轮盘不平衡激励下转子系统的振动响应

首先分析单盘不平衡激励下低压转子系统的振动情况.设置驱动转速为2400r/min,选择对低压涡轮盘施加不平衡量,并改变其不平衡量的大小,分析低压转子系统的振动响应,得到转轴各测点在不同不平衡量下的振幅,如图5所示.

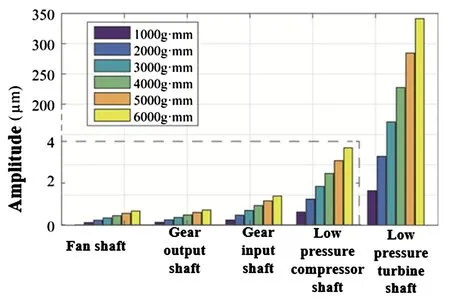
图5 低压涡轮盘不平衡激励下转子系统的振动Fig.5 Rotor vibration information under imbalance of low pressure turbine disk

根据风扇轴、齿轮输出和输入轴、低压压气机轴及低压涡轮轴在各种不平衡加载情况下的振幅变化可明显看出,转子系统在单盘不平衡激励下,振动沿转轴传递并逐渐衰减.此外,由图5知,低压转子系统各测点的振幅均随着低压涡轮盘不平衡量增大呈正比增长,且离振源越近,增长率越大.

2.2 风扇盘-低压涡轮盘不平衡激励对转子系统振动的影响

GTF发动机中,与机匣内部的低压压气机和低压涡轮相比,解决机匣外风扇的不平衡问题更直接,并且若通过风扇配重来解决机匣内转子的振动问题也更容易.由于齿轮减速机输入轴与输出轴的转向相反,即风扇转子和低压压气机-涡轮转子转向相反,针对不平衡相位差的分析无实际意义,故本节仅研究风扇不平衡大小对转子系统振动的影响.

首先,分析低压涡轮盘引起转子不平衡振动的情况,设置低压涡轮盘不平衡量大小为4000g·mm,驱动转速为2400rpm,然后对风扇盘施加不同大小的不平衡激励, 在1000～6000g·mm范围上取值,经仿真计算得到风扇轴、齿轮输出输入轴、压气机轴及低压涡轮轴的振动响应,分析结果如图6所示.

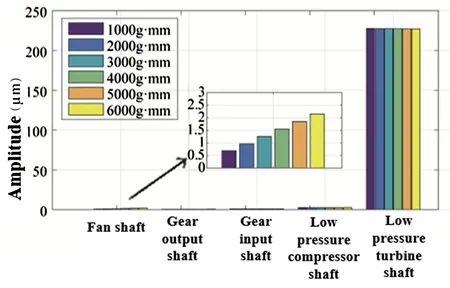
图6 风扇盘与低压涡轮盘不平衡时转子系统的振动Fig.6 Rotor vibration information under imbalance of fan disk and low pressure turbine disk

根据图6可明显看出,除了风扇轴段,其他测点的振动受风扇不平衡量变化的影响很小.结合图5所示,单盘激励分析中低压涡轮盘不平衡量为4000g·mm时各测点的振动情况可知,当风扇盘不平衡量发生改变时,转子系统中除风扇段振动变化较大外,齿轮输出输入轴、压气机轴及低压涡轮轴的振动均保持在低压涡轮单盘不平衡激励时的振幅水平.由此可知,当风扇盘与低压涡轮盘同时存在不平衡量时,低压涡轮盘不平衡对转子系统的振动影响更大.

在同样转速下,分析低压压气机盘与风扇盘同时存在不平衡的情况.选择对低压压气机盘施加6000g·mm大小的不平衡量,研究随着风扇盘不平衡变化,转子系统各测点的振幅,计算结果如图7所示.

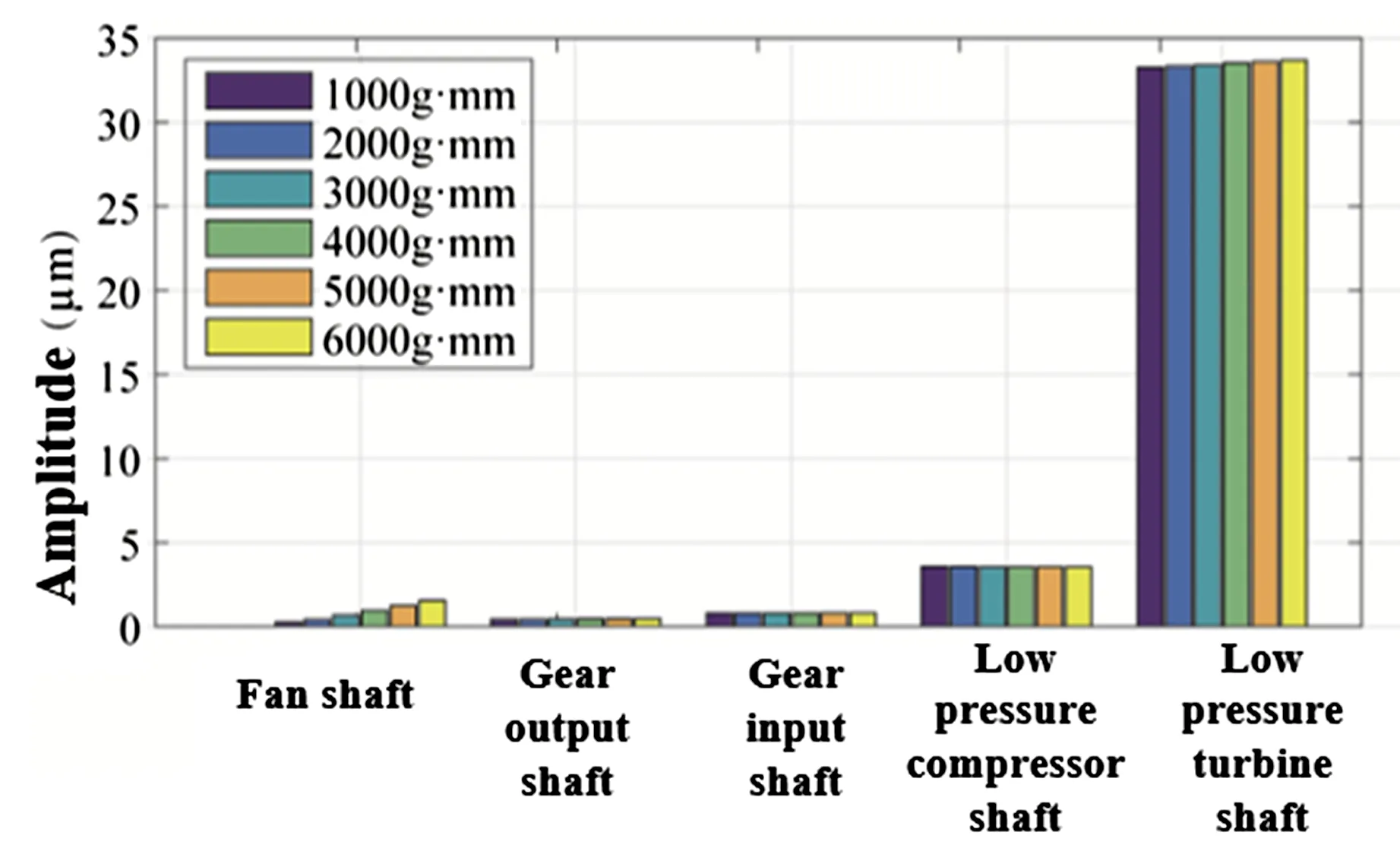
图7 风扇盘与低压压气机盘不平衡时转子系统的振动Fig.7 Rotor vibration information under imbalance of fan disk and low pressure compressor disk

根据图7可知,转子系统各测点的振幅变化和风扇盘与低压涡轮盘同时存在不平衡量的情况具有一致性.风扇不平衡量变化主要对风扇转子的振动产生影响,对低压压气机-涡轮转子的振动影响较小,其实,风扇转子转速仅为低压压气机-涡轮转子转速的三分之一,低压转子系统本身传动特点是造成这种结果的主要因素之一.因此,当GTF发动机低压压气机-涡轮转子存在不平衡量时,通过风扇转子配重难以解决转子系统的振动问题.

2.3 低压压气机-涡轮盘不平衡激励下系统的振动响应

由于低压压气机盘和低压涡轮盘相距较远,若两盘均存在不平衡时情况将复杂化,故针对低压压气机-涡轮转子双盘不平衡的工况,进一步分析低压转子系统的振动响应.对低压压气机施加大小为6000g·mm的不平衡量,通过改变低压涡轮盘的不平衡量,分析其大小和相位变化对风扇轴、齿轮输出输入轴、压气机轴及低压涡轮轴振动响应的影响.设置输入转速为2400r/min,得到各测点的振幅如图8.

由图8可见,转子各测点的振动幅值均在低压压气机不平衡和涡轮不平衡相位差为180°时出现峰值,且在同样的不平衡大小条件下,各测点的振幅随不平衡相位差的变化曲线以x=180°轴对称.其中,风扇转子、齿轮箱输入输出轴以及低压涡轮轴测点在不平衡相位差为180°时振幅最大,低压压气机轴测点的振幅最小.

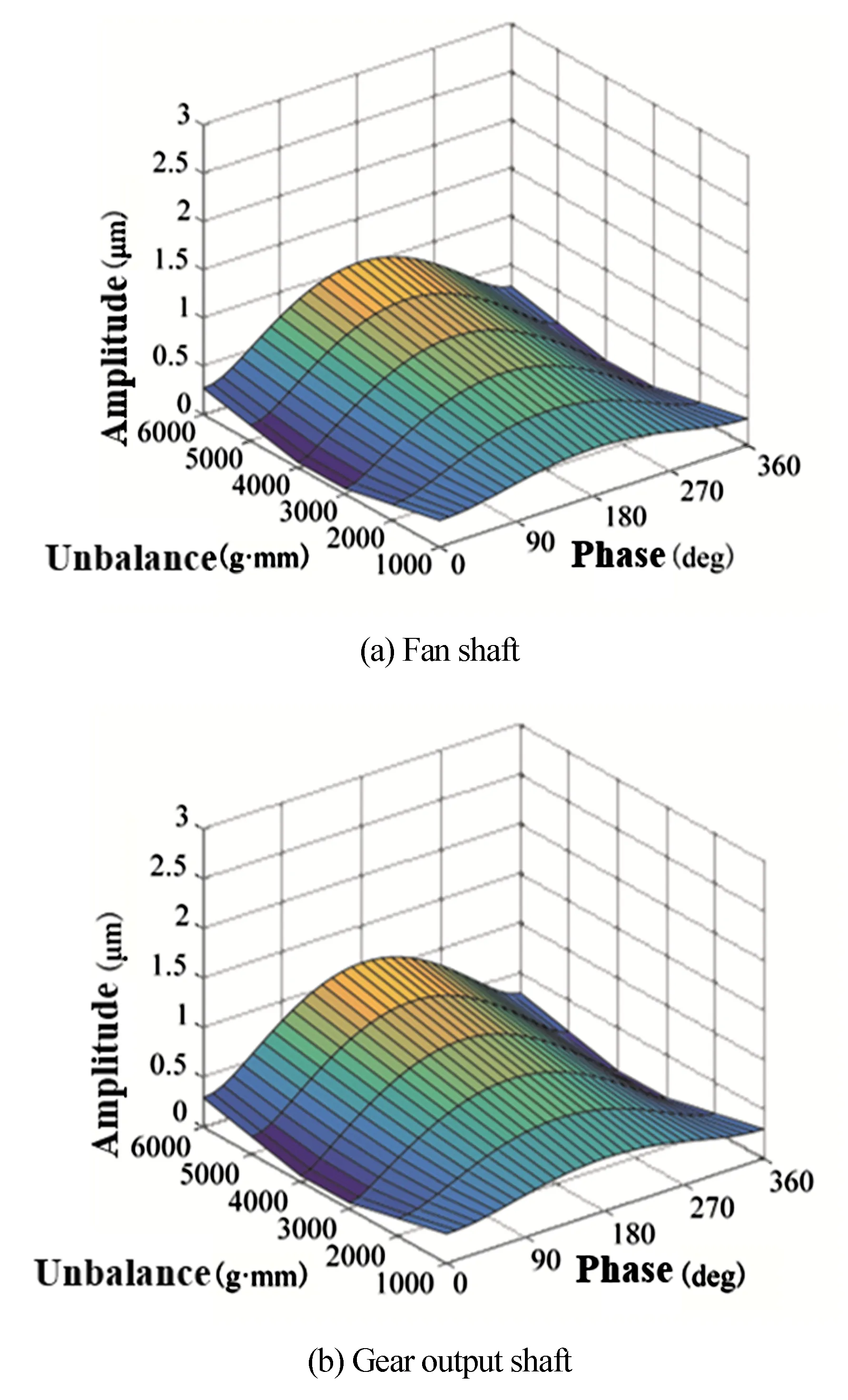
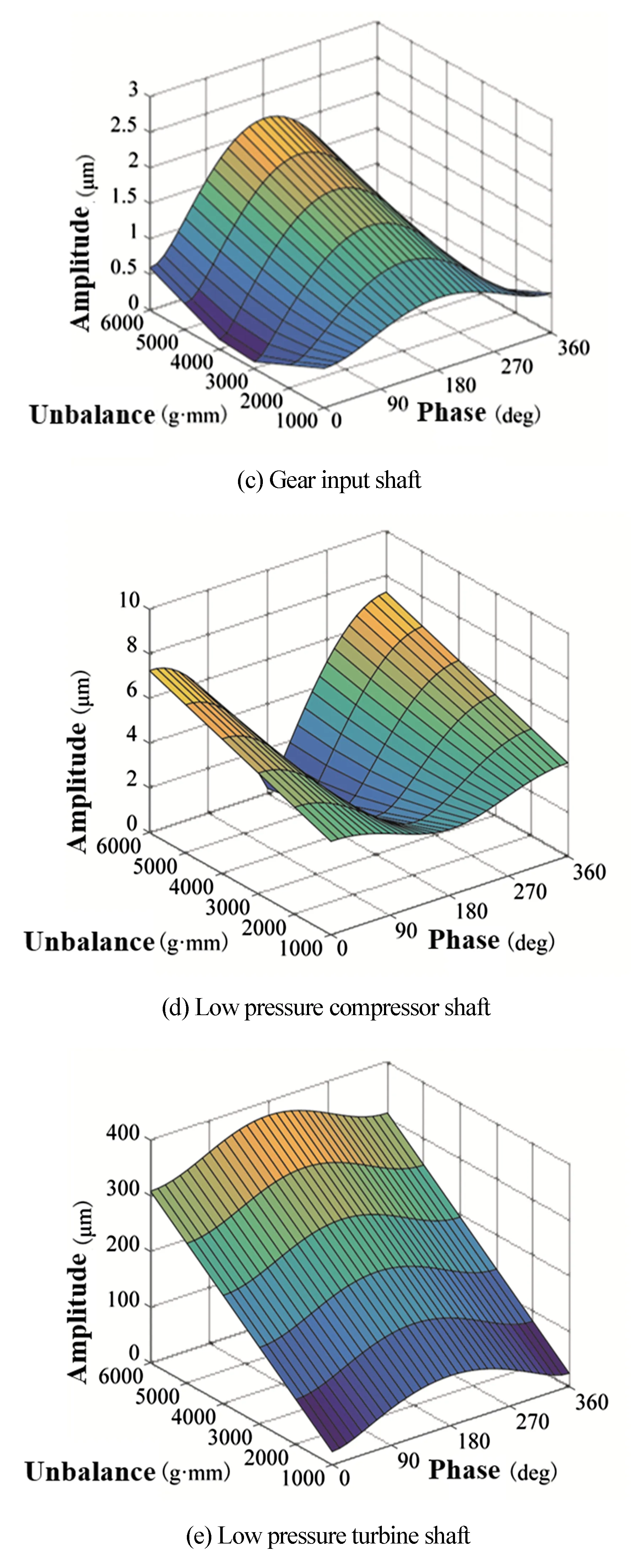
图8 双盘不平衡激励下低压涡轮盘不平衡对转子系统振动的影响Fig.8 Influence of low pressure turbine imbalance on rotor vibration

随着不平衡相位的变化,除了低压涡轮轴处的测点,转子系统其他测点的振动与不平衡大小的关系均在发生改变.其中,当不平衡相位差小于90°、大于270°时,随低压涡轮盘不平衡量的增加,低压压气机轴的振幅增大,风扇转子和齿轮箱输入输出轴的振动先减弱后增强；当不平衡相位差处于90°和270° 之间时,低压压气机轴的振幅随低压涡轮盘不平衡量的增加而减小,而风扇转子和齿轮箱输入输出轴的振动规律变为随之增长.如图8(e)所示,低压涡轮轴随涡轮盘不平衡量的增加成正比增长,不平衡相位差不改变其增长比.

分析上述测点的振动规律与不平衡变量位置的关系,将低压压气机盘不平衡量作为变量,对转子系统中低压涡轮盘施加4000g·mm的不平衡量不变,研究风扇轴、齿轮输出输入轴、压气机轴及低压涡轮轴的振动情况.考虑双盘不平衡激励的相位差对转子系统振动的影响具有对称性,将低压压气机盘和涡轮盘不平衡相位差的变化范围取为0～180°,设置转子转速为2400rpm,计算分布于转子系统各测点的振动幅值,如图9.

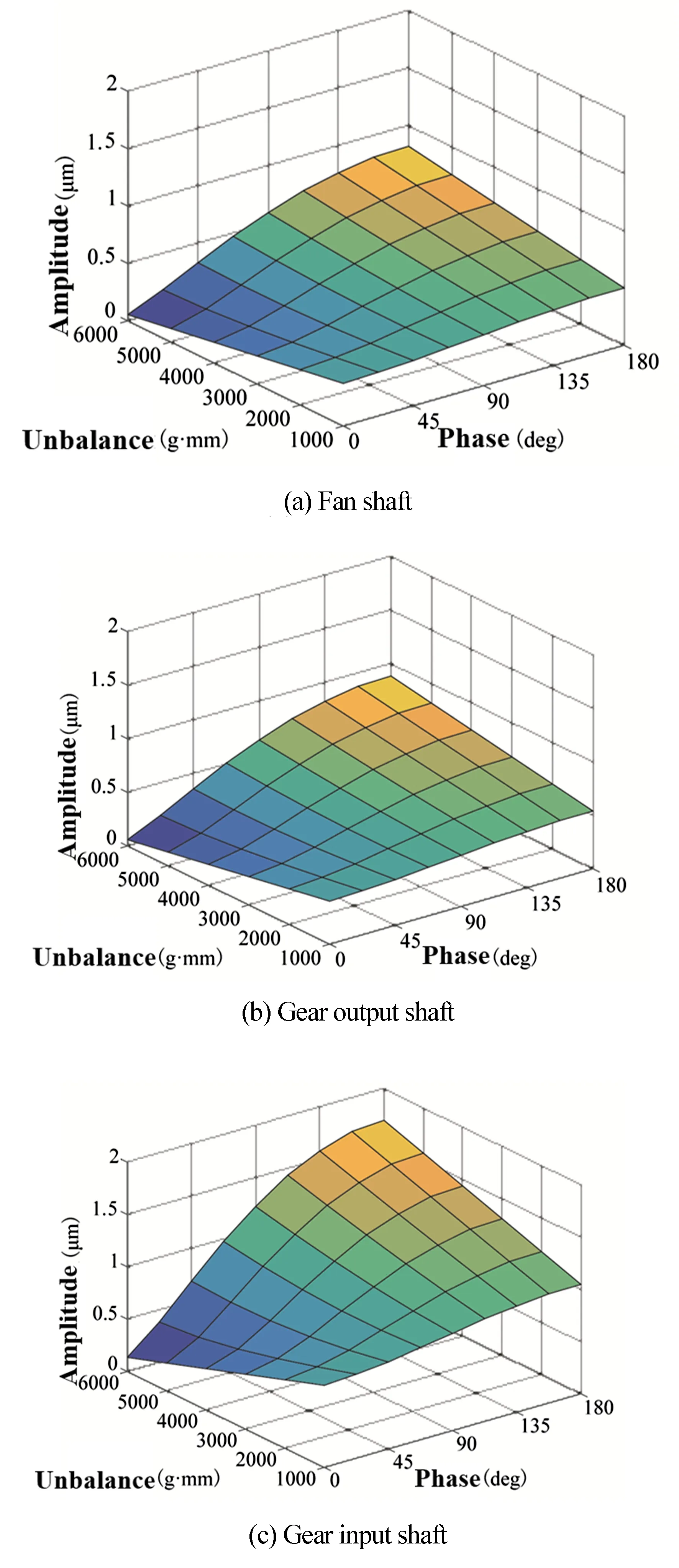
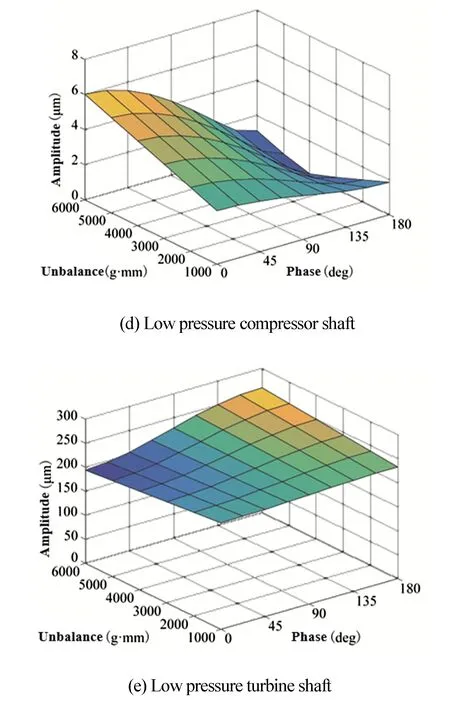
图9 双盘不平衡激励下低压压气机盘不平衡对转子系统振动的影响Fig.9 Influence of low pressure compressor imbalance on rotor vibration

很明显,由于双盘不平衡激励的相位差是互为对照,故图9所示转子系统各测点的振幅随不平衡相位的变化趋势不变.但在不同的不平衡相位差下,风扇轴、齿轮输出输入轴、压气机轴及低压涡轮轴的振动与低压压气机不平衡量大小的关系均发生改变.当不平衡初始相位角小于90°时,随低压压气机盘不平衡量的增加,仅低压压气机轴的振幅增大,风扇转子、齿轮箱输入输出轴以及低压涡轮轴的振幅均减小.其中,结合图5和图9分析低压涡轮轴在各种不平衡状态下的振动情况可知,在一定相位差范围内,低压压气机盘存在不平衡能一定程度的减弱低压涡轮轴段的振动；在低压压气机-涡轮转子双盘不平衡初始相位角大于90°的情况下,风扇转子、齿轮箱输入输出轴以及低压涡轮轴的振幅随低压压气机盘不平衡量的增大而增大,而低压压气机轴的振动先减弱后增强.

综合上述各种不平衡状态下风扇转轴和齿轮输入输出轴的振幅变化图分析,低压压气机-涡轮转子的不平衡对风扇转子和齿轮箱的振动影响规律具有一致性,并且,测点离振源越远,振动越弱.对于处于振源之外的风扇转子,不平衡参数的变化并不改变振动向外传递的递减规律.不平衡量之间的强耦合作用主要发生在低压压气机附近,如图8(d)和图9(d)所示,当低压压气机盘和涡轮盘的不平衡相位差为180°时,存在离振源更近的压气机轴测点比齿轮箱输入轴测点振幅更小的情况.

此外,如图9(e)所示,在同一初始相角下,低压涡轮轴测点的振幅随低压压气机不平衡量的变化较平缓,可知该轴段的振动主要受低压涡轮盘不平衡量的影响.因此,若GTF发动机因低压涡轮盘不平衡造成低压涡轮轴振动乃至整机振动时,通过转子系统的其他部件配重难以解决问题,应当对涡轮盘本体采用主动控制技术.

3 转子不平衡对齿轮啮合力的影响

由于星型齿轮传动系统中四个游星齿轮结构参数均相同,故选取一个游星齿轮研究,其分别与环形齿轮、中心齿轮的啮合效应.为了表达方便,定义环形齿轮和游星齿轮间的啮合力为F14,中心齿轮与游星齿轮间的啮合力为F15.分析如表2所示的三种转子不平衡运行工况下,两组啮合力的时域信号和频域信号.

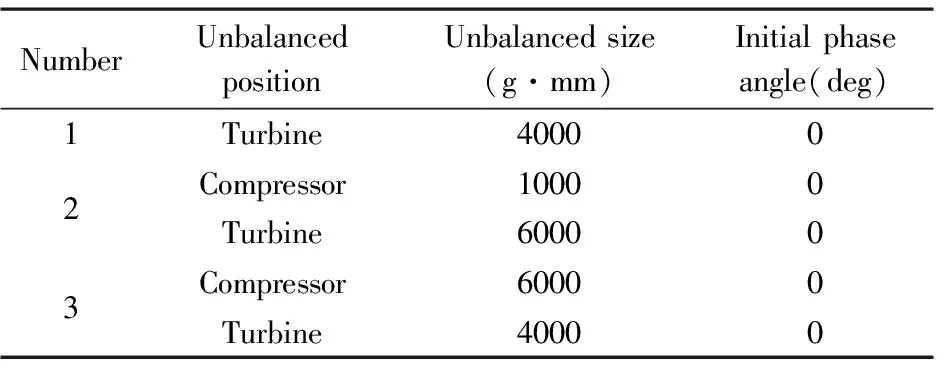
表2 转子系统不平衡工况Table 2 The unbalanced condition of rotor system

由计算结果可知,在转子不平衡的影响下,两组齿轮对之间啮合力存在与不平衡激励有关的周期性,以及与啮合频率相关的小幅波动.由各频域信号可看出,不平衡激励频率占主要成分,说明转子不平衡对齿轮啮合力的影响较大.通过对比不同不平衡加载情况的齿轮啮合力可知,由于受到耦合振动的影响,在图10(c)所示相对较大的不平衡激励下,啮合力峰值反而减小近十倍.并且,对应的具体不平衡工况参数与上一节的转子系统振动分析结果相一致.此外,在上述三种转子不平衡加载形式下,环形齿轮和游星齿轮间的啮合力F14均大于中心齿轮与游星齿轮间的啮合力F15.

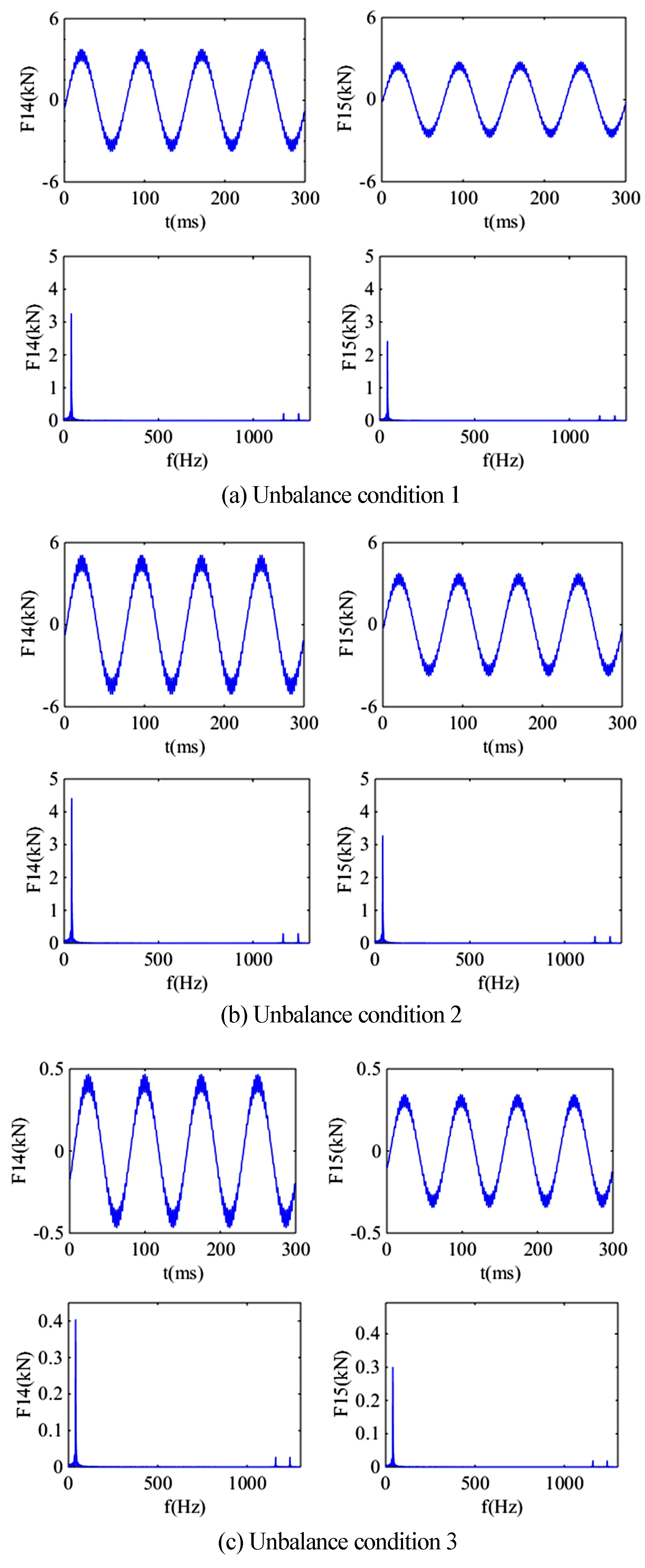
图10 低压压气机-涡轮转子不平衡时齿轮啮合力的时域与频域信号Fig.10 Information of gear mesh force under imbalance of low pressure compressor-turbine rotor

针对表2中低压压气机-涡轮转子双盘不平衡激励的情况,改变其不平衡相位,分析两组齿轮啮合力F15、F14与相位差的关系.

由图11可知,在低压压气机-涡轮转子双盘存在不平衡激励的情况下,齿轮啮合力F15和F14随不平衡相位的变化与转子系统的振幅变化规律一致,均在相位差为180°时达到最大值.图11(a)为低压压气机不平衡较小的情况,此时两组齿轮啮合力随相位差的变化幅度相同,且较平缓.而当低压压气机不平衡增至6000g·mm时,转子不平衡之间产生较强的耦合作用,啮合力受相位差的影响很大,尤其是环形齿圈与游星齿轮之间的啮合力.

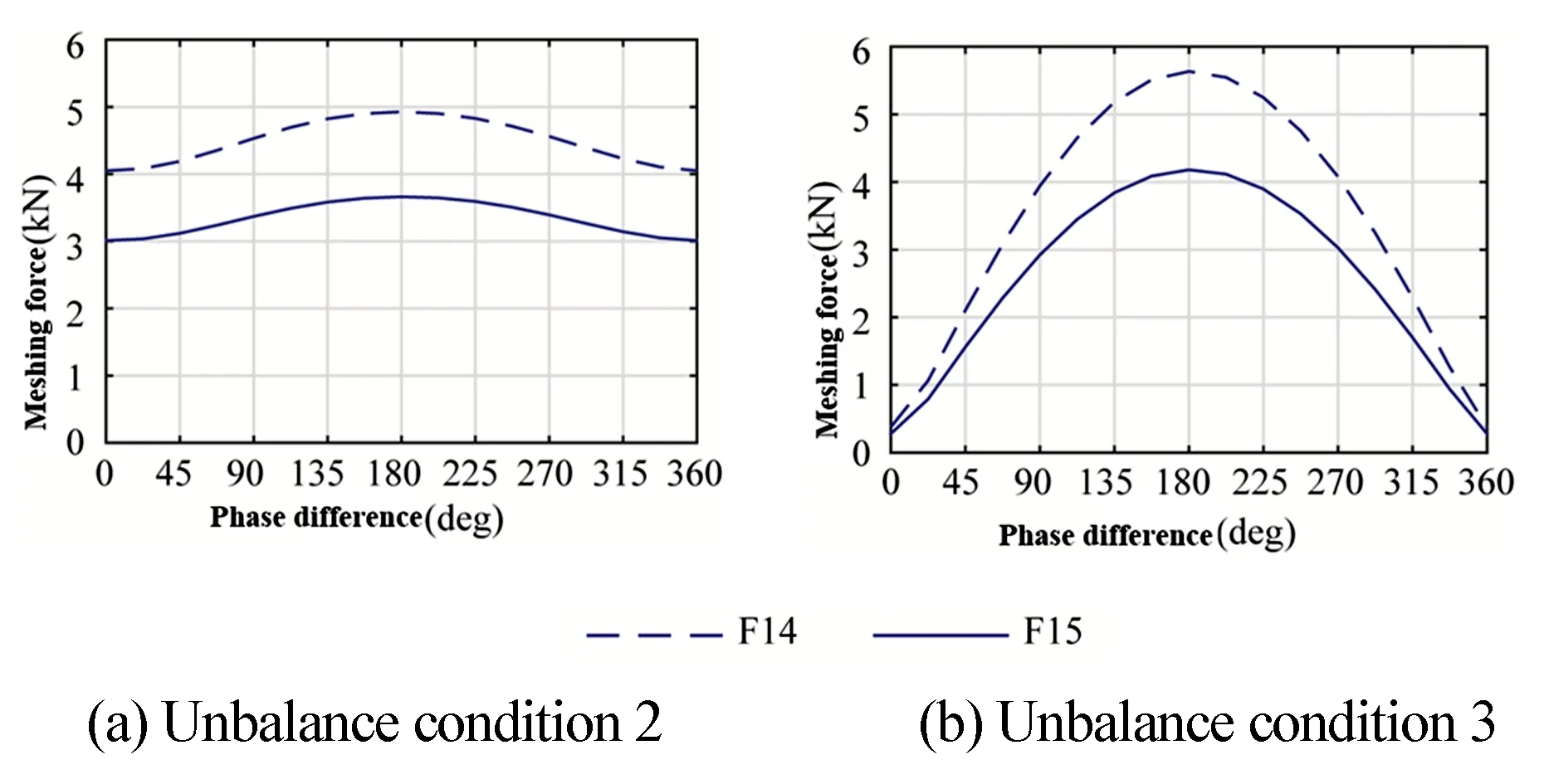
图11 齿轮啮合力与不平衡相位的关系Fig.11 Relationship between gear mesh force and phase angle of imbalance

由于实际发动机转子不平衡不可避免且低压压气机-涡轮转子转速较高,故在齿轮参数化设计中就需要对环形齿圈与游星齿轮的强度要求更严格.

4 不平衡激励下的转子振动试验

低压转子试验器测点布置如图12所示,分别在低压涡轮轴上以及风扇盘附近布置电涡流传感器,获取测点的振动位移信号.

图12 转子不平衡试验测点布置Fig.12 Arrangement of testing points

通过转盘圆周的螺纹孔分别对低压压气机施加和低压涡轮施加不平衡量,其中低压压气机不平衡量大小为6000g·mm,根据仿真分析结果,选择将低压涡轮不平衡量大小取为1900g·mm、3100g·mm、4000g·mm三种情况,且两盘不平衡无初始相位,设置电机转速2400r/min,得到各测点的振动曲线,并对其进行频域分析,结果如图13、14所示.

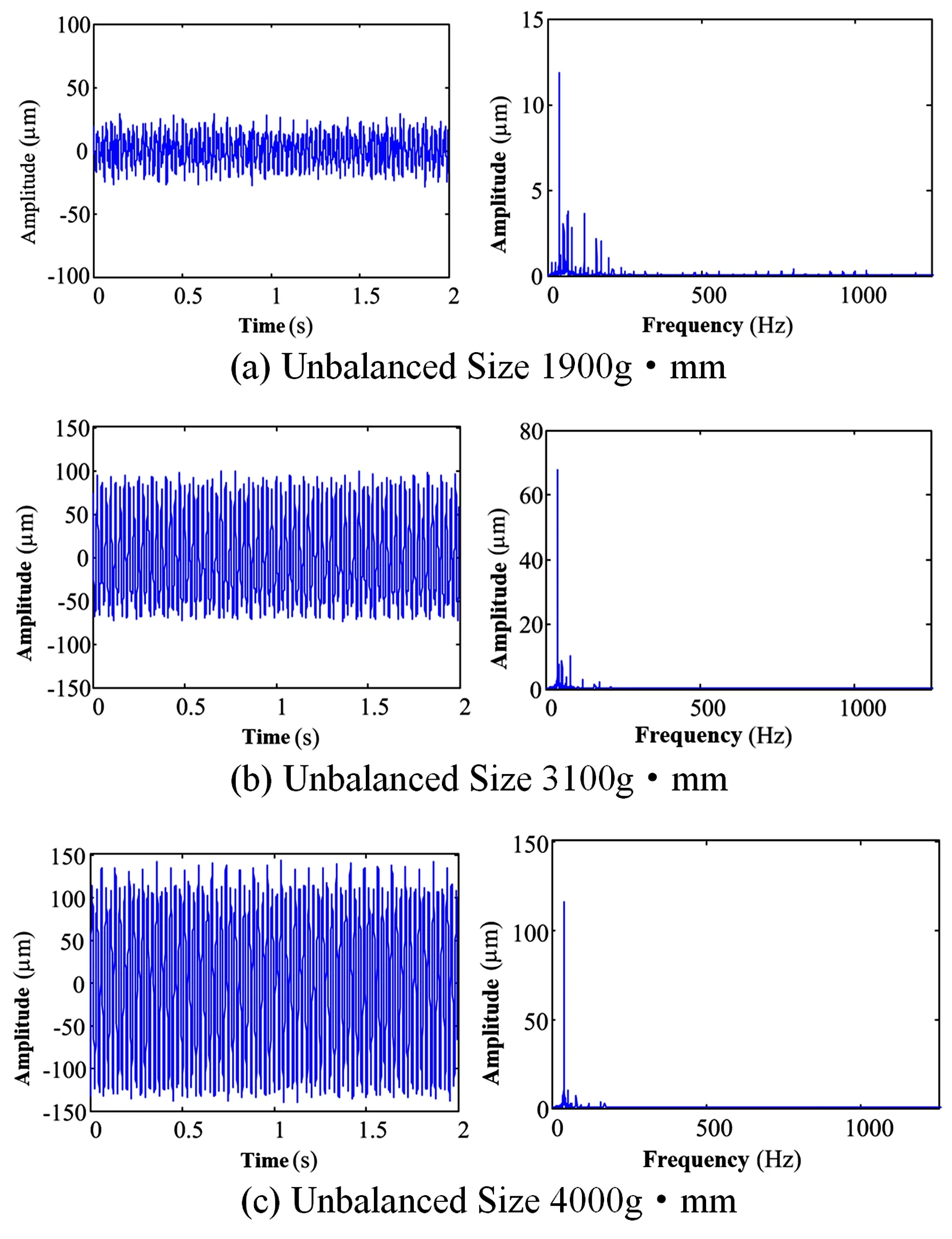
图13 低压涡轮转轴测点的振动响应Fig.13 Vibration response of testing point near low pressure turbine rotor

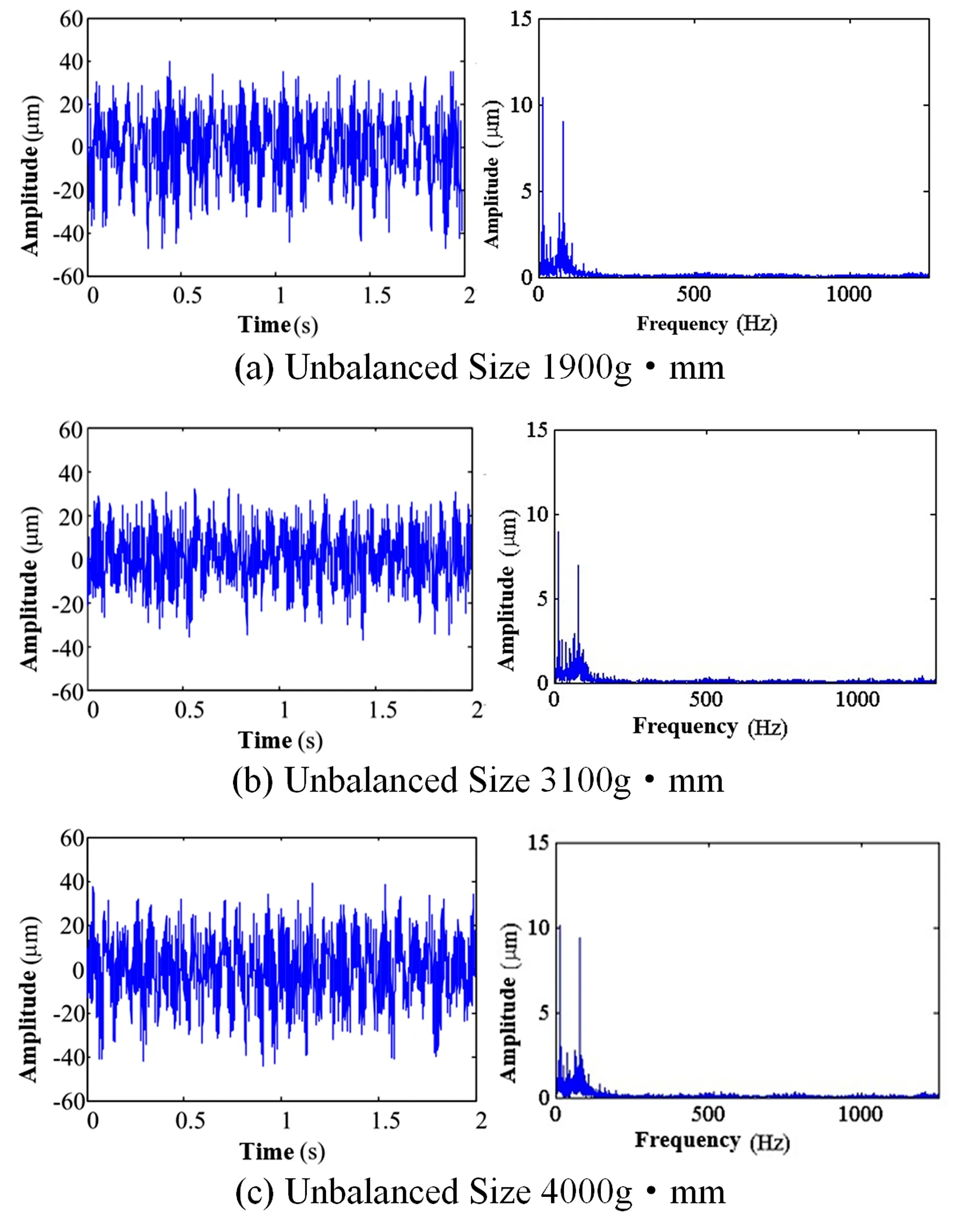
图14 风扇转子测点的振动响应Fig.14 Vibration response of testing point near fan rotor

由图13可知随低压涡轮不平衡量增大,低压涡轮转轴测点振动增强.而风扇转子的振动在低压涡轮不平衡量为3100g·mm时比其他两种不平衡情况下略小,如图14所示,风扇转子转频为驱动转频的三分之一,测点在三种不平衡条件下转频13.3Hz对应的幅值依次为10.37、8.964、10.14.试验所得测点振幅的变化规律与仿真结果一致.

针对上述低压压气机-涡轮转子双盘不平衡量加载参数,另取0～360°之间的七组不平衡相位差进行振动测试试验,经处理测得的数据,得到各测点在其转动频率下的振动幅值变化,如图15、16所示.

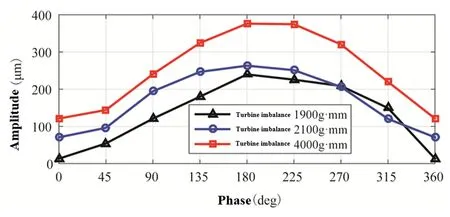
图15 低压涡轮转轴测点的振幅变化Fig.15 Amplitude variation of testing point near low pressure turbine rotor

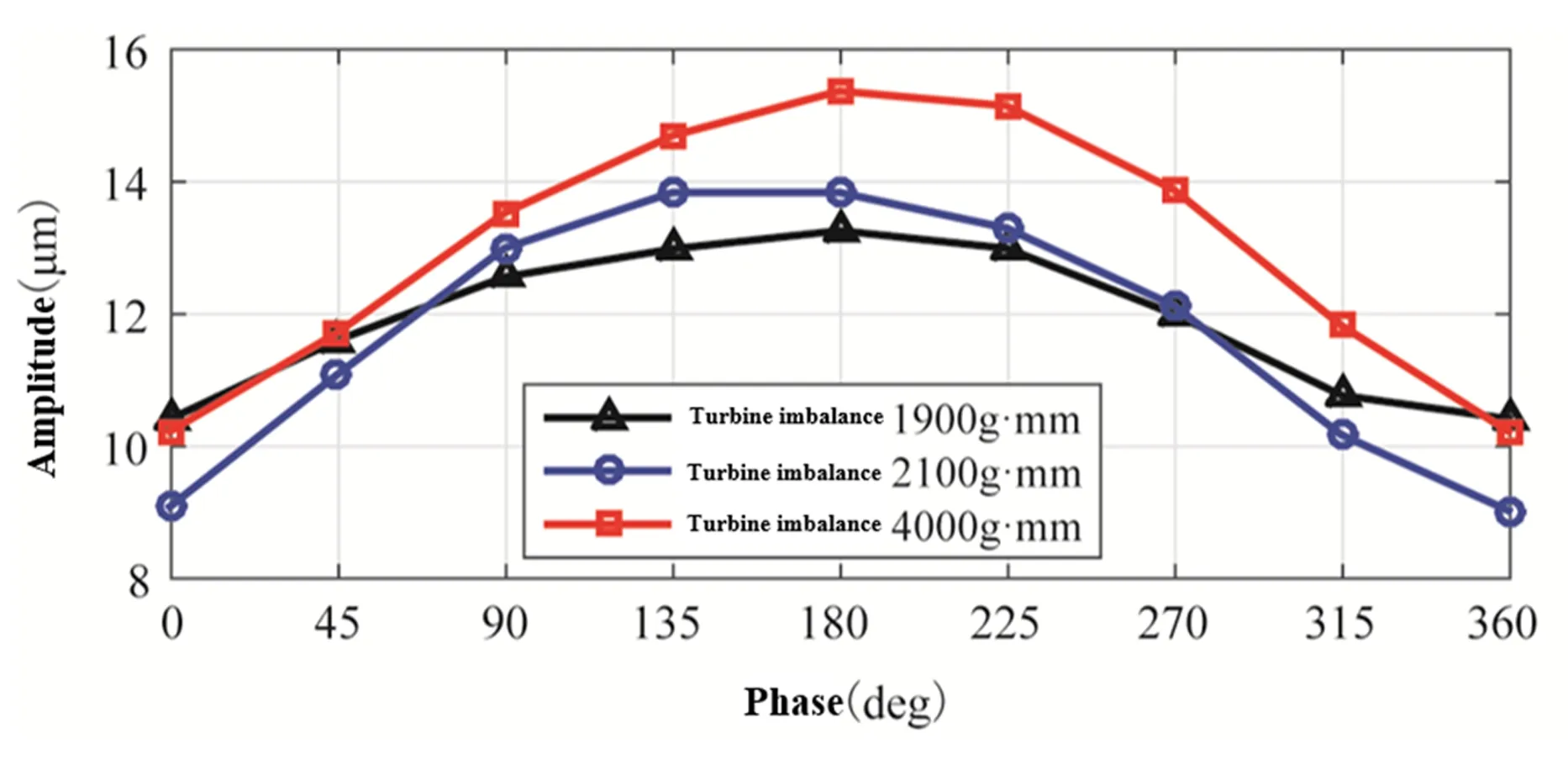
图16 风扇转轴测点的振幅变化Fig.16 Amplitude variation of testing point near fan rotor

由试验结果可知,低压涡轮转轴和风扇转子相应测点的振动随不平衡相位差的变化趋势与仿真结果一致,两测点的振动均在不平衡相位差为180°时最大.但各测点的振幅变化曲线并不完全以相位差180°对称,这是由于试验器安装误差以及传感器与转子试验器处于同一底座上,试验时底座的振动对测点振幅产生影响所致.因此,试验测试所得振动幅值参考意义不大,故未针对与仿真相同的测点进行振幅对比分析.本次试验的测点位置选取主要考虑测点振动信号的避干扰性,旨在验证不平衡量变化对转子振动的影响规律.

5 结论

本文基于试验器基本参数,考虑齿轮副的动态啮合激励,建立具有星型齿轮传动结构的三支点转子系统有限元动力学模型,对转子系统在多种不平衡激励条件下的振动响应特性及齿轮啮合力的变化进行了分析,主要结论如下：

(1)在低压涡轮盘不平衡激励下,低压转子系统各轴段的振幅均随着低压涡轮盘不平衡量增大呈正比增长,且离振源越近,增长率越大.并且在转子不平衡的影响下,齿轮啮合力存在与不平衡激励有关的周期性,以及与啮合频率有关的波动,其中,不平衡对齿轮啮合力的影响较大.

(2)多盘不平衡之间的耦合效应主要体现在低压压气机-涡轮转子双盘不平衡激励下各轴段的振动响应上.当低压压气机和低压涡轮盘不平衡初始相角小于90°时,随不平衡量增大,低压转子系统中除了低压涡轮轴段,其他轴段均存在受双盘不平衡量耦合的影响振动减弱的情况；在同样大小的不平衡条件下,当低压压气机和低压涡轮盘不平衡初始相角为180°时,转子各轴段的振动均达到峰值.此外,在不同的低压压气机-涡轮转子双盘不平衡加载方式下,低压转子系统中环形齿轮和游星齿轮间以及中心齿轮与游星齿轮之间的两组啮合力变化规律与转轴的振动规律相似,其中,与中心齿轮相比,环形齿圈与游星齿轮之间的啮合力更大,且受不平衡相位差的影响更显著.

(3)由于风扇转子的转速仅为低压压气机-涡轮转子转速的三分之一,当转子系统受低压压气机或低压涡轮不平衡激励时,采用风扇配重的方式无法解决转子系统的振动问题.并且在低压涡轮存在不平衡的情况下,低压涡轮轴段的振幅主要取决于涡轮不平衡的大小,受其他不平衡因素的影响很小.