鼠笼局部断裂的刚度特性及其转子动力学特性分析*
2018-03-14温保岗王美令任红军韩清凯
温保岗 王美令 任红军 韩清凯
(1.大连工业大学 机械工程与自动化学院, 大连 116034) (2.大连交通大学 机车车辆工程学院, 大连 116028)(3.辽宁科技大学 机械工程与自动化学院, 鞍山 114051) (4.大连理工大学 机械工程学院, 大连 116024)
引言
现代航空发动机日益向着推重比、大载荷、高转速、高温、高压、高可靠性方向发展,转子-支承系统趋于柔性化.为了使发动机具有先天优良的振动特性,转子动力学比较成熟的做法是采用弹性支承-刚性转子方案,使系统的变形尽量发生在支承上,因此采用弹性支承的设计成为发动机振动特性的重要因素[1,2].其中整体加工的鼠笼式弹性支承结构是比较常用的结构,但鼠笼由于存在较大的应力集中,容易出现疲劳裂纹,甚至笼条断裂,如图1所示,导致发动机振动增加,甚至造成灾难性事故[1,3],因此研究鼠笼疲劳以及疲劳断裂对航空发动机转子系统振动特性影响有着重要意义.
国内外学者对鼠笼支承刚度进行了相关理论及实验分析,冯国全[4,5]进行了鼠笼式弹性支承的优化设计与试验研究,并进行了柔度试验和疲劳应力试验,对鼠笼弹性支承进行了疲劳强度分析.徐方程[7]进行不同结构尺寸的鼠笼弹性支承静刚度测试试验和有限元计算.
弹性支承转子动力学方面,张慈等[7]研究了鼠笼式弹支刚度对转子系统的振动特性影响.张华彪等[8,9]建立了航空发动机的弹支刚性转子系统碰摩的动力学方程,分析了同步全周碰摩的分岔响应以及进行突加不平衡引发碰摩的瞬态响应分析.

图1 鼠笼断裂照片[3]Fig.1 Photo of squirrel-cage with local crack[3]
王美令等[10]建立弹性支承式风扇转子动力学模型,分析其模态以及不平衡响应特性.李兵[11]试验分析了弹性环式挤压油膜阻尼器(ERSFD)-转子系统的弹性环凸台高度、供油条件、滑油温度和不平衡量对转子动力学特性影响.参考文献[3]通过实验研究了弹支笼条根部出现裂纹时引起转子系统振动变化,并采用主动弹支干摩擦阻尼器对鼠笼断裂后的转子振动控制等.实验发现主动弹支干摩擦阻尼器能减小弹支发生局部断裂而增加的振动.目前尚未有鼠笼断裂刚度变化相关研究以及断裂后鼠笼对转子系统动力学特性影响理论分析,因此需要开展鼠笼局部断裂后的刚度变化以及对转子振动影响研究.
本文针对鼠笼断裂引起刚度以及转子振动问题,分别采用理论推导、有限元方法和拟合方法结合提出带局部断裂的鼠笼刚度模型,并基于其支承的两支点转子系统动力学模型进行转子固有特性及振动响应分析,研究鼠笼局部断裂的刚度特性及带有鼠笼局部断裂转子系统固有特性和振动响应的变化规律.
1 鼠笼局部断裂刚度模型建立
1.1 鼠笼局部断裂结构特征
鼠笼疲劳应力多发生在笼条根部,其裂纹多在笼条根部过渡处[3,5].本文以如图2所示的笼条根部断裂的鼠笼为研究对象. 建立固定坐标系为oxyz,其坐标原点o为固定点,位于鼠笼外圈中心点处,x为轴向坐标,y、z为径向坐标.为了确定鼠笼周向断裂位置,引入断裂相位角φi,即断裂笼条位置与安装位置的垂直方向y的夹角,如图2所示,图中ls为笼条有效长度,hs为笼条厚度,bs为笼条宽度,ds为鼠笼外径.
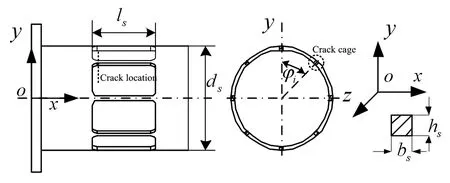
图2 鼠笼断裂结构示意图Fig.2 Squirrel-cage with local crack
1.2 鼠笼局部断裂刚度理论模型
位于相位角φi的第i根笼条受力如图3所示.
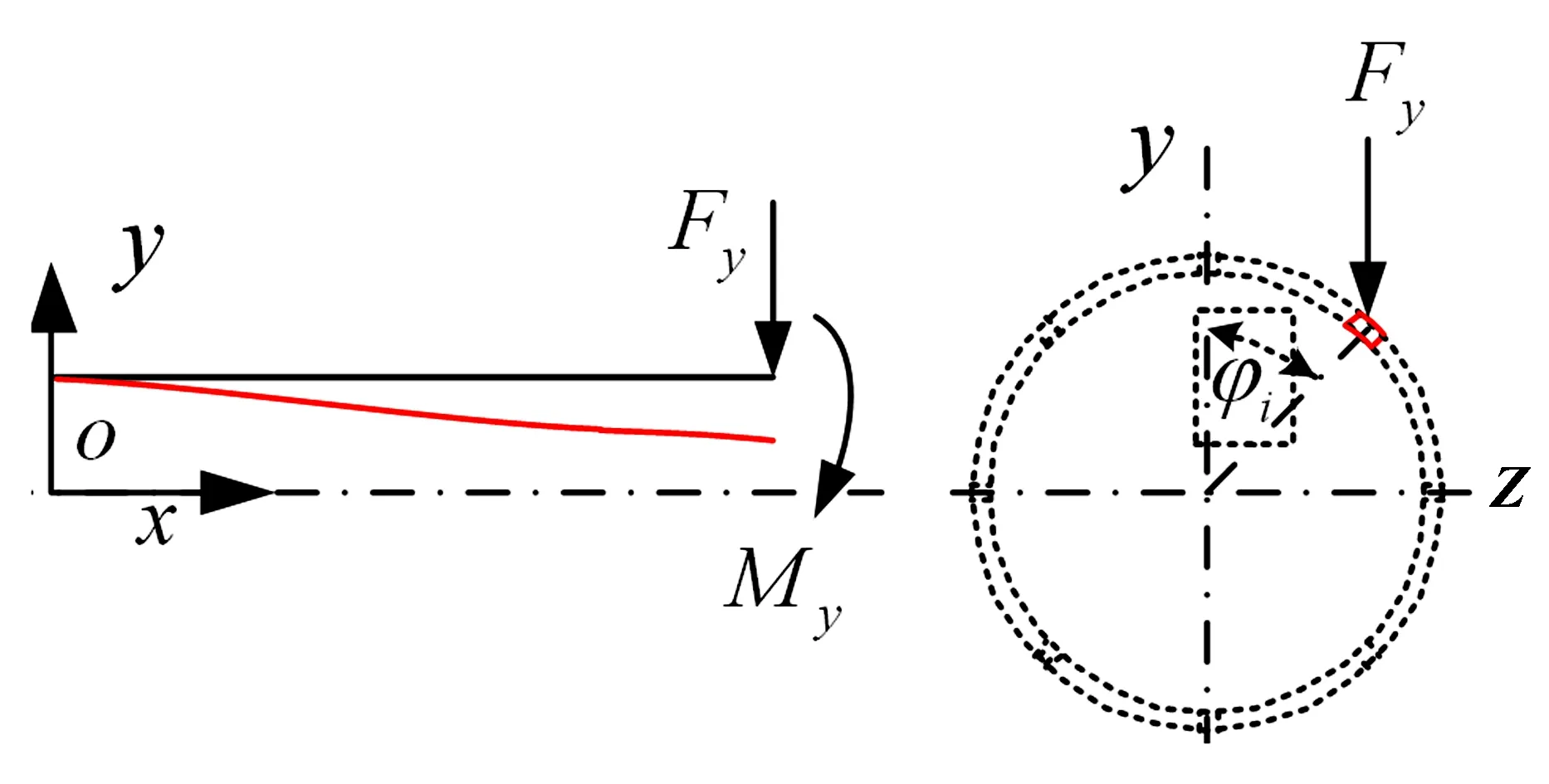
图3 鼠笼第i笼条受力示意图Fig.3 Force on the ith bar of squirrel-cage
通过力学分析,推导得出第i根笼条在水平、垂直方向刚度kiz、kiy为[1,12]:
(1)
假设鼠笼在相位角φi的第i笼条出现断裂,则其水平、垂直方向刚度kz、ky可以表示为:
(2)
式中,kr为正常状态鼠笼刚度.
文献[1,4,6]均指出理论计算鼠笼刚度相对于有限元计算与试验结果偏差较大,下节将通过有限元方法对鼠笼局部断裂刚度进行进一步分析.
1.3 鼠笼局部断裂有限元模型
运用PRO/E软件建立鼠笼的三维模型,其参数如表1所示.并将模型导入ANSYS,模型采用Solid45单元进行自由划分网格,共包含70084个节点,16349个单元,相位角为φi第i根笼条根部在建模时为分离状态.考虑鼠笼通过连接孔与连接座连接安装方式,约束连接孔节点所有自由度. 为了模拟鼠笼与轴承外圈的配合,将鼠笼悬臂端部内圆面上所有节点y和z方向的平移自由度耦合使其一起联动,即各节点在这两个方向的自由度相同,不发生局部变形. 所建立鼠笼有限元模型如图4所示.

表1 鼠笼结构参数及材料特性Table 1 Parameters of the squirrel-cage
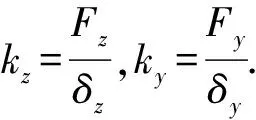
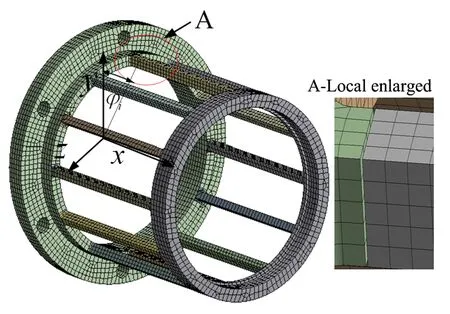
图4 鼠笼有限元模型Fig.4 Finite element model of squirrel-cage with local crack
1.4 鼠笼局部断裂刚度拟合
选取笼条数量n分别为10、12、16、18、20、24鼠笼,断裂相位为φi=0°~180°进行其刚度分析,基于所得的57组有限元计算结果采用最小二乘法拟合方法,获得鼠笼断裂后水平、垂直方向刚度拟合公式(FEF),表示为:
(3)
式中,正常状态鼠笼刚度kr=nEhs2bs2/ls3.
2 鼠笼局部断裂刚度影响分析
因结构形式和尺寸等的不同,鼠笼刚度存在差异,为便于对比不同鼠笼结构尺寸断裂后引起刚度变化,引入无量纲参数“刚度变化率”,ξz、ξy分别表示鼠笼断裂后水平、垂直方向刚度变化率:
(4)
三种模型计算得到鼠笼笼条数量n分别为12、16、18、20在水平、垂直方向刚度变化率ξz、ξy随着断裂相位φi(0~180°)的变化曲线如图5所示.图中,FEA、FEF、AF分别为有限元、拟合公式、理论计算结果.
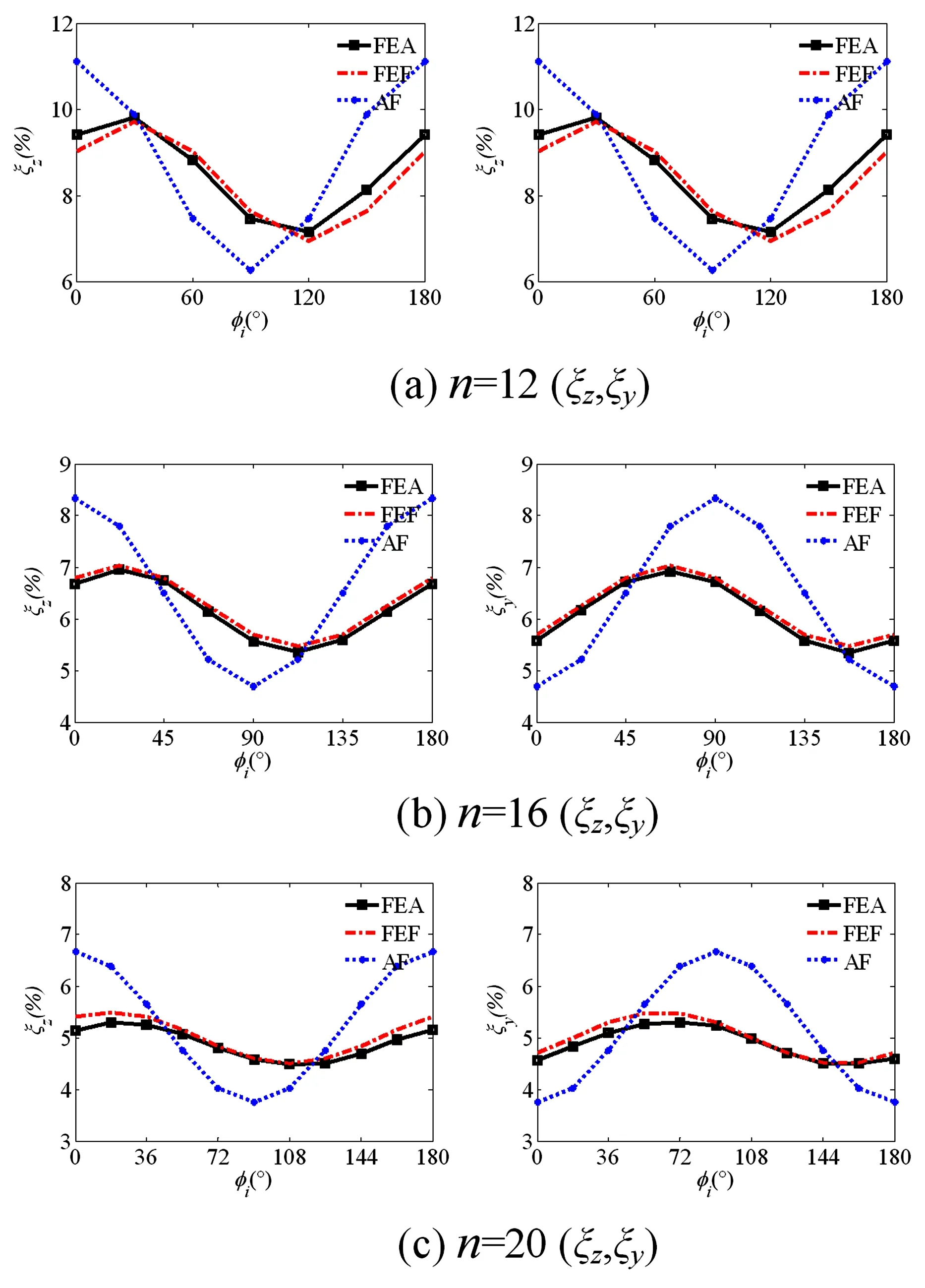
图5 鼠笼刚度变化率ξ与φi关系曲线Fig.5 Relationship between variation coefficient ξ and phase angle φiof squirrel-cage with local crack
由图5可以看出,本文提出的拟合刚度与有限元计算结果有很好的吻合性,理论值与有限元存在一定相位差; 鼠笼断裂后刚度降低且变化率随笼条总数量增加而减小;同时鼠笼在水平、垂直方向刚度降低与断裂相位角为三角函数关系.对比ξz、ξy可以看出,鼠笼局部断裂后水平方向与垂直方向刚度变化率ξz、ξy不同,表明由于鼠笼断裂使其水平与垂直刚度呈现不对称性.
3 带有鼠笼局部断裂的弹支转子系统动力学特性分析
3.1 弹支转子系统动力学模型
针对如图6所示的两支点弹支转子系统[9],建立其4自由度动力学模型:
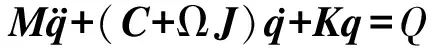
(5)
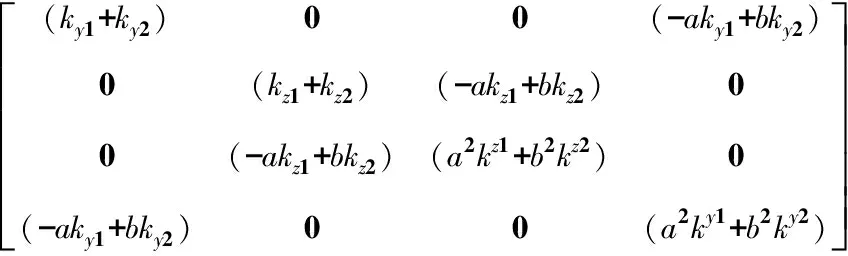
其中,m为转盘质量,其中D为转盘直径,me为不平衡质量,e为不平衡质量距回转中心距离,a为转盘距支点1距离,b为转盘距支点2距离,Jd,Jp分别为圆盘的直径转动惯量和极转动惯量,kz1,ky1,kz2,ky2分别为支点1、2鼠笼水平、垂直支承刚度.
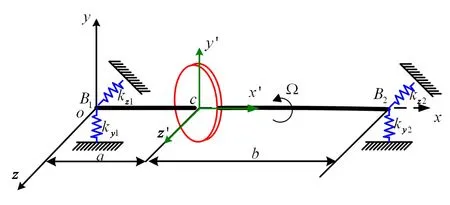
图6 弹性支承转子系统模型Fig.6 Model of rigid rotor system with flexible supports
3.2 算例
针对图6所示的弹支-刚性转子系统,选取支点2处的鼠笼作为断裂鼠笼,鼠笼结构参数和转子模型参数分别如表1-2所示,笼条数n=12,研究鼠笼局部断裂对弹支转子系统振动特性影响.在鼠笼正常状态(Normal)和断裂相位φi分别为0°和90°(φi=0°和φi=90°)时,转子系统的幅频特性曲线,以及在系统亚临界转速(32Hz)和超临界转速(36Hz)时系统的振动响应轴心轨迹分别如图7~8所示.

表2 转子系统的模型参数Table 2 Parameters of the rotor system
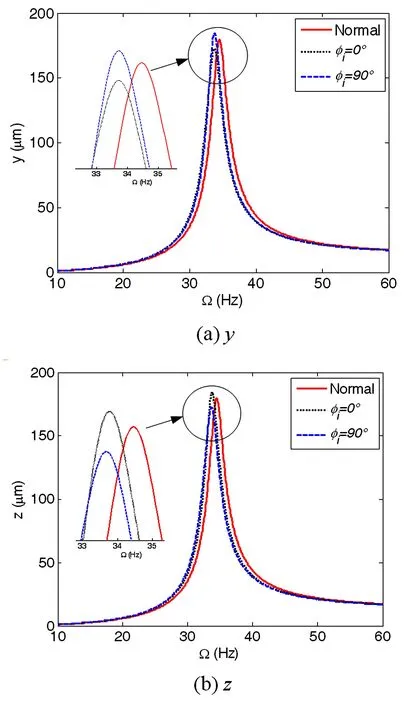
图7 不同鼠笼局部断裂相位下转子系统振动的幅频特性曲线Fig.7 Amplitude-frequency curve for the rotor system under different phase angles φiof local crack in squirrel-cage
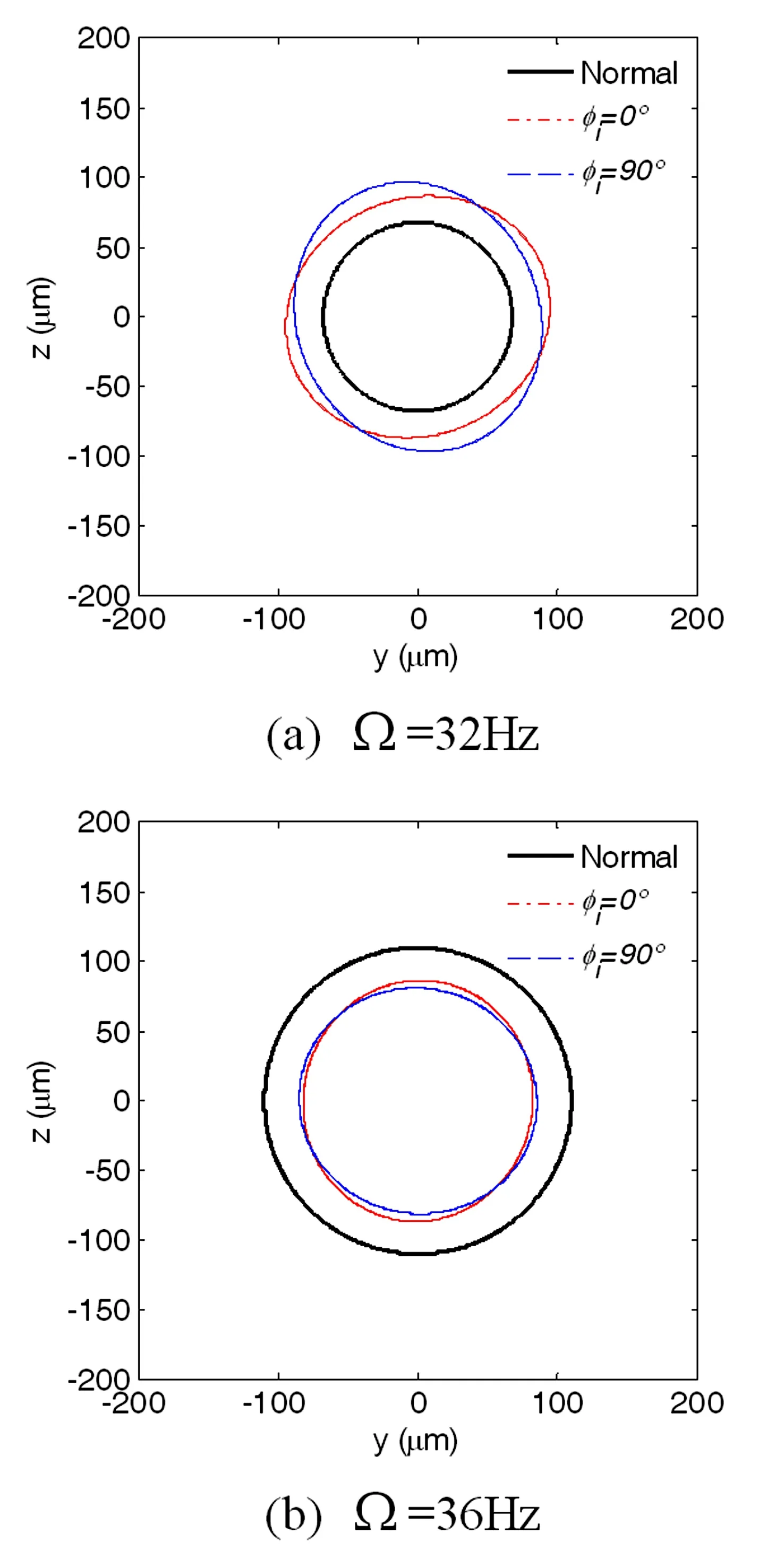
图8 不同鼠笼局部断裂相位下转子系统轴心轨迹图Fig.8 Orbits of the rotor system under different phase angles φiof local crack in squirrel-cage
由上图7~8可以看出,正常状态下,转子系统在垂直方向(y)和水平方向(z)临界转速相同;当鼠笼有局部断裂时,转子系统临界转速有所下降,且在垂直和水平方向上变化不同,这与文献[3]试验测试结果吻合,同时,临界转速的变化受局部断裂相位的影响.此外,转子系统的轴心轨迹由正常状态下的圆形变为椭圆形,且在亚临界转速区振动增大,超临界转速区振动减小,这正是由鼠笼局部断裂引起弹支刚度减小且在水平和垂直方向上不对称引起的.
4 结论
本文开展鼠笼局部断裂刚度特性以及其引起转子动力学特性变化的研究,得出如下结论:
(1)提出了鼠笼局部断裂刚度的理论和拟合经验公式,拟合经验公式与有限元计算结果有很好的吻合性.
(2)带有局部断裂的鼠笼在水平、垂直刚度与其笼条断裂相位角有关.
(3) 鼠笼断裂后其刚度降低,且水平、垂直刚度呈现不对称,这导致鼠笼支承弹支转子系统的临界转速下降,且水平、垂直方向上的振动差异,轴心轨迹呈椭圆形.
