路基沉降对低地板有轨电车动力学性能的影响

蒋建政，孙 宇，郭 宇，陈兆玮，王开云

(西南交通大学 牵引动力国家重点实验室， 成都 610031)

现代有轨电车凭借着绿色环保、载运量大的优点具有广阔的应用前景。与其他轨道交通车辆系统一样，车辆与轨道之间的动态相互作用问题是现代有轨电车中最基本、最重要的动力学问题。同时，由于地下资源的开采等原因，路基沉降问题越来越受到广大学者及工程人员的关注。当有轨电车轨下路基结构发生沉降后，会直接导致轨面几何状态发生改变，并通过轮轨相互作用关系最终影响到有轨电车的正常运行，严重时还会影响到车辆运行安全性。

1 考虑路基沉降的低地板有轨电车轨道垂向耦合动力学模型

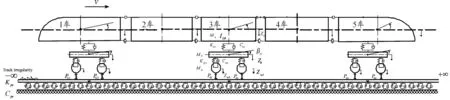
图1 低地板有轨电车轨道垂向耦合动力学模型

1.1 低地板有轨电车车辆模型

与常规有轨电车相比，低地板有轨电车车辆地板距轨面高度低，无需设置站台，因而具有广阔的发展前景。本研究基于五车六轮对结构的低地板有轨电车[10]，见图2。其中：1、5车是动车，并分别安装有动力转向架；2、3、4车为拖车，其中3车安装有转向架。车与车之间通过上下铰和减震器连接。各车之间的下铰采用固定球铰。1、2车，2、3车，4、5车之间的上铰采用转动铰，3、4车的上铰则采用自由铰结构[10]。在本文建立的垂向动力学模型中：固定球铰用以传递大部分的纵向力和垂向力，采用两个纵向和垂向大刚度元件来代替；转动铰允许车体之间的相对转动，模拟为1个纵向刚度元件；而自由铰结构则允许车体之间的转动，端部还起到阻尼作用，用1个纵向刚度元件和1个阻尼器代替。模型中车体、转向架考虑点头和沉浮两个自由度，轮对则只考虑沉浮运动一个自由度。车辆系统动力学方程见式(1)。

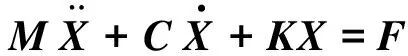
(1)

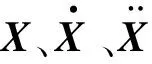
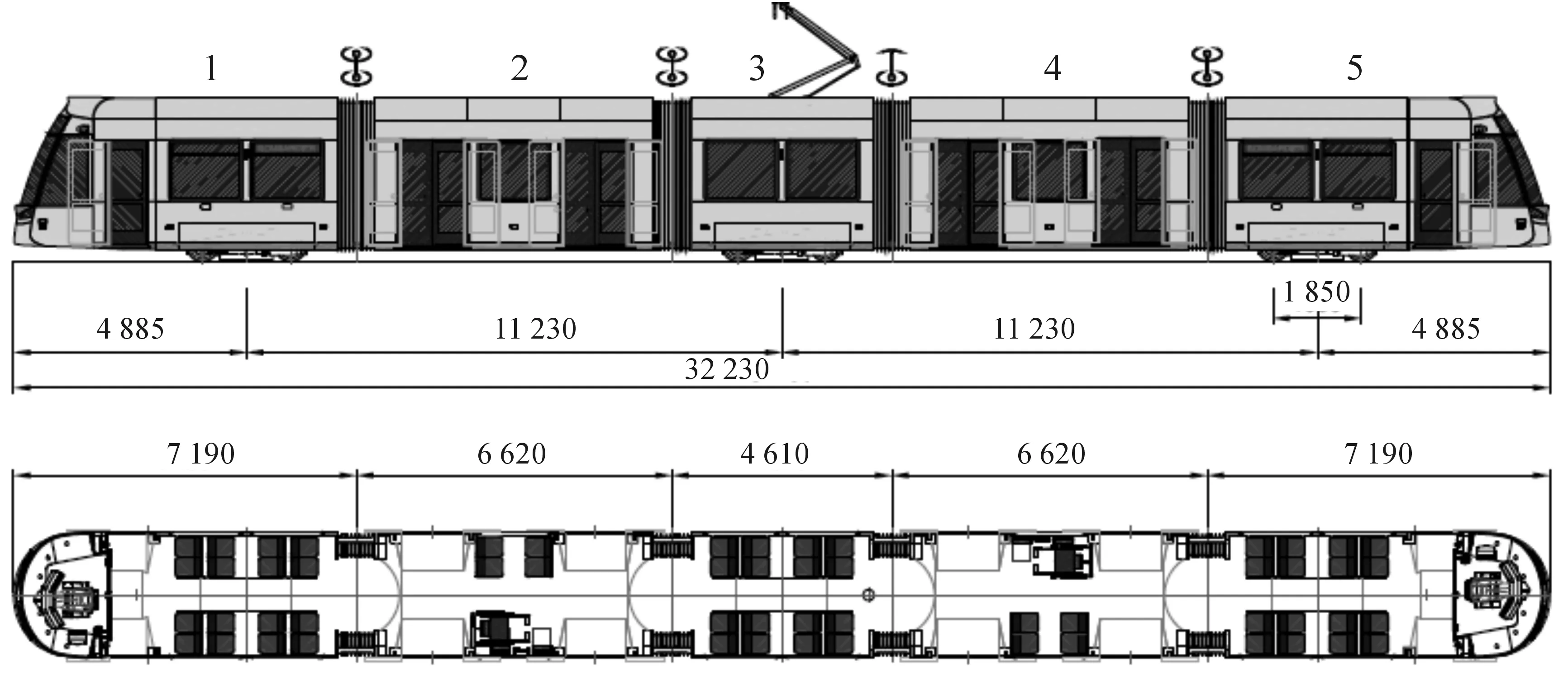
图2 低地板有轨电车结构示意图

1.2 埋入式无砟轨道动力学模型

图3 无砟轨道动力学模型

目前，国内外有轨电车的轨道结构常采用埋入式无砟轨道[11]，因此本文同样采用该形式的无砟轨道。埋入式无砟轨道由钢轨、扣件、路基组成，全部轨道结构埋入道路铺面之下。由于扣件和轨下胶垫主要提供垂向支撑刚度和垂向阻尼用以固定钢轨，故模型中将其等效为垂向刚度元件和垂向阻尼元件。钢轨考虑为有限长欧拉梁模型。该轨道动力学模型见图3，其详细动力学方程见文献[7]。

1.3 轮轨接触模型

轮轨接触模型在整个动力学模型中起到了连接车辆子模型和轨道子模型的作用。本文使用赫兹非线性接触理论[7]计算轮轨间的垂向作用力p(t)。当轮轨脱离时轮轨垂向作用力为0，见式(2)。

(2)

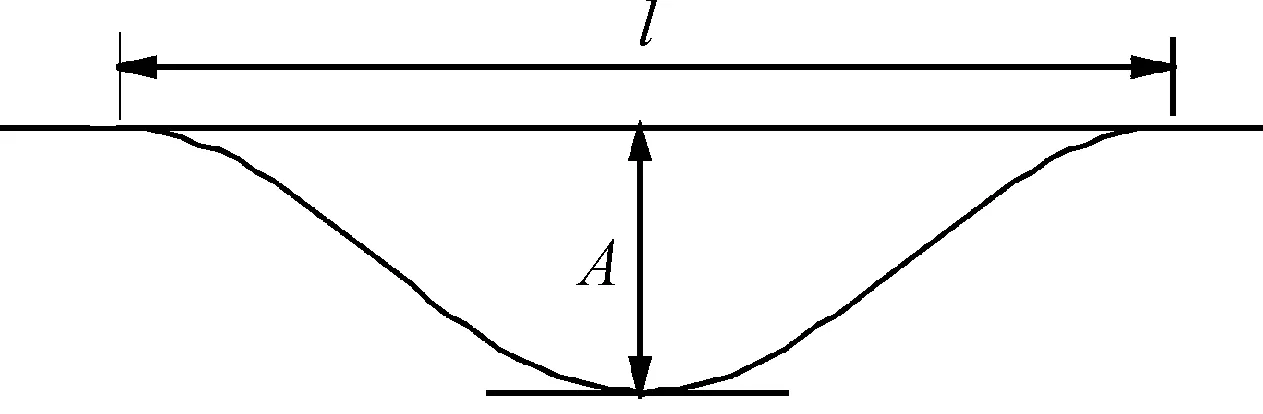
图4 路基不均匀沉降模型

式中：Zwj(t)为第j位车轮在t时刻的垂向位移；Zr(xwj,t)为t时刻第j位车轮下钢轨的垂向位移；Z0j(t)为轮轨界面的垂向位移不平顺；Zc(xwj)为距原点x处路基沉降值。

1.4 路基不均匀沉降模型

路基不均匀沉降是指沿着轨道纵向分布的垂向不均匀变形。本文使用目前研究中常见的下凹型余弦波模拟路基不均匀沉降[3]，直接将路基沉降变形等价为轨面高低不平顺[6]，见式(3)。式中：l代表沉降波长；A代表沉降幅值即沉降波深；x代表沉降处距原点的距离。图4是余弦型路基沉降模型。

(3)

1.5 数值积分方法

(4)

2 低地板有轨电车通过路基沉降区域时的动力学响应

为了更突出地展示路基沉降对低地板有轨电车系统产生的影响，本文分析时忽略了轨道随机不平顺的影响。本节计算了有轨电车以70 km/h的速度通过30 m波长、不同波深路基沉降区域时的动力学响应，并选取了对路基沉降较敏感的1位车体垂向振动加速度，1位轮对轮轨垂向力和钢轨垂向位移3个动力学参量进行分析，用以定性说明路基沉降对有轨电车系统动力性能的影响。

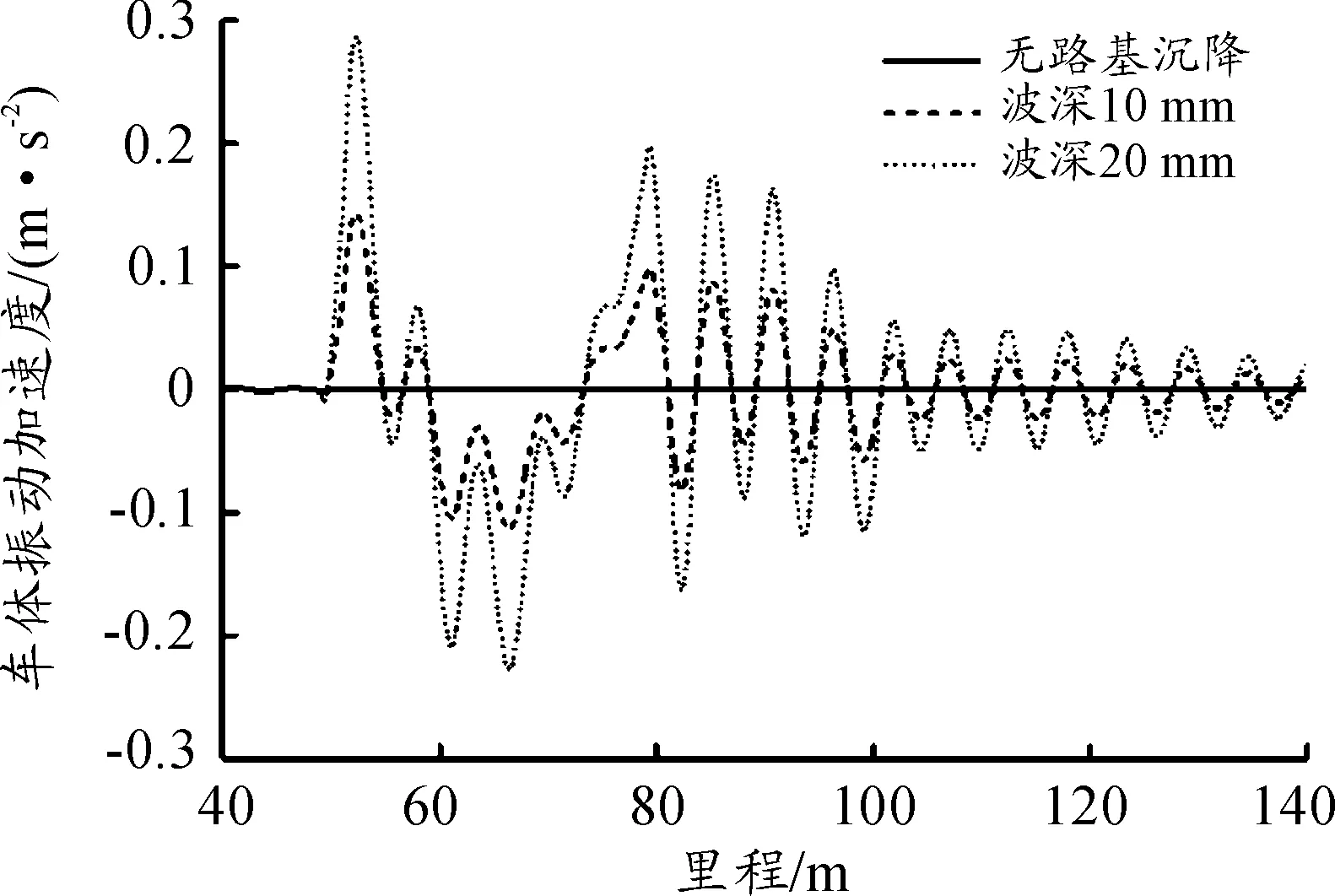
图5 1位车体垂向振动加速度

图5给出了低地板有轨电车通过该沉降区域时1位车体垂向振动加速度的时间响应曲线。由图5可以得到：1位车体垂向振动加速度在通过沉降区域时振荡剧烈，通过沉降区域后衰减缓慢，并随着波深增加，振动加速度幅值也有明显增加。

图6给出了低地板有轨电车通过该沉降区域时1位轮对轮轨垂向力的时间响应曲线。从图6可以得知：通过沉降区域时，1位轮对出现了明显的先减载后增载的现象，其幅值随波深的增加而增加。

图7给出了低地板有轨电车通过路基沉降段时轮轨接触点处钢轨垂向位移的时程曲线。由图7可以得知：钢轨的垂向位移变化趋势与轮轨垂向力变化趋势保持一致。

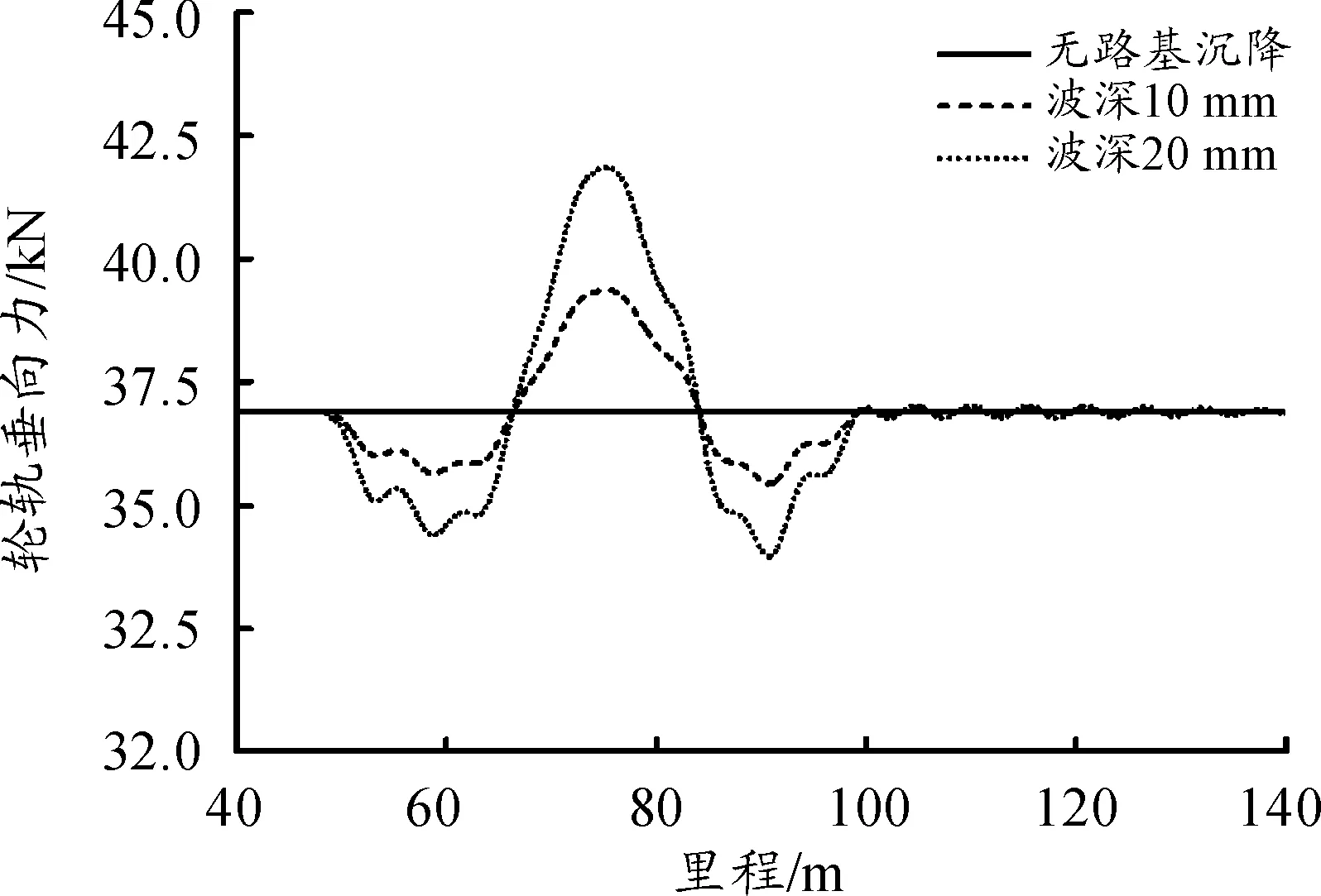
图6 1位轮对轮轨垂向力

车体的振动加速度、其他位轮对的轮轨垂向力和钢轨位移的时程变化趋势与图5～7中的结果类似，由此可以知道路基沉降会加剧有轨电车的振动。

3 路基沉降参数对低地板有轨电车的动力学性能影响

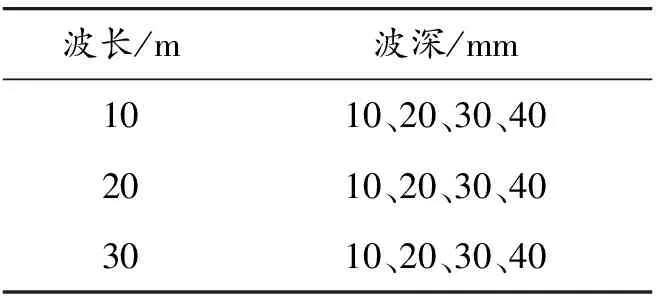
表1 计算工况统计

3.1 路基沉降波长对动力学性能的影响

图8～10给出了低地板有轨电车以不同速度通过20 mm波深、不同波长路基沉降段时1位车体垂向振动加速度、1位轮对轮轨垂向力、钢轨垂向位移的最大值。

图8给出了1位车体在通过路基沉降段时车体垂向加速度最大值统计图。由图8可知：沉降波长和行车速度会影响1位车体的垂向振动。波长一定时，随着行车速度的提升，车辆振动会有明显的增加；当行车速度一定时，减少沉降波长会加剧车辆垂向振动。另外，随着波长的减小，车体垂向加速度超出了既有标准中规定的数值[12]，也证明了路基沉降对低地板有轨电车系统动力学响应影响较大，在工程实践中应注意轨道的养护维修。

图9、10分别是低地板有轨电车通过不同波长沉降段时1位轮对的轮轨垂向力和钢轨垂向位移。通过沉降路段时，行车速度和沉降波长都会影响轮轨垂向力和钢轨垂向位移。增加行车速度会加剧轮轨动作用力，减小沉降波长也会加剧轮轨间的动作用力，当波长减小至10 m时，轮轨作用力达到最大。钢轨垂向位移变形与轮轨动作用力的变化保持一致，车辆运行速度达到70 km/h时，响应增长明显。

图8 1位车体垂向振动加速度

3.2 路基沉降波深对动力学性能的影响

图11～13给出了低地板有轨电车以不同速度通过10 m波长、不同波深沉降段的动力学响应。图11是1位车体通过沉降路段时车体垂向振动加速度统计。由图11可知：增加沉降波深和行车速度都会加剧车辆的垂向振动。行车速度对车体垂向振动加速度的影响程度要大于波深对车体垂向振动加速度的影响。

图12、13分别给出了1位轮对轮轨垂向力以及钢轨垂向位移。二者变化趋势一致，行车速度和沉降波深都会影响轮轨动力响应。随着沉降波深的增大，轮轨垂向力和钢轨垂向位移会近似呈线性增大。增加行车速度时轮轨垂向力和钢轨垂向位移也会随之增大，行车速度达到70 km/h时，增长明显。

图10 钢轨最大垂向位移

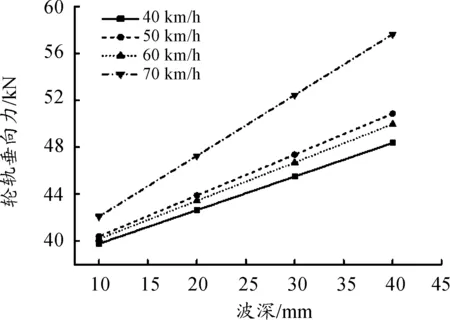
图12 1位轮对最大轮轨垂向力

4 结束语

[1] 陈兆玮，孙宇，翟婉明.高速铁路路基沉降与钢轨变形的映射关系(Ⅱ)：纵连板式无砟轨道系统[J].中国科学：技术科学，2014，44(7)：778-785.

[2] 陈兆玮，孙宇，翟婉明.高速铁路路基沉降与钢轨变形的映射关系(Ⅰ)：单元板式无砟轨道系统[J].中国科学：技术科学，2014，44(7)：770-777.

[3] 郭宇，高建敏，孙宇，等.路基沉降与双块式无砟轨道轨面几何变形的映射关系[J].铁道学报，2016，38(9)：93-99.

[4] 徐庆元，李斌，周志辉.CRTS-1型板式无砟轨道线路路基不均匀沉降限值研究[J].中国铁道科学，2012，33(2)：1-5.

[5] 蔡小培，刘薇，王璞，等.地面沉降对路基上双块式无砟轨道平顺性的影响[J].工程力学，2014，31(9)：160-165.

[6] 韩义涛，姚力.基础沉降对土路基上板式轨道动力性能影响分析[J].铁道工程学报，2007(10)：28-31.

[7] 翟婉明.车辆-轨道耦合动力学[M].4版.北京:科学出版社，2015.

[8] 肖威.路基不均匀沉降对CRTS3型板式轨道动力学特性的影响[D].成都：西南交通大学，2015.

[9] CHEN Zhaowei，ZHAI Wanming，CAI Chengbiao，et al.Safety threshold of high-speed railway pier settlement based on train-track-bridge dynamic interaction[J].Science China-Technological Sciences，2015，58(2):202-210.

[10] 冯建龙，王开云，翟婉明.100%低地板轻轨列车焊缝区不平顺动力学响应分析[J].西南科技大学学报，2015，30(4)：10-14.

[11] 胥燕君，林红松，王建,等.现代有轨电车轨道结构综述[J].铁道标准设计，2014，58(7)：59-62.

[12] 铁运[2008]28号.高速动车组整车试验规范[S].