一种基于驾驶员制动行为的车辆主动避撞模型研究

刘志强，张春雷，倪 婕，朱伟达

(江苏大学 汽车与交通工程学院， 江苏 镇江 212013)

国内外学者提出了固定距离法、驾驶员预估模法等安全距离模型[3-4]和碰撞时间模型(time to collision，TTC)以实现主动避撞功能，但由于安全距离模型公路利用率低、参数获取困难等原因并未得到推广[5]。碰撞时间模型未考虑两车同速行驶时的危险状态，存在理论缺陷，且未考虑驾驶员因素，不能反映驾驶员避撞特性，因此接受度不高。

基于此，本文通过在驾驶模拟仪上获得的10名驾驶员的多组跟车试验数据，采用PCA分析法确定的4个相关的车辆状态参数来描述驾驶员制动行为，建立符合驾驶员跟车习惯的制动行为模型(driver’s braking behavior，DBB)。在此基础上完成DDB模型和TTC模型的仿真分析。最后通过模拟驾驶仪对DBB模型和TTC模型进行试验分析。

1 试验数据采集及分析

1.1 驾驶参数数据采集

本文试验数据采集平台采用的是基于虚拟交通环境的交通安全研究实验平台——江苏大学“QJ-4B1型6自由度模拟驾驶器”。本研究试验场景为双向4车道的城市道路，初始两车相距18 m，考虑了前导车加速、匀速、减速3种行驶状态，符合实际交通环境。图1为前导车加速度曲线。

在正式开始试验前允许每位试验者先按照设计场景进行几次预试验，以便被试人员熟悉驾驶仪的操作。当被试者适应虚拟驾驶场景后开始试验，每位试验人员的场景都是一样的，以保证所采集的数据的通用性和可对比性。另外，由于模拟驾驶仪对前导车加速度信息设定的局限性导致前导车的速度曲线过于理想化，与实际道路行驶过程中车辆运行状态的复杂多变性不符，所以本文首先进行了一组预试验，即以图1所示的前导车加速度为试验场景，采集后车运行速度值，结果见图2。在正式试验过程中以预试验时后车的速度值作为前导车的速度信息。

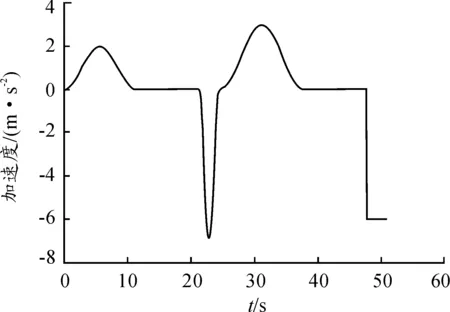
图1 前导车加速度曲线

通过查阅文献及相关资料可发现[6]：与跟驰有关的参数包括前车加速度a1、相对距离d、相对速度Δv、碰撞时间倒数TTCi、车头时距THW、前车速度v1、自车速度v2。通过对某次试验采集的在驾驶员采取制动措施前2 s内参数的变化进行分析(见图3)，从数据变化上可以认为驾驶员制动行为是受到这些外界信息变化的刺激而产生的。所以，本文采集的试验数据为：① 跟驰制动行为数据，包括相对距离d、车头时距THW、碰撞时间倒数TTCi、自车加速度a2、自车速度v2、前车加速度a1、相对速度Δv；② 制动意图数据，包括制动踏板开度、制动踏板开度变化率。THW、TTCi是通过采集的车速、距离参数运算得到。

车头时距(THW)计算公式为

TWH=D/V1

(1)

碰撞时间倒数(TTCi)计算公式为：

6）电气设备：主要由供配电部分、液压动力部分、控制部分、照明部分、信号显示及安全信号保护等部分组成。移动式电站能满足堆料装置和配套进料装置的供电，堆料装置自身配置移动式电站，使得堆料装置应用更加自如，无论是否有岸电，或岸电的频率电压等级如何，堆料装置都能独立工作。

TTCi=1/TTC=ΔV/D

(2)

图4是后车速度、加速度数据采集片段。图5为自车速度、加速度数据采集片段。

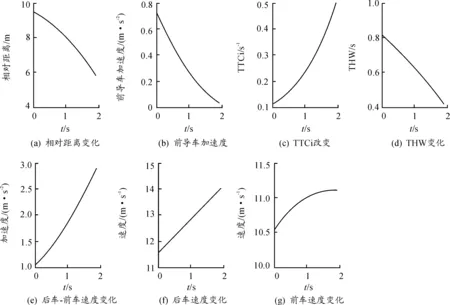
图3 制动前2 s参数变化

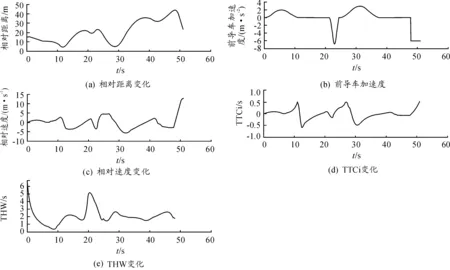
图4 后车速度、加速度数据采集片段

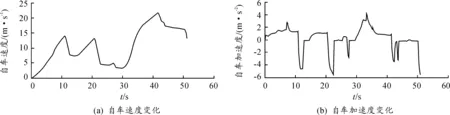
图5 自车速度、加速度数据采集片段

1.2 基于PCA的试验数据分析

本文基于PCA理论对试验数据进行分析，以确定试验采集参数对驾驶员制动行为特性的贡献率。设定试验采集到的前车加速度a1、相对距离d、相对速度Δv、碰撞时间倒数TTCi、车头时距THW、前车速度v1、自车速度v2依次为X1,X2,…,X7，对其进行标准化处理：

(3)

式中：μi为Xi的均值；σii为Xi的标准差；Zi为标准化后的试验参数。

任意两主成分Xi、Xj之间的协方差为

(4)

令Σ表示7个变量的协方差矩阵，则

(5)

为避免因变量间所采用的量纲不同而引起的协方差数值上的变化所带来的弊端，用相关系数来衡量协方差。Xi与Xj之间的相关系数为

(6)

标准化矩阵Z=[Z1,Z2,…,Z7]的第i个主成分Yi表达式为

(7)

(8)

主成分Xi的方差对总方差的贡献率为

(9)

式中λi为主成分Xi的特征值，即该主成分的方差。

本文基于WEKA[7]软件平台对数据进行PCA处理，试验样本的数据分布见图6。经计算，贡献率前4的参数的累计贡献率及特征值如表1所示。

由以上结果可知：本文选取TTCi、Δv、a1、d这4个主要参数即可建立驾驶员制动行为模型。

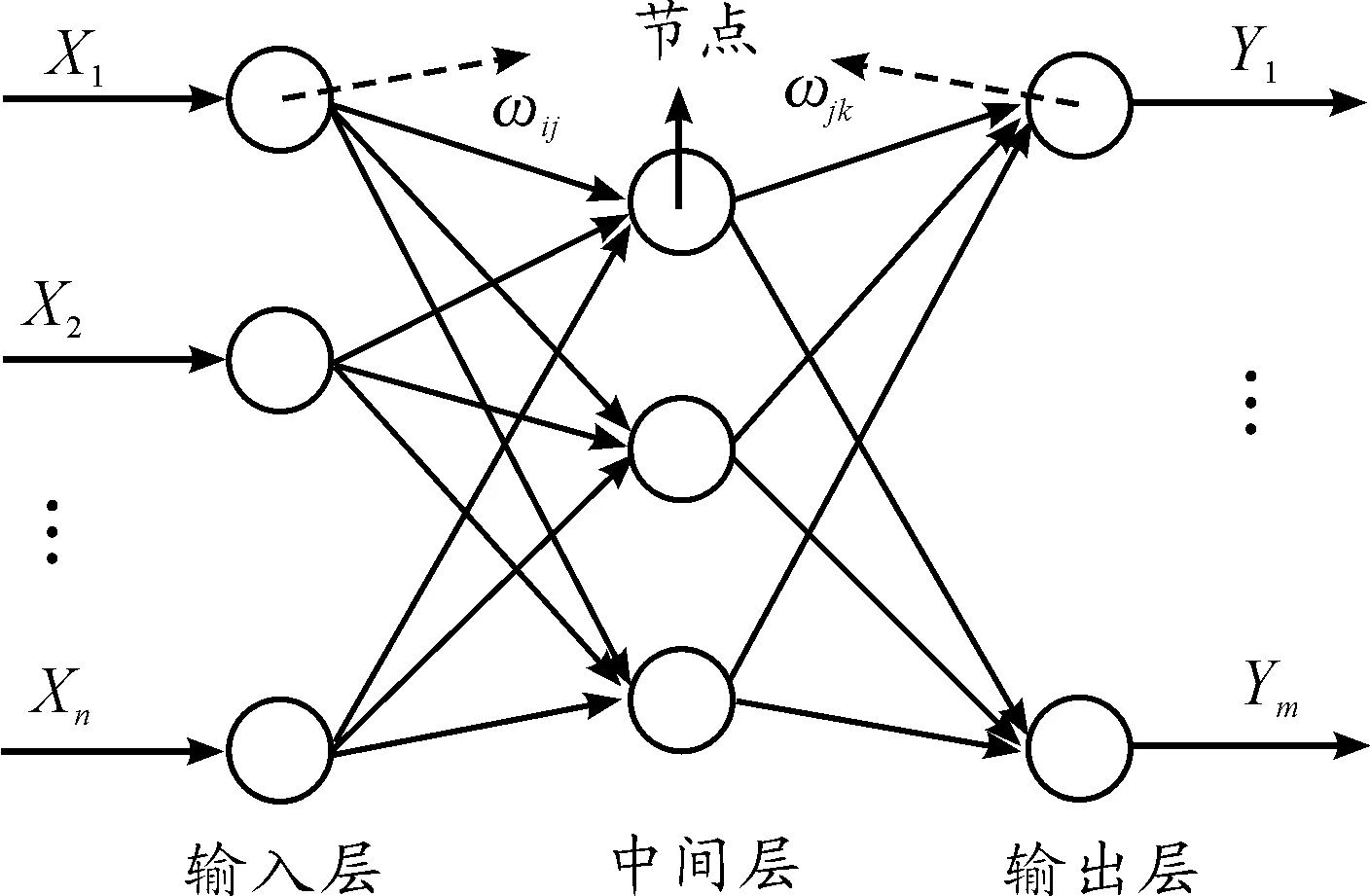
图7 BP神经网络模型的拓扑结构

2 驾驶员制动行为模型

2.1 BP神经网络理论

BP(back propagation)神经网络是由Rumelhart和McMelland领导的科学小组于1986年提出的一种多层前馈型神经网络[8-9]。在预测过程中，该神经网络通过将信号向前方传递、误差向后方传递的方式不断调整神经网络结构的权值和阈值，使得网络预测结果的误差平方和尽可能最小[9]。图7为BP神经网络的拓扑结构，其中：X1、X2、…、Xn为BP神经网络模型的输入值；Y1、Y2、…、Ym为预测值；ωij、ωjk为BP神经网的权值。

2.2 基于BP神经网络的驾驶员制动行为模型

表2 训练结果

根据Kolmogorov学者的研究发现：3层结构的神经网络在中间层节点数充足时具有任意R上[0,1]到R的映射能力和组织、适应能力[10]。因此，本文选用4-n-1三层结构。输入层4个节点为前车加速度a1、相对距离d、相对速度Δv、碰撞时间倒数TTCi，输出层1个节点为后车加速度aego。

为了确定模型的最佳中间层节点数，对不同节点数下模型的预测效果进行了相互对比。神经网络其他初始参数设置为：学习率0.05，动量常数0.9，最大训练次数1 500。表2为120 s循环训练时长下的最佳训练进度和最短训练时间。

由表2可知：中间层节点数为7和13时训练结果最好，其预测结果如图8所示。由图8可以看出：中间层节点数为13时本预测模型的训练精度最高。因此，本文模型的中间层节点数为13。

图9为对模型进行预测训练的样本点分布和误差曲线。图10为训练模型的BP神经网络回归结果。由图10可以看出：该模型在1 600次迭代时误差为0.001，样本的回归性和预测性较好。

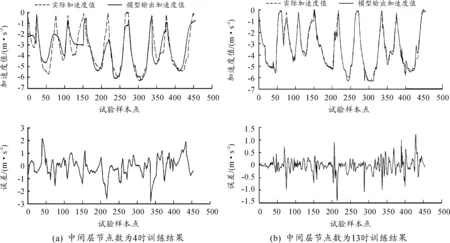
图8 中间层节点数为7和13时的模型训练结果

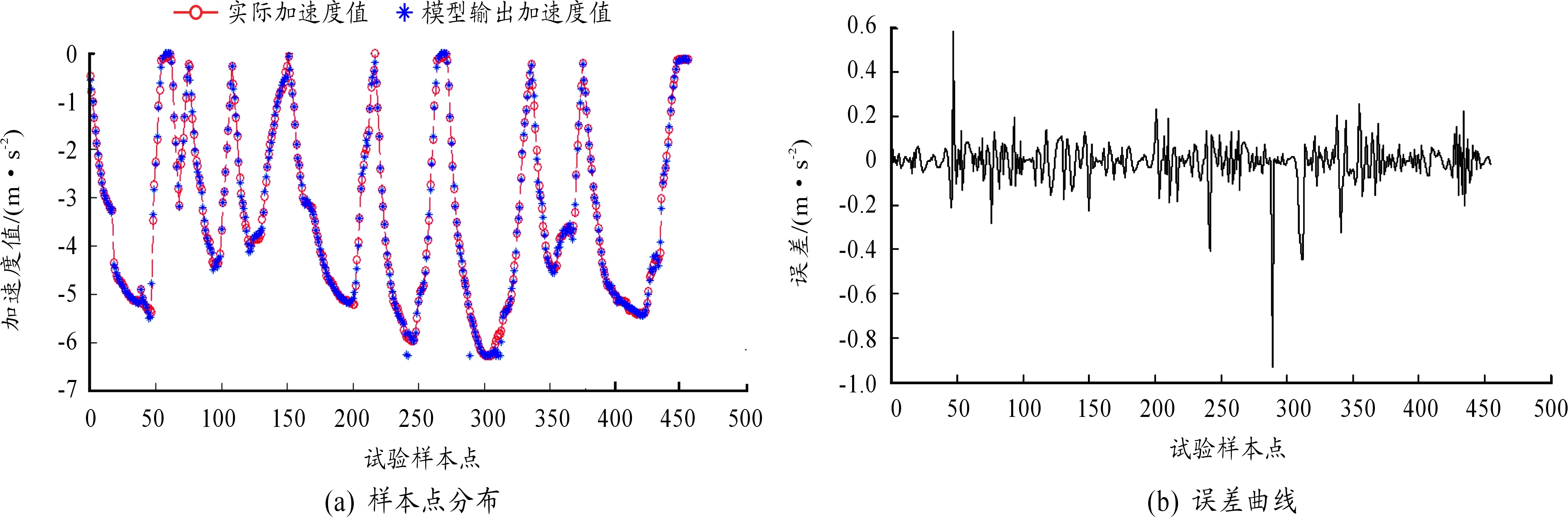
图9 BP神经网络训练结果

2.3 模型验证

为了检验驾驶人制动行为模型的有效性和通用性，重新选取240组未参与建模的试验数据进行模型验证。通过检验样本的预测值与样本实际值的吻合度来检验制动行为模型的有效性。图11为本次模型检测结果，可以看出本次的240组检测样本中只有3组数据检测样本误差绝对值超过1。图12为试验车辆加速度真值与基于BP神经网络的制动行为模型预测值的变化情况，图中试验车加速度真值与本文模型的预测值能较好匹配。因此，本文驾驶人制动行为模型对于驾驶人制动行为的预测较为准确，表明该模型是有效的。

图10 BP神经网络回归结果

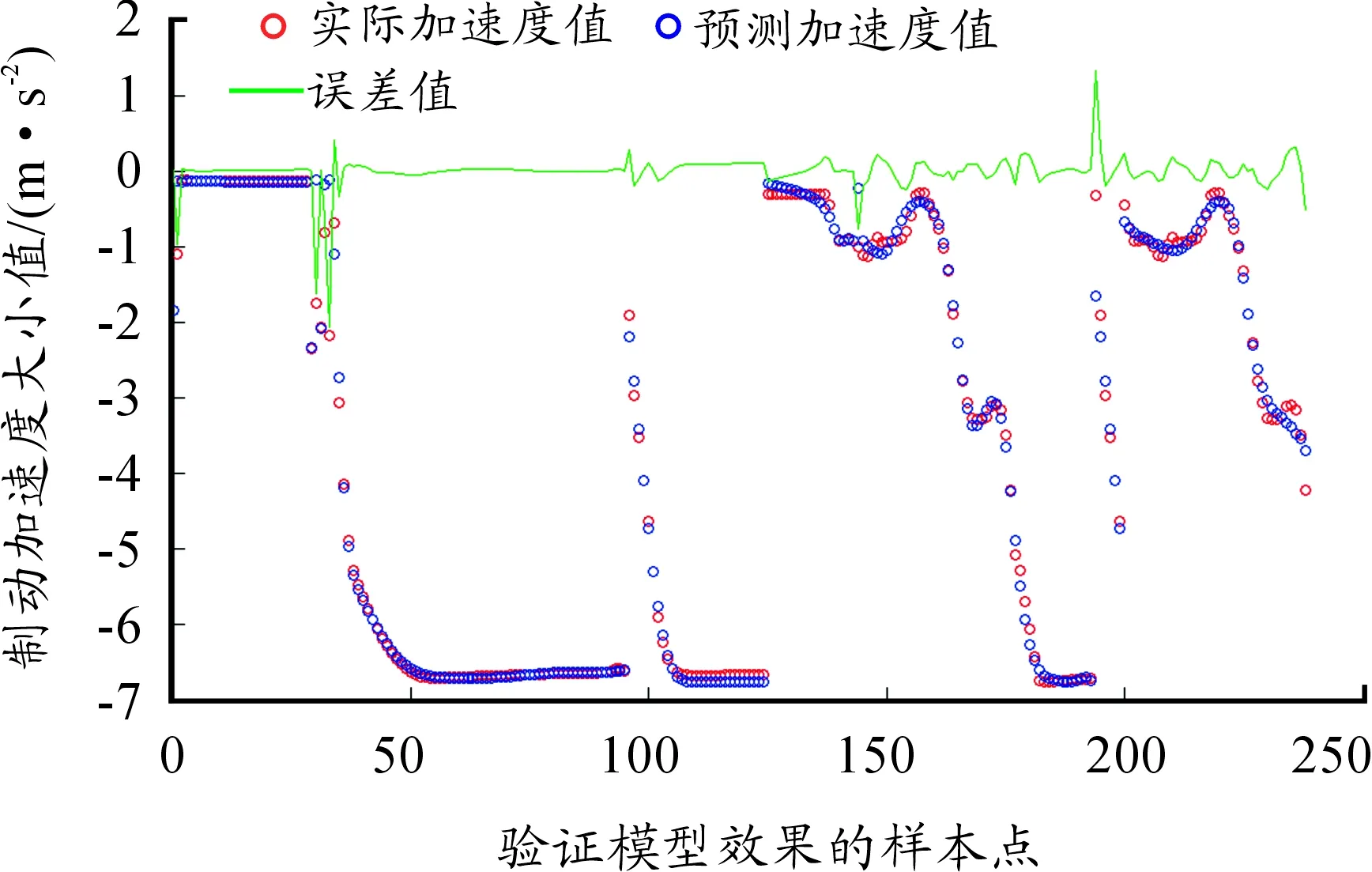
图11 制动行为模型检测结果

图12试验车加速度真值与预测值

3 结论

本文通过仿真和试验证实了DBB模型的有效性和通用性，表明该模型能准确预测车辆的加速度值。

1) 该模型在1 600次迭代时误差已经达到0.001，样本的回归性和预测性能较好。

2) 对试验采集未参与建模的240组检测样本进行模型验证，只有3组数据检测样本误差绝对值超过1，说明该模型具有有效性和通用性。

3) 采集到的试验车辆加速度真值与应用该模型预测得到的预测加速度值基本吻合。

[1] 李瑾南，万娟，李凯，等.智能交通系统发展及趋势分析[J].工业技术创新，2014，1(3)：374-380.

[2] 王国锋，宋鹏飞，张蕴灵.智能交通系统发展与展望[J].公路，2012(5)：217-222.

[3] HIRAOKA T，TANAKA M，KUMAMOTO H，et al.Collision risk evaluation index based on deceleration for collision avoidance (first report)-Proposal of a new index to evaluate collision risk against forward obstacles[J].Review of Automotive Engineering，2009，30(4):429-437.

[4] 武黎明，方正鹏.浅谈智能交通对道路交通安全的作用[J].公路交通科技，2014(3)：276-278.

[5] 吴涛.考虑驾驶者避撞行为特性的汽车前方防碰撞系统研究[D].长春：吉林大学，2014.

[6] TAKADA S，HIRAOKA T，KAWAKAMI H.Effectiveness of forward obstacles collision warning system based on deceleration for collision avoidance[J].IET Intelligent Transport Systems，2014，8(6):570-579.

[7] 威滕.数据挖掘= Data Mining:Practical Machine Learning Tools and Techniques [M].2版.北京：机械工业出版社，2005.

[8] The improvements of BP neural network learning algorithm[C]//WCCC-ICSP 2000，5th International Conference on.USA:IEEE，2000:1647-1649.

[9] WU W，FENG G，LI Z，et al.Deterministic convergence of an online gradient method for BP neural networks[J].IEEE Transactions on Neural Networks，2005，16(3):533-540.

[10] 朱凯，王正林.精通 MATLAB 神经网络[M].北京：电子工业出版社，2010.