应用二次指数平滑法的光栅信号细分方法研究

李 钢，陈自然，田 伟，赵 建，李 云

(1.重庆理工大学 机械检测技术与装备教育部工程研究中心，时栅传感及先进检测技术重庆市重点实验室， 重庆 400054；2.五凌电力有限公司， 长沙 410004)

光栅传感器由于具有容易实现自动化与数字化的优势，在自动化测量领域应用十分广泛，所以提高光栅传感器的测量精度，无论是在机械加工还是在国防建设方面都具有重大意义。而分辨率是评价光栅传感器性能的重要指标，传统的光栅传感器的分辨率取决于光栅栅距刻划的密集程度。但由于高精密的栅线刻划能力对制造设备以及相关技术的要求很高，因此无法得到大规模的普及，并且栅线密度过大会给光栅传感器的动态性能带来影响。因此，国内外学者将研究焦点由栅线的高密度刻划转移到了对光栅输出原始信号的辅助细分[1-5]。由于半导体技术和信息化产业的发展，嵌入式系统也逐渐运用到了光栅细分领域。文献[6-8] 提出一种采用高速 DSP 对光栅信号进行数字细分的方法,并应用数字滤波以提高细分精度。文献[9-10]提出一种基于FPGA 的光栅信号细分及辨向方法,并设计了一种基于幅值采样细分方法的电路，最终实现对光栅信号的细分和辨向。文献[11]提出了基于智能数字锁相技术的光栅细分方法，并研究了该方法中光栅跟踪速度与细分数的关系，缩短了锁相时间，提高了跟踪速度。但上述文献提到的细分方法最终的细分效果仍依赖于光栅传感器输出原始信号的信号质量,特别是对正弦性和正交性有较高的要求。本文提出一种应用指数平滑预测算法的光栅信号细分方法，将对空间的测量转化为对时间的预测，是一种细分结果与光栅输出信号的正弦性与正交性无关的方法。

1 光栅信号预测细分原理

在物体运动过程中，空间位置与运动时间存在着一一对应的关系，如果物体的运动轨迹固定，那么对空间位置的测量可以转化为对时间的测量，对于栅式传感器，刻划在传感器上的栅距类似于位置坐标。当传感器运动时，每一时刻都对应着一个“坐标”。但“坐标”的精度受工艺制造水平的限制，而时间的精度可以精确到很小。这种将时空转换的思路运用到光栅传感器的辅助细分中的方法,能突破光栅传感器在制造工艺上的局限，实现光栅的高精度细分[12-16]。

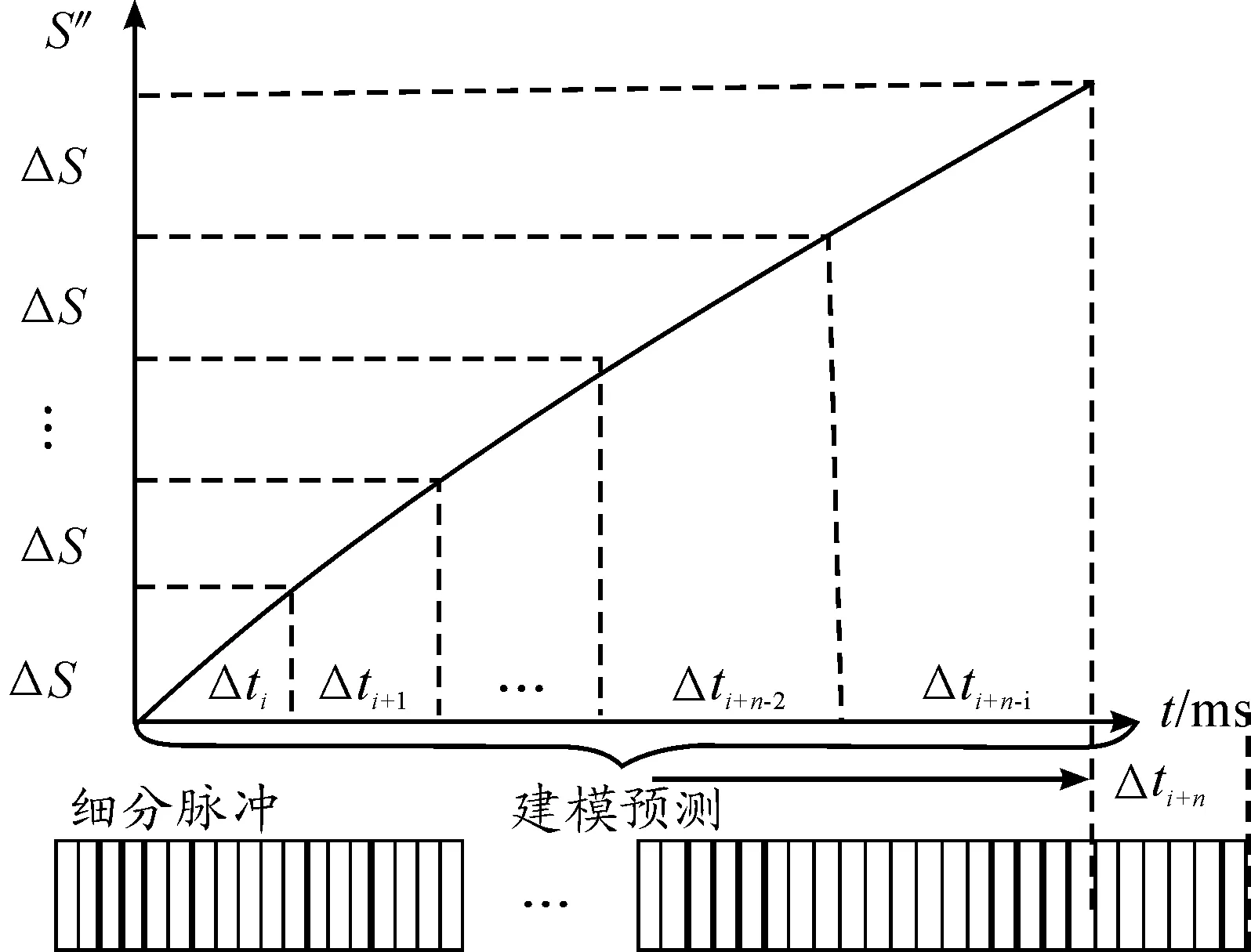
图1 光栅预测细分模型

图1所示为光栅预测细分模型，光栅单位栅距的大小是固定的ΔS，而经过每个栅距的时间与光栅运动速度相关,通过对历史单位栅距的运行时间Δti,Δti+1，…，Δti+n-1分析并建立数学模型，预测经过下一个栅距的时间Δti+n，在Δti+n内，根据设定好的细分倍数，嵌入式微处理器即可输出相对应的细分脉冲，实现光栅传感器的预测软细分。

2 光栅细分算法研究

光栅传感器在运动的过程中，因为惯性的存在，使得光栅运动具有一定的稳定性，运动速度不会发生骤变，因此，由采样得到的历史栅距的通过时间构成的时间序列比较平滑，光栅通过当前栅距的时间Δt与上一个栅距的通过时间具有强的相关性。指数平滑法通过给过去的样本观测值不一样的权重，使距离当前预测样本时间越近，获得的权值越大[17]。因此,可通过构建应用指数平滑法的光栅信号细分模型来对时间进行预测，实现光栅细分。

2.1 一次指数平滑法

采样时间样本Δti,Δti+1，…，Δti+n-1,为光栅通过前n个栅距时的时间，根据一次指数平滑法有：

(1)

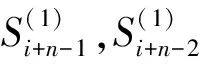
(2)

即对第i+n个栅距的预测时间为ΔTi+n,有

ΔTi+n=αΔti+n-1+(1-α)ΔTi+n-2

(3)

进一步展开有

(4)

记β=1-α(0<α<1)，式(4)可化简为

(5)

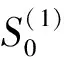
2.2 二次指数平滑法

一次指数平滑预测算法具有简单、运算快的优势，但当样本序列的变动具有近似直线的趋势时，如光栅传感器做匀加速运动时，使用一次指数平滑法进行预测将会带来滞后偏差。因此，通常在一次平滑的基础上再一次进行平滑处理，能够实现更精确的预测。

(6)

则根据二次指数平滑法得到预测结果为式(7)。

(7)

(8)

式中k为时间跨度，表示预测的长远程度，预测越长远即k值越大，那么带来的误差也就越大。由于光栅传感器运动过程中具有连续性，观测样本数据可实时更新，因此本系统所做预测均为近期预测，所以令k=1。最终预测结果如式(9)所示。

(9)

2.3 初始值的确定

(10)

2.4 平滑系数α的确定

利用指数平滑法进行建模预测时，平滑系数反映了数学模型对历史数据变化的灵敏程度，因此对平滑系数α的确定是关键，α的选择是否合适对最终的预测效果有较大影响。传统的确定平滑系数的方法有经验估计法、试凑法、0.618选优法等。利用经验估计法获取平滑系数简单迅速，但是最终预测误差较大；而0.618选优法能够确定最优的α值，使得最终的预测效果较好,但算法复杂[20-22]。在本系统中利用预测算法进行光栅软细分不仅要考虑预测效果，而且不可忽略光栅细分过程中的实时性。因此，本系统考虑使用经验估计法和0.618选优法结合的组合算法来确定最终的平滑系数。针对光栅传感器不同的运动阶段得到的观测样本序列稳定性不同的特点，先利用经验估计法缩小平滑系数的取值范围，然后利用0.618选优法搜寻最优平滑系数。

2.4.1 平滑系数经验估计法

光栅在不同的运动状态时，由于外界的干扰或自身运动状态的特点，得到的观测样本序列稳定性不同，而经验估计法则是根据观测样本序列的稳定性来确定最终的平滑系数。经验估计法选优标准如下：

1) 当样本序列趋于稳定、数据变化不大时平滑系数应取得小一些，一般α取值域为(0.1，0.4)。此时模型中的各期权数没有较大差别，使得修正幅度比较小，最终的预测结果中有比较多的历史观测样本序列成分。此时对应光栅传感器运动过程中的相对高速近似匀速运动过程(此时光栅运动稳定)。

2) 当样本序列波动较大时，平滑系数取值域为(0.4，0.6)，对应于光栅运动过程中的加速过程中的稳定阶段和相对低速近似匀速运动过程(此时光栅运动不太稳定)。

3) 当样本序列波动很大时，平滑系数应取大一些，通常取值域为(0.6，0.8)。较大的平滑系数能够使得整个数学模型对历史变化有大的灵敏度，使得最终预测值能与观测样本数据变化同步。此时，对应于光栅运动过程中数据变化非常大的过程，如光栅由匀速运动到变速运动的过渡阶段(光栅运动很不稳定)。

考虑按照以上标准使用经验估计法来初步确定光栅在不同运动阶段时平滑系数取值范围，提高细分过程中的实时性。

2.4.2 平滑系数0.618选优法

利用0.618选优法确定平滑系数，首先要确定目标函数，在本系统中考虑使用平均绝对百分比误差MAPE作为目标函数，如式(11)所示。

(11)

将平滑系数取值域(0.1,0.4)划分为3个子域(0.1,0.2)、(0.2,0.3)、(0.3,0.4)依次对每个子域(Xi，Yi)执行以下步骤：

① 计算αi=0.618Xi+0.382Yi。

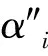
选优部分流程如图2所示。

3 预测细分硬件系统设计

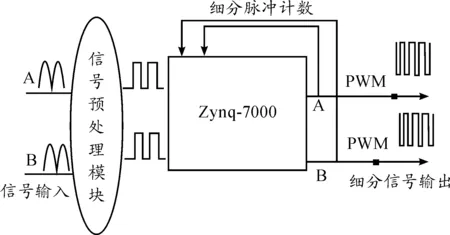
图3 光栅预测细分硬件系统框图

图3为本系统的硬件系统框图。常见的光栅传感器输出信号为两路相位相差90°的正弦波。图3中的信号预处理模块主要由过零检测器构成，其功能是将两路正弦波转化为两路PWM波。图中Zynq-7000为一款集成了FPGA和ARM内核的嵌入式芯片。将FPGA和ARM组合运用在本系统中主要实现以下功能：

① 对PWM波进行计数并辨向。

② 获取观测样本数据并建立基于二次指数平滑法的数学模型，对下一个栅距的运行时间进行预测。

③ 对误差进行实时修正。由于实验过程中总存在误差，为消除误差累计，需要对细分前和细分后的脉冲进行计数，然后根据细分前后脉冲计数的差值修正下一次的细分脉冲输出量。

④ 依据细分倍数和细分误差，输出对应的细分脉冲。

4 细分实验研究

图4 光栅细分实验系统

图4为本系统的实验平台，为保证实验结果的可靠性，需要作对比实验进行验证。图4中光栅1和光栅2为两个分辨率相同的光栅传感器(均来自HEIDENHAIN公司)，但利用到的细分方式不同，光栅2采用的是基于二次指数平滑算法的软细分方式，而光栅1利用HEIDENHAIN公司的IBV660B细分盒进行细分。为保证光栅1和光栅2运动状态一致，将它们与数控转台同轴安装。由于实验过程中光栅传感器微小的速度变化都能影响实验结果，因此实验平台考虑利用PMAC可编程的多轴控制器对速度进行精确的控制，方便对不同运动状态下的光栅细分效果进行研究。

图5为光栅传感器在PMAC控制器控制下的光栅运动时间-位移图。起始位移为45.07°,终止位移为82.81°,运行总时间为10.937 4 s。图6为对应过程中的速度变化曲线，为了检验光栅传感器在不同的运动状态下的细分效果，令光栅分别运动在低速匀速状态、匀加速状态、高速匀速状态以及匀减速状态，最后回到低速匀速状态，分别对应于图6所示的阶段1～5。

图5 光栅运动时间-位移曲线

图7为根据本算法得到的预测采样时间误差，对数据和图形进行分析可得：

1) 在光栅作相对低速运动的过程中，如图7中所示1和5阶段，由于此时PMAC控制系统的振动对光栅传感器干扰较大，导致系统不稳定，故此时的预测误差较大，预测效果能控制在±0.078 ms以内。

2) 在光栅作匀加速和匀减速运动时，如图7中2和4阶段，这两个阶段的中间过程由于光栅运动趋势相对稳定，因此数据波动不大，而在2和4阶段的开始过程和结束过程中，光栅传感器处于由匀速运动到加速运动或加速运动到匀速运动的“临界”阶段，故此时数据波动很大。因此，在整个运动过程中预测误差也最大，预测效果只能控制在±0.12 ms以内。

3) 图7中阶段3的预测误差最小。因为此时光栅传感器运动在相对高速阶段，PMAC控制系统带来的影响较小。此时系统稳定，数据波动较小，预测效果能控制在±0.048 ms以内。

图8为系统细分误差图，对数据和图形进行分析可知：

1) 细分效果最好的阶段出现在光栅传感器作相对高速近似匀速运动时，即图8中3阶段，细分误差能控制在±0.67″。

2) 当PMAC控制系统带来的干扰较大时,如图8中1和5阶段，细分误差只能控制在±0.89″。

3) 细分效果最差出现在光栅运动趋势不稳定、数据波动较大时，如图8中2和4阶段中的匀速运动与加速运动过渡过程中的“临界”阶段，细分误差为±1.35″。

图7 预测采样时间误差

5 结束语

本文提出一种基于指数平滑法的光栅信号细分新方法，与传统的细分方法不同，此方法不依赖于光栅传感器输出信号的质量，充分利用现有的工艺制造水平，将对空间的测量转换为对时间的预测。

结合光栅传感器的运动特点,通过对采样的时间序列进行应用二次指数平滑法的数学模型的建立。在预测过程中给不同的采样观测值不同的权重，从而实现对下一个栅距运行时间准确的预测。由于二次指数平滑法的预测效果受平滑系数的影响较大，考虑到兼顾光栅传感器细分过程中的细分实时性和细分准确性，本文充分利用平滑系数经验估计法以及0.618选优法两种算法的优势，构成组合式的平滑系数优选算法，从而确定最优的平滑系数，以实现又快又准的预测细分。

整个系统的预测效果和细分效果与样本时间序列的稳定性相关，当外界干扰较大或者光栅传感运动趋势不稳定时，预测和细分效果较差。而当数据波动小，系统稳定时，预测效果较好。最终对实验数据的研究分析结果表明：实验结果达到要求，将指数平滑法运用到预测细分模型中能对光栅进行精密细分。

[1] 陈自然，刘小康，郑永，等.精密位移动态测量信号特征辨识及细分新方法研究[J].仪器仪表学报，2015，36(10):2224-2230.

[2] WANG M S，KUNG Y S，TU Y M，et al.Novel interpolation method for quadrature encoder square signals[C]//IEEE International Symposium on Industrial Electronics.[S.l.]:IEEE，2009:333-338.

[3] 冯济琴，刘浩，陈自然，等.基于域变换和灰色预测的光栅信号软细分方法[J].仪器仪表学报，2016，37(2):263-270.

[4] 彭东林，练俊君，陈锡候，等.基于时间序列的时栅转台误差修正研究[J].重庆理工大学学报(自然科学)，2015(1):96-100.

[5] 黄元申，董成成，黄运柏，等.光栅刻划机直线度误差补偿的研究[J].光谱学与光谱分析，2017，37(3):946-951.

[6] 刘柯，宋金城，陈秀政.基于TMS320F2812的光栅细分卡的设计[J].红外与激光工程，2008，37(Z):242-245.

[7] 钱伟，康鲁湛.基于DSP的光栅分度盘及其光栅信号精细分[J].测控技术，2012，31(10):34-36.

[8] 刘清.用DSP实现光栅高准确度细分技术[J].传感器技术，2003，22(7):25-27.

[9] 丁旭，李彬华，杨晓晗.一种基于FPGA的光栅信号细分方法[J].传感技术学报，2016，29(6):847-852.

[10] 汪涛，杜立剑.基于Niosll的光栅细分电路系统设计[J].单片机与嵌入式系统应用，2010(5):32-35.

[11] 郭雨梅，苏升.基于智能数字锁相技术的光栅细分方法[J].仪表技术与传感器，2015(1):104-107.

[12] FLEMING A J.A review of nanometer resolution position sensors:Operation and performance[J].Sensors & Actuators A Physical，2013，190(1):106-126.

[13] 赵勇，苏显渝，张启灿.绝对编码光栅的相位细分及其在位移测量中的应用[J].光学学报，2011，31(8):135-139.

[14] EMURA T，WANG L.A High-Resolution Interpolator for Incremental Encoders Based on the Quadrature PLL Method[J]． Industrial Electronics，IEEE Transactions on，2000，47(1):84-90．

[15] 陈自然，彭东林，刘小康，等.基于支持向量机时栅数控转台时序预测研究[J].仪器仪表学报，2012，33(8):1793-1799.

[16] CHEN Z R，LIU X K，PENG D L，et al.Dynamic Model of NC Rotary Table in Angle Measurements with Time Series[J].Transactions of the Institute of Measurement and Control，2013，35(2):181-187.

[17] 廖耀华.基于改进指数平滑法和马尔科夫模型的风速预测研究[J].电力科学与技术学报，2016(3):86-89.

[18] 张林军，邢晓明.平滑系数的最优估计方法研究[J].西安工业学院学报，1998，18(3):217.

[19] 何舒华，何霭琳.指数平滑法初始值计算与平滑系数选取的新方法[J].广州大学学报(自然科学版)，2011(22):6-10.

[20] 钱任庚.一种用0.618优选法优化平滑系数的方法[J].系统工程，1994，12(2):59-61.

[21] 余有芳.指数平滑系数的优化研究[J].科技通报，2010，22(6):817-820.

[22] 王勇领.预测计算方法[M].北京:科学出版社，1986.