准零刚度隔振器的时域仿真

牛宝良

(中国工程物理研究院 总体工程研究所， 四川 绵阳 621999)

普通隔振器总存在一个共振频率，在共振频率及其附近起不到隔振作用，反而有放大作用，这个问题一直困扰着振动工程界。1980年初Alabuzhev等[1]基于正负刚度并联原理开发了一些准零刚度(QZC)隔振器，并简单验证了机构的隔振特性。与未使用负刚度的机构相比，准零刚度隔振机构具有显著的低频隔振效果。之后，国内有学者一直在研究准零刚度隔振器。湖南大学彭献等[2-6]从20世纪80年代后期开始了相关研究；徐道临团队[7-14]近年来做了大量的研究，提出了几种线振动的QZS隔振器构型及相应的分析方法，并进行了试验研究，也提出了扭振动的QZS构型和分析；南京航空航天大学王勇等[15]在QZS隔振器的应用方面进行了探索，包括车-座椅-人耦合模型的响应分析[15]、含有QZS的有源无源混合隔振控制[16]。海军工程大学柴凯等[17]提出了基于磁性负刚度的QZS隔振器及其设计方法。国外也有相关的研究报道，Kyoung-Rock Kim[18]研究了宽负载范围的QZS设计；Pham Van Trung[19]研究了有源无源QZS隔振器，消除了无源QZS遇到的放大现象；Ali Abolfathi[20]研究了QZS参数失调情况下的隔振效果。总之，作为一种低频隔振性能优越的隔振器，准零刚度隔振器在构型设计、性能分析等方面正处于持续研究中，相关的研究成果多是基于频域的。准零刚度隔振器含有显著的非线性特性，时域仿真能准确地描述其非线性特性，其仿真结果也更加直观明了。因此，本文对准零刚度隔振器进行建模和时域仿真。

1 准零刚度隔振器

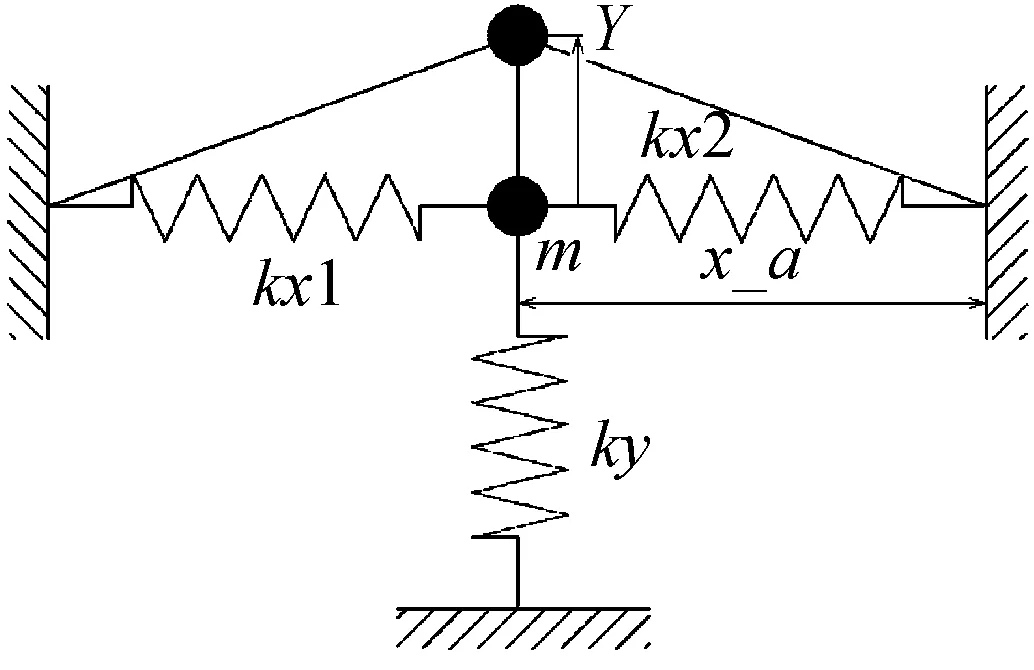
图1 QZS隔振器结构示意图

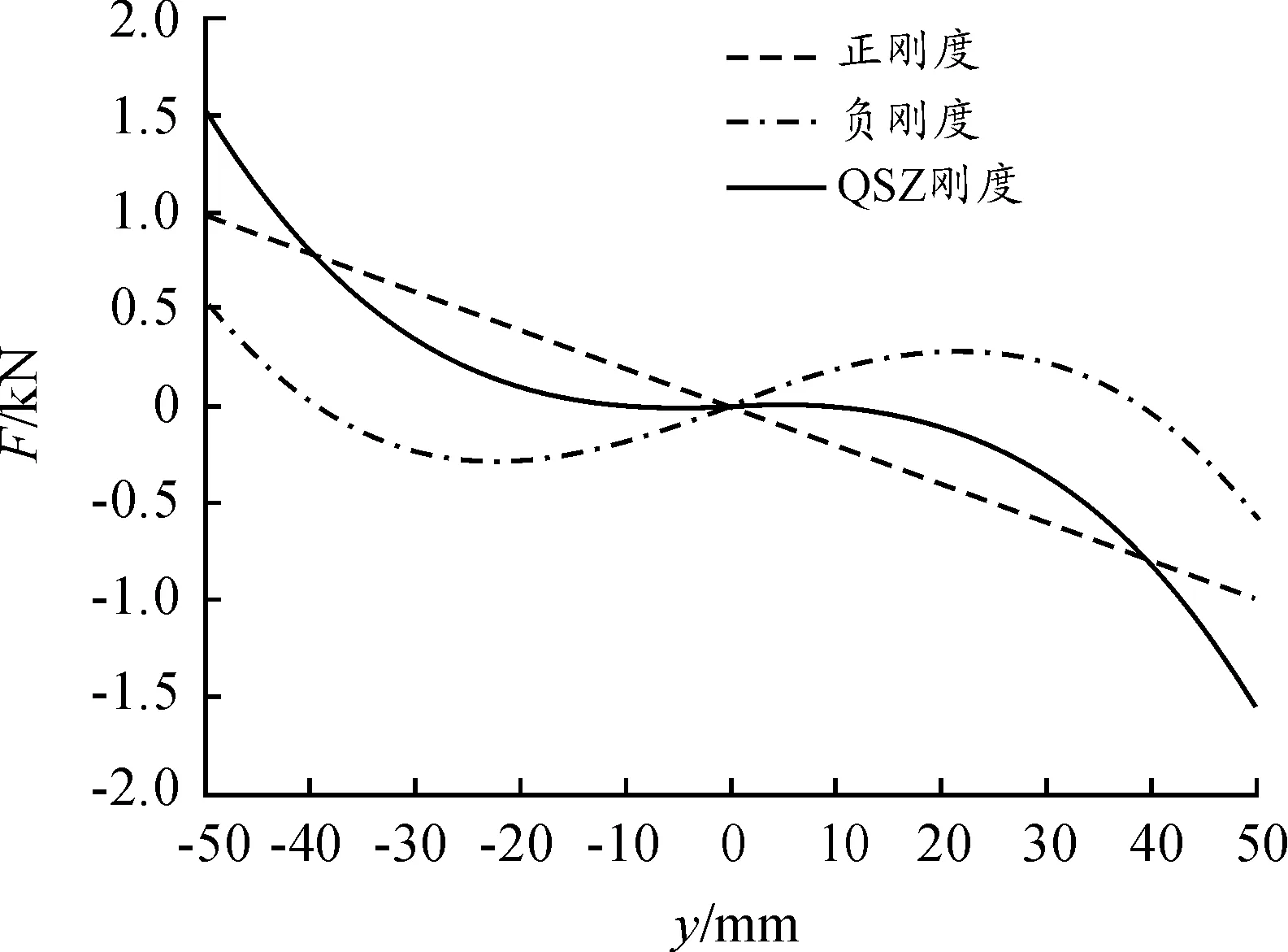
图2 正刚度、负刚度、QZS刚度力-位移曲线

准零刚度隔振器一般的构成办法是正刚度弹簧、负刚度弹簧并联，合理搭配正负刚度参数，使得在零位附近一个区间刚度为0或者接近0。最典型的代表是Carrella等[7]将3个线性或者非线性弹簧进行组合，通过参数优化得到的一种QZS系统。本文所要仿真的也是这种准零刚度隔振器。一个垂直向的弹簧支承负载质量，是正弹簧刚度，两个水平向对顶的弹簧构成竖直向的负刚度弹簧(在零位附近的一个区间)。QZC隔振器结构示意图如图1所示。

QZS隔振器的垂直弹簧设计与普通隔振器相同，根据已知负载质量、隔振器的弹簧刚度，允许的最大变形量确定垂直弹簧的参数，然后设计水平弹簧的尺寸、刚度、预压缩量，使得在一定范围内综合弹簧刚度基本为0。不失一般性，给定一组参数，质量m=10 kg，竖向弹簧刚度ky=19 613 N/m，阻尼系数为44.287 N/(m/s)(阻尼比为0.05)，横向弹簧刚度kx1=kx2=15ky。它的正刚度、负刚度、组合后的零刚度曲线见图2。在Y向±10 mm范围内，达到准零刚度。

2 准零刚度隔振器建模

为通过仿真了解QZS隔振器的隔振性能，建立了基于Matlab/Simulink的仿真模型。

2.1 隔力模型

这类隔振系统希望传递到基础的力更小，建立的仿真模型如图3所示，其中QZS弹簧仿真模型如图4所示。

2.2 隔幅模型

这类隔振系统希望基础振动传递到质量m上的运动更小，激励是基础的运动。建立的仿真模型如图5所示，其中QZS弹簧仿真模型如图6所示。

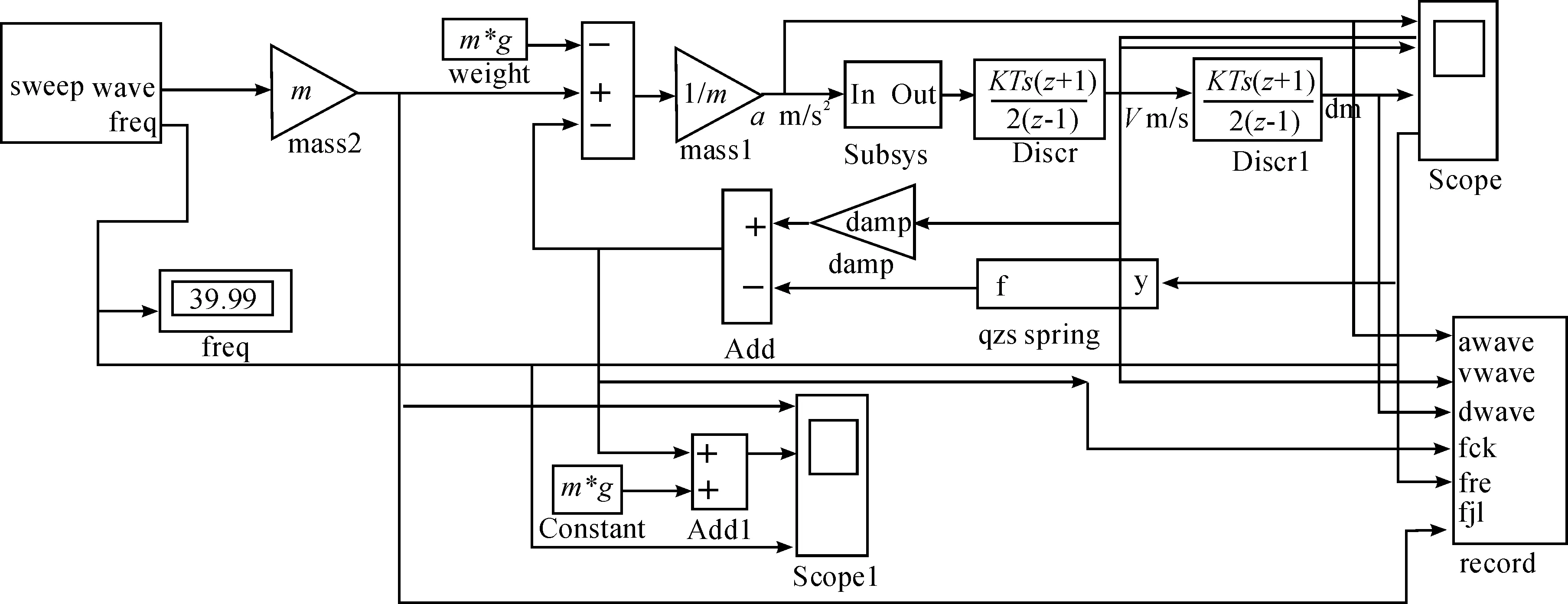
图3 QZS隔振器(隔力)仿真模型

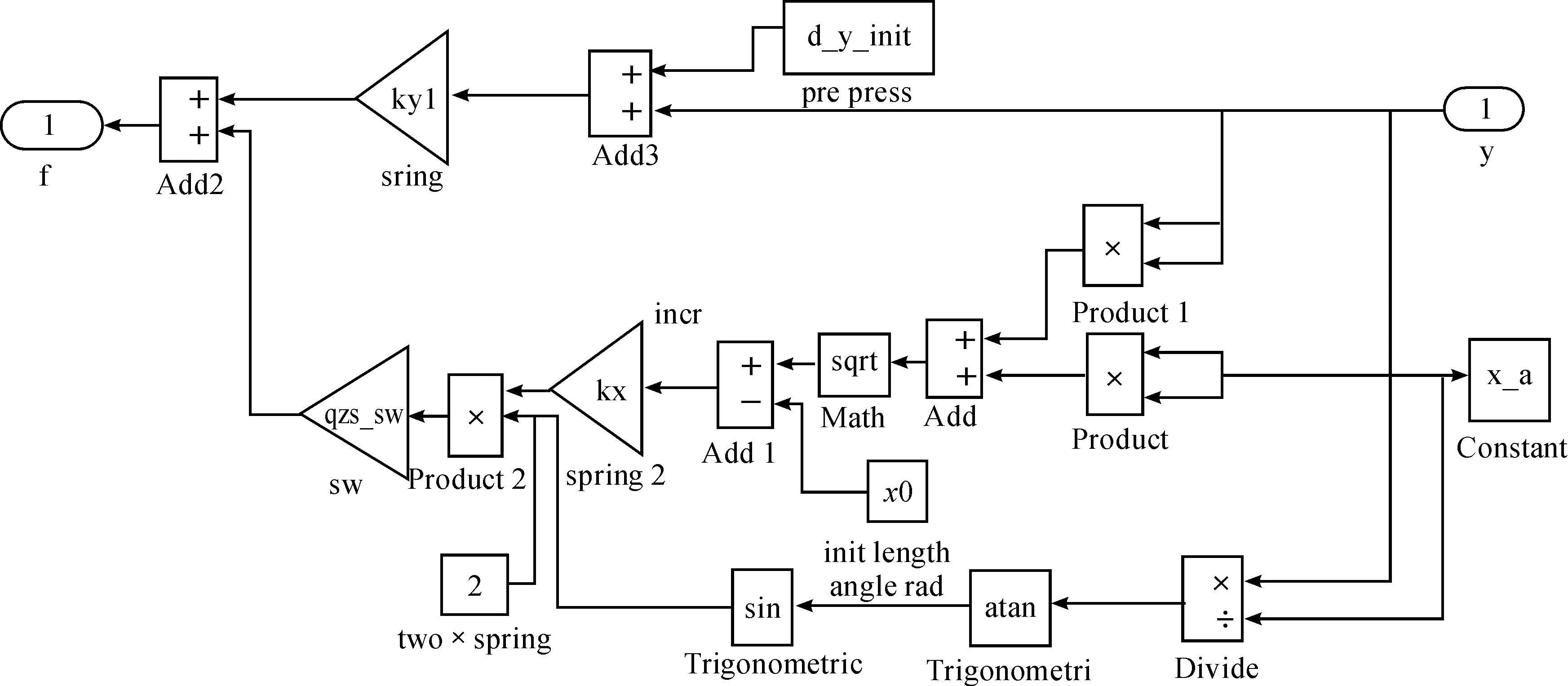
图4 QZS弹簧仿真模型

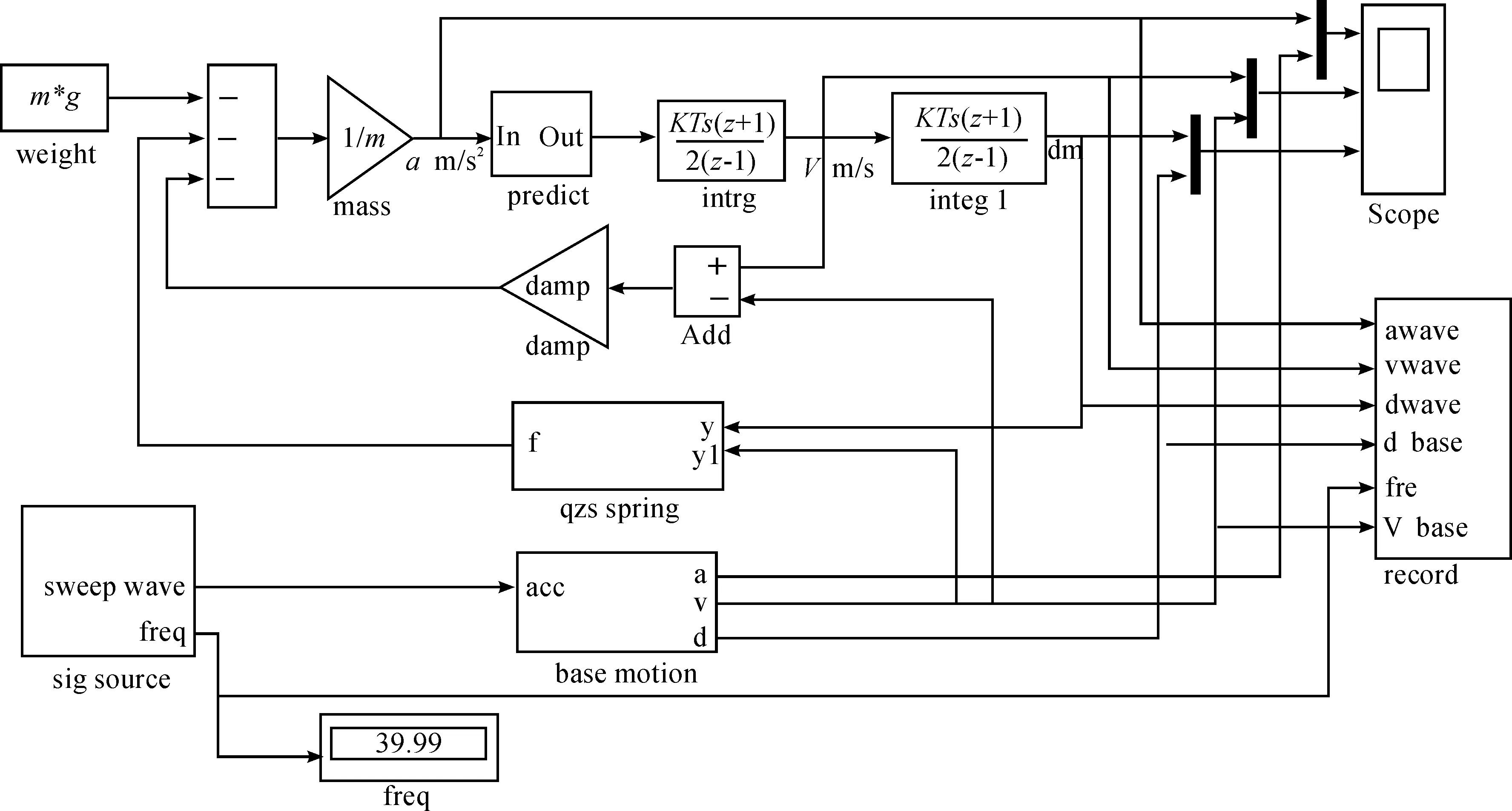
图5 QZS隔振器(隔幅)仿真模型

2.3 冲击隔离模型

这类隔振系统希望基础冲击传递到质量m上的运动更小。激励是基础的冲击运动，建立的仿真模型与图5类似，区别在于激励波形。这里给出的激励是一个由半正弦3次方构造的一个冲击位移波形，它具有速度零起始零结束、加速度零起始零结束的特性，可以模拟路面凸起。它的加速度、位移、速度波形如图7所示。仿真模型与图5、6基本一致，区别只是基础位移的生成。它的参数只有2个：位移幅值、脉冲宽度。

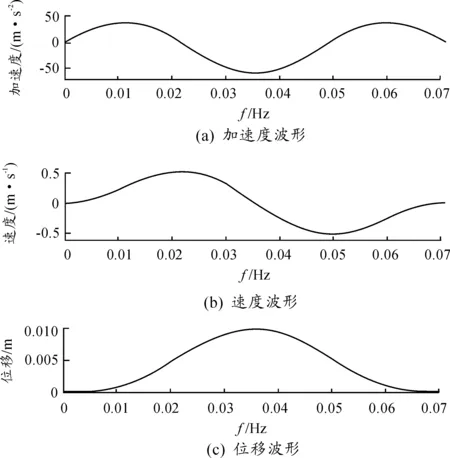
图7 冲击激励波形

3 仿真分析

3.1 隔力仿真

低于这个临界状态，比如位移为3 mm时，则呈现非常好的衰减，力比最大值为0.65，而且随着频率增加呈现单调下降的趋势，如图9所示。

高于这个临界状态，比如预期位移为5 mm时，它低频段呈现严重的恶化，2.6 Hz以下呈现放大状态，最大放大5倍，大于2.6 Hz以后，进入良好衰减状态，如图10所示。

局部的时域波形如图11所示。在放大阶段，位移达到±15 mm时，加速度呈现非常明显的非正弦特征。究其原因，就是位移太大，进入了弹簧的非零区，而且这个非零区由于负刚度弹簧的非线性使得综合刚度呈现非线性，因此响应加速度呈现非线性，从而导致波形失真。

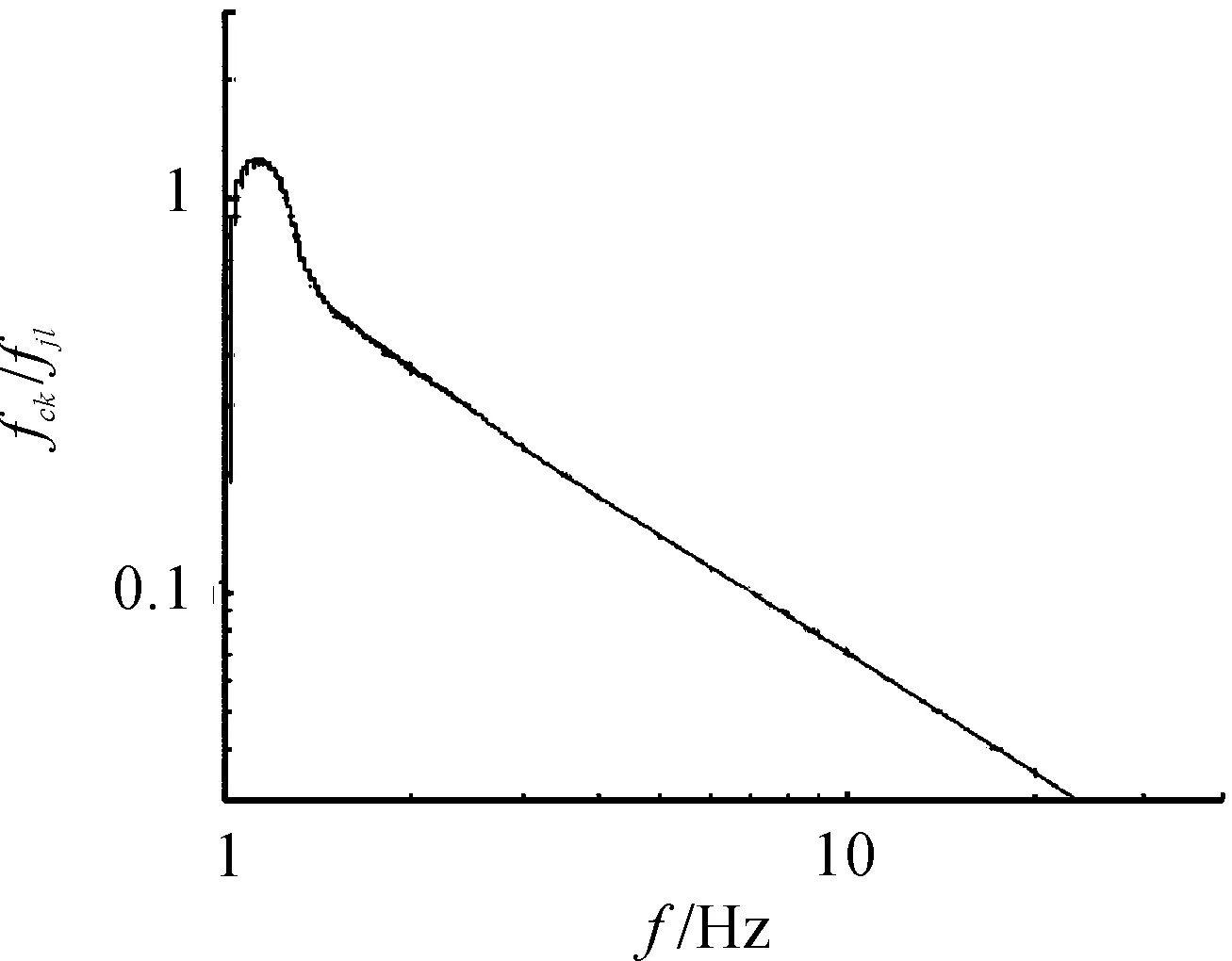
图8 位移达到±4 mm时的力比曲线

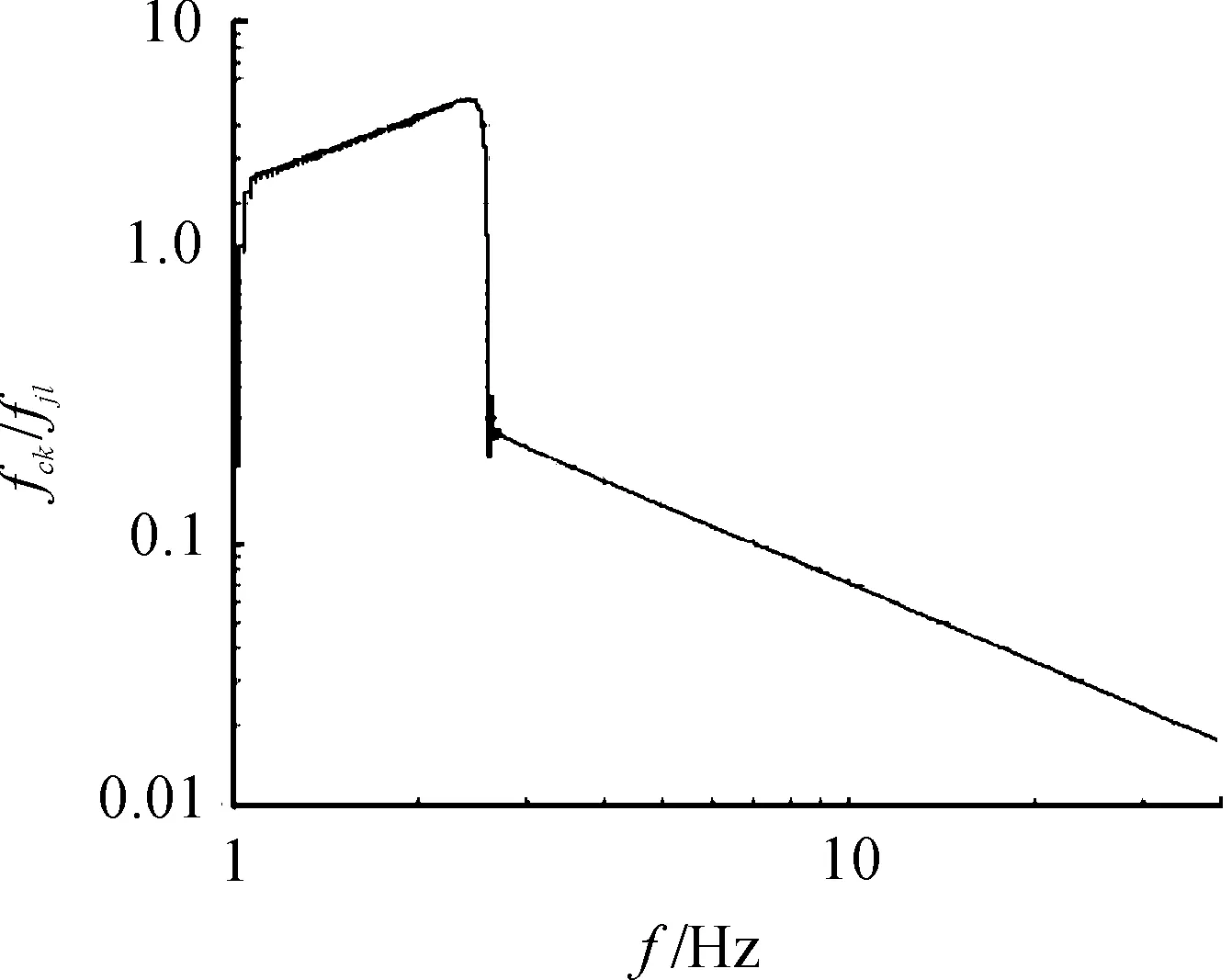
图10 位移达到±15 mm时的力比曲线

3.2 隔幅仿真

隔幅，就是希望基础激励时质量m的运动幅值小。这里用m的振动位移/基础的激励位移(以下简称位移比)来衡量。

通过仿真发现：对于所给定的这组参数，当振动位移达到4 mm时，传递到基础的力与激励力之比略超1，如图12所示。这是一个临界状态。

低于这个临界状态，比如位移为3 mm时，则呈现非常好的衰减，力比最大值为0.65，而且随着频率增加呈单调下降的趋势，如图13所示。

高于这个临界状态，比如基础振动位移为5 mm时，其低频段呈现严重的恶化。质量m的振动位移达到17.526 mm，位移比曲线如图14所示，2.6 Hz以下呈现放大状态，最大放大3.8倍。从放大转衰减的过渡过程的时域曲线见图15。加速度也严重失真，但是与隔力时的加速度波形失真有所不同。

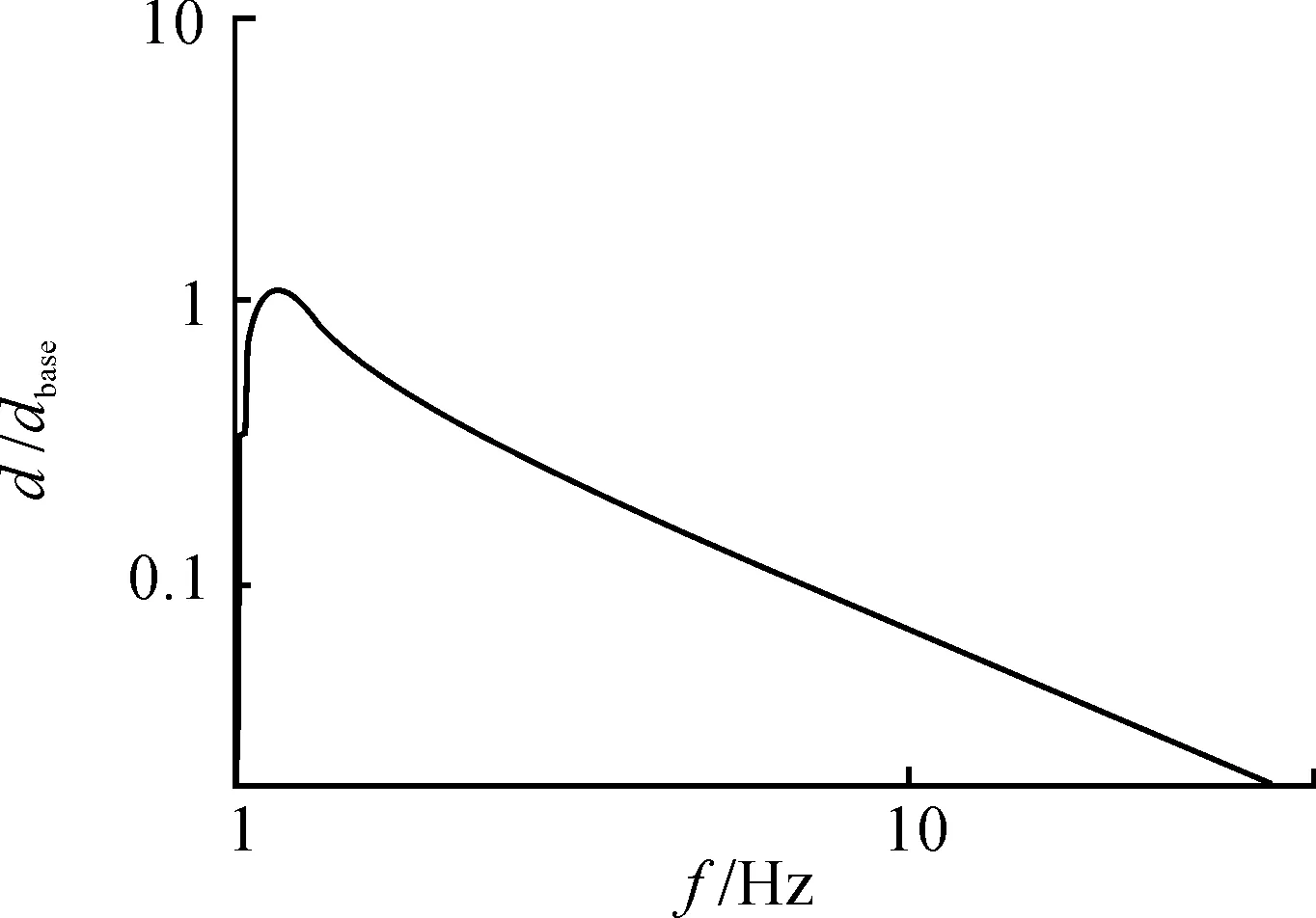
图12 基础位移达到±4 mm时的位移比曲线

图14 基础位移达到±5 mm时的位移比曲线

3.3 隔冲击仿真

隔冲击，就是希望在基础激励时质量m的运动幅值小。这里用m的振动位移/基础的激励位移(以下简称位移比)来衡量。同时也给出速度比、加速度比，以方便比较。

后来我一直没去景花厂。阿花邀请过我，我就说忙。忙不过是个借口，实际上是我不想去。我是个老实人，不喜欢趋炎附势那一套。虽然我对美女从不敬而远之，但当美女和老板合二为一时，我会牢牢抓住心猿意马的缰绳，敬而远之了。还有，大家都是做抛光的，总往哪儿跑怕别人会有想法，所以，不去为好。

如前所述，基础冲击激励采用冲击位移，它的参数是幅值、脉宽。以隔振器的共振周期作为参考。

当激励位移取10 mm、激励脉宽取隔振器共振周期(不考虑负刚度时的普通隔振器)时，普通隔振器质量m的振动响应如图16所示。

QZS隔振器的响应如图17所示。响应加速度峰值比为0.089 839，速度峰值比为0.226 85，位移峰值比为0.428 6。由图17可见呈现良好的隔振效果。

当激励脉宽取隔振器共振周期的2倍时，响应加速度峰值比为0.197 21，速度峰值比为0.454 96，位移峰值比为0.656 44。

当激励脉宽取隔振器共振周期的4倍时，响应加速度峰值比为0.633 11，速度峰值比为0.774 13，位移峰值比为0.917 08。

当激励脉宽取隔振器共振周期的8倍时，响应加速度峰值比为1.159 8，速度峰值比为1.279 5，位移峰值比为1.050 8。

当激励脉宽取隔振器共振周期的40倍时，响应加速度峰值比为0.977 83，速度峰值比为1.089 9，位移峰值比为1.026 1。

当激励脉宽取隔振器共振周期的0.5倍时，响应加速度峰值比为0.041 171，速度峰值比为0.103 88，位移峰值比为0.298 74。

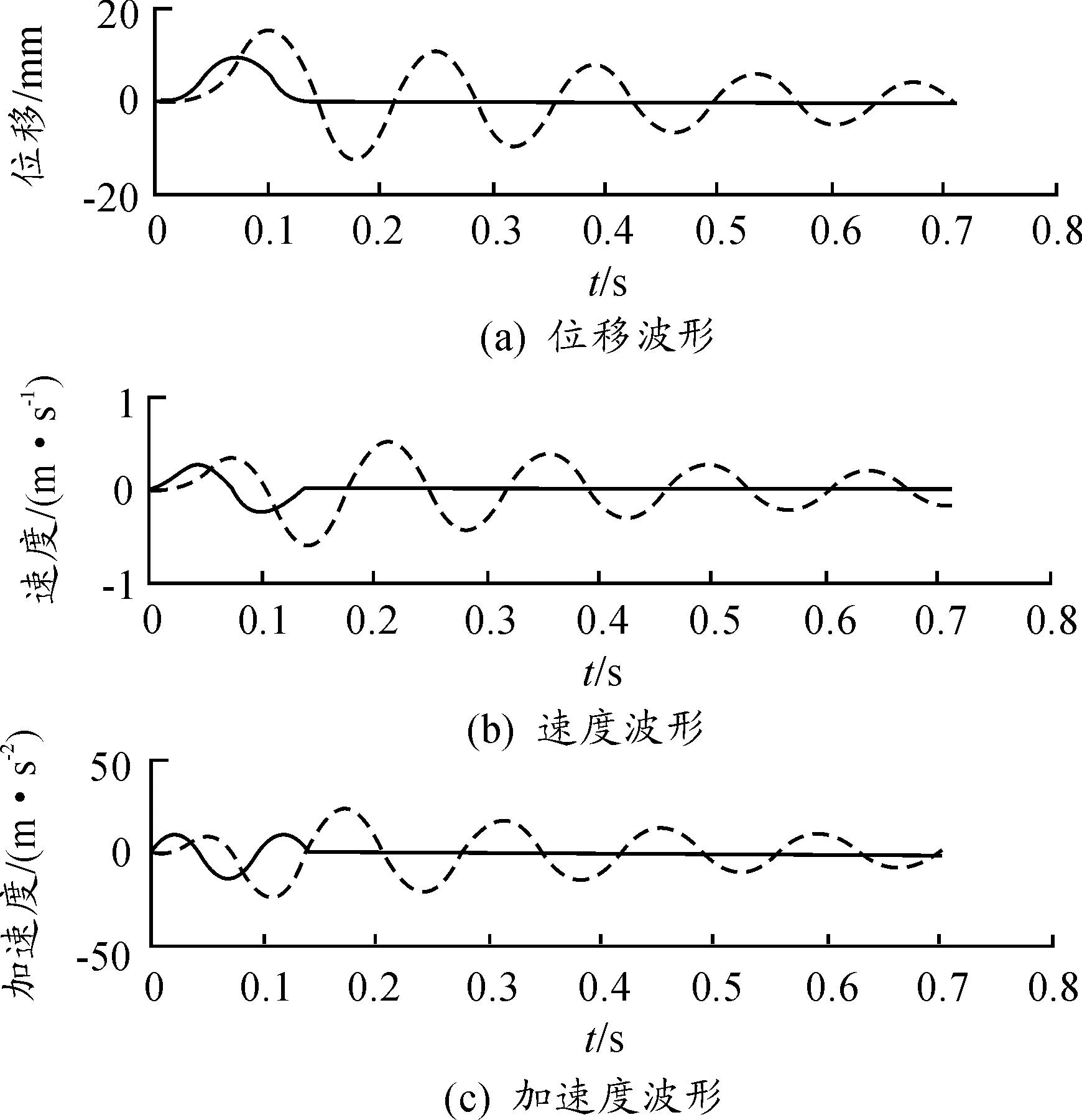
图16 普通隔振器的冲击响应

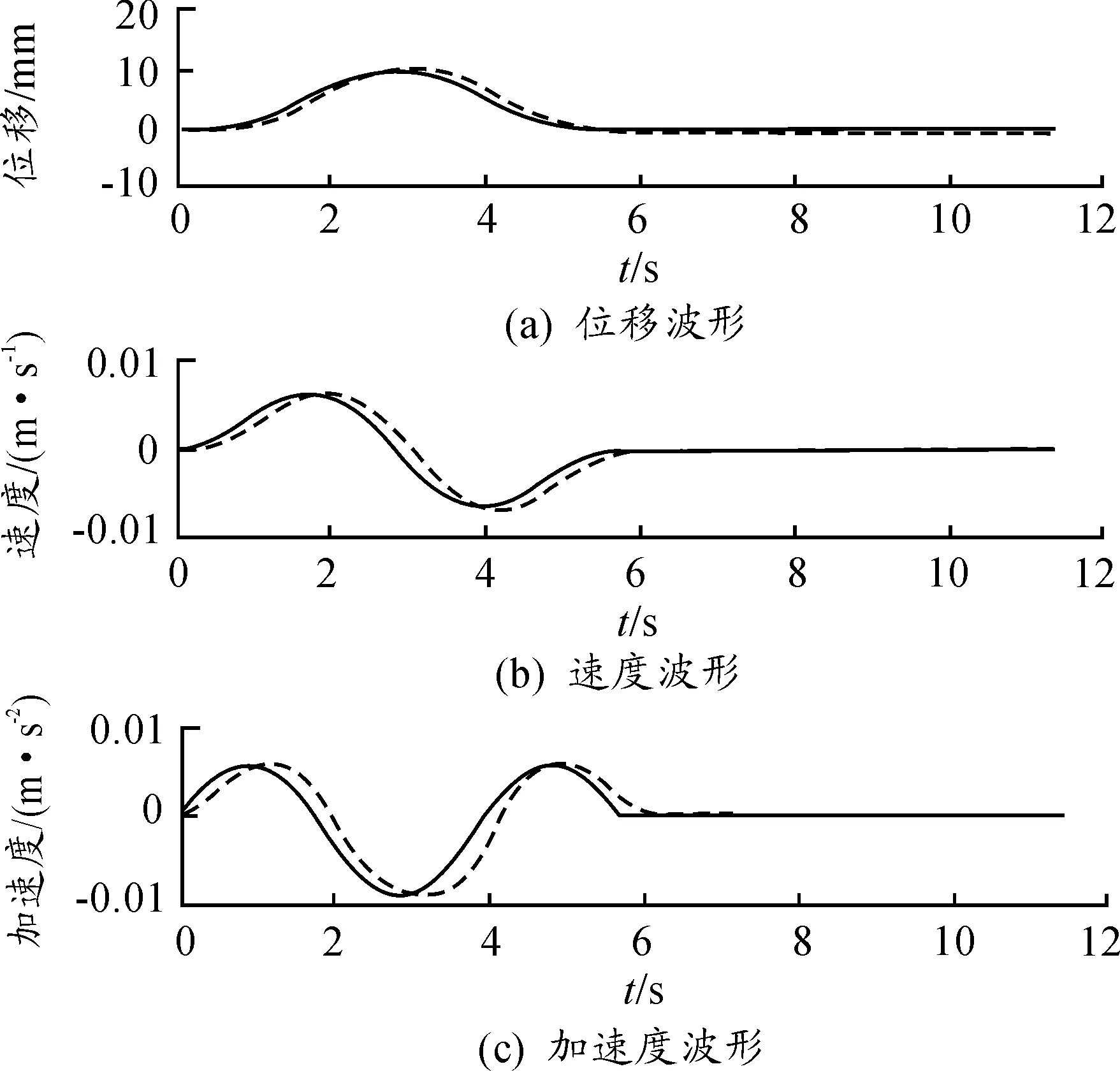
图18 QZS隔振器的冲击响应(40×1/fn)

从以上数据可以得出：基础振动为10 mm时，在脉宽4倍共振周期以下，位移、速度、加速度都是衰减的，脉宽越小，衰减越好；在脉宽4倍共振周期以上至8倍共振周期，基本在幅值比为1附近，有轻微放大；在8倍以上，位移比、速度比、加速度比都基本上为1，因为这时频率很低，质量m基本上与基础同步运动。

4 结束语

本文建立了基于正负弹簧刚度合成的QZS隔振器的时域仿真模型，开展了隔力、隔幅、隔冲击仿真。

仿真模型运行正确快速，为QZS隔振器的参数设计提供了方便。

尽管只对一组QZS隔振器数据进行了仿真，但仿真结果揭示了客观规律，即：在激励幅值比较小的情况下，QZS隔振器无论是隔力、隔幅都非常好，全频段不会出现共振放大现象；激励幅值超过临界值以后，则会在低频段出现放大现象，这提示设计者在应用QZS隔振器时需要对激励的幅值、频率范围加以分析预判。

对于冲击基础激励，QZS隔振器性能非常好，在激励位移达到10 mm(对于本文QZS隔振器，10 mm对应零刚度区域)的情况下，在小脉宽(小于4倍共振周期)时，衰减效果很好，脉宽越小衰减越显著。40倍共振周期以上，基本不衰减不放大。总之，对于冲击来说，QZS隔振器是适合的。

本文仅作了参数设计与仿真，具体的效果还与QZS隔振器的工程实现结构相关，还需进一步研究。

[1] 憂高法.新巧准零刚麼隔振平台减振机理及动力学性态研究[D].芜湖:安徽工程大学，2016.

[2] 陈树年，黄天择，彭献.汽车座椅弹性元件刚度的探讨[J].湖南大学学报(自然科学版)，1989，16(3):14-20.

[3] 彭献，陈树年，宋福磐.负刚度的工作原理及应用初探[J].湖南大学学报(自然科学版)，1992，19(4):89-94.

[4] 彭献，黎大志，陈树年.准零刚度隔振器及其弹性特性设计[J].振动、测试与诊断，1997，17(4):44-46.

[5] 彭献，张施详.一种准零刚度被动隔振系统的非线性共振响应分析[J].湖南大学学报(自然科学版):2011，38(8):34-39.

[6] 彭献，张施详.一种准零刚度被动隔振系统的静力与线性动力特性分析[J].力学季刊，2012，33(3):492- 498.

[7] 徐道临，张月英，周加喜，等.一种准零刚度隔振器的特性分析与实验研究[J].振动与冲击，2014，33(11):208-213.

[8] XU D，ZHANG Y，ZHOU J，et al.On the analytical and experimental assessment of the performance of a quasi-zero-stiffness isolator[J].Journal of Vibration and Control，2014，20(15):2314-2325.

[9] ZHOU J，XU D，BISHOP S.A torsion quasi-zero stiffness vibration isolator[J].Journal of Sound and Vibration，2015，338:121-133.

[10] ZHOU J，WANG X，XU D，et al.Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam-roller-spring mechanisms[J].Journal of Sound and Vibration，2015，346:53-69.

[11] 王心龙.CRSM准零刚度隔振器的非线性隔振特性及实验研究[D].长沙:湖南大学，2015.

[12] 周杰.碟形橡胶准零隔振器的设计与特性分析[D].长沙:湖南大学，2015.

[13] 周加喜，徐道临.单层准零刚度浮筏隔振特性分析及混沌化[J].中国科技论文，2014，8(8):911-915.

[14] 徐道临，周杰，周加喜，等.碟形橡胶准零刚度隔振器的设计和特性分析[J].湖南大学学报(自然科学版)， 2015，42(8):22-28.

[15] 王勇，李舜酩，程春.基于准零刚度隔振器的车-座椅-人耦合模型动态特性研究[J].振动与冲击，2016，35(15):190-196.

[16] 王勇，李舜酩，程春，等.立方速度反馈控制的准零刚度隔振器动力学特性分析[J].振动工程学报，2016，29(2):305-312.

[17] 柴凯，杨庆超，朱石坚，等.矩形永磁铁的磁力计算及其应用[J].噪声与振动控制，2016，36(6):51-55.

[18] KIM K R，YOU Y H，AHN H J.Optimal design of a QZS isolator using flexures for a wide range of payload[J].Int J Precis Eng Manuf，2013，14(6):911-917.

[19] VAN T P，KIM K R，AHN H J.A nonlinear control of an QZS isolator with flexures based on a lyapunov function[J].International Journal of Precision Engineering and Manufacturing，2013，14(6):919-924.

[20] ABOLFATHI A，BRENNAN M J，WATERS T P，et al.On the effects of mistuning a force-excited system containing a quasi-zero-stiffness vibration isolator[J].Journal of Vibration and Acoustics，2015，137(4):044502-0044507.