基于核函数的联合稀疏表示高光谱图像分类
2018-03-14陈善学周艳发漆若兰
陈善学, 周艳发, 漆若兰
(重庆邮电大学移动通信技术重庆市重点实验室, 重庆 400065)
0 引 言
高光谱图像具有较高的空间与光谱分辨率的这一特点使其被广泛的应用于各个领域,例如在军事、环境、海洋、地理、农业等领域。在以上的这些领域里,高光谱图像的分类已经成为一个非常重要的研究内容之一。在高光谱图像中,每个像元(或像素)都是一个高维的光谱曲线向量。在一定光谱波段,不同的地物具有不同的反应(吸收或反射)。因此,人们可以根据它们的光谱曲线对地物进行识别和分类。
基于高光谱图像的光谱特征,各种分类方法被提出,例如支持向量机(support vector machine, SVM)方法和其他基于核的分类方法[1-4],人工神经网络(artificial neural network, ANN)[5]。最近,基于稀疏表示(sparse representation, SR)的分类方法[6-8]越来越多地被应用于高光谱图像的分类,稀疏表示分类(sparse representation classification, SRC)方法通过全部训练样本的稀疏线性组合来重构表示一个测试样本,然后通过最小表示残差来分类测试样本。通过一种协同表示机制,在高光谱图像的分类中,SRC表现出了比较良好的分类性能。文献[9]提出一种基于稀疏表示的任务驱动字典学习算法,该算法仅仅用了少量的训练样本。文献[10]通过利用相邻像元之间具有相似的特性,将其最近的相邻像素对所有像素进行空间平均,形成一种联合协作表示形式,极大地提高了算法的分类精度。通过加入空间信息,文献[11]提出一种联合稀疏表示模型(joint sparse representation model, JSM),或者同时正交匹配追踪(simultaneous orthogonal matching pursuit, SOMP),在该模型中待测试像元与其空间邻域的像元通过少量共同的训练样本稀疏线性组合同时稀疏表示。在JSM框架中,待测试像元与其邻域像元共享同一个稀疏模型并且邻域像元对中心像元有同等的贡献。在待测试像元分类过程中通过并入空间邻域信息,JSM分类方法能够实现很好的分类效果,然而,该算法对待测试中心像元邻域的像元均予以相同的权重,对于同构区域是非常合适的,对于异构区域就会导致错误的分类,尤其是边界部分。基于文献[11]提出联合稀疏模型框架思想,文献[12]提出一种联合鲁棒性稀疏表示分类算法,在联合稀疏模型的基础上充分利用残差波段中包含的特征信息对分类的影响,通过套索[13]莱斯塔特绝对收缩和选择算子(least absolute shrinkage and selection operator,LASSO)算法最优化稀疏系数与残差,从而分类待测样本。考虑到邻域像元的独特性,文献[14]提出了非局部权重联合稀疏表示分类(nonlocal weigth joint sparse representation classification, NLW-JSRC)算法,主要创新在于在邻域像元上引入非局部权重来反映中心测试像元与邻域像元的相关性。上述两种联合稀疏表示分类模型第一次定义中心测试像元周围的邻域像元为与其最近的n×n正方形内的邻域像元并且在中心测试像元所在的局部区同时联合稀疏表示中心像元与邻域像元来分类中心测试像元。JSM对邻域像元均予以相同的权重,而NLW-JSRC对不同邻域像元予以不同权重。此外,联合稀疏表示模型也经常被用于目标检测与生物识别等领域[15]。
基于NLW-JSRC算法的思想,提出基于核函数的联合稀疏表示分类方法。主要方法在于考虑到在中心测试像元分类过程中不同的邻域像元对其分类有不一样贡献。与以上两种联合稀疏模型不同之处在于对每个中心测试像元与其周围所有的邻域像元均求一次权重,然后取权重最大的T个不规则邻域像元为最优邻域窗口。本文采用3种核函数[16]来自适应对待测中心像元的邻域像元赋予权重。这种自适应加权方案不仅可以计算待测中心像元的局部邻域像元权重大小,还可以计算整个图像的邻域像元权重大小。
1 相关工作
1.1 JSRC
在高光谱图像,通常相邻像元由相似地物组成,它们存在极大的可能属于同一地物,因此可以共享同一个稀疏模型。假设有C类不同的地物,每类均有n个训练样本,则由所有训练样本组成的字典可以表示为A=[A1,A2,…,AC]∈RB×N,其中,B表示高光谱图像的光谱波段数;N为C类训练样本字典组成的训练样本总数;AC为第C类字典。待测中心像元与其邻域像元可以表示为Y=[y1,y2,…,yT]∈RB×T,其中,y1为待测的中心像元;其余像元为y1的邻域像元;T为待测中心像元与其邻域像元数量的总和。
因此在联合稀疏表示模型中,Y可以表示为
Y=[Aα1,Aα2,…,AαT]=AS
(1)
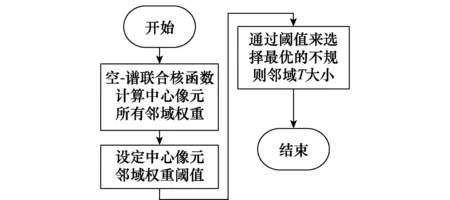
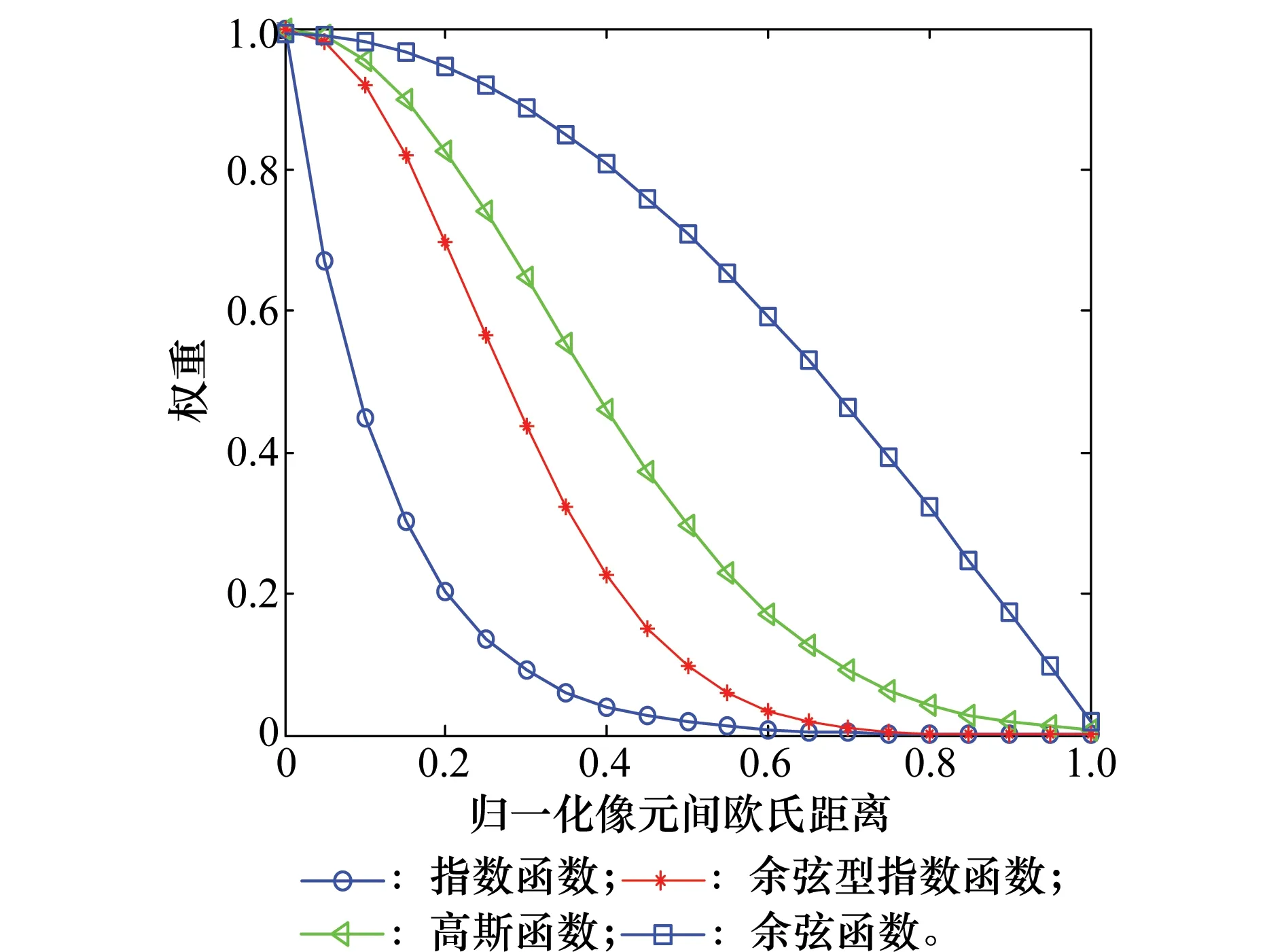
式中,S=[α1,α2,…,αT]∈RN×T为稀疏矩阵;ai(i∈[1,T])为只有K(K (2) 式中,‖·‖F表示Frobenius范数;‖S‖row,0表示S矩阵非零行的行数;K为稀疏系数的上限值。SOMP算法能够用于解决式(2)的优化问题。稀疏系数矩阵S可通过式(2)求得,则待测中心像元便可以根据重构残差被分类出来,其表达式为 (3) 在JSM中,在局部邻域内的像元均相似并被予以相同的权重。然而,不是所有的局部邻域像元都是同一类地物,尤其是图像边界地区由不同种类的地物组成。为了更好的区分邻域像元,文献[14]提出NLW-JSRC分类算法,其表达式为 (4) 式中,W=diag{w1,w2,…,wT}为对角权重矩阵。在论文中一种非局部权重联合稀疏表示分类算法被用于测量中心像元与邻域像元的相似度。 在JSRC分类算法中,利用像元间的空间位置信息,即相邻像元具有相似性,可以共享同一稀疏模型,从而建立一个JSM。在NLW-JSRC分类算法中,基于JSM框架提出非局部权重思想,充分利用邻域像元间的相似性与独特性。文献[9]提出的联合核函数表示方法计算邻域像元权重的基础上,提出一种改进核函数的联合稀疏表示分类算法。算法主要创新在于将测量像元空间信息的核函数与测量像元光谱信息的核函数以一定比例结合并采用JSM框架来联合稀疏表示分类,即相邻且相似的像元共用同一稀疏表示模型来进行地物的分类。最终根据改进的联合核函数计算待测中心像元与邻域像元的权重来自适应的选择每个待测像元的最优邻域。核函数的选择如文献[16]所示的3种核函数,其表达式为 (5) 式中,Ep,q、Gp,q、Cp,q分别为指数核函数、高斯核函数、余弦核函数,其中xp、xq、μd分别表示待测中心像元的像素坐标、邻域像元的像素坐标、像素空间距离标准差,μd的求解由文献[9]可知。式(5)中的3种核函数用于计算待测中心像元与邻域像元空间距离权重。 在高光谱图像中,由于每种地物边界部分均可能存在多种其混合地物以及基于测量空间距离的核函数K对距离待测中心像元较近的地物会赋予较大的权重而造成类别的错分。针对以上问题本文提出对空间距离权重K与光谱距离权重GS(p,q)予以1:λ(λ>0)的比重,其表达式为 (6) wp,q=K*GS(p,q) (7) 式(6)中,GS(p,q)表示待测中心像元与邻域像元的光谱相似权重;xp、xq、μs分别表示待测中心像元光谱值、邻域像元光谱值以及光谱标准差;μs亦可由文献[9]得知。式(7)中,wp,q是由两种核函数结合,即空间距离与光谱距离结合并用于度量待测中心像元与邻域像元的相似性,即计算邻域权重。当权重wp,q小于某一阈值δ(0<δ)时,像元xp与xq属于不同地物,当权重wp,q大于δ时,像元xp与xq权重为wp,q。因此,采用文献[14]提出的权重改善方案,并在此基础上进行改进,其表达式为 (8) 通过式(6)~式(8)计算得到的权重Wp,q可以计算出每个待测中心像元的最优邻域T,求每个待测中心像元邻域大小的基本流程如图1所示。 图1 联合核函数算法流程图Fig.1 Block diagram of combined kernel function 由图1可知,该算法不同于JSRC分类算法和NLW-JSRC分类算法均以待测试像元为中心取周围的n×n像元作为邻域窗口大小,而是通过联合核函数算法计算每个待测中心像元的邻域像元权重来选择邻域窗口,窗口是不规则且大小不同,并且每个邻域窗口大小都是此算法下最优邻域。 根据两个数据集地物分布的特点:Indian Pines数据集的地物比较集中,而University of Pavia相对分散。测量距离权重选择高斯核函数对University of Pavia数据集分类比较合适,而指数核函数对Indian Pines数据集分类较为合适,通过文献[16]对3种核函数进行了分析,提出将指数型核函数与余弦型核函数结合来强化高斯核函数加权不足和弱化指数型核函数过度加权,其表达式为 (9) KK表示两种核函数结合后的空间距离核函数,即余弦型指数核函数。KK与其他核函数的曲线图如图2所示。 图2 4种核函数权重曲线图Fig.2 Weight curves of four kinds of kernel functions 分析图2可知,随着像元之间的欧氏距离增大,指数核函数下降很快以至于加权过重,高斯核函数和余弦核函数的曲线下降得较为缓慢。而本文改进的余弦型指数核函数在距离较小时权重很大,随着距离的增大而权重减小,余弦型指数核函数的这一特点弥补了高斯型核函数加权不足而指数型核函数加权过度的缺点。 通过分析,将式(7)转化成式(10)为 (10) 式中,权重wp,q可以通过如上3种联合核函数求得,基于光谱与空间距离的联合核函数的联合稀疏表示分类算法的基本模型如式(4)所示。其中W=diag{w1,w2,…,wT}为对角权重矩阵,它的对角元素wp,q表示周围邻域像元对中心像元xp贡献的大小即权重,权重Wp,q如式(10)所示。通过以上权重公式计算出每个待测中心像元与周围所有邻域像元权重Wp,q的大小来选择最优的邻域T的大小,最终通过JSM计算出如下所示的重构残差来分类中心测试像元y为 (11) 将上述基于JSM算法框架而改进联合核函数联合稀疏表示分类算法的具体流程总结成如算法1所示。 算法1基于核函数的联合稀疏表示分类算法 输入在每类地物中随机选取同样大小样本组成训练类字典A=[A1,A2,…,AC] 初始化初始归一化字典A For高光谱图像中的每个像元y: (2) 构建联合信号矩阵Y=[y1,y2,…,yT]∈RB×T,并且归一化联合信号矩阵Y; (3) 通过式(4)计算系数稀疏矩阵S; (4) 通过式(10)计算残差r,并标记测试样本y; (5) 返回下一个待测像元。 End For 输出一个所有像元均带标签的二维矩阵 Indian Pines:Indian Pines图像是在1992年通过AVIRIS传感器获得的。图像大小为145×145个像素,共有220个波段,把其中水吸收和噪声波段去掉,最终剩下200个波段,获得的数据共包含16个类别。本次实验集选取其中的9个样本较多的类进行分类实验。这9类分别为:免耕玉米(Corn-notill),少耕玉米(Corn-mintill),草牧场(Grass-pasture),草树(Grass-trees),干草匀堆料(Hay-windrowed),免耕大豆(Soybean-notill),少耕大豆(Soybean-mintill),净耕大豆(Soybean-clean),木材(Woods)。 University of Pavia:University of Pavia图像是在2001年通过ROSIS传感器获得的,图像大小为610×340个像素,共有115个波段,除去其中水吸收和噪声波段去掉,剩下其中103个波段,该图像总共包含9个类别地物分别为:沥青(Asphalt),草地(Meadows),砾石(Gravel),树(Trees),金属板材(Painted metal sheets),裸露土壤(Bare Soil),柏油屋顶(Bitumen),自挡砖(Self-Blocking Bricks),阴影(Shadows)。 仿真实验在主频3.7 GHz,内存8 GB的PC机上进行,操作系统为Window(64位),仿真平台为Matlab2014a(64位)。本文提出的核函数联合稀疏表示(K-JSRC)算法对比于其他算法,例如NLW-JSRC、SOMP、SRC、SVM算法。本文将在Indian Pines和University of Pavia两个数据集上进行不同的仿真对比。在Indian Pines数据集上,通过对比几组在训练样本大小不同的条件下的总体分类精度、Kappa系数(K)来评估算法的分类性能。在University of Pavia数据集上,通过对比每类的分类精度、总体分类精度、Kappa系数(K)来评估算法的分类性能。 参数设置:在Indian Pines数据集中NLW-JSRC、JSRC、SRC训练样本的大小的取值如表1所示。SVM算法中的RBF核的γ值设置为高光谱数据维度的倒数,正则化参数c实验时设置为林智仁教授libsvm工具包中的默认参数1。由文献[11,14]可知,JSRC算法与NLW-JSRC算法的最优邻域大小T为5×5和9×9。 图3 University of Pavia数据集上参数λ对总体分类精度的影响Fig.3 Effects of upper parameters λ on the overall classification accuracy of the 图4 University of Pavia数据集上参数w1和w2对总体分类精度的影响 Fig.4 Effects of upper parameters w1 and w2 on the overall classification accuracy of the University of Pavia dataset 在Indian Pines数据集上,通过5组在不同训练样本的精度对比,每类训练样本均随机选,其余作为测试样本。在University of Pavia数据集上,我们在每类原子中随机选取30个作为训练样本,其余为测试样本。实验重复10次取平均值,在两个数据集上的实验结果如表1和表2所示。 对比表1与表2分类结果和图5与图6的分类效果可知,我们可以得出如下几点结论: (1) 在两个数据集上,对比于其他算法,本文提出的3种K-JSRC算法展现了更好的分类效果,而其中CEK-JSRC算法在3种K-JSRC算法中分类效果最好。从效果图也能看出本文提出的核算法分类效果最好,由于CEK-JSRC算法只比其他两种核函数算法的精度高1至2个百分点,所以效果图并不是很明显,但相对其他对比算法还是要明显一些。 (2) 在Indian Pines数据集上EK-JSRC算法的分类精度要好于GK-JSRC算法,而在University of Pavia数据集上要差于GK-JSRC算法。主要原因在于Indian Pines数据集上地物更集中,在一定的邻域范围内,距离待测中心像元越近权重越大更有利于提高分类精度,而University of Pavia数据集上的地物较之为分散。 (3) 基于空间-光谱的分类算法(JSRC,NLW-JSRC,K-JSRC)明显要优于基于光谱分类算(OMP,SVM)。 (4) 对比JSRC算法,本文提出K-JSRC算法加入了光谱权重,对邻域像元特别是边界的不同地物像元的判别有了很大改进。对比于NLW-JSRC算法,本文提出的3种K-JSRC算法对每个待测像元求邻域权重和最优邻域大小,因此,K-JSRC算法分类精度要于NLW-JSRC算法和JSRC算法。 表1 Indian Pines数据集分类精度 图5 Indian Pines数据集分类结果Fig.5 Classification result in Indian Pines data set 类#样本训练测试分类算法SVMOMPJSRCNLW⁃JSRCK⁃JSRCGaussianExponentialCosineExponentialAsphalt30663176.1556.6788.3787.5991.5592.1193.09BareSoil301864972.0668.8980.5188.9382.0480.9391.46Bitumen30209970.4265.5488.6179.3679.7078.8397.44Bricks30306493.3092.0980.8286.3593.9493.2495.39Gravel30134599.1199.391199.7099.8599.75Meadows30502984.2463.3976.5178.8497.2897.3477.14Metalsheets30133091.7883.8595.2480.4699.4699.8599.00Shadows30368279.3461.9454.6845.9569.1765.9949.14Trees3094799.7890.0865.5477.2183.8682.7794.77总体分类精度/%78.6670.1081.6084.0287.3686.7988.41稀疏度K71.0660.5474.5876.2779.9780.7181.93 图6 University of Pavia数据集分类结果Fig.6 Classification result University of Pavia data set 本文提出的基于核函数的联合稀疏表示分类算法改善了JSRC算法对边界像元分类不完全及NLW-JSRC算法未充分挖掘每个待测像元的最优邻域像元的不足。改进传统核函数对权重计算上的不足,引入余弦型高斯核函数来改善权重,测量每个待测中心像元邻域像元相似度并自适应的得到每个待测中心像元最优邻域T的大小。在两个数据集上的仿真实验结果表明,该算法在精度与稳定性上要优于同类算法与传统的分类算法。但是,研究工作还有几处待改进的地方,例如,如何进一步优化权重与比重,如何进一步增强算法的自适应性和稳定性等。 [1] FARID M, LORENZO B. Classification of hyperspectral remote sensing images with support vector machines[J]. IEEE Trans.on Geoscience and Remote Sensing, 2004, 42(8): 1778-1790. [2] BOR-CHEN K, HSIN-HUA H, Hsuan C A. Kernel-based feature selection method for SVM with RBF kernel for hyperspectral image classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(1): 317-320. [3] GUSTAVO C V, LORENZO B. Kernel-based methods for hyperspectral image classification[J]. IEEE Trans.on Geoscience and Remote Sensing, 2005, 43(6): 1351-1362. [4] LIU T Z, GU Y F, JIA X P, et al. Class-specific sparse multiple kernel learning for spectral-spatial hyperspectral image classification[J]. IEEE Trans.on Geoscience and Remote Sensing, 2005, 43(6): 1351-1362. [6] ZHANG B, LAN T, HUANG X, et al. Spatial-spectral kernel sparse representation for hyperspectral image classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2013, 6(6): 2462-2471. [7] LI W, DU Q. Adaptive sparse representation for hyperspectral image classification[C]∥Proc.of the IEEE Geoscience and Remote Sensing Symposium, 2015: 4955-4958. [8] JIA S, ZHANG X, LI Q. Spectral-spatial hyperspectral image classification using, regularized low-rank representation and sparse representation-based graph cuts[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2015, 8(6): 2473-2484. [9] WANG Z, NASRABADI N M, HUANG T S. Semisupervised hyperspectral classification using task-driven dictionary learning with laplacian regularization[J]. IEEE Trans.on Geoscience & Remote Sensing, 2015, 53(3): 1161-1173. [10] XIONG M, RAN Q, et al. Hyperspectral image classification using weighted joint collaborative representation[J]. IEEE Geoscience & Remote Sensing Letters,2015,12(6):1209-1213. [11] CHEN Y, NASRABADI N M, TRAN T D. Hyperspectral image classification using dictionary-based sparse representation[J]. IEEE Trans.on Geoscience & Remote Sensing, 2011, 49(10): 3973-3985. [12] LI C, MA Y, MEI X, et al. Hyperspectral image classification with robust sparse representation[J]. IEEE Geoscience & Remote Sensing Letters, 2016, 13(5): 641-645. [13] TIBSHIRANI R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society, 1996, 58(3): 267-288. [14] ZHANG H, LI J, HUANG Y, et al. A nonlocal weighted joint sparse representation classification method for hyperspectral imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2014, 7(6): 2056-2065. [15] SHEKHAR S, PATEL V M, NASRABADI N M, et al. Joint sparse representation for robust multimodal biometrics recognition[J]. IEEE Trans.on Pattern Analysis & Machine Intelligence, 2014, 36(1): 113-126. [16] TIAN J, YU W Y, XIE S L. On the kernel function selection of nonlocal filtering for image denoising[C]∥Proc.of the IEEE International Conference on Machine Learning and Cybernetics, 2008: 2964-2969. [17] ZHANG L, ZHOU W D, CHANG P C, et al. Kernel sparse representation-based classifier[J]. IEEE Trans.on Signal Processing, 2012, 60(4): 1684-1695.
1.2 NLW-JSRC
2 K-JSRC
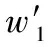

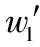
3 实验与讨论
3.1 数据集
3.2 算法的对比与参数的设置




3.3 分类结果




4 结 论
