舰载机着舰纵向非仿射模型控制器设计
2018-03-14吴文海胡云安
张 杨, 吴文海, 胡云安, 高 丽
(1. 海军航空工程学院青岛校区航空仪电控制系, 山东 青岛 266041; 2. 海军航空工程学院控制工程系, 山东 烟台 264001)
0 引 言
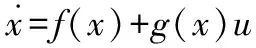
而现在大多数处理非仿射模型方法都是将非仿射模型转换为仿射模型。文献[9-10]普遍采用泰勒公式和中值定理将非仿射模型转换为仿射模型,然后再针对仿射型系统设计控制器。由于这种方法直接忽略了高阶项,难免产生较大的误差。并且之前大多数是对控制理论或传统飞控进行研究,而在舰载机着舰领域的非仿射研究方案少之又少。
本文针对舰载机着舰模型提出了基于非仿射预设性能的控制律方法,该方法在传统反演方法基础上进行设计,但是无需对中间控制求导,也无需引入动态面等方法得到中间控制器的高阶导数,简化了设计过程;而且不需要自适应估计或者神经网络等方法对未知函数近似,这无疑降低了控制器设计的复杂度;同时对模型的不确定性及外部的舰尾流扰动有较强的鲁棒性。
1 舰载机着舰非仿射模型
舰载无人机非线性数学模型[11]为
g(cosφcosθsinαcosβ+sinφ
cosθsinβ-sinθcosαcosβ)+
(1)
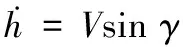
(2)
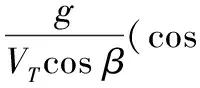
(3)
Lcosμ+Ft(cosμsinα+sinμsinβcosα)-mgcosγ]
(4)
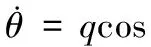
(5)
(6)
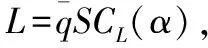
δ2+
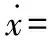
该纵向着舰非仿射纯反馈模型为
(7)
式中,gh(γ)、gγ(h,γ,θ)、gθ(q)、gα(α,γ,q)、gq(h,γ,δ)是未知非线性连续函数。
2 纵向控制器设计
定义1连续函数ρ(t):R+→R+称为性能函数,并且同时满足以下两个条件:
(1)ρ(t)为正且严格递减;
(2) limt→∞ρ(t)=ρ∞>0.
控制目标(2)可以通过如下不等式实现:
-Mρ(t)
(8)
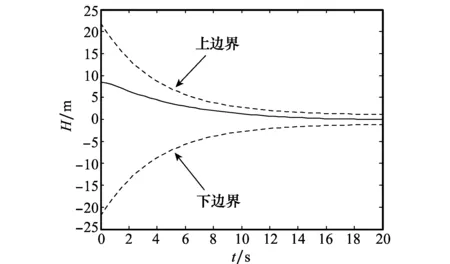
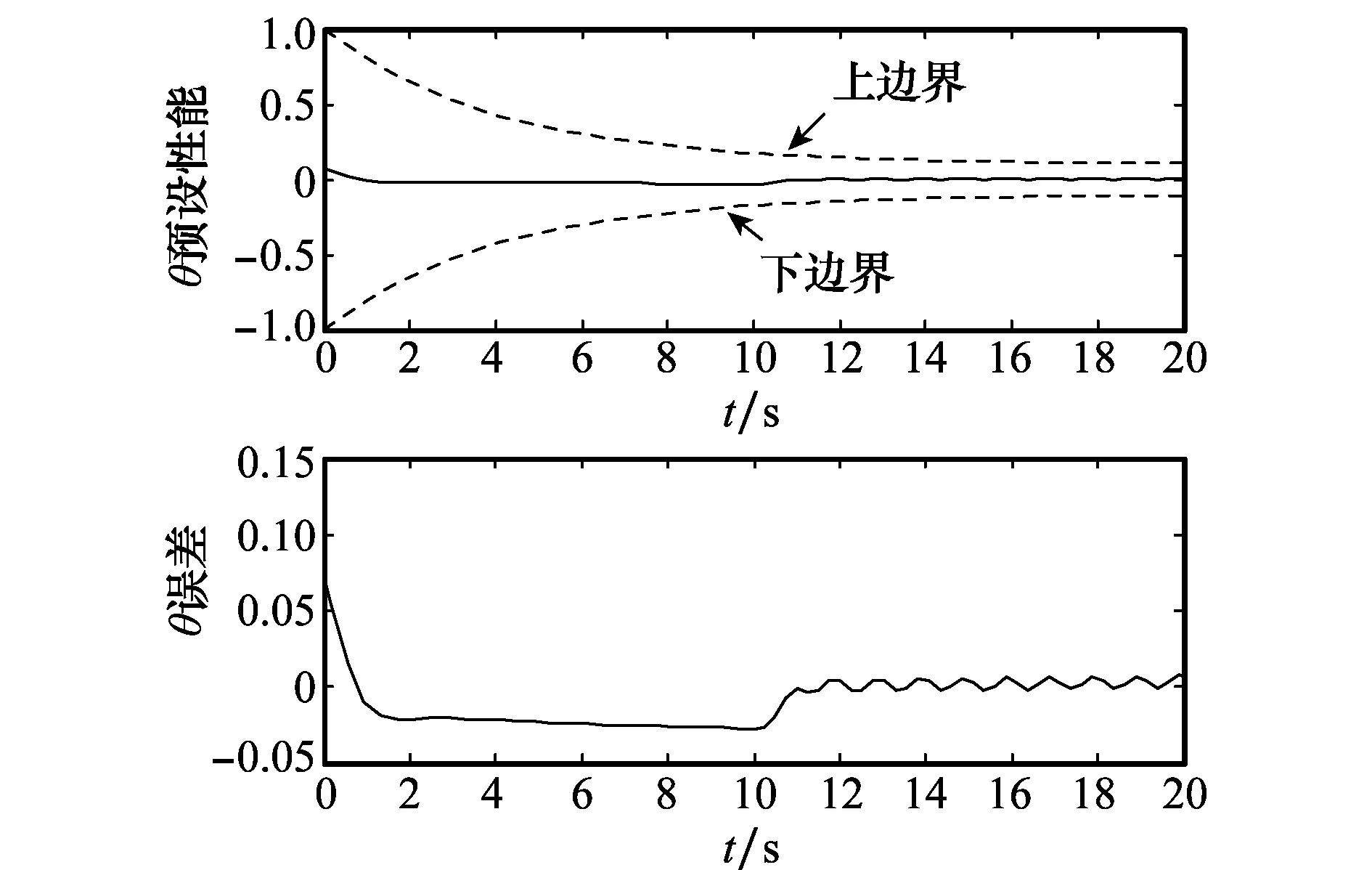
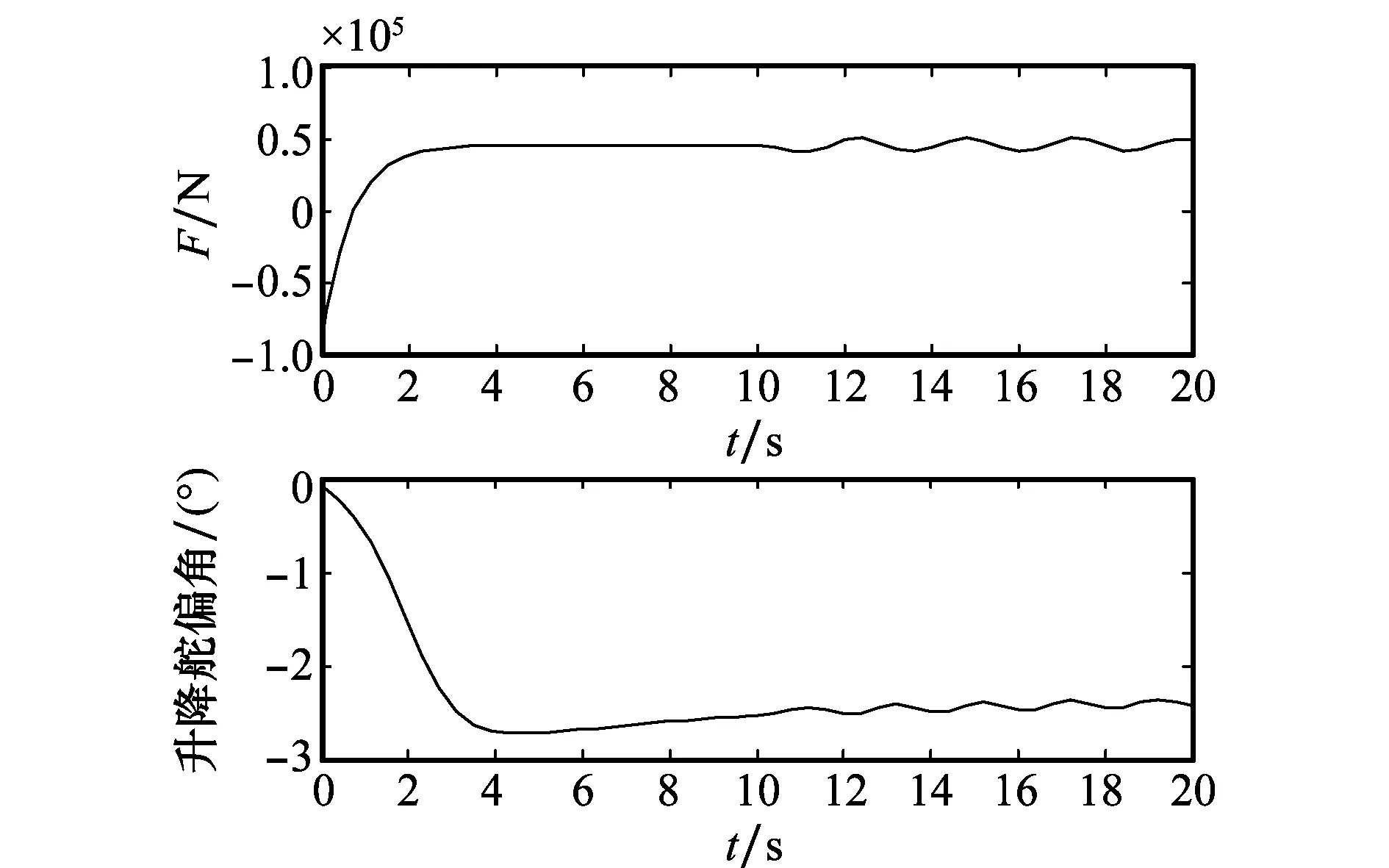
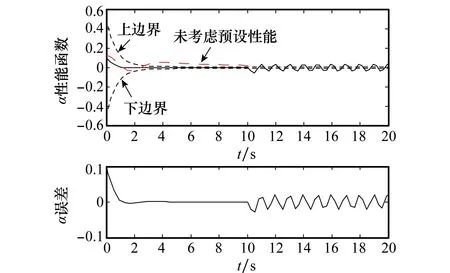
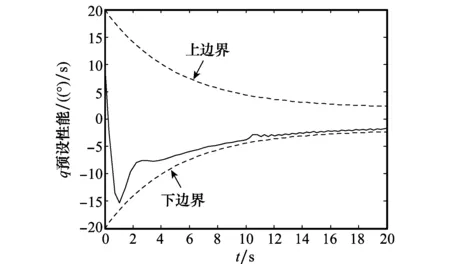
-ρ(t) (9) 其中,M∈[0,1]为设计参数。本文设计思路主要参考文献[15],令M=1,进一步得到e(t)∈(-ρ(t),ρ(t)),∀t≥0。性能函数取为ρ(t)=(ρ0-ρ∞)e-lt+ρ∞,ρ0>ρ∞>0,l>0。预设性能曲线图如图1所示。其中常数ρ∞表示预先设定的稳态误差的上界,ρ(t)的衰减速度为跟踪误差e(t)收敛速度的下界,同时跟踪误差的最大超调不会大于ρ(0)。因此,通过选择适当的性能函数ρ(t)便可对输出误差的稳态和瞬态性能进行限制。 图1 预设性能曲线Fig.1 Prescribed performance curve 假设1目标高度函数连续有界且已知,一阶导数连续有界但未知。 由于目标(高度、姿态角等)通过卫星或雷达引导可以实时测得,然而其导数并不是可直接获得的数据,因此假设一阶函数相关信息未知。 假设2存在未知正常数使得 由于构建的舰载机非仿射模型连续并可导有界,因此可知假设2成立。 本文控制器设计目标: (1) 设计控制器使所有信号有界,系统全局稳定; (2) 高度、俯仰角、迎角和俯仰角速率等跟踪误差满足预先设定的性能。 设计控制器之前首先定义转换函数,即 ρ1(0)>|x1(0)-hc(0)| ρ1(t)>(ρ10-ρ1∞)e-k1t+ρ1∞ 式中,ρ10>ρ1∞>0;k1>0。 定义转换误差及控制律设计。预设性能的一个重要步骤便是重新定义转换误差,即 因此,设计第1步的虚拟控制律 (10) ρ2(0)>|x2(0)-γc(0)| ρ2(t)>(ρ20-ρ2∞)e-k2t+ρ2∞ 式中,ρ20>ρ2∞>0;k2>0。 定义转换误差及控制律设计。类似步骤1,通过转换误差可得 设计第2步虚拟控制律 (11) ρ3(0)>|x3(0)-θc(0)| ρ3(t)>(ρ30-ρ3∞)e-k3t+ρ3∞ 式中,ρ30>ρ3∞>0;k3>0。 定义转换误差及控制律设计。通过转换误差函数,可得 设计第3步虚拟控制律 (12) ρ4(0)>|x4(0)-qc(0)| ρ4(t)>(ρ40-ρ4∞)e-k4t+ρ4∞ 式中,ρ40>ρ4∞>0;k4>0。 定义转换误差及控制律设计。通过转换误差,可得 设计第4步虚拟控制律 (13) ρ5(0)>|x5(0)-qc(0)| ρ5(t)>(ρ50-ρ5∞)e-k5t+ρ5∞ 式中,ρ50>ρ5∞>0;k5>0。 定义转换误差及控制律设计。与之前步骤相似,可得 设计最后一步实际控制律 (14) 由上文设计的控制器形式可知,该控制器不需要已知系统非线性项的相关参数,或者是函数的上下界,也不需要对未知非线性进行估计。并且和传统反演不同的是,不需要中间虚拟控制的高阶导数,减少了控制器设计的复杂度。 定理1考虑闭环非仿射系统(7),在假设1、假设2的前提下,给定任意初始条件xi(0),i=1,2,3,4,5,设计的控制器(10)~(14),使得系统全局稳定,所有信号有界并且跟踪误差满足预先设定的性能。 证明 则 (15) 由 (16) 可得 ζ1(t,χ1,χ2) (17) 同理,可得 ζ2(t,χ1,χ2,χ3) (18) ζ4(t,χ1,χ2,χ3,χ5) (19) ζ4(t,χ1,χ2,χ3,χ4,χ5) (20) (21) 由以上可得集合为 (22) 并定义开集为 Ωχ=(-1,1)×(-1,1)×(-1,1)×(-1,1)×(-1,1) 由定理1可知,式(22)存在唯一最大值使得Χ:[0,τmax)→Ωχ。因此对于所有的t∈[0,τmax),闭环系统所有信号有界,并且对于所有的t∈[0,τmax),Χ严格在开集Ωχ范围内。即 χ1(t)∈(-1,1),χ2(t)∈(-1,1),χ3(t)∈(-1,1), χ4(t)∈(-1,1),χ5(t)∈(-1,1) 将式(17)~式(21)代入式(15)得到 [gγ(χ1(t)ρ1(t)+hc,χ2(t)ρ2(t)+γc, [gα(χ4(t)ρ4(t)+αc,χ2(t)ρ2(t)+γc, (23) 由假设2并结合平均值定理可得 gh(χ2(t)ρ2(t)+γc)= (24) 同式(24)类似可得 gγ(χ1(t)ρ1(t)+hc,χ2(t)ρ2(t)+γc, χ3(t)ρ3(t)+θc)=gγ(χ1(t)ρ1(t)+hc, χ2(t)ρ2(t)+γc,χ3(t)ρ3(t))+ (25) (26) gα(χ4(t)ρ4(t)+αc,χ2(t)ρ2(t)+γc, χ5(t)ρ5(t)+qc)=gα(χ4(t)ρ4(t)+αc, χ2(t)ρ2(t)+γc, (27) gq(χ1(t)ρ1(t)+hc,χ2(t)ρ2(t)+γc,δ))= gq(χ1(t)ρ1(t)+hc,χ2(t)ρ2(t)+γc,0)+ (28) 将式(24)~式(28)代入式(23),进一步可得 χ2(t)ρ2(t)+γc,χ3(t)ρ3(t))-a2ε2(t)· χ2(t)ρ2(t)+γc,χ5(t)ρ5(t))- (29) 假设2进一步可以表示为 由式(29)进一步可得 χ2(t)ρ2(t)+γc,χ3(t)ρ3(t))- χ2(t)ρ2(t)+γc,χ5(t)ρ5(t))- (30) 另外,由 (gγ(χ1(t)ρ1(t)+hc,χ2(t)ρ2(t)+γc, (gα(χ4(t)ρ4(t)+αc,χ2(t)ρ2(t)+γc, |gγ(χ1(t)ρ1(t)+hc,χ2(t)ρ2(t)+γc, |gα(χ4(t)ρ4(t)+αc,χ2(t)ρ2(t)+γc, |gq(χ1(t)ρ1(t)+hc,χ2(t)ρ2(t)+γc,0)- (31) 由式(31)可知,当 Ω=Ωε1(t)∪Ωε2(t)∪Ωε3(t)∪Ωε4(t)∪Ωε5(t) 其中 为进一步分析跟踪误差在预设性能,引入引理1。 引理1如果转换误差函数ε(t)有界并且存在常数εB>0使得|ε(t)|≤εB,那么误差e(t)∈(-ρ(t),ρ(t))。 证明 结合引理1可得 定理1得证。 证毕 本文设计的方法不需要类似传统反演方法对中间控制变量进行求导,避免了“指数膨胀”问题,减少了计算量;并且控制器设计过程不需要着舰的精确模型;同时对于模型的不确定性有较强的鲁棒性,不需要自适应估计或者采用神经网络和模糊控制等方法来对模型进行近似。 着舰时需要考虑舰尾流的影响,本文采用的是目前运用较多的军标MIL-HDBK-1797中[16]描述的舰尾流模型,包括雄鸡尾流、尾流随机分量、周期分量和随机自由大气紊流分量。 参数设置及初始值为 V0=50 m/s Vr=70 m/s,H(0)-Hr(0)=8 m α(0)=0.1,γ(0)=0,θ(0)=0.2,q(0)=8 a1=1,a2=0.1,a3=0.3,a4=3,a5=10 预设性能函数为 ρ1(t)=(22-1)e-0.25t+1 ρ2(t)=(0.6-0.02)e-0.5t+0.02 ρ3(t)=(1-0.1)e-0.25t+0.1 ρ4(t)=(0.5-0.01)e-1.5t+0.01 ρ5(t)=(20-2)e-0.2t+2 舰载机高度误差随时间变化的曲线如图2所示。 图2 高度跟踪误差Fig.2 Error of height tracking 由图2可知,误差曲线在预先设定的范围内,并且误差收敛较快。 舰载机俯仰角误差随时间变化的曲线如图3所示。 图3 俯仰角误差及预设性能Fig.3 Pitch error and prescribed performance 由图3可知,采用预设性能方法后使误差在0.1的范围内进行变化,并在预先设定的范围内,在实际飞行过程中这样的俯仰角跟踪精度较高。本文设计的方法提供了快速准确的俯仰角响应,尽管在10 s后加入了舰尾流扰动,但是跟踪误差仍然较小,具有较高的鲁棒性能。 设计的舵偏角和推力控制曲线如图4所示。 图4 推力升降舵曲线Fig.4 Thrust and elevator curve 由图4可知,尽管扰动加入使得控制器设计出现波动,但是即使在存在舰尾流扰动的情形下,升降舵偏角依然保持波动较小。 迎角误差随时间变化的曲线如图5所示。 图5 迎角误差考虑预设性能和未考虑预设性能对比图Fig.5 Comparison chart of considering prescribed performance and without prescribed performance 为了进一步分析本文方法的优越性,本文和未考虑预设性能的迎角跟踪误差曲线进行了对比,由图5可知,考虑性能函数的误差较大,没有在预先设定的范围内。 俯仰角速率误差跟踪曲线如图6所示。 图6 俯仰角速率跟踪误差曲线Fig.6 Pitching angular rate tracking error curve 俯仰角速率误差在开始的2 s较大,但是跟踪误差收敛较快且在预先设定的要求范围之内。从图2、图3、图5、图6可知,误差曲线在预先设定的范围内,满足预先设计的要求。 速度控制曲线如图7所示。 图7 速度控制曲线Fig.7 Curve of velocity 由图7可知,设计的控制器能快速地跟踪期望的设定速度且跟踪误差较小。 综合以上图分析,尽管10 s加入了舰尾流扰动,但是控制器鲁棒性能较好,采用预设性能方法的误差都在预先设定的范围内,并且满足快速性和鲁棒性。 针对舰载机着舰模型中更为一般的非仿射非线性模型进行了控制律的设计,提出了非仿射着舰纵向预设性能控制器方法。从理论推导看出该方法无需对中间控制变量求导,避免了“指数膨胀”问题,减少了计算量;简化了设计过程,控制器更加简单,不需要神经网络或者模糊控制器对未知参数进行估计;考虑了舰尾流外部扰动,鲁棒性较高。通过仿真证明了该方法的有效性和正确性。 [1] 朱齐丹, 孟雪, 张智. 基于非线性动态逆滑模的纵向着舰系统设计[J]. 系统工程与电子技术, 2014, 36(10): 2037-2042. ZHU Q D, MENG X, ZHANG Z. Design of longitudinal carrier landing system using nonlinear dynamic inversion and sliding mode control[J]. Systems Engineering and Electronics, 2014, 36(10):2037-2042. [2] 郑峰婴, 龚华军, 甄子洋. 基于积分滑模控制的无人机自动着舰系统[J]. 系统工程与电子技术, 2015, 37(7): 1621-1628. ZHENG F Y, GONG H J, ZHEN Z Y. Carrier UAV autonomous landing system based on integral sliding mode control[J]. Systems Engineering and Electronics, 2015, 37(7):1621-1628. [3] 黄得刚,章卫国,邵山,等.舰载机自动着舰纵向控制系统设计[J]. 控制理论与应用, 2014(12): 1731-1739. HUANG D G, ZHANG W G, SHAO S, et al. Design of automatic control system for longitudinal landing on carrier[J]. Control Theory & Applications, 2014(12):1731-1739. [4] ZHANG Y, WU W, WANG J, et al. Prescribed performance adaptive constrained backstepping controller for carrier-based longitudinal landing with magnitude constraints[C]∥Proc.of the China Control Conference, 2017: 856-861. [5] ZHENG F Y, GONG H J, ZHEN Z Y. Adaptive constraint backstepping fault-tolerant control for small carrier-based unmanned aerial vehicle with uncertain parameters[J]. Proceedings of the Institution of Mechanical Engineers Part G: Journal of Aerospace Engineering, 2016, 230(3), 407-425. [6] LEE T, KIM Y. Nonlinear adaptive flight control using backstepping and neural networks controller[J]. Journal of Guidance Control & Dynamics, 2001, 24(4): 675-682. [7] BOSKOVIC J D, CHEN L, MEHRA R K. Multivariable adaptive controller design for a class of non-affine models arising in flight control[C]∥Proc.of the IEEE Conference on Decision and Control,2001:2442-2447. [8] 刘鑫燕. 高超声速无人机的非仿射模糊滑模控制研究[D]. 南京:南京航空航天大学, 2014. LIU X Y. Research on fuzzy sliding mode control for hypersonic unmanned aerial vehicle[D]. Nanjing:Nanjing University of Aeronautics and Astronautics,2014. [9] CHEN L, WANG Q. Adaptive robust control for a class of uncertain MIMO non-affine nonlinear systems[J]. IEEE/CAA Journal of Automatica Sinica, 2016, 3(1): 105-112. [10] BOSKOVIC J D, CHEN L, MEHRA R K. Adaptive control design for nonaffine models arising in flight control[J]. Journal of Guidance Control & Dynamics, 2004, 27(2): 209-217. [11] FITZGERALD. Flight control system design for autonomous UAV carrier landing[D]. England: Cranfield University, 2004. [12] ZHENG F Y, ZHEN Z Y, GONG H. Observer-based backstepping longitudinal control for carrier-based UAV with actuator faults[J]. Journal of Systems Engineering and Electronics, 2017, 28(2):322-337. [13] GAVILAN F, VAZQUEZ R, ACOSTA J. Adaptive control for aircraft longitudinal dynamics with thrust saturation[J]. Journal of Guidance Control & Dynamics, 2014, 38(4): 651-661. [14] 张杨, 胡云安. 受限指令预设性能自适应反演控制器设计[J]. 控制与决策, 2017,32(7):1253-1258. ZHANG Y, HU Y A. Prescribed performance adaptive backstepping controller design based on constrained command filtered[J]. Control and Decision, 2017, 32(7):1253-1258. [15] BECHLIOULIS C P, ROVITHAKIS G A. A low-complexity global approximation-free control scheme with prescribed performance for unknown pure feedback systems[J]. Automatica, 2014, 50(4): 1217-1226. [16] MIL-F-8785 C Military specification:Flying qualities of piloted airplanes[S].Washington D.C.:Department of Defense, 1980.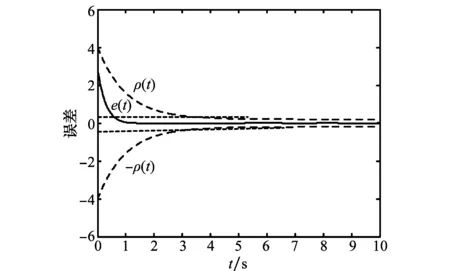
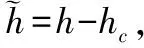
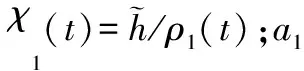
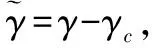
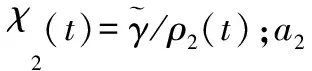
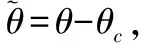
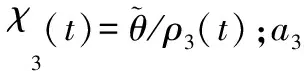
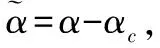

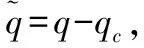
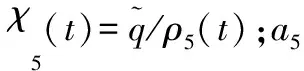
3 稳定性证明
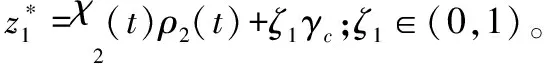
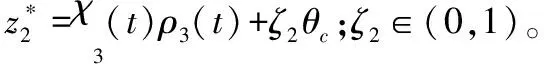
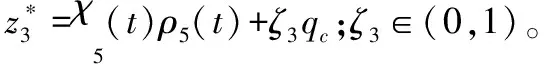
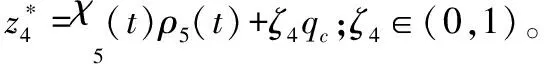
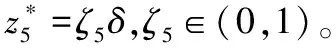
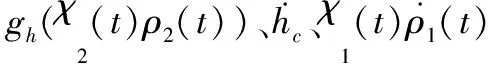
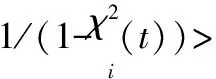
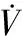
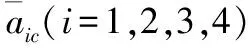
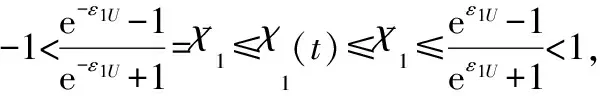
4 仿真分析验证

5 结 论
