鲁棒增益调度结构化火箭弹控制系统设计

郭致远, 姚晓先, 张 鑫

(北京理工大学宇航学院, 北京 100081)

0 引 言

火箭弹大多是尾翼稳定的低速旋转弹,具有反应时间短、火力猛、威力大等优势,然而,其散布随射程成倍增加。在常规弹药制导化的发展趋势下,火箭弹的低成本、简易控制受到了越来越多的关注[1]。无控火箭弹的落点散布主要取决于主动段的扰动[2]。火箭弹较难控制的一个原因在于其模型的时变特性和不确定性。对于无动力飞行段,与传统导弹类似,速度和空气密度都是对模型影响较大的因素;而对于续航段而言,尽管推力可以近似保持速度恒定,然而实际发动机所提供的推力也是变化的,此外,发动机提供推力的同时也会引起质量、质心和转动惯量等的变化。

目前的研究多集中在无动力飞行,发动机推力的存在会加剧火箭弹数学模型的不确定性和时变性。文献[3]和文献[4]分别基于状态依赖黎卡提方程(state-dependent Riccati equation, SDRE)和智能特征结构配置方法(intelligent eigenstructure assignment, IEA)设计了火箭弹的姿态控制器,这类控制器的设计均依赖于状态反馈,但是,在火箭弹的飞行过程中,部分状态变量难以测量和估计。文献[5]基于推力矢量控制(thrust vector control, TVC),使用反馈线性化和SDRE设计了火箭弹的姿态控制器。文献[6]通过离散自适应滑模设计了制导炸弹的解耦控制器。文献[7]基于鲁棒非线性反演控制方法设计了应对高灵敏度空空导弹强非线性和不确定性的控制器,然而该控制器的实现较为复杂。

增益调度控制是应对被控系统时变特性常见的控制器设计方案[8-9]。首先，将被控对象在各个工作点处线性化,将非线性、参数摄动、不确定性动力学作为模型不确定性,通过线性控制器综合方法设计各点的控制器,然后通过插值或其他方式将独立控制器综合起来,得到全局控制器,最后通过仿真验证控制器的稳定性和性能。文献[10]将高度作为调度变量,结合传统频域控制理论设计了用于末制导的火箭弹自动驾驶仪。文献[11]将时间作为调度变量,结合协同进化增广拉格朗日方法得到优化的控制器参数。文献[12]将速度和高度作为调度变量,使用鲁棒增益调度方法设计了炮弹的自动驾驶仪,控制器具有比例-积分的结构,易于在工程应用中实现。

本文以122 mm单室双推力火箭弹作为研究对象,使用常规线性鸭舵作为执行机构,建立了该火箭弹包含参数摄动的以线性分式变换(linear fractional transformation, LFT)描述的线性变参数(linear parameter varying, LPV)模型。对该火箭弹使用鲁棒增益调度技术设计了具有固定控制器结构的自动驾驶仪,利用定高飞行的设计目标在续航段将调度空间简化为时间-速度域,在无动力飞行段将调度空间简化为速度域,通过结构奇异值(structure singular value, SSV)分析了闭环系统在各特征点参数摄动情况下的鲁棒稳定性,并仿真验证了闭环系统的全局稳定性。

1 火箭弹动力学建模

本文所研究的火箭弹是轴对称型,具有两对线性鸭舵,呈“十”字布局,因此在滚转通道不可控。依据文献[13]中建立低速旋转弹动力学模型所用的坐标系统,建立了火箭弹的动力学模型,其中,火箭弹法向加速度表达式在弹道坐标系下为

(1)

其中

(2)

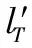
为了简化分析,在控制系统设计过程中忽略重力和马格努斯力,在式(1)的平衡点处做雅可比线性化处理,可以得到状态方程为

(3)

其中

输出方程为

(4)

其中

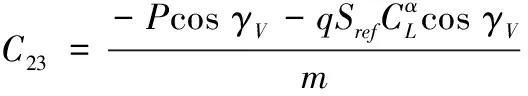
D11=cosγV,D12=sinγV

D21=sinγV,D22=-cosγV

选择状态变量、控制输入和量测输出分别如式(5)所示,可以得到线性化的火箭弹动力学模型为

(5)

在式(3)和式(4)中,由于在火箭弹飞行过程中,各参数依赖于飞行的平衡点,具有时变的特性,具体为

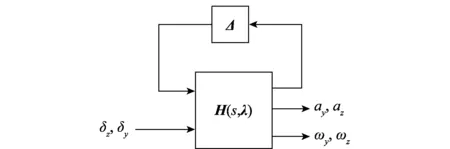
图1 火箭弹动力学模型的上LFT描述Fig.1 Upper-LFT description of the dynamics model of the rocket

图中

G=Fu(H,Δ)

(6)

Δ=

(7)

2 控制器设计

为了使加入控制器以后的闭环系统尽量具有期望的响应,并且对系统的参数摄动具有鲁棒性,采用H∞混合灵敏度设计方法。然而,传统的H∞混合灵敏度方法得到的控制器阶次通常比较高。文献[14]提出了具有固定结构的控制器,在已有的控制器结构框架下,通过H∞设计离线得到优化的控制参数,对于控制器本身没有更高的要求,可以兼顾实现难度和闭环系统的性能。

2.1 线性控制器设计

对于时变域中的任一点λ0∈Γλ,基于H∞的S/KS/T/M混合灵敏度设计方法的框图如图2所示。

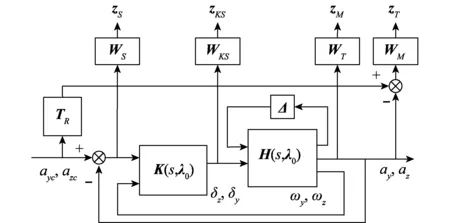
图2 综合混合灵敏度设计框图Fig.2 Mixed-sensitivity controller synthesis block diagram

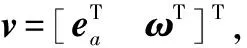
‖Twz(s)‖∞=‖Fl[P(s,λ0)K(s,λ0)]‖∞<γ,γ>0

(8)

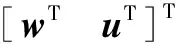
(9)

其中

传统的H∞控制方法所得到的控制器K(s,λ0)的阶次与增广系统的阶次一致,通常较高,而且在用于包含耦合的多变量控制时,容易造成保守性,并增加计算难度。对于火箭弹来说,希望控制器包含尽可能少的参数和微分,这样更易于控制器在嵌入式系统中的实现。自动驾驶仪控制器的设计目标是希望火箭弹加速度尽可能准确、迅速地跟随加速度指令,因此在误差控制部分应具有积分效应,其余控制部分取最简单的比例控制。

最简控制器的结构为

(10)

其中,Kroll-off(s)是滚降滤波器,选择为一阶惯性环节,带宽取执行机构带宽的一半，本文模型中未考虑执行机构动力学。其余控制器包含可调整参数,分别为

KS(s,λ0)=

考虑到俯仰、偏航方向动力学的对称性,需要优化参数,按照式(11)简化为6个。简化方式为

(11)

混合灵敏度的权值函数参照文献[12]中的选取方式。假设期望的参考模型形式为

(12)

其余的权值函数可以根据参考模型的参数来选择。

灵敏度的权值滤波器为

(13)

控制输入权值滤波器为

(14)

互补灵敏度函数的权值滤波器为

(15)

(16)

结构化H∞控制器综合是在附加控制器结构约束的条件下解决H∞综合问题[14-15]。对于有约束的控制器,通过李雅普诺夫方法可以列写双线性矩阵不等式(bilinear matrix inequality, BMI),然而这种方法属于非确定性多项式(non-deterministic polynomial, NP)困难问题,难以求解。文献[16]提出非光滑优化方法,通过广义梯度和束方法得到优化的控制器参数,并且对于高阶模型具有通用性。但是,通过该方法得到的控制器是局部最优的,为了使局部最优更接近于全局最优,应当选择多个不同的起始点开始优化,该方法目前已经集成在Matlab的Robust Control Toolbox中。

2.2 闭环系统稳定性

根据第2.1节的方法可以求得λ0处的控制器,其在参数摄动情况下的鲁棒稳定性可以通过结构奇异值进行分析。加控制器后,鲁棒稳定性(robust stability, RS)分析图如图3所示。

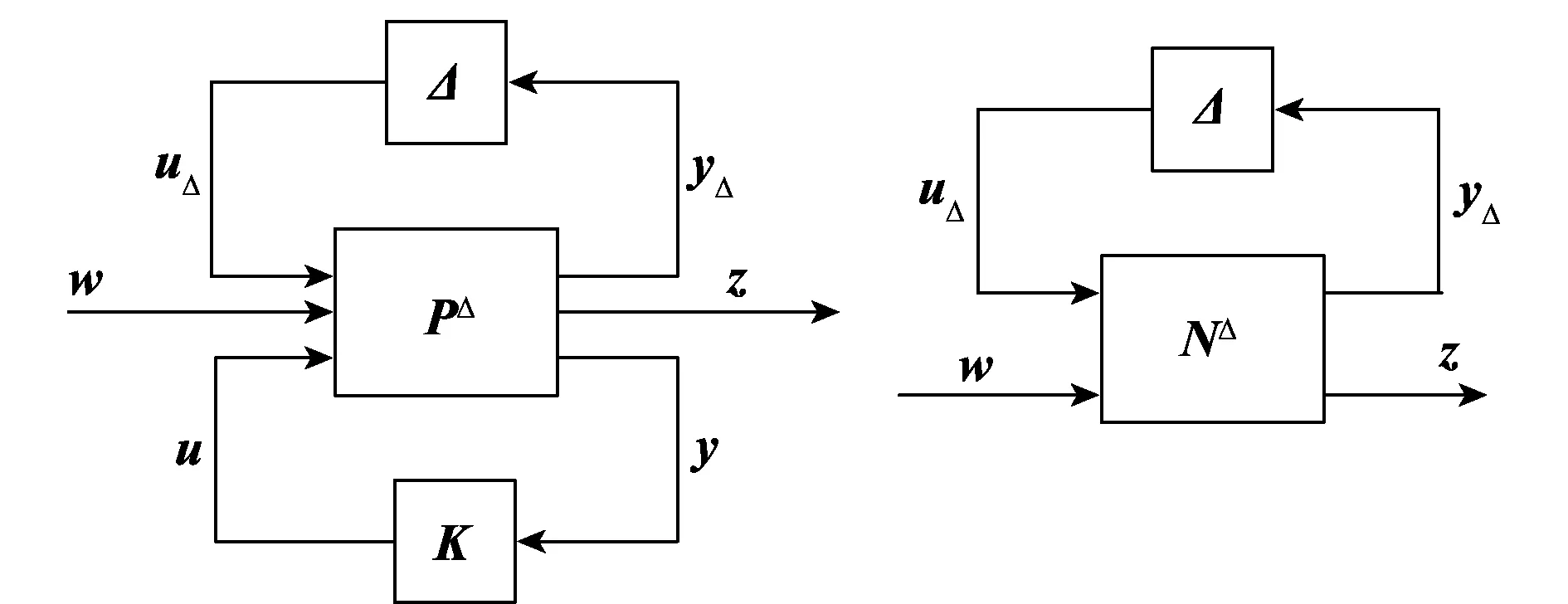
图3 鲁棒稳定性分析图Fig.3 Structure for robust stability analysis

其关系式为

(17)

式中,NΔ(s,λ0)=Fl[PΔ(s,λ0),K(s,λ0)]。

根据文献[17],系统在参数摄动条件下的RS条件可以表示为

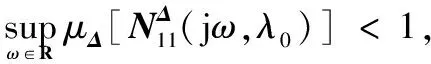
(18)

其中,结构奇异值μΔ(M)为在某一频率下使得矩阵I-MΔΔ奇异的具有最小结构的Δ的最大奇异值的倒数[17]，即

(19)

2.3 全局控制器

在参数空间内选择若干特征点,计算得到火箭弹的控制器参数,依照参数空间进行插值,即可得到全局控制器。特征点的选择需要尽量地覆盖所有可能出现的飞行状态,这样计算得到的控制器才能更好地适应各种飞行情况。具体的选择方式是:在续航段将速度和时间作为调度变量来设计控制器,在无动力飞行段,完全通过速度特征点来设计控制器。在计算完若干个孤立控制点后,根据当前的飞行状态使用插值的方式计算实时控制器参数,构造全局控制器。然而,对于全局闭环系统来说,由于系统是时变的,因此在所有特征点的局部稳定性并非是全局稳定性的充分条件。对于时变系统来说,其稳定性应当通过多次仿真来验证。

3 仿真

仿真分为3个部分:第1部分是设计某一特征点的控制器并分析特征点下的稳定性和性能;第2部分是设计全局控制器,分析局部稳定性;第3部分加入高度控制外环,分析不同指令下的全局稳定性。

本文使用122 mm火箭弹作为仿真模型。发动机为单室双推力,助推段工作约3 s,将火箭弹加速至约2.5个马赫数,续航发动机开始工作,其推力主要用于平衡阻力,使火箭弹在续航段维持大致稳定的速度。火箭弹在发射后5 s开始控制,续航发动机在发射后14.24 s结束工作。火箭弹的主要参数如表 1所示。

表1 火箭弹的主要参数

各气动数据不确定性根据气动数据表给出,推力不确定性取10 %,转速不确定性取10 %。下面以马赫数为2.5时的升力系数为例说明气动数据标称值和不确定性的计算方式。

升力系数在两条经过原点的直线范围内变化，如图4所示。

因此,升力系数对准攻角的导数，即图中直线的斜率为

(20)

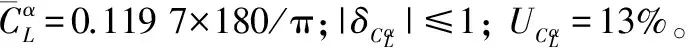
3.1 特征点下的控制器设计和稳定性分析

选择特征点λ0=[850,5]T,期望的带宽和阻尼分别为5 rad/s和0.8,在2%误差带条件下,使得期望的调节时间为0.75 s,按照第2节的方式设计控制器,对照选择为基于LMI设计的全阶控制器和对全阶控制器通过Hankel降阶至与式(10)相同阶次的控制器,使用3种控制器的闭环系统从扰动输入到性能输出的H∞范数如表2所示。

表2 3种控制器对比

3种控制器的性能对照如图5所示,对于灵敏度函数S(s),低频下小增益可以保证跟踪性能,中频时小峰值可以保证鲁棒性。从控制信号K(s)S(s)可以看出执行机构的余量。对于互补灵敏度函数T(s),低频时的单位增益可以保证跟踪性能,中频段小峰值可以保证对多种不确定性的鲁棒性和对噪声的低敏感性。对于模型匹配性能M(s),中频段的小值可以保证较好的模型匹配效果[18]。

图5 闭环系统性能目标和实际性能对比Fig.5 Closed-loop target and shaped performance

由图5可知,基于H∞设计的全阶控制器性能是最好的;具有固定结构的控制器较全阶控制器在性能上相差较小;基于Hankel奇异值降阶的控制器性能指标为无穷大,将直接导致闭环系统发散。考虑到控制器的工程可实现难易度与控制器阶次相关,而全阶控制器比固定结构的控制器高34阶,因此,在3种控制器中,具有固定结构的控制器最具优势。

通过SSV来分析闭环系统对于参数摄动的稳定性,用于分析鲁棒稳定裕度的结构奇异值上下界曲线，如图6所示。

由图6可知,SSV始终小于1。因此,闭环系统对于系统内摄动的参数具有鲁棒稳定性。

在参数摄动范围内随机取100个点,得到闭环系统阶跃响应曲线与参考模型阶跃响应曲线的对比，如图7所示。

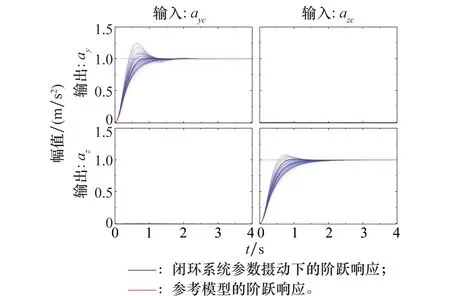
图7 闭环系统阶跃响应曲线Fig.7 Closed-loop step responses of the uncertain system

由图7可知,闭环系统基本上可以按照参照模型来跟踪输入指令。

3.2 全局控制器设计和稳定性分析

将续航段的特征点选择为按照0.3 s时间和25 m/s速度所划分的网格,时间和速度范围分别是5～14.24 s和800～925 m/s;将无动力飞行段的特征点选择为在525～900 m/s按照25 m/s所划分的节点。按照上述特征点选择方法,多次重复第3.1节的过程,得到增益调度控制器。各特征点处的最大结构奇异值如图8所示。

由图8可知,在各特征点处,闭环系统均是局部鲁棒稳定的。

在设计过程中引入不确定性的目的在于应对火箭弹飞行过程中各参数的时变性和非线性,从本节开始直接使用火箭弹6自由度非线性时变模型作为被控对象,仿真在9°发射高低角、0°发射方向角下进行,初始俯仰角速度为-0.1 rad/s,按照5 m/s2、幅值5 s、周期50%占空比的方波给出纵向、侧向加速度指令,两通道指令具有不同的相位,过载自动驾驶仪对方波指令的响应情况如图9所示。由于孤立特征点的性能并不能完整体现闭环全局系统的性能,因此在全局闭环系统中出现控制效果存在较大超调量的时刻。

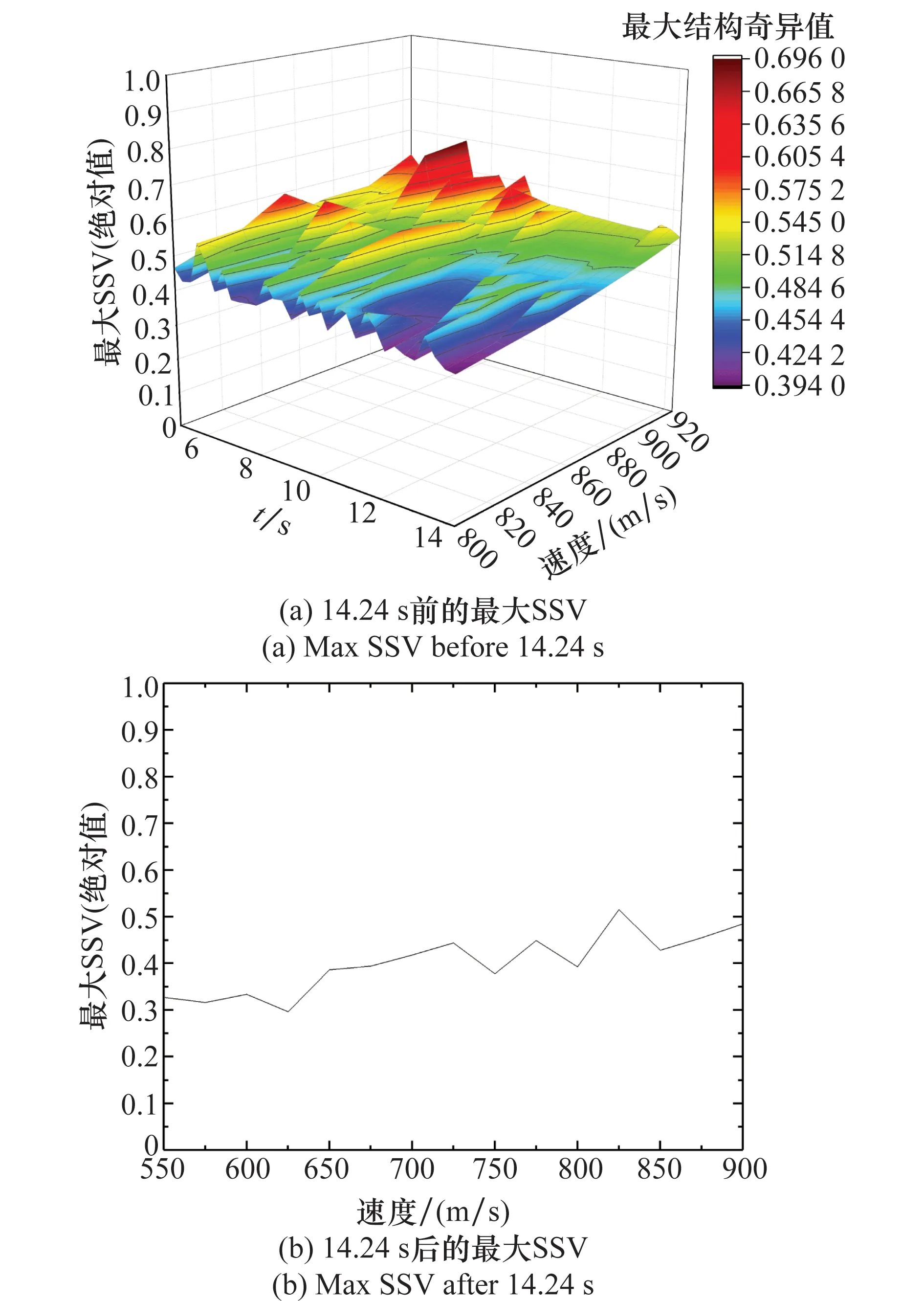
图8 各特征点的SSV最大值Fig.8 Maximum SSV values of the scheduling points

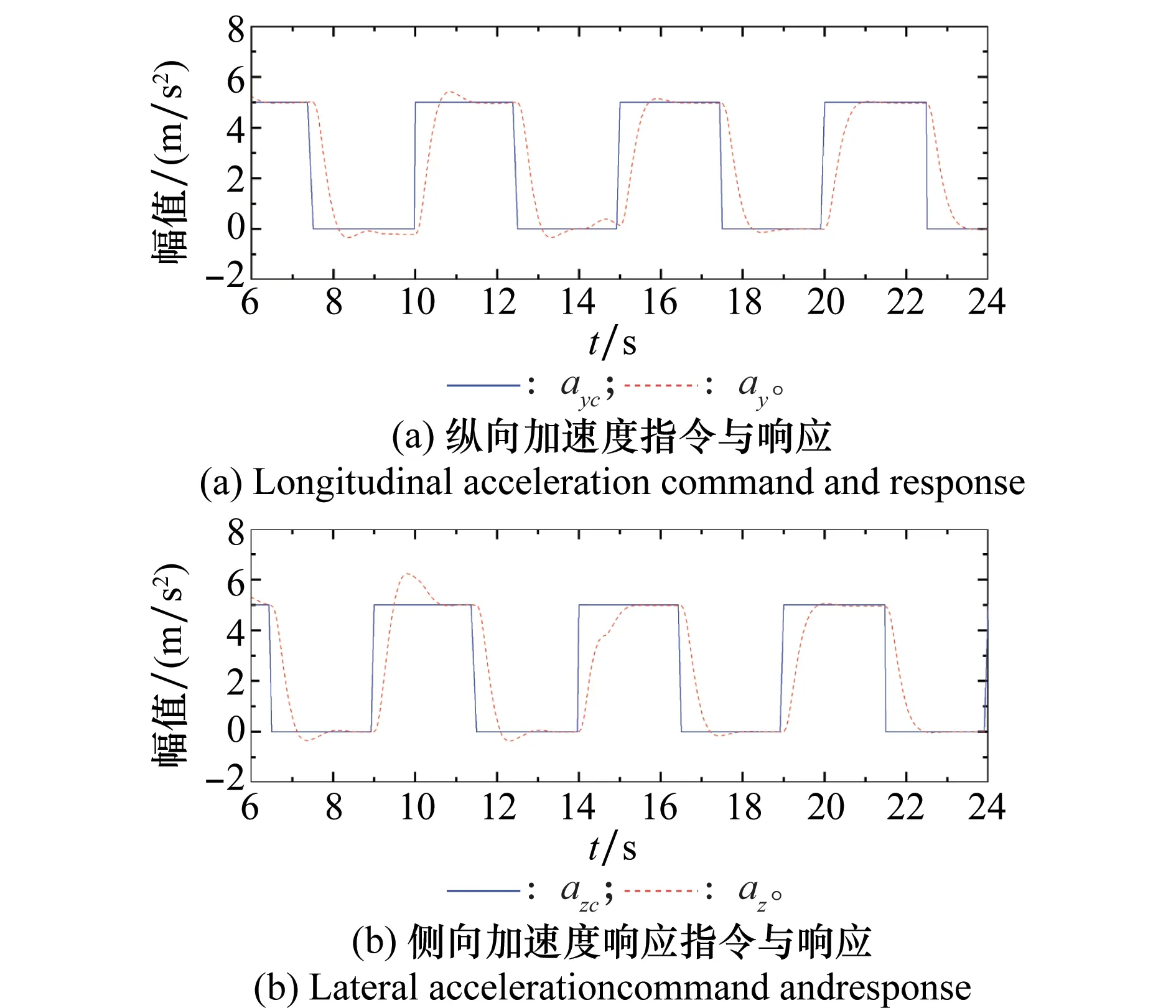
图9 闭环系统非线性仿真曲线Fig.9 Non-linear simulation of the closed-loop system

等效舵偏角曲线如图10所示。

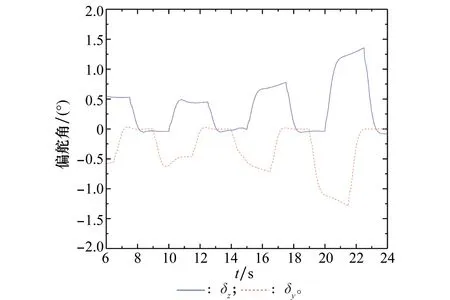
图10 仿真中等效舵偏角随时间变化曲线Fig.10 Equivalent canard deflection during the simulation

由图10可知,在推力消失后,速度下降导致提供同样过载所需的等效舵偏角增大。

3.3 平飞控制

火箭弹的设计目标是平飞控制,平飞高度100 m,参照文献[19]基于线性自抗扰控制(linear active disturbance rejection control, LADRC)分别设计纵向和侧向的位置控制器,以纵向为例,线性扩张状态观测器(linear extended state observer, LESO)带宽为6 rad/s,控制器带宽为1.3 rad/s,控制结构如图11所示。

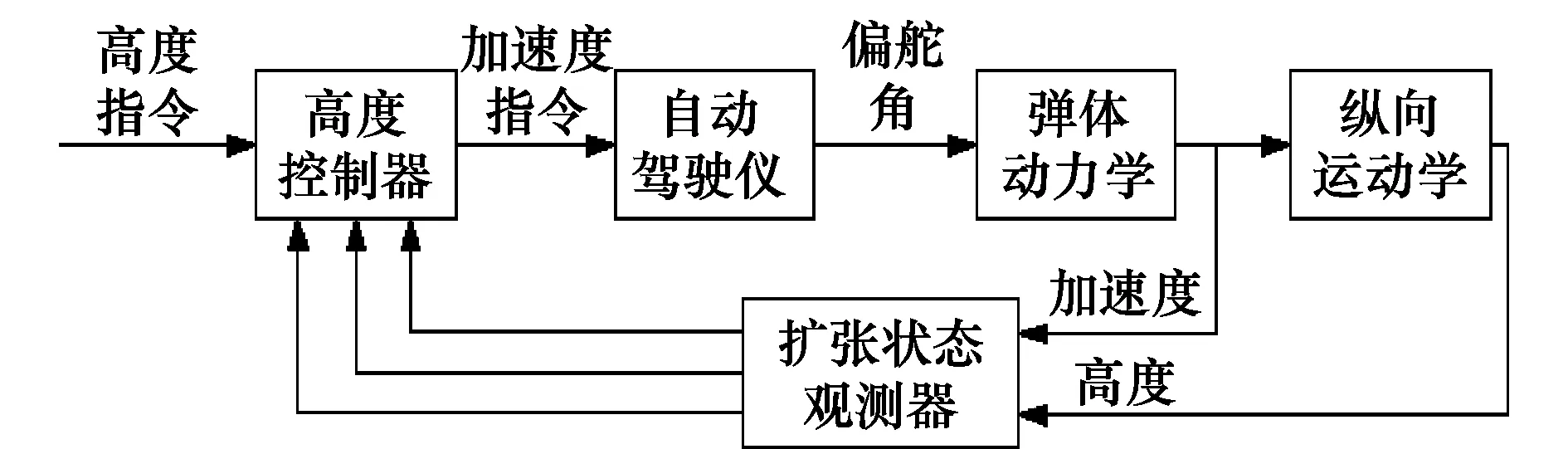
图11 高度控制框图Fig.11 Closed-loop height control system block diagram

在9°发射高低角,0°发射方向角的情况下,初始俯仰角速度为-0.1 rad/s,平飞控制结果如图12所示。

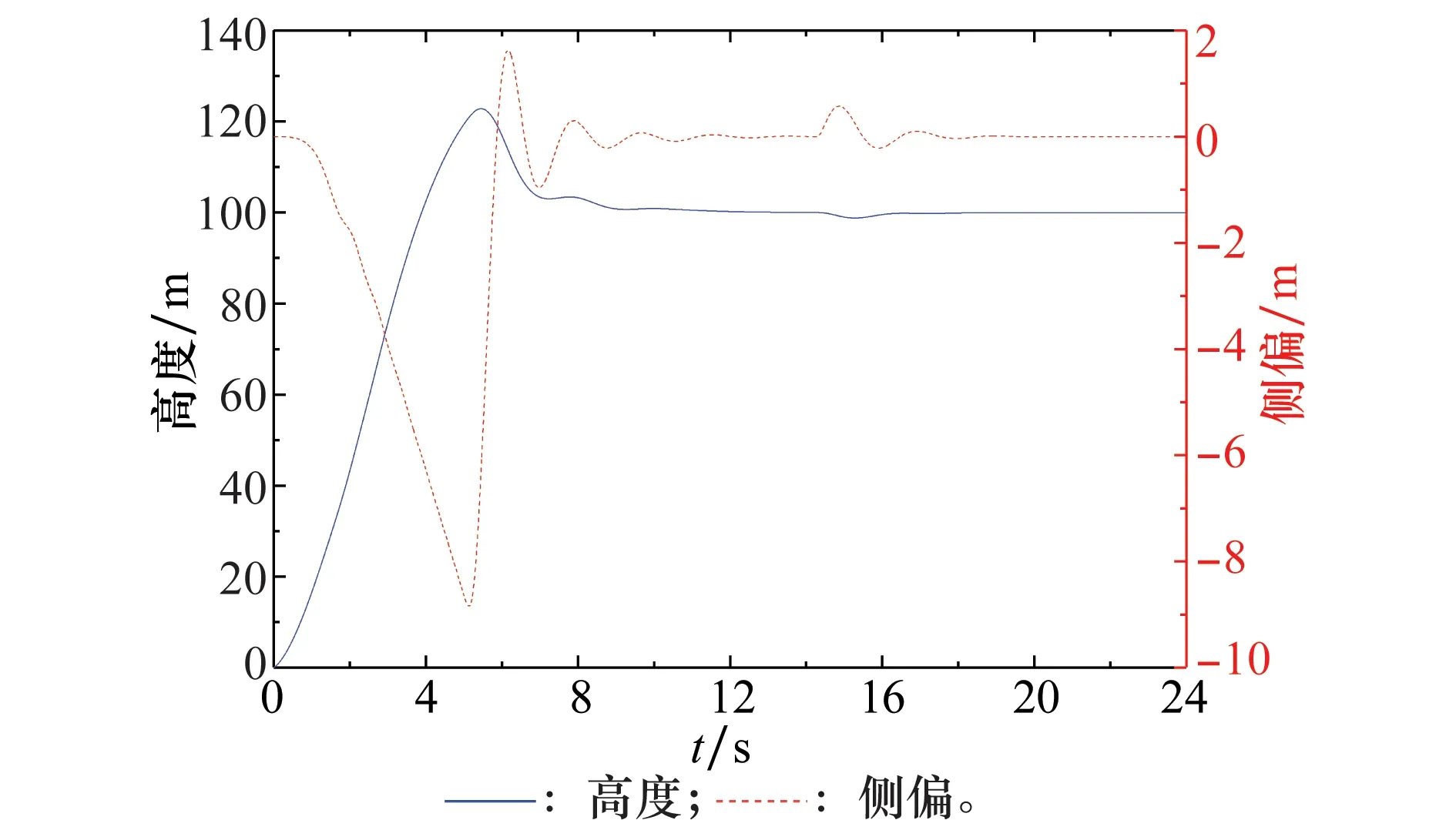
图12 高度和侧偏随时间变化曲线Fig.12 Height and offset vesus time

这种情况下，自动驾驶仪指令与响应曲线如图13所示。

若发射角高低角和偏角均有0.03°的误差,初始速度有2 m/s的扰动,空间弹道及其在侧向平面的投影如图14所示。

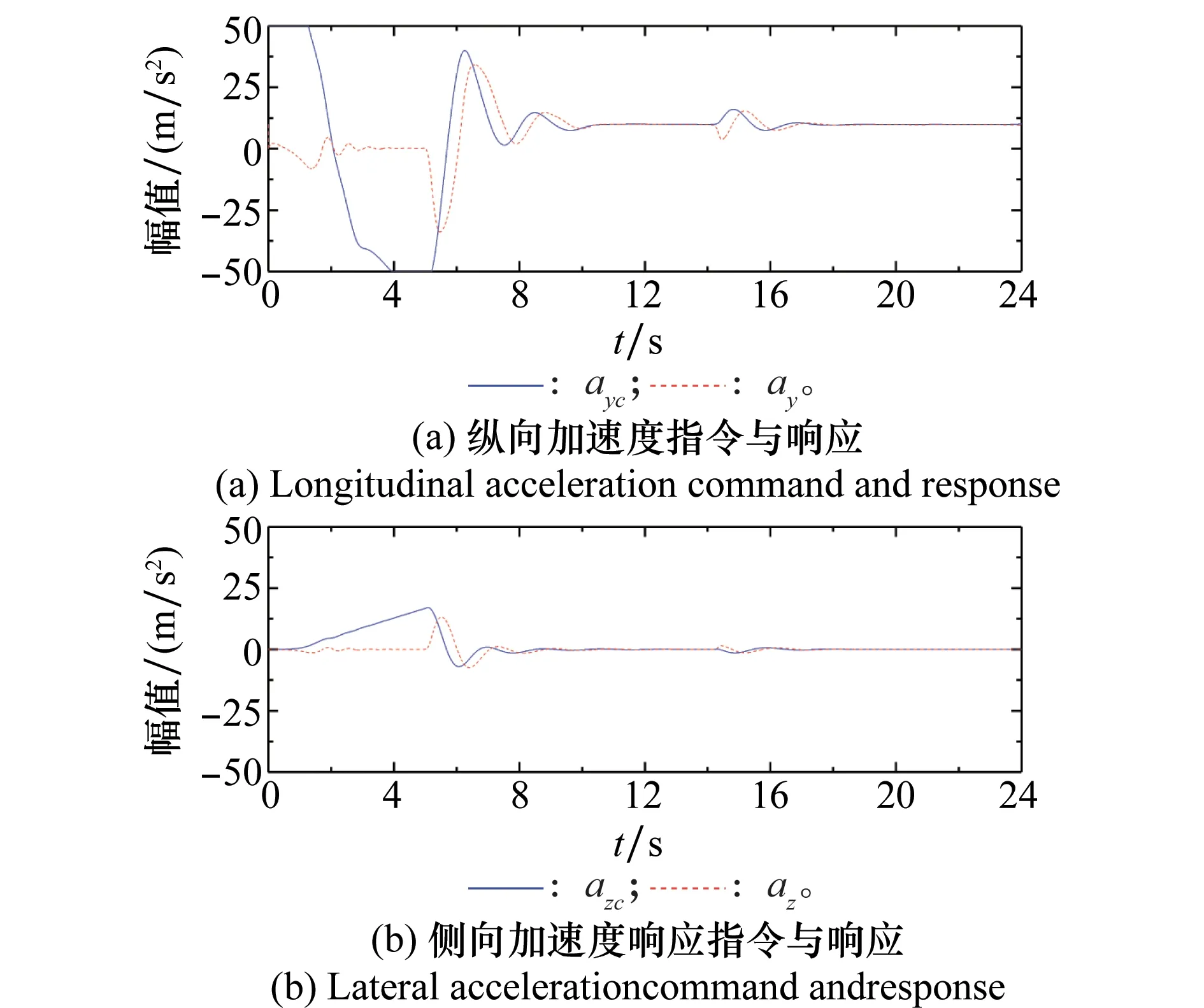
图13 自动驾驶仪指令与响应随时间变化曲线Fig.13 Command and response of the autopilot

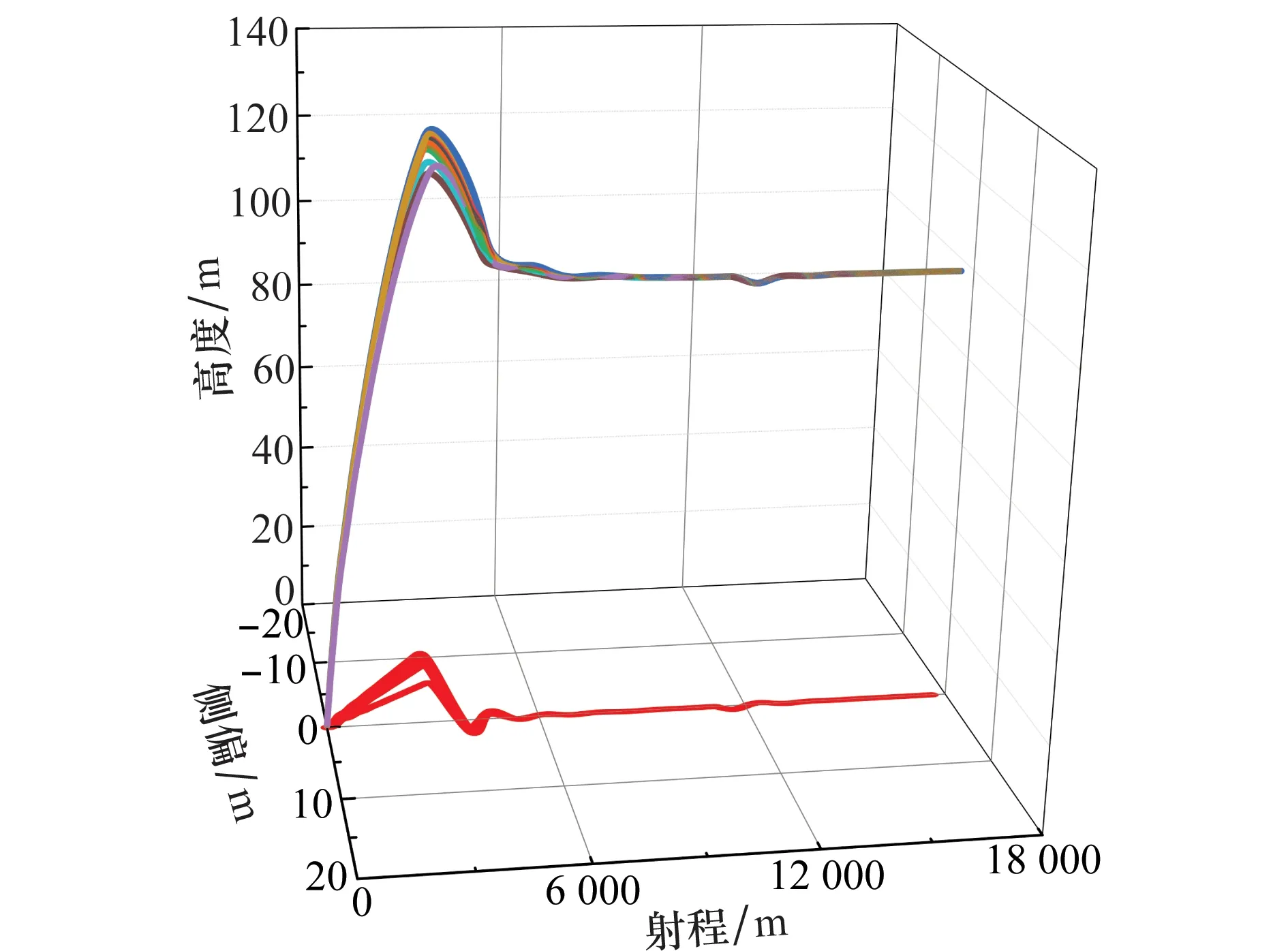
图14 扰动下的空间弹道曲线Fig.14 3-D trajectories under perturbation

由图14可知,闭环系统并没有出现不稳定的情况,说明在当前仿真条件下,闭环系统是全局稳定的。

4 结 论

基于雅可比线性化推导了火箭弹的俯仰、偏航动力学的线性化模型,使用鲁棒增益调度分别设计了针对火箭弹续航段和无动力飞行段的自动驾驶仪,设计中考虑了模型的时变特性和飞行状态中的参数不确定性。在续航段将速度、时间作为调度变量,在无动力飞行段将速度作为调度变量,将其他参数的摄动作为不确定性。通过SSV检验了各特征点下的闭环系统稳定性。仿真结果表明:通过本文方法设计的自动驾驶仪可以实现俯仰和偏航通道的解耦,同时能按照参考模型近似跟踪输入指令;附加较简单的位置控制回路可以实现定高平飞控制,对发射偏差具有鲁棒性。

[1] YANG S X, YAN X Y, XIONG F F. Trend of the artillery rocket and the problems related to control[C]∥Proc.of the 29th IEEE Chinese Control Conference, 2010: 6-13.

[2] 杨树兴, 张成, 朱伯立. 远程火箭弹简易控制方法[J]. 北京理工大学学报, 2004, 24(6):486-491.

YANG S X, ZHANG C, ZHU B L. Unsophisticated control method for long-range rockets[J]. Transactions of Beijing Institute of Technology(China), 2004, 24(6): 486-491.

[3] SIDDIQ M K, FANG J C, YU W B. SDRE based integrated roll, yaw and pitch controller design for 122 mm artillery rocket[J].Applied Mechanics and Materials, 2013, 415: 200-208.

[4] MOHAMMADLOO S, ALIZADEH M H, JAFARI M. Multivariable autopilot design for sounding rockets using intelligent eigenstructure assignment technique[J]. International Journal of Control, Automation, and Systems, 2014, 12(1): 208-219.

[5] FENILI A. Mathematical modeling and nonlinear attitude and trajectory tracking control of a one stage rocket with varying mass[C]∥Proc.of the 10th International Conference on Mathematical Problems in Engineering, Aerospace and Sciences, 2014: 321-330.

[6] 李伟明,白宏阳,辛明瑞,等.时敏制导炸弹离散自适应滑模BTT自动驾驶仪设计[J].系统工程与电子技术,2015,37(11): 2579-2585.

LI W M, BAI H Y, XIN M R, et al. BTT autopilot design for time-sensitive guided bombs based on adaptive discrete-time sliding mode control[J]. Systems Engineering and Electronics, 2015, 37(11): 2579-2585.

[7] MATTEI G, MONACO S. Nonlinear autopilot design for an asymmetric missile using robust backstepping control[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(5): 1462-1476.

[8] RUGH W J, SHAMMA J S. Research on gain scheduling[J]. Automatica, 2000, 36(10): 1401-1425.

[9] 于剑桥, 文仲辉, 梅跃松, 等. 战术导弹总体设计[M]. 北京:北京航空航天大学出版社,2010.

YU J Q, WEN Z H, MEI Y S, et al. Zhanshu daodan zongti sheji[M]. Beijing: Beihang University Press, 2010.

[10] ZHOU W, ZHAO L Y, LI K Y. Adaptive acceleration autopilot design for terminal guidance of a spinning rocket projectile[C]∥Advanced Materials Research, 2012:571-575.

[11] LEE H I, SUN B C, TAHK M J, et al. Control design of spinning rockets based on co-evolutionary optimization[J]. Control Engineering Practice, 2001, 9(2): 149-157.

[12] THEODOULIS S, SVE F, WERNERT P. Robust gain-scheduled autopilot design for spin-stabilized projectiles with a course-correction fuze[J].Aerospace Science and Technology,2015,42:477-489.

[13] 钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M].北京:北京理工大学出版社,2011.

QIAN X F, LIN R X, ZHAO Y N. Missile flight dynamics[M]. Beijing: Beijing Institute of Technology Press, 2011.

[14] APKARIAN P, NOLL D. NonsmoothH∞synthesis[J]. IEEE Trans.on Automatic Control, 2006, 51(1): 71-86.

[15] APKARIAN P, DAO M N, NOLL D. Parametric robust structured control design[J]. IEEE Trans.on Automatic Control, 2015, 60(7): 1857-1869.

[16] GAHINET P, APKARIAN P. StructuredH∞synthesis in Matlab[J]. IFAC Proceedings Volumes, 2011, 44(1): 1435-1440.

[17] ZHOU K M, DOYLE J C, GLOVER K. Robust and optimal control[M]. New Jersey: Prentice Hall, 1996.

[18] SKOGESTAD S, POSTLETHWAITE I. Multivariable feedback control: analysis and design[M]. New York: Wiley, 2007.

[19] GAO Z Q. Scaling and bandwidth parameterization based controller tuning[C]∥Proc.of the IEEE American Control Conference, 2003: 4989-4996.