基于遗传优化GRNN神经网络的人脸识别算法

简 毅，卢 峥，蒲永材，李坤贺

(中国兵器装备集团自动化研究所， 四川 绵阳 621000)

人脸识别技术已成为模式识别和计算机通信领域的热点，近年来得到了越来越多的应用。人脸识别率是评判人脸识别技术性能的指标之一。为了提高识别率，可采用人工神经网络技术完成人脸图像的识别[1]。人工神经网络迄今发展了几十年，在其持续发展过程中，诞生了诸多类型的神经网络[2]。先后有感知神经网络模型、自适应线性神经网络模型、BP(Back Propagation)神经网络模型[3]、RBF(Radical Basis Function)神经网络模型[4]、Hamming神经网络模型[5]以及GRNN(General Regression Neural Network)广义回归神经网络模型[6]和PNN(Probabilistic Neural Networks)神经网络模型[7]等多种神经网络类型。目前的研究以BP神经网络、PNN神经网络和GRNN神经网络居多[8-13]，其中GRNN神经网络在应用于人脸识别时的识别性能最佳。然而，由于不同平滑因子所对应的识别算法性能存在一定的差异性，使得GRNN神经网络应用于人脸识别时存在一定的局限性。因此，获得合理的平滑因子参数可以有效提升算法的仿真性能。

1 基于GRNN神经网络的人脸识别算法

1.1 人脸识别技术

人脸识别技术主要是基于人的面部特征，针对图像或者视频检测其是否存在人脸区域，若存在人脸区域，就进一步地检测出其位置、大小以及面部各个器官的位置等信息，根据上述信息可以得到每个人脸中的代表身份的特征，将上述特征与现有的人脸库进行比对，从而识别出人脸身份[14]，其具体流程如图1所示。

图1 人脸识别流程

首先，预处理人脸图像。由于采集到的人脸图像受到各种干扰因素的影响，比如光影，遮挡，采集角度。因此，需要处理干扰后的人脸特征数据。经过预处理后，可以得到较为高质量的样本特征数据。

其次，人脸特征提取。人脸的特征提取是主流人脸识别算法中必不可少的步骤之一，其提取方法的性能严重影响人脸识别算法的效率和准确率。其本质是得到人脸图像的特征数据。

最后，人脸识别。其本质是特征数据与现有的人脸库进行比对，识别出人脸身份。目前的研究常用神经网络来优化特征数据，从而提高人脸识别率。

1.2 GRNN神经网络

所谓神经网络,是一种模仿生物神经网络行为特征的分布式并行信息处理算法结构的动力学模型。将神经网络应用于人脸识别,一个直观的想法是建立一个神经网络,其中每个神经元对应图像中的一个像素[15]。目前存在很多关于基于神经网络的人脸识别的研究，其中GRNN神经网络识别性能最佳。

GRNN是一种基于非线性回归理论的人工神经网络模型，20世纪末由Donald F.Specht教授提出，其后，大量学者也在此网络的基础上进行的研究。GRNN广义回归神经网络对于处理各种应用中的问题有着优异的适应能力，且具有较为简便的训练和学习神经网络的步骤，因此在诸多学科和工业领域上得到了广泛应用。GRNN神经网络模型中解决的数学问题是非参数核回归，具体的步骤是用样本信息作为后验概率验证条件，对其进行非参数估计运算，再求解GRNN网络中因变量和自变量的关联密度函数，得到神经网络变量间的回归值，而关联密度函数的计算取决于神经网络中的训练样本。

假设GRNN神经网络中任意给定两个变量x和y，其条件均值可以表达为

(1)

式(1)中，f(x,y)是变量x和y的联合概率密度函数，X是对于给定变量x的观测样本。

通过对x和y的观测样本进行非参数估计，得到具体的概率密度函数，其表达式如下：

(2)

式(2)中，变量n和p分别表示样本数目和给定变量x的数据维数；变量Xi是对变量x进行观测后所得值，变量Yi是对变量y进行观测后所得值；变量δ表示神经网络中的光滑因数。

(3)

(4)

从上述公式中可知，GRNN神经网络在识别中性能的好坏很大程度上取决于其平滑因子δ，通过调节其数值能调整训练过程和结果输出的误差。

2 改进型遗传优化算法

本文基于遗传优化算法提出一种改进算法，对GRNN神经网络中的光滑因子进行最优化选取。

2.1 常用遗传算法

通常遗传优化算法的具体优化步骤如下：

步骤1：根据所需要处理的问题特点，对应于所求的问题解，选择一种编码，给出一个遗传算法的初始群体，使其包括M个染色体。

步骤2：求解对应于遗传算法中群体的所有染色体各自的适应函数值。

步骤3：在遗传算法的迭代过程中，当其结果符合所设定停止条件时，则算法停止迭代运算；如果不符合停止条件时，则继续用一个任给的概率值，抽出M个染色体组成新的遗传种群，再对新的种群进行迭代运算。

步骤4：对染色体进行交叉处理，让染色体中的优良遗传因子进行交换，最后得到M个染色体的交叉集合。

步骤5：设置一个合理的概率值对染色体中的部分遗传因子进行变异操作，变异后的新染色体组成新的遗传种群，再次计算种群中染色体的适应函数。

遗传算法的具体流程如图2所示。

2.2 改进型遗传优化算法

在实际应用中，普通的遗传算法，在较为复杂的图像识别领域中优化目标函数时，其优化结果不甚理想，有时出现优化速度缓慢，无法得到标准优化解的现象。针对这一现象，为了提高整体最优解参数的求解，解决运算时局部优化现象等问题，本文针对GRNN神经网络的特性从以下几个方面对遗传算法进行改进。

1) 遗传算子的实数编码

一般的遗传算法中，染色体中遗传因子的信息编码通常采用二进制数据编码，这种编码方式会导致空间搜索范围较小。为了解决这一问题，本文提出的算法使用实数编码方式进行遗传算法的遗传因子编码，采用该方式能使改进算法的速度和准确率得到提升。

2) 遗传算子中交叉概率和变异概率的自适应调节

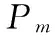
本文选用能够自适应调节的交叉概率和变异概率，确保群体的多样性，如下所示：

(5)

(6)

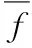
3) 交叉算子的改进

交叉算子的功能是遗传染色体中优良的遗传基因信息，通常的遗传算法在染色体进行编码的时候，使用二点交叉的方式。本文在实际进行染色体的实数编码时，使用算术交叉方式，具体表示为

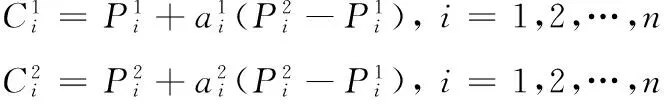
(7)

4) 变异算子的改进

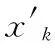
(8)

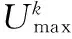
5) 混合选择算子的改进

本文采用3步混合选择操作：第1步，随机抽取m个染色体，并根据其适应度数值的大小进行排列，将这些染色体进行交叉以及变异操作；第2步，保留上一代染色体中的最佳个体；第3步，将m个子代进行交叉以及变异操作，然后按照第1步的抽取原则去除父代中遗传效果不佳的染色体。

混合选择算子的作用在保证算法运行效率的同时，可以防止算法陷入局部收敛，同时能较为合理地减少变异算子对染色体变异时的负面影响，对于维持算法中遗传种群的多样性起到重要作用。

3 基于遗传优化的GRNN神经网络的算法

根据上述改进遗传算法的原理，建立如下的优化目标函数：

Ffitness=GRNN(δ)

(9)

其中GRNN(*)表示GRNN神经网络的训练结果，光滑因子δ通过改进遗传算法进行最优搜索，其约束条件为0<δ≤0.1。其搜索结果如图3所示。

由图3可知，随着迭代次数的增加，GRNN神经网络的平滑因子不断趋于收敛，通过60次迭代之后，最后得到平滑因子的值为6.539 5e-04。因此，在最终的GRNN神经网络中，本文设置平滑因子为6.539 5e-04。

4 仿真结果与分析

为验证所提方法的有效性，本文针对两个标准人脸图像库：ORL人脸图像库和YALE人脸图像库对算法进行了性能测试，仿真对比本文所提出的人脸识别算法和几种典型的利用神经网络的人脸识别算法。仿真过程中人脸特征的提取采用HOG方向梯度直方图法。本文所提优化算法的主要仿真参数如表1所示。

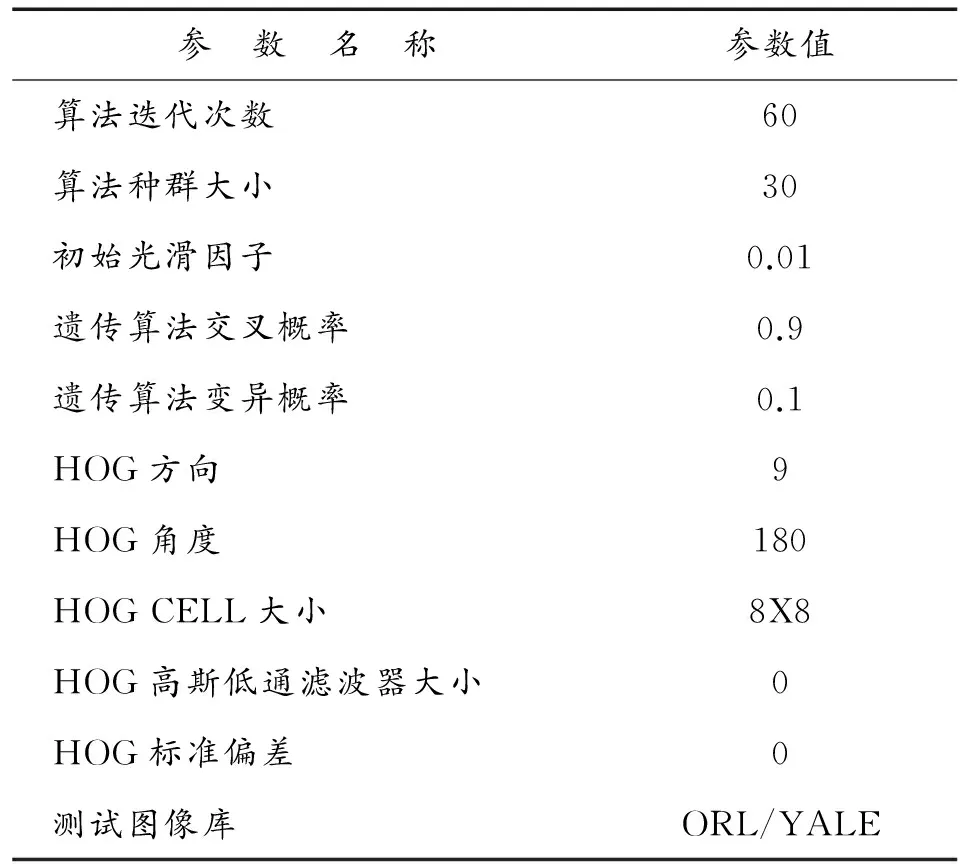
表1 本算法主要仿真参数

根据上述参数对GRNN神经网络进行ORL人脸图像库的人脸识别，并对比其他各算法的仿真结果如图4所示。

可见，当信噪比SNR大于0的时候，改进算法的识别率达到了88%左右，随着图像噪声的降低，系统的识别率稳定在88%左右，即改进算法的整体识别率在88%左右。

不同的算法的最大识别率如表2所示。

可知，改进后的GRNN神经网络相对于其余4种神经网络算法，识别性能有了进一步的提升，即改进后的GRNN神经网络，在保证原GRNN神经网络算法效率的前提下，进一步提升了识别性能。

算法仿真最大识别率/%BP73.95PNN77.17GRNN81.65DPNN85.89改进GRNN88.01

5 结论

因为GRNN神经网络中不同的平滑因子会产生不同性能的识别算法，所以获得合理的平滑因子参数可以有效提升算法的识别性能。本文针对该问题提出了基于遗传优化GRNN神经网络的人脸识别算法。该算法通过优化遗传算子选取光滑因子的最优值，并将光滑因子作为最优解求解参数，从而减小神经网络的识别误差。经仿真验证，在标准人脸图像库下，对算法施加干扰信息时，仍能达到88%以上的识别率，性能优于BP、PNN、GNN和DPNN神经网络识别算法。

：

[1] 冯建洋,谌海云.基于人工神经网络的人脸识别研究[J].自动化与仪器仪表,2017(5):24-26.

[2] AKERKAR R,SAJJA P S.Artificial neural network[C]//Intelligent Techniques for Data Science.Springer International Publishing,2016:125-155.

[3] LI J,CHENG J H,SHI J Y,et al.Brief introduction of back propagation (BP)[J].Neural Network Algorithm and Its Improvement,2012,169:553-558.

[4] YU H,REINER P D,XIE T,et al.An incremental design of radial basis function networks[J].IEEE Transactions on Neural Networks and Learning Systems,2014,25(10):1793-1803.

[5] LIPPMANN R.An introduction to computing with neural nets[J].IEEE Assp Magazine,1987,4(2):4-22.

[6] SPECHT D F.A general regression neural network[J].IEEE Transactions on Neural Networks,1991,2(6):568-576.

[7] SAVCHENKO A V.Probabilistic neural network with homogeneity testing in recognition of discrete patterns set[J].Neural Networks,2013,46(7):227-241.

[8] 邹莹莹,邓开发.基于小波PCA与BP神经网络的人脸识别算法[J].信息技术,2015(6):8-11.

[9] 张乾燕,梁量.Gabor滤波和蚁群优化BP神经网络的人脸识别[J].湖南科技大学学报(自然科学版),2012,27(4):69-72.

[10]SUN X Y,KANG F N,WANG M M,et al.Improved probabilistic neural network PNN and its application to defect recognition in rock bolts[J].International Journal of Machine Learning & Cybernetics,2016,7(5):909-919.

[11]段磊,马义德,许勇,韩明秋.一种改进的基于小波变换与PNN的指纹识别算[J].自动化技术与应用,2005,24(6):13-15.

[12]TRIPATHI M M,UPADHYAY K G,SINGH S N.Electricity price forecasting using generalized regression neural network (GRNN) for PJM electricity market[J].International Journal of Management-Theory and Applications (IREMAN),2014,2(4):137-142.

[13]BANERJEE P K,DATTA A K.Generalized regression neural network trained preprocessing of frequency domain correlation filter for improved face recognition and its optical implementation[J].Optics & Laser Technology,2013,45(8):217-227.

[14]徐晓艳.人脸识别技术综述[J].电子测试,2015(10):30-35.

[15]薛冰,郭晓松,蒲鹏程.人脸识别技术综述[J].四川兵工学报,2010,31(7):119-121.