盘–缝–带伞超声速充气过程仿真研究

王祁 曹义华



盘–缝–带伞超声速充气过程仿真研究

王祁 曹义华

（北京航空航天大学，北京 100083）

随着火星探测着陆研究的发展，对其主要的减速方式——盘–缝–带伞应用的研究也日趋火热。而在火星探测中，对伞衣充气过程的分析又是最为复杂的难题之一。文章介绍了常用于降落伞流场求解的数值模拟方法，并对它们的利弊做了简要的描述。文章使用守恒元/解元方法对盘–缝–带伞在超声速条件下，从收束状态开始的充气过程进行了数值模拟。首先对前置体进行单独仿真，之后在不同的马赫数下通过对降落伞系统的整体仿真完成对降落伞开伞过程的模拟。仿真数据与实验数据进行对比，获得了较为一致的结果，验证了方法的可行性。另外，文章对两种工作状态下的充气过程进行了对比，分析了盘–缝–带伞在两者中充气过程的异同，以及前置体阻力贡献随着马赫数的变化。最后通过开伞云图对充气过程中的开伞失败现象进行了分析。研究结果可为火星探测提供参考。

盘–缝–带伞 流固耦合 守恒元/解元方法 超声速 探测着陆

0 引言

在常见的火星探测器着陆减速系统中，盘–缝–带伞是典型的超声速、低密度降落伞伞型，在超声速、低密度的工作环境中稳定性好，充气性能优良。国外已成功着陆的Viking1、Viking2、MPF等火星探测器均采用了盘–缝–带伞[1-2]。降落伞的充气过程是整个工作过程中最复杂的一个阶段，充气过程处于一个快速的大变形状态，涉及到结构动力学与流体力学耦合的相关问题[3]，这些在文献[4-7]的试验结果中均有体现。而对于火星降落伞来说，低密度高马赫数的工作环境又很难通过试验完成，因此对这一领域进行仿真研究显得尤为重要[8-10]。

降落伞流场的数值模拟主要有两种方法。一种是涡元法。它在建立流场方程的基础上，通过伞衣型面及尾涡面上的边界条件，求解出绕伞衣流场的数值解。涡元法最大的好处是容易收敛，在轴对称伞衣上的计算结果非常好，但这种方法通常用在不可压流场的计算中。另一种是基于网格的流固耦合方法。常用的方法中，又可以分为传统的松散耦合方法（详见文献[11]，由于工作量大且精度无法保证，不建议采用）、任意拉格朗日欧拉（Arbitrary Lagrange Euler，ALE）方法和守恒元/解元（Conservation Element and Solution Element Method，CE/SE）方法。

ALE方法最初用于数值模拟流体力学的有限差分方法中，兼有Lagrage方法和Euler方法的特长，使得网格不至于出现严重的畸变[12]。国外的文献中无论是理论研究还是工程研究都已经频繁的使用过ALE方法[13-15]。这种方法在处理大变形问题时非常的有利，但是由于在超声速条件下，ALE方法计算耗时长，难收敛，往往得不到正确的结果，还可能出现计算终止，所以其更适用于计算亚声速[11,16]。

CE/SE方法，又称为守恒元/解元方法，是一种全新的守恒方程计算方法，国外文献对于这一方法的理论研究较为成熟[17-19]。它可以与浸润边界法[20]一起使用，将时间和空间统一起来同等对待，构造比较简单。除了简单的泰勒展开之外，CE/SE方法不需要采用其他的数值方法，尤其是不用通过其他的特征分析数值方法（如Riemann求解器）来捕捉激波、抑制振荡等[21]。

在研究降落伞领域，基于ALE方法的流固耦合数值仿真已经比较成熟，而CE/SE方法的工程化应用较晚，针对这一方法在降落伞领域的研究并不多。国内对于新方法的研究则还处于起步阶段，包括对降落伞充气过程的简化以及充气马赫数的选取都不能较为准确的反应盘–缝–带伞的真实充气过程。因此，对盘–缝–带伞超声速充气过程的仿真研究具有一定的理论意义和实践价值。

1 仿真过程

1.1 仿真模型

盘–缝–带伞是开缝伞的一种，如图1（a）所示，主要由伞衣、伞绳和吊带等组成。其中伞衣由平面圆形“盘”和圆筒型“带”组成，中间由缝隙将两者垂直分开。伞衣幅呈扇形，盘的中间有通气孔。在盘和带的周向径向均有加强条带，以防止伞衣过度张开[1]。图1（b）为伞衣的网格示意图。为了能够和文献[12]中的实验数据进行对比，本文选用了文献中相同的伞型。这是一种缩比的维京伞，相关的数据在表1中列出。

仿真模型中使用的前置体为具有70°钝角的减速体，整体采用结构网格进行划分。相关的数据体现在图2中，图中半径1=0.085m，2=0.852m。

如图3所示，选用圆柱形流场，这样既可以很好地捕捉伞衣的尾流，又可以减少流域边界对仿真结果的影响。由于降落伞带有前置体，所以流场的周向和径向都进行了加密。为了简化模型，外流域选用了相对稀疏的网格，但是相邻网格的体积增长控制在30%以内。CE/SE方法所使用的网格和ALE方法比较接近，均使用不兼容的网格，即流场和降落伞为两套互无搭接的网格。所不同的是CE/SE方法可以在初始运算中将气流静压带入到流场中，而ALE方法则需要外包一层提供流场静压网格，同时来流也需要单独设置，所以两者的流场不甚相同。本文中接触边界的力传递采用了浸润边界法，所以也不需要生成特殊的边界层网格。实际上在大变形情况下采用传统方法处理边界层更容易产生网格畸变。

表1 盘–缝–带伞模型参数

Tab.1 Disk–gap–band parachute model parameters

图2 前置体模型参数

图3 流场模型

1.2 流场仿真条件

流场的仿真条件来自于文献[12]，已整理在表2中。因为是火星的大气条件，所以密度要比地球低很多，这种低密度高马赫数的开伞条件也使仿真结果更加接近真实充气环境。

表2 流场仿真条件

Tab.2 Simulation Condition of fluid field

2 仿真结果的试验验证

由于降落伞的阻力是在不停的变化中，而且在高马赫数条件下降落伞充气过程中的阻力剧烈振荡，仿真的准确性很难通过阻力衡量。所以仿真分为两部分，首先针对没有伞衣作用的前置体进行仿真，通过仿真结果与实验数据的对比来验证仿真对阻力捕捉的准确性。在此基础上再对伞衣的充气过程进行仿真。由于马赫数=2.8时，缺少伞衣的试验数据，将选用=1.2，1.6，2.0，2.4作为数据验证。试验数据来源于文献[12]。如图4所示，在前置体的仿真结果中，实验数据和仿真结果拟合的非常接近，这说明CE/SE方法和浸润边界法在获取静态物体的阻力系数时是有效的，对边界层的处理也是符合物理实际的。

仿真结果显示，伞衣的阻力系数也和实验结果很接近，如图5所示。由于降落伞在仿真过程中未考虑伞衣透气性，所以阻力系数会在部分时刻大于实验值。

图4 前置体仿真结果与实验数据对比

图5 伞衣仿真结果与实验数据对比

需要说明的是，由于“呼吸”现象（伞衣第一次充满后，伞衣继续向外扩张充气，导致降落伞阻力面积峰值大于设计的全充满阻力面积，使开伞充气过程中最大开伞力预测精度降低[22]），伞衣的阻力是不稳定的，而耗费大量的时间求取伞衣稳定状态下的阻力系数也不是本文的研究重点，所以这里的阻力系数近似选取是伞衣第一次完全张满的状态，这里的结果仅作为仿真有效性的参考。

3 仿真结果分析

3.1 不同马赫数下的充气过程

由于模型的伞衣收束状态是完美的，所以盘–缝–带伞的充气会首先在顶盘处开始。呈锥形收束的伞盘通过充气膨胀，继而带动伞带扩张，因此在充气过程中伞带的投影面积始终小于伞盘。同时，通过仿真结果可以看出，降落伞在第一次充气之后，其投影面积会在一定范围内波动，这种“呼吸”现象在真实的试验过程中多次出现[22]，可见仿真结果比较真实的再现了降落伞的实际充气过程。盘–缝–带伞主要应用于超声速环境下，而且在=2.7以下性能是比较好的，在达到=2.7时会呈现较大的振动现象[23]。基于以上原因，在本小结中主要分析=1.2和=2.8两种速度下的充气过程，其中=1.2表征了降落伞的正常工作状态，=2.8表征了降落伞的非正常工作状态。图6所示即为盘–缝–带伞在=1.2条件下的充气过程。可以看出其在正常工作状态下可以很好的完成充气，其伞衣振荡幅度也比较小。

图7所示为=1.2条件下，盘–缝–带伞的开伞充气过程速度云图。在时间=0.004s，即充气的初始时刻，气流从伞衣下部入口进入，在伞衣内壁阻滞，使得伞衣开始变形。之后随着进入气体的增多，伞衣变形逐渐加大，在=0.3s高速气流到达顶孔并溢出。由于顶孔的阻滞作用，进入的气流大于顶孔流出气流，伞衣开始快速膨胀，多余的气体迅速充满伞衣内腔，开始从伞缝区域外流。最终进入的气体和流出的气体达到平衡状态，伞衣进入完全张满的稳定状态。

盘–缝–带伞在不同工作环境下的性能表现是不同的。由于其有能够正常工作的马赫数区间，故而在高马赫数条件下降落伞会发生剧烈的抖动。这些抖动对降落伞的影响是不确定的，降落伞有可能会最终给张开并稳定，但是也有可能因为剧烈抖动而发生开伞失败，如图8所示。根据仿真结果来看，=1.2时，降落伞开伞成功，形状和阻力最终都趋于稳定，而=2.8时则会发生剧烈振荡，最终导致降落伞的开伞失败。

3.2 不同马赫数下的阻力变化过程

阻力变化和降落伞的充气过程是紧密联系的，降落伞过度扩张的时间点也恰好是阻力值达到最大的时刻。同时，=2.8条件下的阻力变化要远远剧烈于=1.2，可见马赫数对降落伞的充气表现至关重要。同样的伞型在不同的马赫数下也会有不同的阻力表现。

图9所示为=1.2条件下的阻力变化过程。可以明显的看出，虽然阻力在很小的范围内振荡，但是整体是较为平滑的。虽然在图中看不出比较明显的稳定迹象，但是根据开伞过程动画可以看出，降落伞在=1s时已经趋于稳定。

图10为=2.8条件下的降落伞阻力变化曲线。通过和=1.2的仿真结果对比可以看出，在相同时间内阻力发生了更为剧烈的振荡，而且在阻力的变化过程也是极其的不稳定。这样的结果也可以在开伞动画中得到体现，伞衣的张开过程很不稳定，会出现剧烈的抖动。这些抖动使伞衣的形状变化不再具有规律，过度的扩张导致过度的收缩，进而影响结构透气性，导致最终的开伞失败。

图9 Ma=1.2时，伞衣阻力变化过程

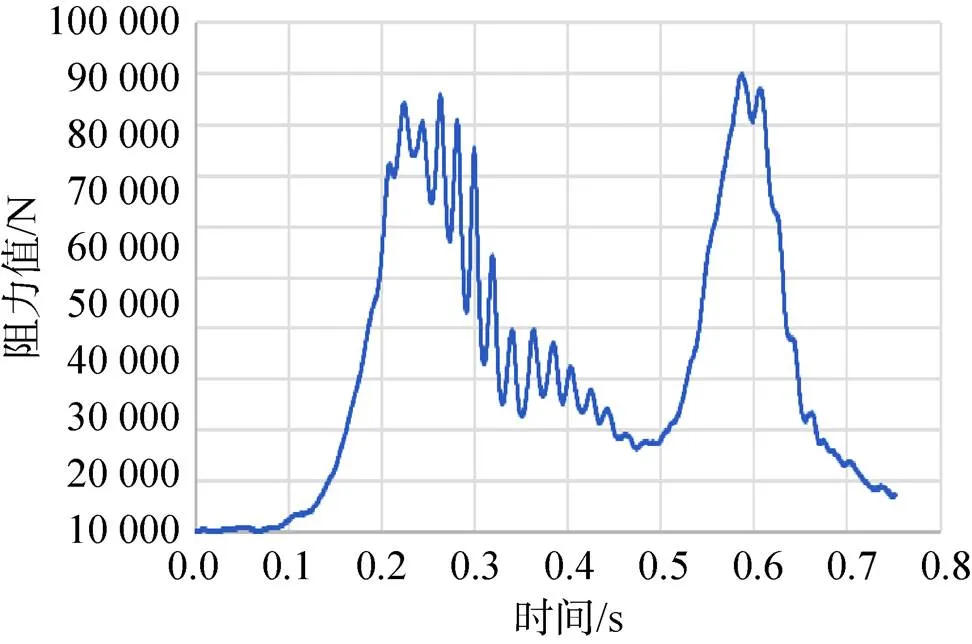
图10 Ma=2.8时，伞衣阻力变化过程

3.3 充气过程中前置体阻力贡献

图11所示为=2.8时，降落伞充气过程中的流场云图。可以看出前置体处对气流的影响范围要比伞衣大一些，但是对气流的减速效果远小于伞衣，激波范围也小于伞衣。同时，图中可以看出前置体的存在会对流经伞衣的气流有减速效果，但是减速效果有限。

图12所示为=2.8条件下前置体阻力的求解过程，从图中可以发现，对于固定的物体来说求解是十分稳定和迅速的。通过将前置体的阻力占伞衣张满状态下的整体阻力的百分比求出即可得到前置体在降落伞整体减速效果中的贡献量。可以看出，随着马赫数的增长，前置体所占百分比逐渐增多，如表3所示。由于这里的阻力为降落伞完全张满的阻力，所以在充气过程中前置体的减速效果更加巨大，这一部分的初始减速直接决定了伞衣的开伞和张满状态的工作马赫数。

图11 Ma=2.8时，降落伞整体速度云图

图12 Ma=2.8时，前置体阻力变化曲线

表3 前置体阻力贡献比率

Tab.3 Contribution ratio of the probe drag

3.4 开伞失败的过程分析

通过对比=1.2（在3.1节中已通过图7进行过分析）和=2.8下开伞过程云图的异同，可以得出为什么高马赫数下降落伞更容易开伞失败。在=2.8时，从图10中可以看出，降落伞前后共经历两次阻力峰值，分别在=0.243s左右与=0.584s左右。在=0.243s后降落伞经历多次“呼吸”现象，但整体是收缩状态，在=0.5s时刻恢复扩张状态。而在=584s之后则经历急速收缩，直到充气失败。

图13所示即为=2.8时，=0.243s前后降落伞一次“呼吸”现象的速度云图，其中色温越高表明气流的速度越大。可以明显看出，在=0.199s时，降落伞内部气流是正常的充气状态，而=0.224s时开始伞衣内部回流气体增多，此时降落伞开始扩张。但是回流的气体并不能稳定的维持在伞衣内部，而是在伞衣内部呈现不规则的变化。

图14为与图13同一时刻的密度云图。综合图13和图14，可以看出，在=0.224s时降落伞内部的高压区扩大，由于内部气体受压，不能及时从顶孔排出而产生阻滞，阻滞的气流逐渐增多影响了激波的形状，激波影响域加大，使得进入降落伞的气流减少，内部气压降低，在弹性伞衣的回复力作用下，=0.224s之后伞衣开始塌缩。而在=0.264s和=0.299s之间，阻滞在伞衣边缘的回流气体将整体的正激波挤压分流，给了外部气流流入的机会，在=0.329时刻伞衣已经逐渐恢复扩张状态。

而在图15中，=0.579s附近，降落伞首先经历了和图13中一样的过度扩张，然而之后伞衣收缩严重，最终没有能够使伞衣重新张开。从图14中可以看出，伞衣的扩张依靠的是内部的阻滞气体。我们知道，气体的阻滞是因为伞衣吸收了来流的动量，转化为了阻力；阻滞气体量表征了降落伞伞衣吸收动量的能力。所有降落伞扩张的过程中，阻滞气体都布满了伞衣内壁；在图13中=0.329s时刻就存在这种现象，这也就是伞衣在=0.329s之后仍然可以恢复扩张的原因。而在图15中=0.689s，可以明显的看出，阻滞气体已经不占有优势。这说明此时伞衣并没有将来流的动量有效转化为阻力。在=0.744s，被分离的激波重新合为一个，但激波形状已经改变，无法正常工作了。顶孔此时已经偏离中轴线，所以在云图中无法看到，实际上顶孔仍然在剧烈的喷涌气体。综合来看，应该是过度扩张导致的恢复力大于了阻力，致使收缩过度，气体进入量减少，最终导致了开伞的失败。

通过=1.2和=2.8时充气过程的云图对比，可以看出，成功充气的盘–缝–带伞内部的低速气体是稳定的，同时速度也是一致的。而在高马赫数时由于进气量大于出气量，内部气流不稳定，容易导致激波的破裂，对气流的减速效果下降，伞衣整体的阻力也随之下降。气流的不稳定还会使伞衣形状发生剧烈变化，外型的改变是不可控的，伞衣在之后是否能回归正常充气则成了随机事件。尤其对于盘–缝–带伞来说，伞盘和伞带是由伞绳连接的，这就更加加剧了伞衣的变形幅度，伞带的坍缩会导致严重的后果。可见，对于工作于不同马赫数下的盘–缝–带伞，透气性的设计至关重要。

4 结束语

本文通过CE/SE方法对盘–缝–带伞在低密度超声速条件下的充气过程进行了仿真。通过对仿真结果的分析得出了以下结论：

1）CE/SE方法在对超声速流场的仿真求解过程中对计算资源的占用较小，耗时短，且与试验结果比较接近，是比较适合工程应用的新方法。

2）盘–缝–带伞可以在超声速条件下完成充气的过程，但是对马赫数有要求。在较高的马赫数条件下有开伞失败的风险。

3）前置体在盘–缝–带伞的充气过程中对伞衣的流场有一定影响，且会提供可观的阻力贡献。

4）伞衣内部的气体稳定性对盘–缝–带伞的整体稳定性有重要影响。伞衣内部气流的不稳定会使伞衣振荡剧烈，可导致开伞失败的严重后果。为了消解这一不利影响，盘–缝–带伞的结构透气性要谨慎选取。

[1] 高树义, 戈嗣诚, 梁艳. 火星盘–缝–带伞跨声速风洞试验研究[J]. 中国空间科学技术, 2015(4): 69-75. GAO Shuyi, GE Sicheng, LIANG Yan. Research on Transonic Wing Tunnel Tests of Mars Disk-gap-band Parachutes[J]. Chinese Space Science and Technology, 2015(4): 69-75. (in Chinese)

[2] 于莹潇, 田佳林. 火星探测器降落伞系统综述[J]. 航天返回与遥感, 2007, 28(4): 12-16. YU Yingxiao, TIAN Jialin. Mars Explorer’s Parachute System Overview[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(4): 12-16. (in Chinese)

[3] 荣伟, 鲁媛媛, 包进进, 等. 火星探测器减速着陆过程中若干问题的研究[J]. 南京航空航天大学学报, 2016, 48(4): 445-453. RONG Wei, LU Yuanyuan, BAO Jinjin, et al. Several Problems Relative with Descent and Landing Process of Mars Explorer[J]. Nanjing University of Aeronautics and Astronautics, 2016, 48(4): 445-453. (in Chinese)

[4] REICHENAU D E A. Aerodynamic Characteristics of Disk-gap-band Parachutes in the Wake of Viking Entry Forebodies at Mach Numbers from 0.2 to 2.6[R]. Arnold Engineering Development Center Arnold AFB TN, AEDC-TR-72-78, 1972.

[5] CRUZ J R, MINECK R E, KELLER D F, et al. Wind Tunnel Testing of Various Disk-gap-band Parachutes[C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Monterey, California, AIAA 2003-2129, 2003: 1-16.

[6] LINGARD J, BARNARD S, KEARNEY P. Comparative Study of the Performance of Parachutes at Mach 0.5 to Mach 4.35 with Reference to Suitability for Use with the Hermes Crew Escape capsule[C]//10th Aerodynamic Decelerator Systems Technology Conference, Cocoa Beach, AIAA 1989-889, 1989: 1-11.

[7] WITKOWSKI A, KANDIS M, ADAMS D. Inflation Characteristics of the MSL Disk Gap Band Parachute[C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar
, Seattle, Washington, AIAA 2009-2915, 2009: 1-9.

[8] BENDURA R J, COLTRANE L C, HUCKINS, et al. Performance of a 19.7 Meter Diameter Disk Gap Band Parachute in A Simulated Martian Environment[C]//National Aeronautics and Space Administration, Washington, D. C., 1968: 1-36.

[9] GAO X, ZHANG Q, TANG Q. Numerical Modelling of Mars Supersonic Disk-gap-band Parachute Inflation[J]. Advances in Space Research, 2016, 57(11): 2259-2272.

[10] TAYLOR A. An Investigation of the Apparent Mass of Parachutes under Post Inflation Dynamic Loading through the Use of Fluid Structure Interaction Simulations[C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Monterey, California, AIAA 2003-2014, 2003: 1-9.

[11] 杨璐瑜, 张红英, 陆伟伟, 等. 盘–缝–带伞超声速开伞过程研究[J]. 航天返回与遥感, 2016, 37(3): 29-38. YANG Luyu, ZHANG Hongying, LU Weiwei, et al. Study on the Deployment of Disk-gap-band Parachute in Supersonic Flow[J]. Spacecraft Recovery and Remote Sensing, 2016, 37(3): 29-38. (in Chinese)

[12] 王中阳. 降落伞充气过程动力学数值模拟[D]. 南京: 南京航空航天大学, 2013. WANG Zhongyang. The Dynamic Numerical Simulation of the Parachute Inflation[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013. (in Chinese)

[13] LINGARD J, DARLEY M, UNDERWOOD J C. Simulation of Mars Supersonic Parachute Performance and Dynamics[C]//19th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Williamsburg, VA, AIAA 2007-2507, 2007: 1-11.

[14] LINGARD J, DARLEY M. Simulation of Parachute Fluid Structure Interaction in Supersonic Flow[C]//18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Munich Germany, AIAA 2005-1607, 2005: 1-9.

[15] SOULI M, OUAHSINE A, LEWIN L. ALE Formulation for Fluid–structure Interaction Problems[J]. Computer Methods in Applied Mechanics & Engineering, 2000, 190(5): 659-675.

[16] 杨璐瑜, 陆伟伟, 张红英, 等. 速度对火星用盘–缝–带伞超声速开伞性能影响[J]. 航空计算技术, 2016, 46(5): 34-37. YANG Luyu, LU Weiwei, ZHANG Hongying, et al. Effect of Velocity on Performance of Mars Disk-gap-gand Parachutes in Supersonic Flow[J]. Aeronautical Computing Technique, 2016, 46(5): 34-37. (in Chinese)

[17] ZHANG Zengchan, JOHN Y S T. A Generalized Space-time CE/SE Method for the Euler Equations on Quadrilateral and Hexagonal Meshes[C]//15th AIAA Computational Fluid Dynamics Conference, Anaheim, CA, AIAA 2001-2592, 2001: 1-11.

[18] COOK G, ZHANG Z C, IM K. Applications of the CE/SE Method in LS-DYNA[C]//Applications of the CE/SE Method in LS-DYNA, San Diego, CA, AIAA 2013-3070, 2013: 1-10.

[19] TEZDUYAR T E, SATHE S, STEIN K. Solution Techniques for the Fully Discretized Equations in Computation of Fluid–structure Interactions with the Space–time Formulations[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(41): 5743-5753.

[20] MITTAL R, IACCARINO G. Immersed Boundary Methods[J]. Annual Review of Fluid Mechanics, 2005, 37(37): 239-261.

[21] 刘凯欣, 王景焘, 王刚, 等. 时–空守恒元解元(CE/SE)方法综述[J]. 力学进展, 2011, 41(4): 447-461. LIU Kaixin, WANG Jingtao, WANG Gang, et al. A Review on the CE/SE Method[J]. Advances in Mechanics, 2011, 41(4): 447-461. (in Chinese)

[22] 郭叔伟, 王海涛, 董杨彪, 等. 降落伞“呼吸”现象研究[J]. 航天返回与遥感, 2010, 31(1): 18-23. GUO Shuwei, WANG Haitao, DONG Yangbiao, et al. Research on Parachute BREATH Behavior[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(1): 18-23. (in Chinese)

[23] 韩晋阳, 徐宏, 高峰. 超声速半流伞设计与分析[J]. 航天返回与遥感, 2013, 34(5): 20-28. HAN Jinyang, XU Hong, GAO Feng. Design and Analysis of Supersonic Half-flow Parachute[J]. Spacecraft Recovery & Remote Sensing, 2013, 34(5): 20-28. (in Chinese)

（编辑：陈艳霞）

Study on the Simulation of the Inflating Process of Disk-gap-band Parachute in Supersonic Flow

WANG Qi CAO Yihua

（Beihang University, Beijing 100083, China）

With the development of Mars exploration and landing, the research on the decelerator, the disk-gap-band parachute, is becoming more and more popular, and the analysis of the inflation process is one of the most complicated problems. In this paper, the numerical simulation methods used to solve the flow field of parachute are introduced, and their advantages and disadvantages are briefly described. This paper use conservation element and solution element (CE/SE) method to simulate the inflation process of the parachute from folding state in supersonic speed. Firstly, the probe is simulated separately, then the inflating process of the whole system is simulated under different Mach numbers. The simulation result are compared with the experimental data, and the comparison results are consistent, which verified the feasibility of the method. In this paper, the inflating process under two working conditions is compared, and the similarities and differences are analyzed. The resistance contribution of the probe changing along with the Mach number is also analyzed. Finally, the phenomenon of failure in the inflation process was analyzed by the contours of the parachute. The research result can provide reference for Mars exploration.

disk-gap-band parachute; fluid-structure interaction (FSI); CE/SE method; supersonic; probe landing

V445.2+3

A

1009-8518(2018)01-0035-10

10.3969/j.issn.1009-8518.2018.01.005

王祁，男，1992年生。2015年获北京航空航天大学飞行器设计专业学士学位。现为北京航空航天大学航空工程专业硕士研究生。研究方向为降落伞回收系统流固耦合数值模拟。E-mail: shuimohaichen@163.com。

曹义华，男，1962年生。1990年获南京航空航天大学飞行器设计专业空气动力学博士学位，1992年南京理工大学气体动力学博士后出站。教授，研究方向为计算流体力学研究和飞行器设计。E-mail: yihuacaobu@126.com。

2017-08-22