降落伞强度空投试验模型的气动–动力学特性仿真

张章 王立武 王文强 王奇 吕智慧 李健



降落伞强度空投试验模型的气动–动力学特性仿真

张章1,2,3王立武1王文强1王奇1吕智慧1李健1

（1 北京空间机电研究所，北京 100094）（2 中国空间技术研究院航天器无损着陆技术核心专业实验室，北京 100094）（3 北京市航空智能遥感装备工程技术研究中心，北京 100094）

降落伞强度空投试验模型的气动-动力学特性仿真研究对空投试验方案设计和降落伞减速系统性能的考核至关重要。文章运用数值模拟手段分析了空投试验模型的气动特性和气动稳定性，探讨了降落伞开伞前空投试验模型的弹道轨迹和运动姿态的变化，并针对不同飞行攻角下空速管动压测试值与实际开伞动压存在相对偏差所造成的影响进行了分析。结果表明：空投试验模型的轴向力系数在攻角大于4°时有所下降。法向力系数和俯仰力矩系数随着飞行攻角增加以近似线性的方式增大，压心位置后移，气动稳定性良好。在模型投放后至降落伞开伞前的过程中，随着高度下降空投试验模型的速度以近似线性的形式增大，且俯仰角和攻角均存在周期摆动现象。由于飞行攻角的影响，空速管测得的动压值与开伞实际动压存在相对偏差，但相对偏差范围不会超过14%。研究结果可以为降落伞强度空投试验的方案设计提供参考。

降落伞空投试验 气动性能 动力学特性 动压偏差 数值模拟 航天返回

0 引言

大型降落伞广泛用于卫星[1]、飞船[2]、探测器等[3-4]航天器的气动减速与回收着陆。降落伞的性能关系到航天器回收着陆任务的成败[5]，它主要通过风洞试验[6-7]和空投试验[8]进行考核。

降落伞风洞试验属于约束试验方法，适用于无限质量条件下降落伞气动性能及开伞充气性能的验证[9-10]。降落伞空投试验属于非约束自由飞行试验方法，能够反映有限质量条件下降落伞的真实工作性能[11-12]。降落伞强度空投试验的主要目的是采用空投试验手段来验证降落伞强度性能，是航天器回收系统可靠性的关键试验验证环节。在降落伞强度空投试验实施之前，需要对空投试验模型进行气动性能仿真与动力学特性仿真，为降落伞强度空投试验的方案设计提供依据[13-15]。

本文对降落伞强度空投试验模型开展了气动仿真和动力学仿真，分析了空投试验模型的阻力特性和气动稳定性，探讨了降落伞开伞前空投试验模型的弹道轨迹和运动姿态的变化，并针对不同飞行攻角下空速管动压测试值与实际开伞动压存在相对偏差所造成的影响进行了分析。研究结果可以为降落伞强度空投试验的方案设计提供参考。

1 数值方法

仿真计算所涉及的数值方法可以分为气动仿真和动力学仿真两类。

1.1 气动仿真

本文采用CFD数值模拟的手段获取降落伞强度空投模型的气动性能。CFD流场计算的基本控制方程为雷诺平均N-S方程（RANS），湍流模型采用Menter SST模型，空间离散采用二阶迎风格式，时间离散采用中心差分格式。雷诺平均N-S方程的守恒形式可以表示为：

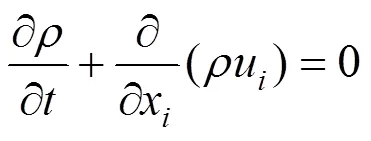
式中为空气密度；为时间；x为方向上的位置；u为方向上的空气速度。

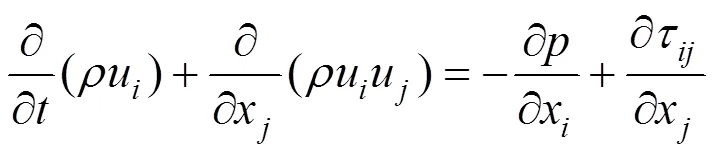
式中x为方向上的位置；u为方向上的空气速度；为空气压力；τ为雷诺应力。

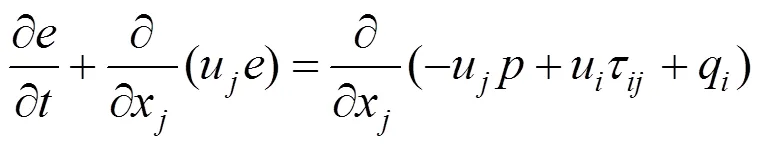
式中为动能；q为热传导率。

降落伞强度空投模型的轴向力系数A可以表示为：

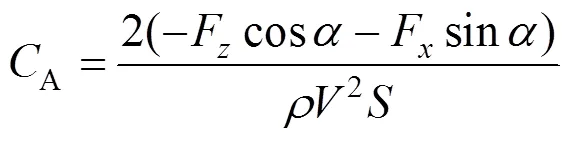
式中为飞行攻角；F为方向上的气动力，F为方向上的气动力；为来流速度；为空投模型参考面积。

降落伞强度空投模型的法向力系数N可以表示为：

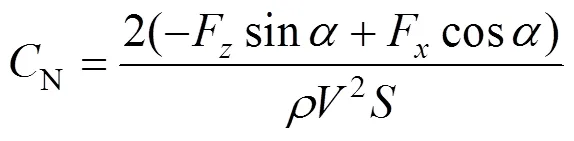
降落伞强度空投模型的俯仰力矩系数m可以表示为：

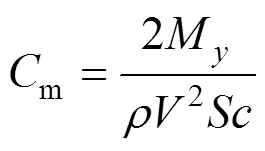
式中M为降落伞空投模型所受的俯仰力矩；为空投模型参考长度。

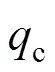
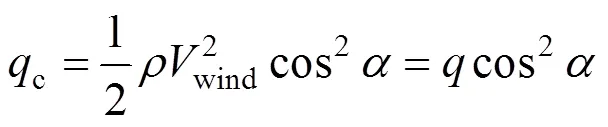
式中wind为实际气流速度；为空投试验模型实际开伞时的当地动压。

1.2 动力学仿真

考虑到降落伞强度空投试验模型的投放高度较低、飞行马赫数较小、飞行时间较短，因此飞行动力学计算中忽略地球的曲率和旋转，把大地当做平面，建立地面坐标系eee，该坐标系即为惯性坐标系XYZ。坐标原点位于强度模型投放时刻模型在平面大地上的投影点，轴位于水平面内指向空投直升机的飞行方向，轴垂直于水平面指向强度试验模型，轴按照右手坐标系规则确定。本体坐标系bbb是建立在降落伞强度空投试验模型质心处的坐标系，轴沿着纵向对称轴指向模型头部，轴垂直于轴、在投放初始时刻指向吊挂直升机，轴按照右手规则确定。

采用六自由度飞行弹道动力学方程来求解降落伞强度空投模型的弹道轨迹及运动姿态。在惯性坐标系XYZ下，降落伞强度空投模型质心运动矢量形式的微分方程可以表示为：

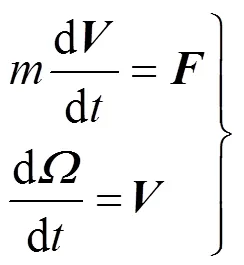
式中为空投模型质量；为空投模型质心在惯性坐标系XYZ下的速度矢量；为空投模型质心在惯性坐标系XYZ下的位置矢量；为空投模型所受的合力（包括气动力、重力等）。

在空投模型本体坐标系bbb下建立姿态运动矢量形式的微分方程：

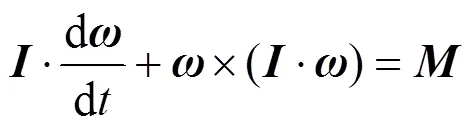
式中为空投模型的惯性张量；为空投模型在本体坐标系bbb下的角速度；为本体坐标系bbb下外力对空投模型质心的合力矩。

2 计算模型

2.1 CFD计算模型

本体坐标系bbb下降落伞强度空投试验模型的几何外形示意，如图1所示。空投模型为某航弹模型，采用X型尾翼设计。地面坐标系eee下空投模型的CFD数值仿真模型和计算网格示意，如图2所示。CFD仿真采用结构网格计算，网格总数118.8万，单元通量计算方法使用有限体积法。计算域网格保持光滑、正交，近固壁面第一层网格的y+<10，同时启用自动壁面函数，确保在局部y+过大时使用壁面函数法计算附面层流动切向速度，满足边界层流动精确模拟要求。考虑到降落伞强度空投试验的飞行速度较低（40m/s），其周围流场为不可压流动，因此湍流模型选用剪切应力输运（Shear Stress Transport，SST）模型。流场边界条件选用三方向速度、总温进口边界条件、静压出口边界条件以及无滑移绝热固壁边界条件。

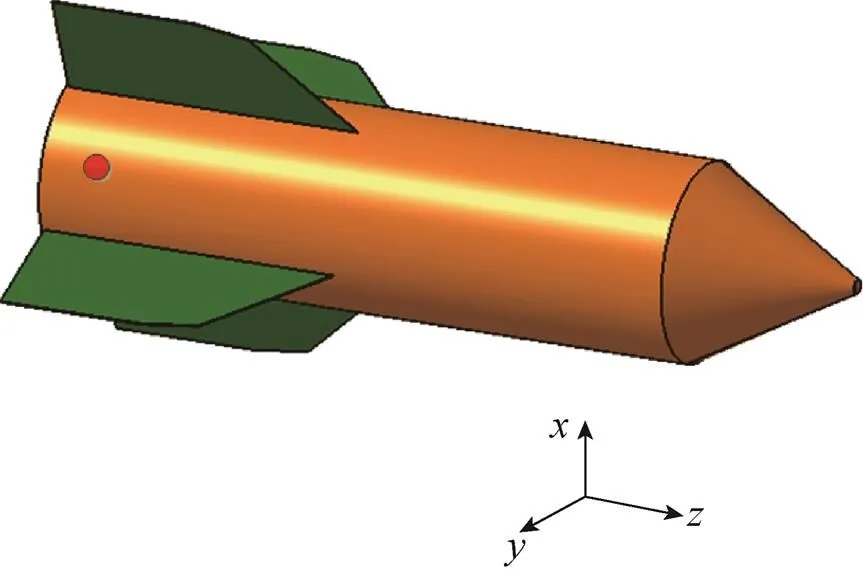
图1 降落伞空投试验模型几何外形示意

图2 CFD数值仿真模型和计算网格

2.2 动力学计算模型

降落伞强度空投试验模型的动力学计算采用MATLAB软件自编程序实现。动力学仿真计算采用如下假设：

1）假设空投模型投放前，空投直升机处于平飞状态，无垂向速度分量；

2）假设投放时刻空投直升机飞行方向朝北；

3）空投模型投放过程中，忽略地球自转，忽略地球曲率；

4）动力学计算仅考虑平面风的风速影响，忽略垂直风和风切变的影响；

5）大气密度、温度和风速数据均采用北纬40°东经90°处历年测量平均数差值获取；

6）假设输入参数的分布类型均为正态分布。

动力学计算的初始条件包括：

1）空投试验模型初始投放条件，主要有投放速度、投放高度、风速；

2）空投试验模型的质量、质心及转动惯量；

3）空投试验模型控制参数，主要有时间误差、动压误差等。

3 气动特性分析

3.1 仿真工况

降落伞空投试验模型气动性能仿真的大气高度为3 500m，初始飞行速度为40m/s，飞行攻角为0°~16°，飞行侧滑角为0°；降落伞空投试验模型的参考面积为0.95m2，参考长度为1.1m。由于降落伞空投模型为轴对称模型，因此正、负攻角下空投模型气动特性参数的绝对值相同。

3.2 流场结构分析

为分析降落伞强度空投试验模型的流场结构特征，对不同攻角下空投试验模型流场的压力分布情况进行分析。图3~图5展示了在0°、8°、16°飞行攻角下，空投试验模型子午面压力分布图。由图可知：=0°时降落伞空投试验模型的压力分布呈现上下对称的特点，在空投模型的锥顶附近存在局部高压区，而空投模型火箭锥底部的压力相对较低；正攻角飞行时，由于降落伞空投试验模型上表面附近气流绕流速度较高，下表面附近气流绕流速度较低，因此空投试验模型下表面附近的流场压力较大；相对于=0°的情况，=8°，=16°时空投试验模型锥顶附近的局部高压区向下表面后侧移动，且尾部稳定翼附近存在另一个局部高压区。

图3 α=0°时空投试验模型子午面的压力分布

图4 α=8°时空投试验模型子午面的压力分布

图5 α=16°时空投试验模型子午面的压力分布

3.3 性能参数分析

根据气动仿真流场结构分析的结果对降落伞强度空投试验模型的表面压力分布进行积分，经过坐标转换，将全局坐标系下的气动力转换至空投试验模型弹体坐标系下，得到不同攻角下空投试验模型轴向力系数、法向力系数、俯仰力矩系数的变化趋势。

图6为空投试验模型轴向力系数的攻角特性曲线。由图可知：当=0°~4°之间时，轴向力系数基本不变，维持在0.415左右的水平；当4°时，轴向力系数随攻角增加而下降；当10°时，轴向力系数下降十分显著。

图7为空投试验模型法向力系数的攻角特性曲线，图8为空投试验模型俯仰力矩系数的攻角特性曲线。由图7和图8可知：空投试验模型的法向力系数和俯仰力矩系数随着攻角增加呈现近似线性增大的趋势；在大飞行攻角时，法向力系数和俯仰力矩系数增加明显。

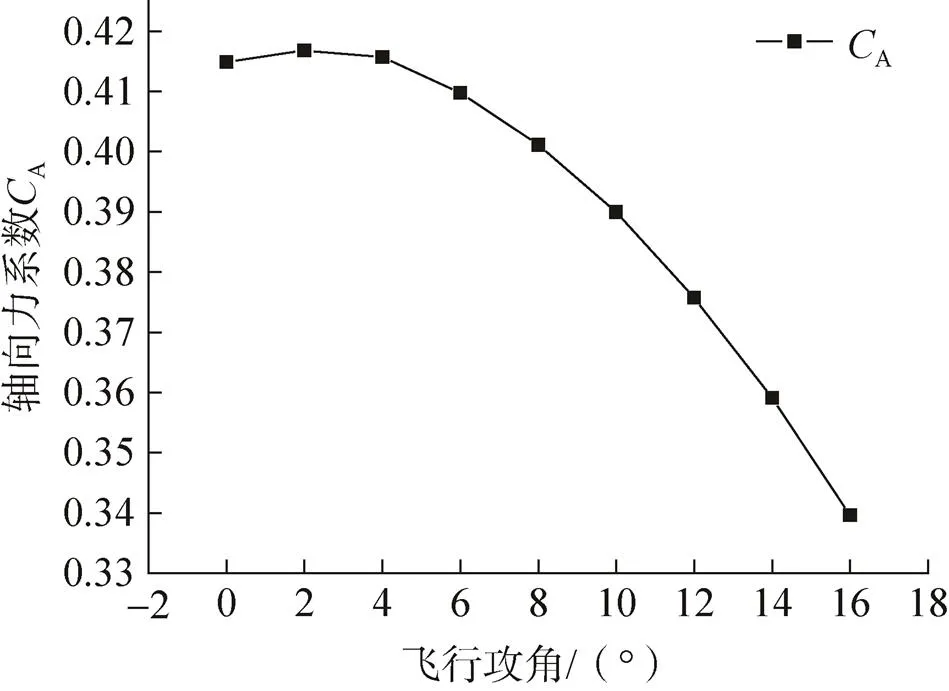
图6 空投试验模型轴向力系数的攻角特性曲线

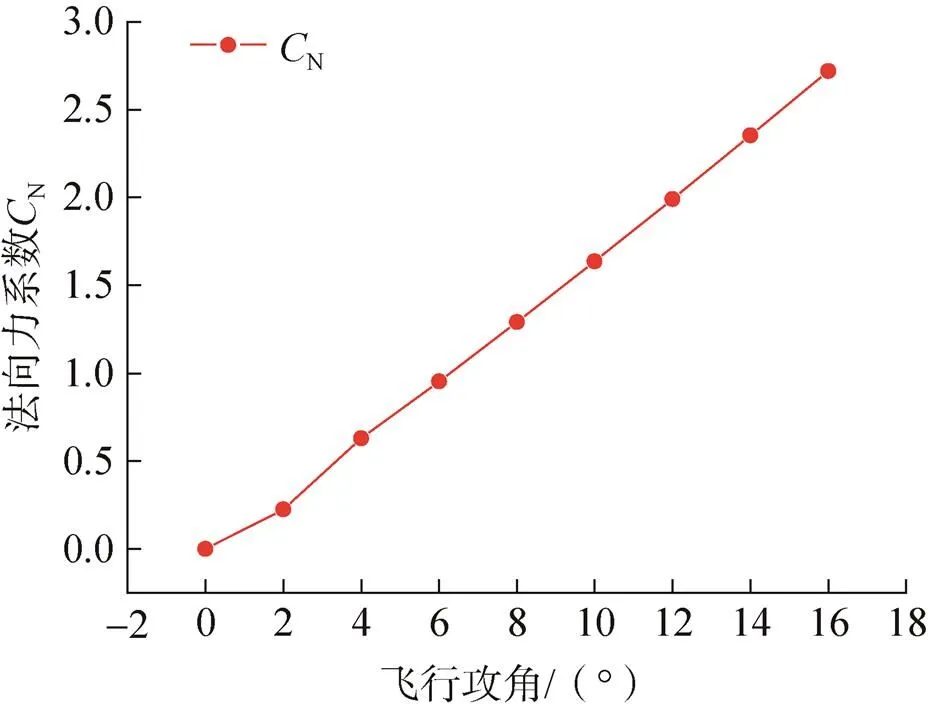
图7 空投试验模型法向力系数的攻角特性曲线

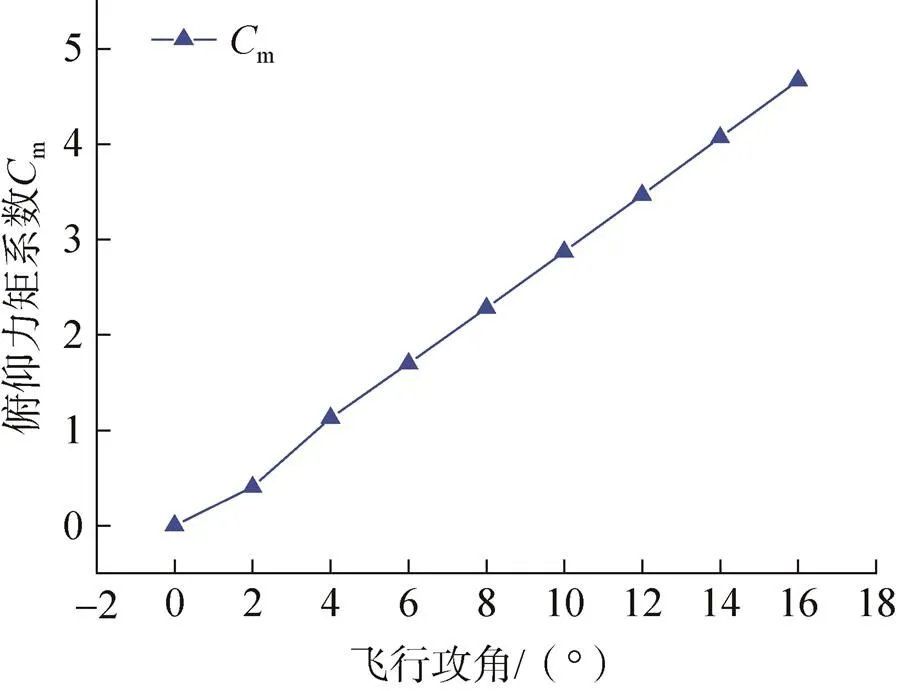
图8 空投试验模型俯仰力矩系数的攻角特性曲线

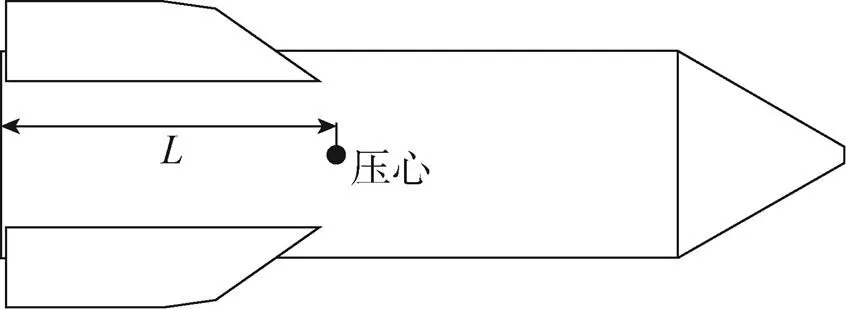
图9 空投试验模型的压心位置示意

根据法向气动力和俯仰力矩的仿真结果确定降落伞强度空投试验模型的压心位置。以空投试验模型尾部端面为参考面，图9展示了压心位置的示意，图中代表压心位置距参考面的距离。图10展示了不同飞行攻角下压心位置的变化趋势。由图10可知：随着飞行攻角增加，空投试验模型的压心位置后移，且重心位置始终位于压心位置之前，空投试验模型的气动稳定性良好。

4 动力学特性分析

在气动仿真得到各项气动特性参数的基础上进一步开展动力学仿真分析，对不开伞情况下的标称弹道进行计算，在忽略动力学计算各初始条件参数的误差项、仅考虑标称值的情况下分析降落伞强度空投试验模型的弹道轨道和运动姿态，动力学计算时间总共持续约25s。

图11展示了空投试验模型不开伞情况下标称弹道的仿真结果。由图可知：模型投放后，随着高度下降空投试验模型的速度以近似线性的形式增大；空投试验模型的最大飞行攻角为16°，投放后空投模型的俯仰角和攻角均存在摆动现象，摆动周期约为3s。

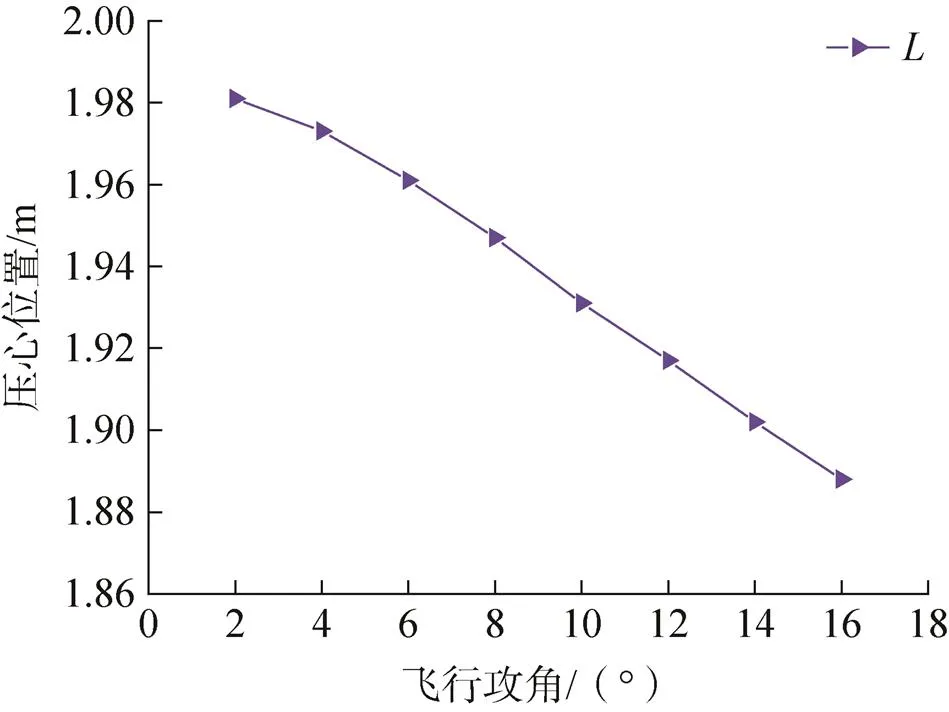
图10 不同飞行攻角下压心位置变化趋势

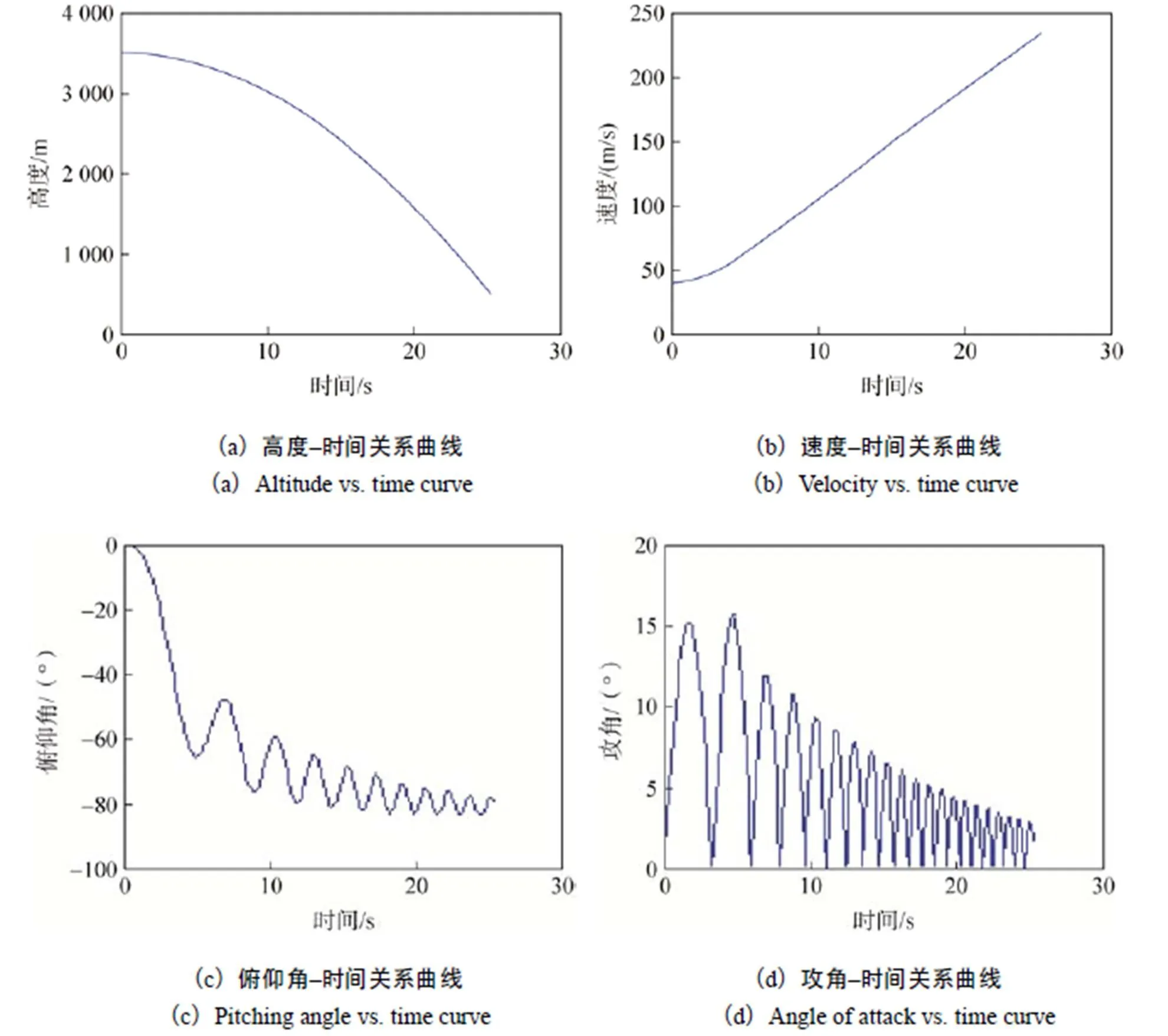
图11 空投试验模型不开伞情况下标称弹道的仿真结果

取空投试验模型飞行攻角第一个摆动周期之内的动压情况进行分析，结果如图12所示。由图可知：以目标开伞动压750Pa计算，空投试验模型达到开伞动压时的飞行攻角约为15°。

降落伞强度空投试验模型的头部安装有空速管。由于空速管测量得到的动压值为实际气流动压沿其轴线方向的投影分量，因此降落伞强度空投试验模型的飞行攻角对空速管动压测量值有一定影响。空速管动压测量值与实际开伞动压的相对偏差值随空投试验模型飞行攻角的变化趋势如图13所示。由图可知，空投试验模型的飞行攻角越大，空速管动压测量值与实际开伞动压的相对偏差越显著。按目标开伞动压750Pa计算，若实际开伞时空投试验模型的飞行攻角达到16°，则空速管测得的动压值为812Pa，空速管动压测量值与实际开伞动压的相对偏差值为0.08。

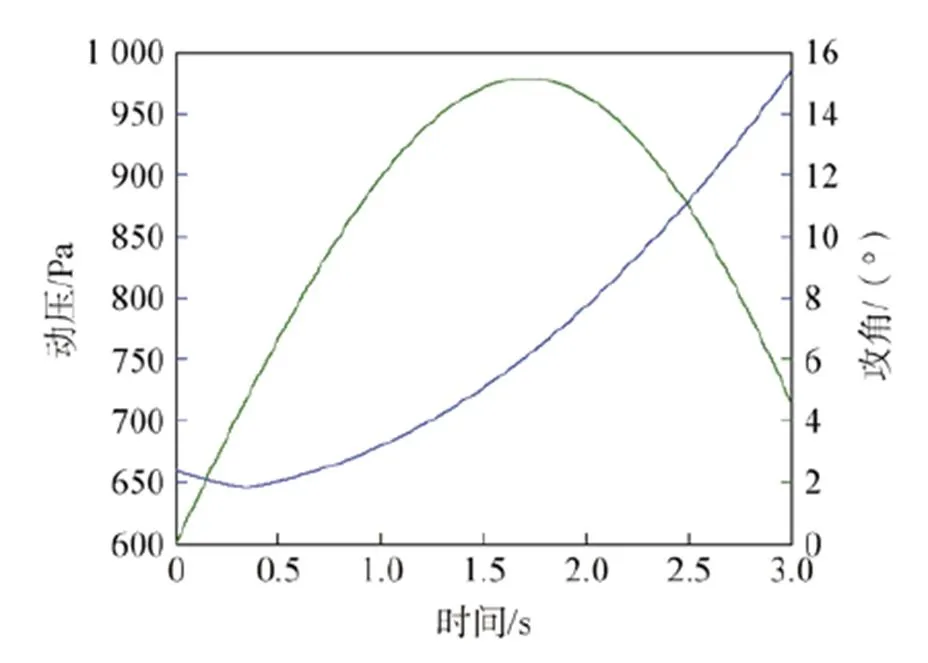
图12 空投试验模型飞行攻角第一个摆动周期之内的动压变化曲线

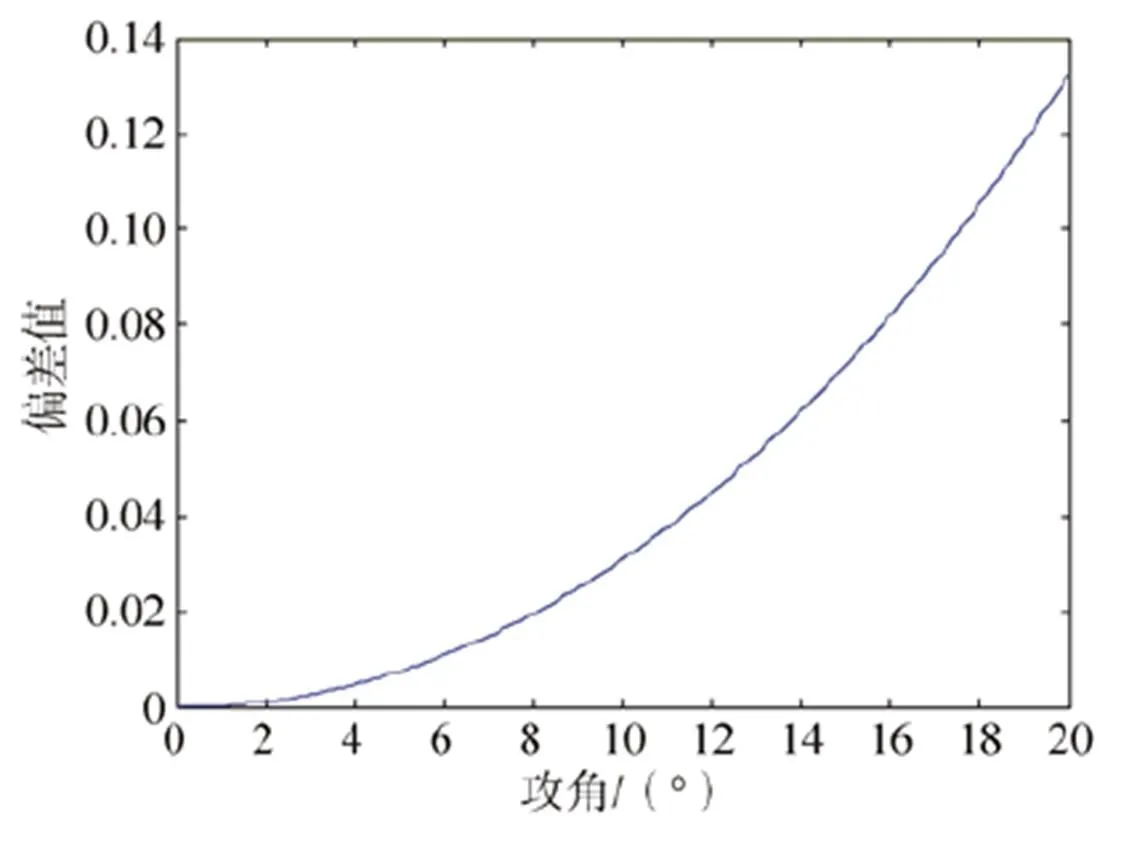
图13 空速管动压测量值与实际开伞动压的相对偏差值随飞行攻角的变化趋势

在动力学仿真中对空投试验模型进行开伞前的偏差弹道分析，主要考虑如下参数的偏差影响：空投试验投放速度、高度偏差及风速影响，模型质量、质心、转动惯量偏差，时间偏差等。除上述参数外，偏差弹道分析还考虑了投放时刻空投试验模型欧拉角的偏差范围，其中俯仰、偏航和滚转角的偏差范围均按±5°（3）考虑，参数分布类型为正态分布。

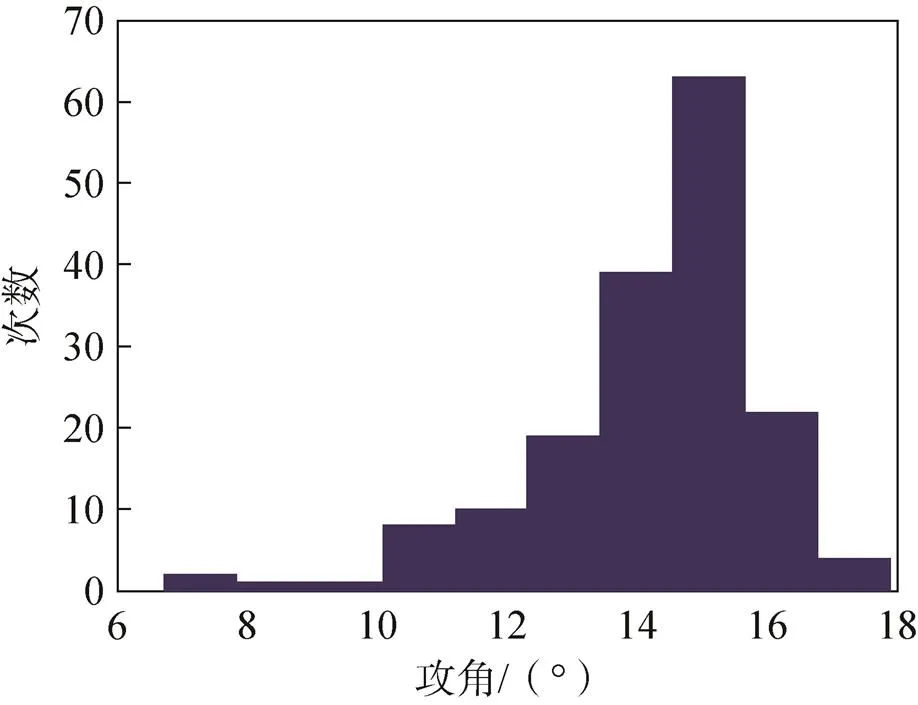
图14 空速管测量得到750Pa动压时空投试验模型的飞行攻角分布直方图

偏差弹道分析共运算200次，对空速管测量得到750Pa动压时空投试验模型的飞行攻角分布进行统计，统计结果如图14所示。由图可知：空速管测得750Pa开伞动压时，空投试验模型飞行攻角的均值约为14°，3范围约为5°，因此飞行攻角的分布范围约为9°~19°。结合图13进行分析，飞行攻角影响下实际开伞动压与空速管测量值的相对偏差范围不会超过0.14。

5 结束语

本文对降落伞强度空投试验模型开展了气动仿真和动力学仿真，分析了空投试验模型的阻力特性和气动稳定性，探讨了降落伞开伞前空投试验模型的弹道轨迹和运动姿态的变化，并针对不同飞行攻角下空速管动压测试值与实际开伞动压存在相对偏差所造成的影响进行了分析。主要得出以下结论：

1）随着飞行攻角增加，空投试验模型的气动特性参数有所改变：法向力系数和俯仰力矩系数近似线性增大，轴向力系数在4°以上攻角有所下降，压心位置向后移动，空投试验模型的压心位置始终位于重心之后，气动稳定性较好；

2）在模型投放后至降落伞开伞前的过程中，随着高度下降空投试验模型的速度以近似线性的形式增大，空投试验模型的俯仰角和攻角均存在周期摆动现象；

3）由于飞行攻角的影响，空速管测得的动压值与开伞实际动压存在一定的相对偏差，通过偏差弹道分析可知，飞行攻角影响下实际开伞动压与空速管测量值的相对偏差范围不会超过0.14。

[1] 王海涛, 秦子增, 宋旭民, 等. 大型降落伞拉直过程中的抽打现象分析[J]. 国防科技大学学报, 2010, 32(5): 34-38. WANG Haitao, QIN Zizeng, SONG Xumin, et al. Analysis of the Phenomenon of Bull Whipping in the Deployment Process of Large Parachute[J]. Journal of National University of Defense Technology, 2010, 32(5): 34-38. (in Chinese)

[2] 宋旭民, 程文科, 彭勇, 等. 飞船回收过程动力学建模与仿真[J]. 弹道学报, 2005, 17(2): 55-59. SONG Xumin, CHENG Wenke, PENG Yong, et al. Dynamic Modelization and Simulation of Spaceship Recovery Scenario[J]. Journal of Ballistics, 2005, 17(2): 55-59. (in Chinese)

[3] 荣伟, 陈旭, 陈国良. 火星探测用降落伞研制试验简介[J]. 航天返回与遥感, 2007, 28(1): 172-178. RONG Wei, CHEN Xu, CHEN Guoliang. Resume of the Tests about Parachute Development for Mars Exploration Mission[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(1): 172-178. (in Chinese)

[4] 黄伟. 运载火箭伞降回收着陆技术概述[J]. 航天返回与遥感, 2017, 38(3): 1-12. HUANG Wei. The Summary of Launch Vehicle Parachute Recovery and Landing Technologies[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(3): 1-12. (in Chinese)

[5] 王利荣. 降落伞理论与应用[M]. 北京: 宇航出版社, 1997: 604-611. WANG Lirong. Theory and Application of Parachute[M]. Beijing: China Astronautics Publishing House, 1997: 604-611. (in Chinese)

[6] STEIN K R, BENNEY R J, TEZDUYAR T E. Fluid-structure Interactions of a Round Parachute: Modeling and Simulation Techniques[J]. Journal of Aircraft, 2001, 38(5): 800-808.

[7] 余莉, 明晓, 胡斌. 降落伞开伞过程的试验研究[J]. 南京航空航天大学学报, 2006, 38(2): 176-180. YU Li, MING Xiao, HU Bin. Experimental Investigation in Parachute Opening Process[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2006, 38(2): 176-180. (in Chinese)

[8] 柯鹏, 杨春信, 杨雪松, 等. 重型货物空投系统过程仿真及特性分析[J]. 航空学报, 2006, 27(5): 856-860. KE Peng, YANG Chunxin, YANG Xuesong, et al. System Simulation and Analysis of Heavy Cargo Airdrop System[J]. Acta Aeronautica EtAstronautica Sinica, 2006, 27(5): 856-860. (in Chinese)

[9] 徐宏, 曹义华. 降落伞典型开伞过程的试验研究[J]. 飞行力学, 2012, 30(1): 74-78. XU Hong, CAO Yihua. Experimental Investigation in Typical Parachute Opening Process[J]. Flight Dynamics, 2012, 30(1): 74-78. (in Chinese)

[10] DESABRAIS K J. Velocity Field Measurements in the Near Wake of a Parachute Canopy[D]. Massachusetts: Worcester Polytechnic Institute, 2002.

[11] 杨雪松, 王乘, 李振环. 超低空空投过程的仿真[J]. 华中科技大学学报(自然科学版), 2003, 31(4): 108-110. YANG Xuesong, WANG Cheng, LI Zhenhuan. Simulation of Airdropping at a Super-low-altitude[J]. Journal of Huazhong University of Science and Technology(Nature Science Edition), 2003, 31(4): 108-110. (in Chinese)

[12] 戴正升. 超低空空投重装货物出舱过程飞行控制技术研究[D]. 南京: 南京航空航天大学, 2012. DAI Zhengsheng. Flight Control Technology Research for Heavy Cargo Extraction of Super Low Altitude Airdrop[D]. Beijing: Nanjing University of Aeronautics and Astronautics, 2012. (in Chinese)

[13] 杨妙升, 屈香菊. 运输机空投的飞行动力学建模与仿真[J]. 飞行力学, 2010, 28(3): 9-12. YANG Miaosheng, QU Xiangju. Flight Dynamic Modeling and Simulation for Transport Airdrop[J]. Flight Dynamics, 2010, 28(3): 9-12. (in Chinese)

[14] 雷娟棉, 牛健平, 王锁柱, 等. 初始分离条件对航弹与载机分离安全性影响的数值模拟研究[J]. 兵工学报, 2016, 37(2): 357-366. LEI Juanmian, NIU Jianping, WANG Suozhu, et al. Numerical Simulation about the Effect of Initial Separation Condition on Safety of Aerial Bomb Separated from an Aircraft[J]. Acta Armamentarii, 2016, 37(2): 357-366. (in Chinese)

[15] 王学, 冯志刚, 高普云, 等. 降落伞可靠性评定及其试验量决策[J]. 宇航学报, 2010, 31(6): 1685-1689. WANG Xue, FENG Zhigang, GAO Puyun, et al. Parachute Reliability Assessment and Decision——Making of Experiment Times[J]. Journal of Astronautics, 2010, 31(6): 1685-1689. (in Chinese)

[16] 毛强. 降落伞空投试验测试系统的研制[J]. 测控技术, 2004, 23(1): 72-75. MAO Qiang. Development of the Test System for Parachute[J]. Measurement and Control Technology, 2004, 23(1): 72-75. (in Chinese)

[17] 张海妮, 张培田, 程伟豪. 两种空投建模方法的研究[J]. 科学技术与工程, 2012, 12(16): 3896-3900. ZHANG Haini, ZHANG Peitian, CHENG Weihao. Research of Two Different Modeling Methods of Airdrop[J]. Science Technology and Engineering, 2012, 12(16): 3896-3900. (in Chinese)

[18] 孙秀霞, 徐光智, 刘日, 等. 航空运输物资空投过程动力学模型[J]. 交通运输工程学报, 2016, 16(2): 125-131. SUN Xiuxia, XU Guangzhi, LIU Ri, et al. Dynamics Model of Airdrop Process for Air Transportation Cargo[J]. Journal of Traffic and Transportation Engineering, 2016, 16(2): 125-131. (in Chinese)

（编辑：陈艳霞）

Numerical Simulation on Aerodynamic & Dynamic Characteristics of Parachute Airdrop Test Model

ZHANG Zhang1,2,3WANG Liwu1WANG Wenqiang1WANG Qi1LYU Zhihui1LI Jian1

（1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）（2 Key Laboratory for Nondestructive Spacecraft Landing Technology of CAST, Beijing 100094, China）（3 Beijing Engineering Technology Research Center of Aerial Intelligent Remote Sensing Equipments, Beijing 100094, China）

Aerodynamic and dynamic numerical research of parachute airdrop model is a main concern for airdrop test design and parachute deceleration system performance evaluation. In this paper, aerodynamic characteristics and stability of the airdrop test model are investigated, trajectory and motion posture are also discussed. Furthermore, the influence induced by dynamic pressure relative deviation between the measurement value of airspeed head and real value when parachute opening in different angles of attack are also analyzed in this paper. The result shows axial force coefficient decreases when angle of attack is above 4°. Normal force coefficient and pitching moment coefficient have a linear increment with angle of attack increases. The aerodynamic stability is high enough and the airdrop test center of pressure location moves back with the angle of attack increases. After airdrop test model extraction and before parachute opening, the velocity of airdrop test model has a linear increment with altitude declines, and there is a periodic oscillation in angle of pitch and angle of attack. Since the influence of angle of attack, there is dynamic pressure relative deviation between the measurement value of airspeed head and real value when parachute opening. However, the relative deviation range is not more than 14%. The research result can be applied in parachute airdrop test design.

parachute airdrop test; aerodynamic performance; dynamic charanteristics; dynamic pressure deviation; numerical simulation; space recovery

V211.3

A

1009-8518(2018)01-0001-10

10.3969/j.issn.1009-8518.2018.01.001

张章，男，1986年生，2014年获北京航空航天大学流体机械及工程专业博士学位，高级工程师。主要研究方向为航天器返回与着陆技术及空气动力学。E-mail：xiaodanni198649@sina.com。

2017-10-28

国家自然科学基金（11602018）