基于协方差矩阵重构的稳健自适应波束形成算法

王 昊，马启明

(杭州应用声学研究所，浙江 杭州 310023)

0 引言

自适应波束形成技术可以广泛地应用于雷达、声纳、无线通信等众多领域。在理想条件下，即阵元协方差矩阵精确已知，导引向量(SV，Steering Vector)准确无误差的情况下，是输出信干噪比(SINR，Signal-to-Interference-Plus-Noise Ratio)最大准则下最优的空域滤波器。然而，在实际应用环境中，阵列快拍数往往有限，利用有限快拍得到的采样协方差矩阵与理论值存在误差，另一方面，波束指向角度失配会导致导引向量误差，特别是大角度失配情况下，自适应波束形成器性能严重下降[1]。

现有的基于标准Capon波束形成器[2](SCB，Standard Capon Beamformer)的稳健自适应波束形成算法，以Cox提出白噪声增益约束法[3]最为著名，然而，不同工作环境下最优对角加载量的选取是一个十分困难的问题。稳健Capon波束形成器[4](RCB，Robust Capon Beamformer)是目前较为流行的稳健自适应波束形成算法，但是，它无法解决训练数据包含期望信号的问题，依然存在信号“自消”的风险，同时在波束指向角失配较大时，算法性能严重下降[5-6]。文献[7]算法可以提高自适应波束形成器在角度失配条件下稳健性。然而，在信噪比较高时，会出现信号“自消”现象。文献[8]基于干扰噪声协方差矩阵重构，提出了一种区别于对角加载类算法的新思路，但是，在大角度失配时，导引向量估计不准确，由此会造成输出信噪比的损失[9]。另外现有的许多稳健自适应算法[10-11]，需要求解半定规划、二阶锥规划，都用到解最优化问题的工具箱[12]，这就给算法的实用性带来了不便。

综上可知，在大角度失配和采样协方差矩阵中包含有期望信号时，传统自适应波束形成器的性能将极剧下降。此时，如何提高自适应波束形成器的稳健性是一个亟需研究的问题。本文针对此问题，提出了基于协方差矩阵重构的稳健自适应波束形成算法。

1 阵列信号模型

考虑基阵模型，阵元个数为M，假设有Q个窄带信源同时入射到阵列，信源之间相互独立，则阵元接收信号的第k个快拍为：

x(k)=xs(k)+xj(k)+n(k)

(1)

其中，xs(k)表示期望信号成分，xj(k)表示Q-1个干扰成分，n(k)为与信源相互独立的空时高斯白噪声。

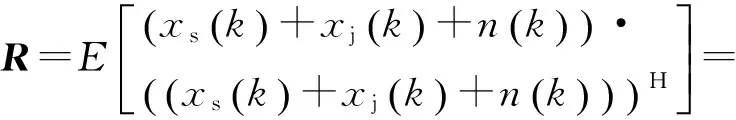
(2)

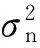
R=Rs+Rj+n

(3)

建立最优化准则

(4)

可以得到最大化输出信干噪比准则下的最优权值w。上式可等价为：

(5)

此式即标准Capon波束形成器，由此可得最优权值为

(6)

利用求解出的最优权值可以得到标准Capon波束形成器的输出功率为：

(7)

(8)

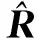
2 基于协方差矩阵重构的稳健自适应波束形成算法

2.1 干扰加噪声协方差矩阵重构

当期望信号包含于阵列数据中时，利用采样协方差矩阵代替干扰噪声协方差矩阵，常常会出现信号“自消”现象，导致自适应波束形成器性能的急剧下降，为此这里提出一种干扰加噪声协方差矩阵重构方法。

(9)

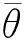
(10)

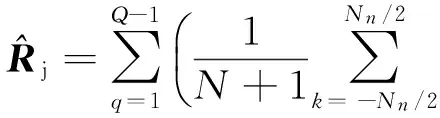
(11)

其中，Nn表示对感兴趣区域的划分点数，可以根据空间区域的大小范围以及基阵波束宽度或粗或细的进行划分。

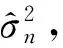
(12)

2.2 期望信号导引向量估计

将采样协方差矩阵写成子空间形式

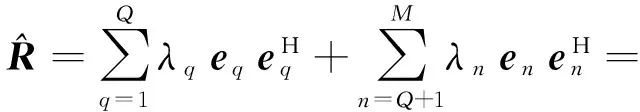
(13)

MUSIC算法是利用噪声子空间与导引向量的正交性构造空间谱，理想情况下，其空间谱是一个狄拉克δ函数(定义为在目标方位呈现出峰值，而在非目标方向上均为0)。由此利用MUSIC谱估计法重构信号协方差矩阵

(14)

(15)

即可得到估计的期望信号导引向量

(16)

在求取最大特征值及其对应的特征向量时，可以利用乘幂法[15]等迭代算法降低运算量。

(17)

3 仿真与性能分析

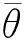
仿真一：考察算法的输出信干噪比随输入信噪比的变化。快拍数固定为K=50，每种SNR条件下进行100次独立重复实验，统计平均SINR。

由上图可以看出SCB受期望信号导引向量估计误差以及期望信号的影响，性能严重偏离理论最优值，这种性能恶化随着输入信噪比的增加不断增大。RCB和文献[7]算法相较SCB，性能均有所改善，然而由于利用包含期望信号的采样协方差求取最优权值，随着信噪比的增大，性能恶化，在低信噪比情况下，文献[7]算法由于导引向量估计偏差，性能甚至劣于SCB，文献[8]算法由于利用重构的干扰加噪声协方差矩阵求取最优权值，避免了信号“自消”现象的发生，但是由于期望信号角度失配较大，求解最优化得到的导引向量不准确，性能偏离了理论最优。相较前述几种方法，本文所提算法的SINR最高，与理论最优误差最小。然而可以看出，在极低信噪比(SNR<-10 dB)情况下，本文方法亦偏离了理论最优，这是由于低信噪比条件下，子空间划分不准确导致的导引向量估计偏差引起的，后续将针对此开展相关工作。

仿真二：考察算法的输出信干噪比随快拍数的变化。假设期望信号的信噪比为5 dB，快拍数在K=[10∶4∶100]之间变化，同样地，每种快拍数下进行100次独立重复实验，统计平均SINR，观察几种算法的输出SINR随快拍数变化的曲线。

由上图可知，由于大角度失配，SCB随快拍数的增加，性能急剧恶化，RCB和文献[7]算法相较SCB有所改善；SINR随快拍数的增加而增加，然而由于期望信号的影响，SINR与理论最优始终有较大差距；文献[8]算法，受快拍数影响较小，相较前述几种方法收敛速度快，SINR高于前述方法，然而由于大角度失配导致的期望信号导引向量估计不准确，SINR依然偏离理论最优；本文所提算法由于采用了重构协方差矩阵，避免了由于快拍数有限，波束形成器性能下降的问题，同时，本文所提算法由于采用了子空间理论，在采样协方差矩阵不满秩时，即可得到噪声子空间的估计，进而得到期望导引向量的估计值；而文献[7]和文献[8]需要在快拍数N≥M的条件下才能得到期望导引向量的估计，故而本文算法需要的快拍数更小，收敛速度更快，在相同快拍数情况下，SINR最高，性能最好。

仿真三：考察不同算法的波束图。假设期望信号的信噪比为5 dB，快拍数K=50，画出不同算法的归一化波束图。

由上图可以看出，RCB算法和文献[8]算法由于大角度失配，主瓣指向方向偏差，在期望信号真实入射方向附近产生了零陷；文献[7]算法的主瓣虽然指向了真实入射方向，但是由于快拍数有限，因而具有很高的旁瓣；本文方法由于采取了干扰加噪声协方差矩阵重构以及期望信号导引向量估计，故而纠正了主瓣指向，避免了期望信号方向出现零陷，同时没有抬高旁瓣级。

仿真四：考察不同角度失配条件下算法的性能。假设期望信号的信噪比为5 dB，快拍数为K=50，期望信号以及两个干扰的角度失配在[-6∶1∶6]之间变化，每种失配角度下进行100次独立重复实验，统计平均SINR，观察几种算法的输出SINR随角度失配变化的曲线。

可以看出SCB与文献[7]以及RCB受采样协方差矩阵当中期望信号成分的影响，输出SINR均不同程度的偏离理论最优值；文献[8]优于前述方法，但是在大角度失配条件下，求解最优化得到的导引向量不准确，导致性能偏离理论最优；本文方法性能优于其他几种算法，在不同角度失配条件下，性能均接近理论最优值。

4 结论

本文提出了基于协方差矩阵重构的稳健自适应算法，该算法将全空域划分成若干互不重叠的区域，分别对应干扰区域和期望信号区域，先利用标准Capon波束形成器及采样协方差矩阵的最小特征值对干扰加噪声协方差矩阵进行重构，再利用MUSIC谱估计法重构出信号协方差矩阵，以其主特征向量估计出期望信号导引向量，最终得到自适应波束形成器的最优权值。仿真实验结果表明，算法能够避免训练数据包含有期望信号和导引向量角度失配引起的自适应波束形成器性能下降的问题，在大角度失配和少快拍数的情况下具有良好的性能。

[1]EHRENBERG L, GANNOT S, LESHEM A,et al. Sensitivity analysis of MVDR and MPDR beamformers[C]//2010 IEEE 26th Convention of Electrical and Electronics Engineers, Eilat, Israel, 2010: 416-420.

[2]Capon J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE,1969,57(8):1408-1418.

[3]COX H, ZESKIND R M, OWEN M. Robust adaptivebeamforming[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1987, 35(10):1365-1376.

[4]LI J, STOICA P, WANG Z. On robust Caponbeamforming and diagonal loading[J]. IEEE Transactions on Signal Processing, 2003, 51(7):1702-1715.

[5]NAI S E, SER W, YU Z L,et al. Iterative robust minimum variance beamforming[J]. IEEE Transactions on Signal Processing, 2011, 59(4):1601-1611.

[6]LIE J P, SER W, SEE C M S. Adaptive uncertainty based iterative robust capon beamformer using steering vector mismatch estimation[J]. IEEE Transactions on Signal Processing, 2011, 59(9):4483-4488.

[7]ZHANG W, WANG J, WU S. Robust caponbeamforming against large DOA mismatch[J]. Signal Processing, 2013, 93(4):804-810.

[8]GU Y, LESHEM A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J]. IEEE Transactions on Signal Processing, 2012, 60(7):3881-3885.

[9]KHABBAZIBASMENJ A, VOROBYOV S A, HASSANIEN A. Robust adaptive beamforming based on steering vector estimation with as little as possible prior information[J]. IEEE Transactions on Signal Processing, 2012, 60(6):2974-2987.

[10]KIM S J, MAGNANI A, MUTAPCIC A, et al. Robust beamforming via Worst-Case SINR maximization[J]. IEEE Transactions on Signal Processing, 2008, 56(4):1539-1547.

[11]HASSANIEN A, VOROBYOV S A, WONG K M. Robust adaptive beamforming using sequential quadratic programming: an iterative solution to the mismatch problem[J]. IEEE Signal Processing Letters, 2008, 15:733-736.

[12]GTANT B M and BOYD S. CVX: MATLAB software for disciplined convex programming [EB/OL]. [2017-07-07]http://www.stanford.end/boyd/cvx/, 2016.

[13]TREES H L. Optimum Array Processing—Part IV of Detection, Estimation, and Modulation Theory[M]. New York: Wiley, 2002: 332-333.

[14]SCHMIDT R. Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation, 1986, 34(3):276-280.

[15]沈剑华. 计算数学基础[M]. 上海：同济大学出版社, 1989.

[16]SOMASUNDARAM S D, PARSONS N H. Evaluation of robust capon beamforming for passive sonar[J]. IEEE Journal of Oceanic Engineering, 2011, 36(4):686-695.