MEMS悬臂卡锁式后坐保险机构
2018-03-12李雯迪聂伟荣席占稳陈海峰
李雯迪,聂伟荣,席占稳,陈海峰
(南京理工大学机械工程学院,江苏 南京 210094)
0 引言
微机电系统(Micro Electro-mechanical System,MEMS)是集微机械结构和微电子于一体的微型集成化系统,如微传感器、微陀螺仪、微马达等其他执行器,具有采集、处理和传递信息等功能。相比于传统机电系统,因具有尺寸小、易集成以及大批量生产等优点得到了迅速发展,已在航空航天、汽车电子、国防事业、生物医学和环保等人们所接触到的几乎所有领域都有着广泛的应用前景[1-4]。
近年来随着新技术的不断涌入,新的战场环境的不断拓展,对引信的要求也不断地提高,同时,现代武器装备对弹药性能及毁伤效能要求也在不断提高。这就要求在现有弹药的固有体积中,增大装药量并压缩引信的空间[5]。采用MEMS技术可有效地降低在有限空间内设计复杂功能引信的难度并增强引信的功能,MEMS技术应用于引信的一个重要方向就是MEMS安全系统。MEMS技术在引信安全系统中应用最早始于美国海军水面作战中心(NSWC)研制的6.25 in反鱼雷引信[6],并成功对该装置进行了海上射击试验。Charles H.Robinson团队对MEMS技术在引信安全系统中的应用做了大量的工作,设计的MEMS安保机构历经几代,技术比较成熟,用于理想单兵战斗武器系统中的MEMS安保机构已经进行了多次实弹射击,其主要设计思路[7]是,模块化的MEMS安全系统,主要采用UV-LIGA工艺,材料选用镍基或者铜基,采用后坐和离心双保险,同时,第二道远距离解除保险都采用电火药执行器对其进行动作控制,传爆序列采用错位式。文献[8]提出了包含滑块、弹簧以及闭锁机构MEMS后坐保险机构,通过仿真分析表明该后坐保险机构满足某小口径榴弹的使用要求。程玄玄等人[9]提出了一种剪断式后坐卡销MEMS保险机构,验证了该后坐卡销解除保险行程较大,满足可靠性要求。
但上述MEMS安全系统都是采用单片式设计思想[10],安全系统平行弹轴进行放置,使得传爆序列与传统引信相垂直,传爆序列不在同一直线上,爆轰能量的传递需要改变方向,必然会带来能量的损失。本文针对上述问题,提出了可用于垂直于弹轴放置的MEMS安全系统的悬臂卡锁式后坐保险机构。
1 MEMS安全系统工作原理
本文中提出的一种垂直于弹轴放置的MEMS安全系统整体结构如图1,该系统主要由基板、悬臂卡锁式后坐保险机构、离心保险机构、隔爆滑块、指令锁保险机构[11]等组成。MEMS安全系统是采用MEMS技术在基板上一体化加工出后坐保险机构和离心保险机构,该结构的优点是一体化加工,免装配,易实现。本文提出的MEMS安全系统主要应用于中大口径榴弹等弹种之上。
MEMS安全系统的工作原理为:平时状态下,隔爆滑块被后坐保险机构和离心保险机构卡住,该系统处于安全状态;发射后,悬臂卡锁式后坐保险机构感受后坐环境力向下运动脱离隔爆滑块,解除对隔爆滑块的第一道保险;隔爆滑块在离心力的作用下向右运动解除对离心保险机构的锁定,之后在离心力的作用下离心弹性梁带动离心卡锁向外侧运动,解除对隔爆滑块的第二道保险;当弹丸飞行至炮口安全距离之外,指令锁保险机构开始作用,通过弹道实时信息控制,推动柔性锁臂,解除对隔爆滑块的最后一道保险,隔爆滑块在离心力的作用下运动到位并锁定,此时该系统处于解除保险状态,传爆序列对正,引信处于待发状态。
2 模型简化与理论分析
本文中提出的垂直于弹轴的MEMS安全系统的悬臂卡锁式后坐保险机构,其基本模型可以看成是一个弹簧支撑的悬空质量块,即弹簧质量阻尼系统,简化后的物理模型如图2所示,由于质量块的质量往往远大于弹簧的质量,在这种情况下忽略弹簧的质量引起的误差微乎其微,因此该模型由质量为m的质量块与一个无质量的、弹性系数为k的弹簧组成,阻尼系数为c,用于识别两种典型的加速度环境,即意外跌落环境和正常发射环境。为简化设计计算,设计时将采用最常见的冲击加速度形式——半正弦冲击[12]来模拟两种加速度环境,简化后如图3所示。
由于阻尼力远小于工作时的惯性力,为简化分析过程,忽略阻尼c对系统响应的影响,加速度环境下的后坐保险机构可等效为一个无阻尼单自由度受迫振动系统,即弹簧质量系统,m为系统质量块质量,k为弹簧刚度系数,x(t)为质量块的位移,a(t)为施加在系统上的激励。根据牛顿第二定律可得系统的运动学方程为:
(1)
式(1)中,半正弦冲击加速度a(t)的表达式为:
a(t)=a0sinω0t(t (2) 式(2)中,a0是幅值,t0是脉宽,t0=π/ω0,ω0是半正弦加速度的本征频率,因此式(1)可以改写成 (3) (4) 将x(t)对t求导可得 (5) 当ωn<ω0时,t=2nπ/(ωn+ω0)>t0,x(t)在区间[0,t0]上是个增函数,没有极值点,所以质量块在t0处取得最大位移 (6) 当ωn>ω0时,x(t)在t=2nπ/(ωn+ω0)处取得极大值,此时质量块的最大位移为 (7) 针对本文的设计需求,需要区分意外跌落和正常发射两种不同的激励,模拟意外跌落载荷的峰值相对较大,脉宽相对较小,结合应用背景,幅值a01=15 000g,脉宽t01=0.1~0.15 ms,正常发射情况下,幅值a02=12 000g,脉宽t02=4~6 ms,通过数值仿真得到两种加速度情况下不同脉宽对其最大位移的影响如图4所示。 从图4中可以看出,模拟意外跌落时,脉宽越大,系统最大相应位移越大;正常发射时,脉宽越小,位移越大。因此,选取意外跌落位移最大时,即幅值a01=15 000g,脉宽t01=0.15 ms与正常发射位移最小值,即幅值a02=12 000g,脉宽t02=6 ms进行比较,得到图5。 从图5中可以看出,在正常发射环境下系统的最大响应位移随着固有角频率的增加而急剧减小,而在意外跌落环境下,固有角频率的变化对系统最大响应位移的影响不明显,从图中可知,在系统的固有角频率小于7 300 rad/s时,正常发射时的最大位移响应总是大于意外跌落时的位移响应,因此理论证明,弹簧质量系统可以识别这两种环境,只要确保在意外跌落时,弹簧质量系统的位移总是小于解除保险需要的位移,在正常发射时,弹簧质量系统的位移总是大于解除保险需要的位移,就能保证意外跌落时引信处于安全状态,正常发射时引信能够可靠解除保险。 有限元仿真分析是处理动力学问题的有效方法,使用ABAQUS建立悬臂卡锁式后坐保险机构实体模型,考虑到高韧性的要求,悬臂卡锁利用微电铸工艺用镍材料制作,由于其机械性能与电铸过程中的电流密度、电铸时间、电铸面积、加工高度等因素有密切关系,加工过程不同,材料参数会有一定的差异,其屈服强度处于0.5~1.1 GPa[13-14],为便于分析,电铸镍材料的参考参数如表1。 表1 电铸镍材料参数 根据理论分析满足要求的固有频率,建立悬臂卡锁式后坐保险机构的实体模型,初步选定悬臂卡锁梁长4 mm,宽0.3 mm,厚0.1 mm,悬臂卡锁质量块为半径为1 mm 空心圆柱,厚为0.1 mm,隔爆滑块厚度为0.8 mm,如图6所示。隔爆滑块的厚度即为后坐保险机构能否解除保险参照的位移,在隔爆滑块下面,为悬臂卡锁式后坐保险机构设置有运动空间。仿真过程中采用的单位为kg-mm-ms-GPa。 意外跌落时,分别选取0.1 ms,15 000g以及0.15 ms,15 000g进行瞬态动力学仿真,得到悬臂卡锁的质量块与梁交叉点A处的位移随时间的变化趋势如图7所示,悬臂卡锁在0.1 ms,15 000g的位移小于在0.15 ms,15 000g的位移,验证了理论分析结论:意外跌落时,脉宽越大,悬臂卡锁响应位移越大。在0.15 ms,15 000g加速度作用下,悬臂卡锁应力云图和位移云图如图8(a)、(b)所示,悬臂卡锁的质量块与梁交叉点A处的最大位移为0.71 mm,小于隔爆滑块的厚度0.8 mm,隔爆滑块依然被卡住,此时最大应力出现在悬臂卡锁的固定端,为0.55 GPa,小于电铸镍材料的屈服强度0.75 GPa,在意外跌落加速度消失之后,悬臂卡锁在弹性力作用下回复到初始位置,卡住隔爆滑块。因此,悬臂卡锁式后坐保险机构在意外跌落时能够保证引信第一道保险处于安全状态。 正常发射时,分别选取4 ms,12 000g以及6 ms,12 000g两种加速度进行仿真,仿真时间设置为8 ms,便于观察加速度消失后的位移情况,得到悬臂卡锁的质量块与梁交叉点A处的位移随时间变化趋势如图9所示,悬臂卡锁在运动到触碰底板时达到其最大位移,在达到其最大位移之前,悬臂卡锁在6 ms,12 000g的位移小于4 ms,12 000g的位移,验证了理论分析结论:正常发射时,脉宽越大,悬臂卡锁位移越小。开始运动时,悬臂卡锁随着位移的增大应力也逐渐增大,在达到其屈服强度后,悬臂卡锁进入塑性变形阶段。在4 ms,12 000g加速度条件下,悬臂卡锁靠近固定端处B点的等效塑性应变随时间的变化趋势如图10所示,从图中看出,悬臂卡锁在0.4 ms后进入塑性变形阶段,在加速度消失后,悬臂卡锁不能回复到初始位置,其在8 ms时的位移云图如图11所示。在6 ms,12 000g加速度条件下,悬臂卡锁靠近固定端处B点的等效塑性应变随时间的变化趋势如图12所示,从图中看出,悬臂卡锁在0.6 ms后进入塑性变形阶段,在加速度消失后,悬臂卡锁不能回复到初始位置,其在8 ms时的位移云图如图13所示。从图10、图12中可以看出,正常发射时,无论在4 ms,12 000g加速度条件下还是6 ms,12 000g加速度条件下,悬臂卡锁等效塑性应变在0.6 ms后总是大于零,悬臂卡锁发生塑性变形,从图9、图11、图13可以看出,在载荷消失后,悬臂卡锁的位移均大于1 mm,且无法回复到初始位置,故可以保证正常发射时,引信第一道保险的可靠解除。 本文提出了可用于垂直于弹轴放置的MEMS安全系统的悬臂卡锁式后坐保险机构。该机构通过模型简化、理论分析得出其满足要求的固有角频率范围,根据满足要求的固有角频率建立仿真模型,通过仿真验证其可行性。仿真结果表明,悬臂卡锁式后坐保险机构可以实现对两种加速度环境的区分,意外跌落时,悬臂卡锁无法脱离隔爆滑块;正常发射时,悬臂卡锁脱离隔爆滑块并且通过其塑性变形达到定位的作用,从而保证安全系统在正常发射时第一道保险的可靠解除。 [1]徐泰然. MEMS和微系统设计与制造[M].北京: 机械工业出版社, 2004. [2]陈勇华. 微机电系统的研究与展望[J].电子机械工程, 2011,27(3):1-7. [3]谷雨. MEMS技术现状与发展前景[J]. 电子工业专用设备, 2013(8):1-8. [4]邓鹏, 吴玉斌, 郝永平. MEMS万向开关加工误差分析[J]. 兵器装备工程学报, 2016, 37(10):110-113. [5]王辅辅, 娄文忠, 王大奎,等. 一种用于旋转弹药的MEMS离心保险机构及其保险方法: 中国,CN104613828A[P]. 2015. [6]Fan L, Last H, Wood R, et al. SLIGA Based underwater weapon safety and arming system[J]. Microsystem Technologies, 1998, 4(4):168-171. [7]Robinson C H, Wood R H, Hoang T Q. Miniature MEMS-based electro-mechanical safety and arming device: US, US6964231[P]. 2005. [8]牛兰杰, 张建, 赵旭. 基于有限元法的MEMS后坐保险机构运动特性研究[J]. 探测与控制学报, 2006, 28(4):15-18. [9]程玄玄, 聂伟荣, 李艳桥,等. 引信MEMS保险机构剪断式后坐卡销[J]. 弹箭与制导学报, 2011, 31(6):102-104. [10]刘加凯, 齐杏林. MEMS安全系统的解除保险方式[J]. 探测与控制学报, 2012, 34(6):21-25. [11]Robinson C H, Wood R H, Gelak M R, et al. Ultra-miniature electro-mechanical safety and arming device: US, US 8276515 B1[P]. 2012. [12]蔡豪刚. 单轴敏感MEMS惯性开关的优化设计和制作[D]. 上海:上海交通大学, 2009. [13]郑利兵, 石庚辰, 韩立,等. 基于LIGA工艺的电铸镍材料特性[J]. 功能材料与器件学报, 2010, 16(3):222-226. [14]钱建刚, 李彭瑞, 李海婷. 溶液组分对电铸镍组织和力学性能的影响[J]. 航空材料学报, 2014, 34(2):11-16.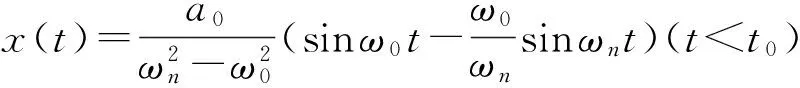
3 仿真分析

4 结论
