高g值冲击下变截面填充壳缓冲性能优化方法

徐 鹏，赵玉杰，朱江涛

(中北大学理学院，山西 太原 030051)

0 引言

在硬目标动能侵彻实验中，弹载测控电路通常承受着很高的加速度过载[1]。为了保证正常获取测量数据，需要对电路进行冲击隔离[2-5](如图1所示)。

目前，应用较为广泛的缓冲元件主要是薄壁金属构件。薄壁金属构件具有良好的吸能特性，在受到撞击载荷的作用时，破坏形式较为稳定，主要通过自身的塑性变形吸收和耗散能量，达到缓冲保护的目的[6]。此外泡沫铝作为一种新型的工程结构材料，具有密度小、塑性变形能力大、韧性高、机械性能好和价格低廉等优点，将其填充到金属薄壁管中，不仅可以提高空壳结构的刚度和吸能能力，而且可以改善空心壳变形模式的稳定性，因此形成一种很好的缓冲吸能结构，在汽车被动安全、航天器的回收等领域有着广阔的应用前景[7]。

近些年来，国内外学者对泡沫铝填充结构进行了大量的研究，Abramowitz、Reid等人对泡沫铝填充后的圆形截面和方形截面的薄壁铝管进行了大量试验研究，得出了泡沫材料的屈服应力即平台应力与泡沫材料相对密度之间的关系，并对泡沫材料的吸能特性进行了试验研究[8-9]；Hansson等人对所得试验数据进行了归纳、总结，并得出了用泡沫平台应力、薄壁管的直径、管壁厚和管壁材料的强度应力准确表示的平均压溃力的经验公式[10-11]。为了进一步设计性能更好的缓冲结构，很多学者提出优化方法对填充结构进行优化设计，如文献[12]分别以最小碰撞力、最大比吸能为目标，对泡沫铝密度和薄壁厚度进行优化设计。需要进一步考虑到不同目标对优化结果的影响程度及多个目标同时达到最优值来进行多目标优化，因此本文提出高g值冲击下泡沫铝填充变截面壳吸收能量最大化及测控电路承受加速度幅值最小化的多目标优化方法。

1 多目标优化方法理论基础

本文在对填充结构抗冲击性能进行优化设计时，采用了试验设计技术、代理模型近似求解技术和结构优化算法等理论与方法[13-15](如图2所示)。下面主要介绍全因子试验设计、响应面法以及目标规划法。

1.1 全因子试验设计

在一次试验中，系统的所有因素的所有水平的所有组合都需要被考虑的试验设计方法，它将每个因素的不同水平组合起来均作一次试验。在一项试验中若有n个因素，每个因素对应的水平数分别为l1,l2,…,ln,则全面试验的试验次数A为：

A=l1×l2×…×ln

(1)

当因素的个数不多，每个因素的水平也不多时，人们常用全面试验设计的方法，并且通过数据分析可以获取较丰富的结果，结论也比较准确。

1.2 响应面法

响应面法(RSM)[16]是试验设计与数理统计相结合用于建立经验模型的优化方法，基本思想是在试验测量、数值分析或经验公式的基础上，对设计空间内的设计点进行试验求值，从而构造测定量的全局逼近。

(2)

通过在设计空间中选取M(M>N)个设计样本点x(i)(i=1,2,…,M)进行显示有限元分析，进而得到向量y=[y(1),y(2)…,y(M)]T,并通过最小二乘法确定式(2)中的系数a=[a1,a2,…aN]T，则得系数a的表达式为：

a=(φTφ)-1(φTy)

(3)

式中，y=[y(1),y(2),…,y(M)]为有限元分析所得的响应向量；φ矩阵由M(M>N)个设计点处的基函数所组成，其表达式为

(4)

以两变量四次完全多项式基函数为例。则式(4)可以写成如下的完全展开式，即

(5)

把矩阵φ的具体形式和向量y=(y(1),y(2)…,y(M))T的具体数值代入式(4)中就求出了系数a的具体数值。进而求出了近似函数的表达式。

1.3 目标规划法

目标规划法又称为理想点法，其基本思想是通过构造统一目标函数使多目标优化方法转化为单目标优化方法，再对其进行求解使各个分目标尽可能逼近各自的理想最优值。本文采用平方加权和来构造目标规划法的统一目标函数，其表达式可以写成：

(6)

晟图机械是一家自1998年起就开始潜心研制、开发适用于精装印后装订，以及精品礼品盒包装皮壳科技的民营企业，伴随着中国改革开放的浪潮，晟图机械目前已经成为这一领域领先的民族品牌，而其背后成功的秘诀、一路走来的感悟，就这样在庹明珠的款款道来中徐徐展开……

(7)

2 有限元模拟

2.1 有限元模型

将图1所示加速度测试装置进行简化，以铝壳厚度和泡沫铝相对密度为设计变量，其中0.6 mm≤t1≤1.0 mm,t2=t1+0.2,t3=t1+0.5，0.23≤ρ′≤0.31(如图3所示)。采用全因子试验设计在设计区域内选取25个试验点，利用LS-DYNA仿真模拟获取相应的冲击信息，以冲击过程中泡沫铝填充变截面壳吸收能量最大化及测控电路承受加速度幅值最小化为优化指标，引入响应面法构造近似目标函数，最后通过目标规划法获得最优解。其中弹体外壳和测控电路采用质量等效方法简化成质量块，弹体外壳记为M1,质量为1 000 g,几何尺寸L×W×H为60 mm×60 mm×36 mm，测控电路记为M2,质量为280 g，几何尺寸L×W×H为60 mm×60 mm×10 mm，其中L、W、H分别为长方体的长宽高(如图4所示)。对外壳施加幅值80 000g脉宽120 μs的半正弦冲击加速度，如图5所示。

M1、M2均采用SOLD164单元，材料属性分别为弹性体、刚体,材料参数均为：密度ρ=7 800 kg/m3，弹性模量E=200 GPa，泊松比=0.3。金属壳采用SHELL单元，沿厚度方向有5个积分点，材料属性为塑性随动硬化模型。塑性随动强化模型就是在Cowper-Symonds关系式基础上建立起来的。其表达式如(8)：

(8)

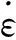
ρ/(kg/m3)E/GPanσy/MPaEt/MPaβC1P铝壳270068.60.3160110503342.71.972

2.2 LS-DYNA模拟结果

在0.6 mm≤t1≤1.0 mm，0.23≤ρ′≤0.31选取25个点进行模拟。测控电路承受的加速度幅值与填充结构吸能幅值如表2所示。

表2 模拟结果

3 填充结构缓冲性能优化方法的描述

3.1 测控电路承受加速度幅值最小化

在炮弹高速侵彻硬目标过程中，为了对弹载测试电路进行缓冲保护，要求传递到测控电路上的加速度值必须小于其所能承受最大值。因此测控电路承受加速度幅值A是描述结构抗冲击性能的一个重要指标。该优化方法的数学表达式为：

(9)

3.2 填充结构吸收能量最大化

结构吸收总能量EA是描述结构抗冲击性能的又一个重要指标，该优化方法的数学表达式为：

(10)

4 优化结果

4.1 求近似目标函数

选取四阶响应面近似模型，对铝壳厚度t1和泡沫铝密度ρ′进行优化，将表2中的数据代入式(3)中求得系数a,进而求得测控电路承受的加速度幅值函数y1(t1, ρ′)与填充结构吸能函数y2(t1, ρ′)。

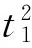
(11)

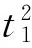
(12)

利用MATLAB作出目标函数的响应面及等高线如图7所示。

从图7可以明显看出加速度幅值随着厚度的增加先减小后增加，吸能幅值随密度的增加先减小再增大后再减小，所以在设计区域内必存在最优解。

为了测定响应面近似解与有限元的误差，定义了相对误差的表达式，即

(13)

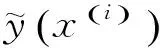
将25个试验点分别代入式(11)、式(12)中求得相应的加速度幅值与吸能幅值。代入式(13)中求出相对误差，如图8所示。

4.2 多目标优化

通过Matlab程序中的优化函数求得加速度幅值最优解为(0.811 4,0.247 5)，此时的加速度幅值为169 380 m/s2，吸能幅值为486.291 6 J；吸能幅值最优解为(0.695 8，0.298 9),此时的吸能幅值为495.218 0 J，加速度幅值为183 230 m/s2。

将多目标优化方法转化为单目标优化方法，取权系数w1=0.6,w2=0.4。代入式(6)中得：

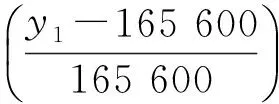
(14)

通过Matlab程序中的函数fmincon求得全局最优解为(0.789 9,0.257 5)，此时加速度幅值为170 080 m/s2,吸能幅值为487.388 3 J。相比加速度幅值最优解，吸能幅值提升了1.096 7 J；相比吸能幅值最优解，加速度幅值降低了13 150 m/s2。

A、EA各自最优解所组成的向量y′=(169 380,495.218 0)，全局最优解对应的目标值组成的向量y″=(170 080,487.388 3)。定义“./”为向量按位相除，通过向量(y″ -y′)./y′的2范数来判断优化结果的准确性，数值越小表明优化结果越准确。

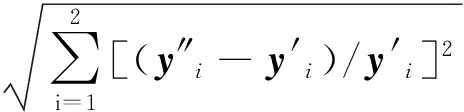
(15)

由式(15)得R=0.016 3,因此多目标优化结果比较理想。

5 结论

本文提出了高g值冲击下变截面填充壳缓冲性能优化方法，该方法同时满足测控电路所承受加速度幅值最小化和填充结构吸能最大化。以铝壳厚度和泡沫铝密度为设计变量，在0.6 mm≤t1≤1.0 mm, 0.23≤ρ′≤0.31范围内，通过全因子试验设计选取25个试验点，同时利用LS-DYNA获取相应的冲击信息，引入响应面法构造四阶近似目标函数，最后通过目标规划法获得最优解为(0.789 9,0.257 5)，此时加速度幅值为170 080 m/s2，吸能幅值为487.388 3 J。最后将向量(y″ -y′)./y′的2范数作为评价优化结果准确性的一个衡量因子，可以看出目标规划法得到的优化结果是比较准确的。此外，相比单目标优化结果，多目标优化综合考虑了评价结构抗冲击性能的多个重要指标，在一定载荷作用下对于选取更优的缓冲结构具有重要指导意义。

[1]徐鹏，锦彪，祖静，等.高g值冲击下存储测试电路模块缓冲保护研究[J].实验力学，2005，20(4)：610-614.

[2]徐鹏，祖静，范锦彪，等.高速动能弹侵彻硬目标加速度测试技术研究[J].振动与冲击，2007，26(11)：118-122.

[3]ZHANG W D, CHEN L J, XIONG J, et al. Ultra-high g deceleration-time measurement for the penetration into steel target[J]. International Journal of Impact Engineering, 2007, 34(3): 436-447.

[4]徐鹏，朱江涛，高猛，等.高g值冲击下泡沫铝填充铝壳轴压特性[J].探测与控制学报，2016，38(4)：77-82.

[5]高猛，徐鹏.高g值冲击下泡沫铝填充铝壳吸能特性研究[J].工程设计学报，2015，22(5)：469-475.

[6]孟卓，孙秦.不同轴截面薄壁筒在轴向冲击下吸能特性研究[J].计算机仿真，2010，27(8)：325-329.

[7]侯淑娟.薄壁构件的抗撞性优化设计[D].长沙：湖南大学力学与航空学院，2007：6-9.

[8]ABRAMOWITZ W, JONES N. Dynamic axial crushing of circular tubes[J]. International Journal of Impact Engineering, 1984, 2(3): 26-281.

[9]REID S R, REDDY T Y, GRAY M D, et al. Static and dynamic crushing of foam-filled sheet metal tubes[J]. International Journal of Mechanical Sciences, 1986, 28(5): 295-322.

[10] HANSSON A G, LANGSETH M, HOPPERSTAD O S, et al. Static crushing of square aluminium extrusions with aluminium foam filler[J]. International Journal of Mechanical Sciences, 1999, 41(8): 967-993.

[11] HANSSEN A G, LANGSETH M, HOPPERSTAD O S, et al. Static and dynamic crushing of square aluminium extrusions with aluminium foam filler[J]. International Journal of Impact Engineering, 2000, 24(4): 347-383.

[12] YIN H F, WEN G L, LIU Z B, et al. Crashworthiness optimization design for foam-filled multi-cell thin-walled structures[J]. Thin-Walled Structures, 2014, 75(2): 8-17.

[13]徐鹏，高猛.高g值冲击下泡沫铝填充壳结构抗冲击性能多目标优化[J].应用力学学报，2016，33(5)：845-852.

[14]高猛.高g值冲击下泡沫铝填充壳缓冲吸能多目标优化研究[D].太原：中北大学理学院，2016：10-16.

[15]董喜文.金属薄壁管的耐撞性优化设计[D].成都：西南交通大学力学与工程学院，2014：13-15.

[16] KHURI A I, MUKHOPADHYAY S. Response surface methodology[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2010, 2(2):128-149.

[17] 陈立周.机械优化设计方法[M].北京：冶金工业出版社，2005：43-47.

[18] 赵寿根，何著，杨嘉陵，等.几种航空铝材动态力学性能实验[J].北京航空航天大学学报，2007，33(8)：982-985.