基于FastICA的二次雷达混扰信号分选改进算法

李 丞，张 玉，唐 波

(国防科技大学电子对抗学院，安徽 合肥 230037)

0 引言

现代空中交通管制(ATC)常用的监控系统大多使用二次雷达作为探测系统。二次雷达可以通过发射询问信号、接收应答信号的方式获取飞机的距离方位、气压高度、飞机代码等飞行讯息[1]。现代二次雷达系统常用SIF模式与S模式作为信号组成内容。两种模式虽均以1 030 MHz与1 090 MHz为询问频率与应答频率，但在SIF模式上发展起来的S模式却因为其特有的信号结构与一定的复杂度和自我纠错能力逐步成为主要交通信号模式。随着空中交通流量的日益加大，电磁环境日益复杂，多种应答信号产生交互影响的情况越发严重，而这也影响了信号的模式种类识别与解码，降低了二次雷达系统的安全性与可靠性[2-3]。

针对日益严重的二次雷达信号混扰后分选问题，目前国内外公认的几种常用处理算法。例如：旋转不变因子技术(ESPRIT)能够较准确地估计出应答机信号到达方向(DOA)，分选性能较好，但要求阵列天线应精确校准[4]； N.Petrochilos提出了基于S模式信号编码特性的曼彻斯特解码算法(MDA)，虽然具有针对S模式信号非常好的分选性能，但此算法针对性太强，不能适用于其他类型信号格式，且运算量较大[5]；由P.Comon提出的独立成分分析(ICA)算法以及后由Hyvarinen等人提出的固定点算法(FastICA)应用于二次雷达信号分选问题虽具有很高鲁棒性，但其算法存在分选时间较长、计算量较大、分选性能不佳等问题[6-7]。本文针对上述问题，提出了基于FastICA的二次雷达混扰信号分选改进算法。

1 FastICA算法简介

1.1 混扰信号分选模型

现代二次雷达系统中，大多采用阵列天线对空中信号采集，故本文以阵列信号为例分析。

在阵列信号中常被观测到的混扰矩阵Y可表示为：

Y=AS+N

(1)

式中：Y=[y1,y2,…,yM]T∈M×N为混扰信号矩阵；A=[a1,a2,…,aK]∈M×K为引导矩阵；S=[s1,s2,…,sK]T∈K×N为应答信号矩阵；N=[n1,n2,…,nM]T∈M×N为噪声矩阵。

二次雷达系统混扰信号分选问题的实质是：在若干应答信号矩阵S与引导矩阵A均未知的情况下，利用已知的混扰信号矩阵Y特性确定一解混矩阵W，利用WY对S进行估计。在没有噪声的情况下，分选问题较为简单。然而，在含噪条件下，混扰信号分选的问题相对复杂。因为WY=WAS+WN≈S+WN，是应答信号与噪声的叠加，则即使使用无噪条件下的解混矩阵最优解进行解混，分选效果仍旧不佳。故，含噪条件下解混矩阵W的最佳估计为信号分选问题解决的关键。

1.2 FastICA算法简介

FastICA算法又称固定点算法，是一种快速寻优迭代算法。该算法采用批处理的方式，在每一步迭代中都有大量样本数据参与运算。在通过预处理去除数据的相关性之后，根据中心极限定理，若干个独立随机变量的线性和将趋向于高斯分布，则算法通过衡量最大非高斯性达到分离目的。

鉴于信号特性中的零恒模特性以及复信号特性，传统FastICA算法并不能实现对S模式信号的有效分选，但由Mike等人提出的NC-FastICA算法对于该模式信号分选性能较好[8-9]，故引用此算法为改进基础。在使用此算法之前，需对混扰信号矩阵Y做白化处理后可得白化后的混扰信号矩阵Z为

Z=TY

(2)

其中，矩阵Z的各行互不相关，即：

RZZ=E[ZZH]=I

(3)

预处理后，取wk为分离矩阵W的第k列。则ICA的权值可通过如下优化问题求解

(4)

其中，G为权值函数。

利用拉格朗日乘子法，可将式(4)的优化问题写为

E{g(|wHZ|2)ZZHw}-λw=0

(5)

以牛顿法来求解上式问题，在第(n+1)次迭代中

(6)

式中，w(n)表示第n次迭代的权值；Hw的表达式为

(7)

近似后可将Hw写为

Hw=E{g(|wHZ|2)+g′(|wHZ|2)|wHZ|2-λ}I

(8)

则牛顿迭代过程可以写成

(9)

归一化之后为

(10)

通常在估计多个独立成分时，FastICA算法有两种处理方式: 一种是渐进正交化，即串行方式; 另一种是对称正交化，即并行方式。由于串行方式具有以下缺点: 先估计出的向量误差会累积到后面的向量估计中，这主要是由于正交化过程造成的。此外，采用对称正交化方法时，每个分量的地位是均等的，并且可以同时估计出所有独立分量，因此在这里采用对称正交化方法。

2 FastICA算法的改进

2.1 分离矩阵初值估计

通过之前有关ICA与FastICA算法的简介不难发现，尽管FastICA算法针对步长调节等人为参数进行改进，但其迭代起始矩阵的选取仍然是以单位矩阵进行迭代，则其算法在存在噪声时分选性能有所降低并在高噪声时易出现分离失败。故此本文针对其起始矩阵的选定进行改进，改进算法如下。

假设两个模式S应答信号几乎同时被接收，两信号在时间上重叠如图1所示，可见在t1到t2时间段内只存在信号s1，在t2到t3时间段内信号s1与s2重叠，在t3到t4时间段内只存在信号s2。

如图所示，不难发现时间段(t1,t2)与(t3,t4)分别为先后两个信号的开始点与结束点，不妨将整段信号分为三部分：[t1:t2]段仅含有s1信号，[t2:t3]段同时具有两个信号，[t3:t4]段仅含有s2信号。

以上仅为信号结构的介绍，在实际PA算法中，算法的第一步就是进行四个时间节点的检测，具体方法采用奇异值分解法，即通过奇异值分解取得某些时间段内较大的奇异值，通过与预设噪声门限的比对，确定奇异点个数，以确定可能的信号数。通常，在奇异值分解法中，采样率取50 MHz，将X分为每4 μs一小段即200个采样点，对每段信号进行奇异值分解，各段奇异值如图2所示。可以看出，在t1到t2时间段内存在一个较大奇异值，则此段时间内只存在信号s1；在t2到t3时间段内存在两个较大奇异值，则在此时间段内发生了信号的交叠；在t3到t4时间段内存在一个较大奇异值，则此段时间内只存在信号s2。由此可见，通过奇异值分解可以估计出未发生交叠的时间段和发生交叠的时间段。

X(1)=MS(1)+N(1)
X(2)=MS(2)+N(2)

(11)

式中：S(1)和S(2)分别为信号S在[t1:t2]和[t3:t4]时间段内的子集。X(1)只包含信号s1的信息，同样X(2)只包含信号s2的信息，则式(11)可简化为

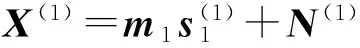
(12)

式中：m1和m2为A的列向量；s1和s2为S的行向量。

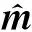
(13)

2.2 投影改进FastICA算法分选流程

投影改进FastICA算法分选流程如下：

第二步：1)：通过MDL算法估计应答机个数K；

2)：对混扰信号矩阵Y做预处理得到矩阵Z=TY，并设取k=1；

3)：取分离矩阵W的列矢量wk；

4)：计算Q=WHZ并更新权值；

5)：k←k+1，若k

6)：进行正交化，公式如下：

W←(WWH)1/2W

7)：判断W是否收敛，若未收敛，重新令k=1，并返回第三步，此处判断收敛条件可取前后两次更新误差；

3 仿真分析

3.1 仿真实验

以2个模式S应答信号发生混扰的情况为例，现假设天线阵元数为M=4，以50 MHz的采样率对下变频后的信号进行数字采样， 在两个固定信号的DOA值分别为-3°和5°，相对延时为30 μs，信噪比为20 dB。图1为噪声环境下两个S模式应答信号发生混扰的情形，可见两个信号在时域上重叠，如果直接对其解码会造成大量误码。图3，图4为本文算法分选得到的两个应答信号，可见本算法可成功地分离出发生混扰的两个信号，并且算法分选得到的信号幅值稳定，几乎无噪声干扰，可以直接对其进行解码。

如上图所示，本文提出的算法应用在两个模式S信号混扰时具有较好的分离性能。那么，针对于模式S具有相似性质的SIF模式的混扰情况分选情况不再赘述。

3.2 性能分析

分选算法效果主要受信噪比、天线是否精确校正、发生混扰的应答信号样式等因素影响，因此需要分别考虑各因素在分选中的影响状况。本文算法为盲分选算法，即引导矩阵A结构未知的情况下，对信号进行分选，因此不要求天线精确校正，且需要将天线耦合、阵列扰动等因素考虑在内。

以分离指数I作为分选性能评价指标

(14)

式中，I∈[0,1]；令E=10lgI，则有E≤0，且E值越小算法分选性能越好；令P=WA，pij为全局矩阵P的第i行第j列元素；W为分离矩阵，A为引导矩阵。仿真结果均取1 000次独立蒙特卡罗实验的平均值[9]。

图5为SIF模式信号混扰情形下的本文算法分离指数曲线。通过曲线可清晰地发现，本文算法分离指数始终小于PA算法与FastICA算法，并且具有明显提升，说明本文算法的分选性能较好。此外，尽管在信噪比较低时，三种算法分选性能没有明显区别，但是随着信噪比逐渐升高，本文算法性能优势逐渐体现出来，相较另两种算法性能提升明显。

图6为SIF模式信号混扰情形下的本文算法分选误码率分析。整体来看，由于SIF模式混扰信号构成以及信号格式相对简单，三种算法分选得到的应答信号误码率均较低。当信噪比大于9 dB后的误码率均低于5%；当信噪比大于12 dB后，除FastICA算法误码率稳定在4%左右外，PA算法与本文改进算法的误码率几乎为零，可见本文算法分选性能较优。

考虑两个S模式应答信号发生混扰的情形时，两个固定信号的DOA值分别为-3°和5°，相对延时为30 μs，信噪比为20 dB，其他条件不变。

图7为S模式信号混扰情形下的本文算法分离指数曲线。通过对比发现，随着信噪比的增加，FastICA算法尽管相较ICA算法有所改进，但仍不具有优秀的分选性能。其原因是S模式应答信号的峭度值近似为零，表现出较强的高斯性，当多个S模式应答信号混扰时，高斯性比较复杂，FastICA算法复杂度不足，无法有效分选。本文算法同PA算法一致，依然单调减小，表现出极好的分选性能。由此可见，本文算法鲁棒性较好，对混扰信号格式要求较低。

图8为S模式信号混扰情形下的本文算法分选误码率分析。对比发现，三种算法对S模式混扰信号进行分选时的误码率，高于对SIF模式混扰信号进行分选时的误码率，是因为S模式应答信号脉冲串较长，信号中码字较多，误码易发生。FastICA算法的误码率始终在20%以上，性能一般；PA算法性能则跟随信噪比逐渐升高而误码率降低；本文算法则在信噪比大于10 dB后，误码率低于10%，且信噪比大于15 dB后，误码率趋近于零，可见其分选性能优异。

如表1所示，虽然本文算法相较FastICA算法与PA算法在信号分离精度上有了很大的提升，但由于算法结构相对复杂，计算时间变得更长，即算法在提升分离精度同时牺牲了计算速度。因此，本文算法存在着速度相对较慢的缺点，这一点需要改进。

表1 计算时间比较

4 结论

本文提出了基于FastICA的二次雷达混扰信号分选改进算法。该算法首先利用投影算法(PA)对权值矩阵W进行初步估计；进而通过负熵的度量进行迭代寻求最佳解，求解得出分离矩阵；最后利用分离矩阵实现对混扰信号有效分选。仿真验证表明，该改进算法在复杂环境下有效进行模式信号分选，且其性能在相较同类算法时具有更好的抗噪性能与分选性能。但本文算法由于结构相对复杂，计算时间变得更长，即算法在提升分离精度同时牺牲了计算速度，且同FsatICA算法一样，算法是针对信号的高斯性差异进行分选，故针对多种类型信号混扰时，性能仍有待提高，此问题有待下一步研究。

[1]张尉. 二次雷达原理[M]. 北京: 国防工业出版社，2009: 9-12.

[2]王洪, 刘昌忠, 汪学刚. 二次雷达 S 模式综述[J]. 电讯技术, 2008, 48(7): 113-118.

[3]刘垒，张玉，唐波.基于曼彻斯特编码特性的二次雷达混扰信号分选[J].探测与控制学报，2017，39(1)：20-25.

[4]唐波, 程水英, 张浩. 基于多通道阵列处理的二次雷达混扰信号分选[J]. 电讯技术, 2014, 54(5): 534-540.

[5]Petrochilos N, Piracci E G, Galati G. Improved MDA, a case for de-garbling SSR mode S replies[C]//IEEE Tyrrhenian International Workshop on Digital Communications-Enhanced Surveillance of Aircraft and Vehicles (TIWDC/ESAV), Roma, 2014: 87-91.

[6]Chaumette E, Comon P, Muller D. ICA-based technique for radiating sources estimation: application to airport surveillance[J]. IEE Proc-F, 1993, 140(6):395-401.

[7]张玉, 樊斌斌, 胡进, 等. 基于最小残量优化算法的二次雷达信号分选[J]. 现代雷达, 2015, 37(4): 46-49，54.

[8]Galati G,Petrochilos N, Piracci E G. Degarbling Mode S replies received in single channel stations with a digital incremental improvement[J]. IET Radar, Sonar &, Navigation, 2015, 9(6): 681-691.

[9]刘垒，张玉，胡进，等. 基于改进投影算法的二次雷达混扰信号分[J]. 现代雷达，2016， 38(6): 22-26.