两点磁梯度张量定位方法
2018-03-12戴忠华周穗华
戴忠华,周穗华,单 珊
(海军工程大学兵器工程系,湖北 武汉 430033)
0 引言
铁磁体在地球磁场的磁化作用下,会在其周围产生一个附加磁场,该磁场常常作为磁性目标探测、定位和识别的信号源[1-3]。磁性目标定位技术在航空磁探、航空反潜以及水中兵器中运用广泛,与磁测量技术的发展息息相关。目前,磁测量技术主要有磁场总量测量、磁场分量测量和磁梯度张量测量,相应的基于磁测量信息的定位方法也有磁场标量定位方法、磁场矢量定位方法和磁梯度张量定位方法。在实际运用中,将磁性目标等效为磁偶极子或者混合模型,基于标量或者矢量的传统定位方法一般利用大量的测量数据根据模型建立非线性方程,然后利用各种优化算法进行求解,这种方法计算量大且实时性差[4-6]。基于磁梯度张量的定位方法在国外早就被提出[7-11],由于其具有定位速度快、定位精度高的特点,近几年在国内已成为磁性目标定位的研究热点,相继有许多相关的定位方法被提出来。
文献[10-11]中初步探讨了利用磁梯度张量进行定位,利用单点的磁梯度张量进行定位,分析了影响定位效果的因素,但受地磁影响较大,并且定位存在多解性。为了减小地磁干扰的影响,文献[12-16]中分别利用多点磁梯度张量差分计算、梯度张量变化率计算、滤波算法来改进单点磁梯度张量算法。文献[17-18]中对解唯一性进行研究,并提出基于梯度张量矩阵本身的特征值和特征向量的定位方法。综上所述,基于磁梯度张量的定位方法需要解决地磁干扰与定位多解性两个问题。本文针对上述问题,提出了两点磁梯度张量定位方法。
1 磁梯度张量定位原理
1.1 磁梯度张量
在进行磁性目标磁场测量时,通常用矢量磁力仪测磁场强度的三个分量B=(Bx,By,Bz)。现对该三分量进行一次梯度运算,即可得到它的磁梯度张量,如下:
G=
(1)
式中,G为磁梯度张量,共包括9个要素,它描述了目标磁场各分量在空间三方向上的变化率。
目标磁场可以看作是静磁场,由于没有电流存在,无源空间中的磁场具有无旋性和无散性,即:
divB=
(2)
rotH=
(3)
联立式(2)、式(3)可得:
(4)
因此式(1)中的磁梯度张量矩阵G简化为只有5个独立要素,且为对称矩阵。
1.2 磁梯度张量定位原理
当测量系统与磁性目标之间的距离大于2.5倍目标尺度时,磁性目标可以等效为单磁偶极子,在距离磁偶极子r处的磁场强度为
(5)
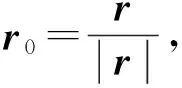
(6)
因此,可得:
(7)
又
B′-B=Gr0dr
(8)
所以,由式(7)、式(8)得:
(9)
r=-3G-1B
(10)
式(10)为单点的磁梯度定位算法,已知单一观测量点的磁场强度和磁梯度张量可实现磁性目标定位。
从定位方程(10)中可知,单点定位不仅与该点的磁梯度张量大小有关,也与该点所测量得到的磁场测量值有关。在实际测量中,测量得到的磁场测量值中不仅只有目标磁场,还包括了地球磁场。地球磁场的梯度值相对来说比较小,一般小于0.02 nT/m,所以在地磁场环境中对磁性目标梯度张量的测量可以用测量系统的实际测量值近似代替;而由于地球磁场通常达到几万纳特,若测量系统距离目标较远时,目标磁场完全淹没在地磁场中,目标磁场测量值并不能用实际磁场测量值代替。如果不去除地球磁场,由式(10)所得的定位结果误差较大,因此,单点磁梯度张量定位方法不能忽略地球磁场的影响。
2 两点磁梯度张量定位方法
2.1 两点定位原理
为了减少地磁场的影响,本文利用两点磁梯度张量来进行定位。假设测量系统的速度v=(vx,vy,vz)和采样频率Ts已知,测量系统连续两点的磁梯度张量为G1、G2。由式(10)可得
G1r1=-3B1
(11)
G2r2=-3B2
(12)
其中,r2=r1+TsvT。
又F1M=B1,F2M=B2。因此由式(11)、式(12)可得:
G2r2=F2F1-1G1r1
(13)
其中,G1、G2为两点的梯度张量;r1、r2分别为第一个点和第二个点的位置坐标,它们之间的关系为r2=r1+TsvT;F1和F2为两点由磁偶极子模型得到的系数矩阵,为r1=(x1,y1,z1)T的函数。假设测得连续两点的磁张量梯度,代入式(13),则式(13)为只与第一个点位置参数相关的非线性方程。若能精确解出方程的解,即能实现目标定位。
解式(13)的非线性方程,无法直接求得,可构造目标函数
f=min‖G2r2-F2F1-1G1r1‖2
(14)
对式(14)中的x1,y1,z1三个位置参数进行优化,得到目标函数最小值,此时对应的x1,y1,z1为式(13)的近似解,即完成对第一个点的定位。
从式(14)中可知,两点磁梯度定位方法只用了系数矩阵与两点的梯度张量测量值,并未直接利用测量系统所测的磁场测量值,在一定程度上减小了地磁的影响。
2.2 参数优化算法
由2.1节可知,两点磁梯度张量定位原理归结为非线性优化问题。为实现磁性目标的实时定位,因此优化算法应尽量简便,计算量小,但必须满足所求的解为全局最优。由于POWELL法在经典迭代算法中收敛速度较快,但是与初值的选择有关。因此本文将单点定位算法和POWELL算法结合起来。
先利用单点的磁梯度定位算法获得近似解,以此解作为POWELL算法的初始值,再利用POWELL算法进一步确定最优解,从而获得该点的定位。
2.3 磁梯度张量测量系统
根据本文提出的定位方法,设计如图1所示的平面三矢量磁力仪磁梯度测量系统,矢量磁力仪分布在两根垂直线上,以1号矢量磁力仪为原点建立空间直角坐标系,三个矢量磁力仪的三轴与坐标系三轴一致,两磁力仪之间的基线长度为d。
(15)
因全梯度张量是5个独立元素矩阵,因此可由式(4)得到其他量,从而获得1号磁力仪处的磁梯度张量。若此测量系统安装在运动平台上,运动平台的速度和测量系统的采样频率已知,则根据本文提出的两点磁梯度张量定位方法对磁性目标进行定位。
3 仿真分析
仿真实验需要完成工作:1)利用本文提出的定位方法对磁性目标进行定位仿真实验,检验在有地磁情况下,本文提出的方法定位磁性目标是否有效;2)比较该方法与原单点定位方法的定位效果;3)讨论影响定位精度的因素。在仿真实验中,将测量系统固定在运动平台上,磁性目标静止,载体平台从磁偶极子目标上方通过,以测量得的数据来进行磁性目标定位。如图2所示,磁性目标位于空间坐标原点,梯度张量测量系统的坐标轴平行空间坐标轴。
设磁性目标的磁矩参数为Mx=4×107Am2、My=1×106Am2、Mz=1×106Am2,测量平台从点(-200,50,100)开始沿平行于x轴运动,运动速度为(5,0,0)m/s,采样频率为1 Hz,假设测量地区的地磁为(-30 000,20 000,25 000)nT,测量系统的基线为0.5 m,磁力仪的精度为0.01 nT。仿真实验的步骤如下:
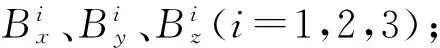
2)由式(15)计算得到测量系统1号矢量磁力仪的磁梯度张量矩阵;
3)将测量系统1号磁力仪的磁场加上地磁场,利用本文提出的方法和原有的单点定位方法进行定位;
4)分别计算本文提出方法与原单点定位方法的定位误差,分析两种方法的优劣。
3.1 现方法与原方法的比较
按照上述的仿真实验步骤,对磁性目标进行定位,计算结果如图3,图4所示。
从图3中可以看出,本文提出的方法定位效果比较好,在距离磁性目标200 m处,最大的定位误差为15 m;随着距离的减小磁性目标三个方向的定位误差也随之减小,在150 m定位范围内,本文提出的方法可以实现精确定位。
图4为在存在地磁时,现方法与原方法定位的误差。分析图4可知,在地磁环境中定位时,本文方法的定位效果很好,相对于原单点定位方法,不管是远距离还是近距离定位,本文方法明显优于原单点定位方法,在近距离定位时,误差仅为原方法的20%。
3.2 定位精度的影响因素
首先,将基线分别设置为0.25 m,0.5 m,1 m,其他初始条件不变,分别计算三种基线的定位误差。然后将磁力仪精度分别设置为0.001 nT,0.01 nT,0.1 nT,其他初始条件不变,分别计算各磁力仪精度的定位误差。计算结果如图5,图6所示。
从图5的计算结果可知,三种基线在距磁性目标较近时都有较好的定位效果,但是远距离对目标定位,基线的大小影响较大,且如果要远距离定位保持良好的定位效果,测量系统的基线应取的大一些。图6为不同磁力仪精度计算的定位误差,远距离定位时,磁力仪精度越高,定位误差越小;近距离定位时,磁力仪精度对定位效果影响不明显。从上面分析可知,远距离定位时,测量系统的基线大小和磁力仪精度对定位精度影响较大。
4 结论
本文提出了两点磁梯度张量定位方法。该方法基于单点磁张量梯度定位原理,利用运动载体测量系统的连续两点磁梯度张量,结合磁偶极子模型方程,构建两点磁梯度张量非线性目标函数,采用单点定位和POWELL混合优化算法对位置参数进行求解。仿真实验结果表明,在有地磁干扰的情况下,本文所提方法与原单点磁梯度定位方法相比受地磁影响小,定位精度较高,测量系统基线大小和磁力仪精度是影响远距离定位精度的主要因素。
[1]Tarek El Tobely,Ahmed Salem.Position detection of unexploded ordnance from airborne magnetic anomaly data U-sing 3-D self organized feature map[J]. International Symposium on Signal Processing and Information Technology , 2005,23(1):322-327.
[2]张昌达.航空磁力梯度张量测量——航空磁测技术的最新进展[J].工程地球物理学报,2006,3(5):354-361.
[3]Hirota M,Furuse T,Ebana K .Magnetic detection of a surface ship by an airborne LTS SQUID MAD[J]. Applied Superconductivity, IEEE Transactions on Magnetics,2001,11(1):884-887.
[4]Xiao Changhan,Liu Shengdao,Zhou Guohua.Real-time localization of a magnetic object with total field data[M].US:IEEE, 2008.
[5]林春生.舰船磁场信号检测与磁性目标定位[D].武汉:海军工程学院,1996.
[6]隗燕琳,肖昌汉,陈敬超,等.基于舰船矢量磁场的定位方法[J].上海交通大学学报,2009,43(8):1216-1220.
[7]Wynn W M.Dipole tracking with a gradiometer[J]. Naval Ship Research and Development Laboratory Informal Report NSRDL/PC ,1972: 3493.
[8]Charles P Frahm.Inversion of the magnetic field gradient equations for a magnetic dipole field[J]. NCSL Informal Report ,1972: 135-72.
[9]Wynn W M,Frahm C P, Carroll P J. Advanced superconducting gradiometer/magnetometer arrays and a novel signal processing technioque[J].IEEE Transactions on Magnetics , 1975,11(2):701-707.
[10] Wynn W M. Magnetic dipole localization with a gradiometer:obtaining unique solutions[J]. IEEE International , 1997(4): 1483-1485.
[11]Nara T,Suzuki S,Ando S. A closed-form formula for magnetic dipole localization by measurement of its magnetic field and spatial gradients[J].IEEE Transactions on Magnetics, 2006,42(10):3291-3293.
[12]肖昌汉,何华辉.磁性物体探测的线性求解方法[J].华中理工大学学报,1997,25(4):83-85.
[13]张朝阳,肖昌汉,阎辉.磁性目标的单点磁梯度张量定位方法[J].探测与控制学报, 2009,31(4):44-48.
[14]李光,随阳轶,刘丽敏.基于差分的磁偶极子单点张量定位方法[J].探测与控制学报, 2012,34(5):50-54.
[15]于振涛,吕俊伟,樊利恒.基于磁梯度张量的目标定位改进方法[J].系统工程与电子技术, 2014,36(7):1250-1254.
[16]于振涛,吕俊伟,许素芹.运动平台的磁性目标实时定位方法[J].哈尔滨工程大学学报,2015(5):606-610.
[17]高俊吉,刘大明,周国华.水中非合作运动磁性目标跟踪及参数估计[J].哈尔滨工程大学学报,2013(9):1124-1130.
[19]吴招才.磁力梯度张量的偶极子定位方法[C]//中国地球物理学会:中国地球物理(2009).北京:中国地球物理学会,2009.
[18]万成彪,潘孟春,张琦.基于张量特征值和特征向量的磁性目标定位[J].吉林大学学报(工学版),2017,47(2):655-660.
