联合协方差矩阵重构与导向矢量校正的稳健波束形成方法
2018-03-12冯西安
鲁 欢,冯西安
(西北工业大学航海学院,陕西 西安 710072)
0 引言
稳健波束形成是阵列信号处理中的重要方向,在声呐、雷达、导航、通信、麦克风阵列语音处理以及地震勘测等科技领域中得到了极为广泛的应用。稳健波束形成的典型方法是Capon波束形成[1],它是建立在对期望信号导向矢量与干扰协方差矩阵准确已知的条件下。但实际应用中,存在两个重要的问题需要解决:一个是采样快拍中含有较强期望信号成分使得利用采样协方差矩阵波束形成器的性能在高信噪比情况下会急剧下降[2-4]。另一个是由于观测方向误差、幅相不一致、位置偏差等因素导致的期望信号导向矢量失配。为了使波束形成在强期望信号时具有较好的性能,已提出了许多稳健性方法。文献[5]将Capon空间谱估计在去除期望信号来波方向后的空域进行积分,得到重构的干扰加噪声协方差矩阵;但是其对角度失配误差仍然较为敏感,致使主波束无法对准期望信号,从而削弱了输出期望信号功率。文献[6]通过估计期望信号功率来重构干扰加噪声协方差矩阵,虽然具有良好的抗强期望信号背景的能力,但随着信噪比的变化,该方法在干扰信号方向不再置零,甚至变成了非自适应的方法。另外,为了改善方法对于导向矢量误差的敏感性,文献[7]采用了对角加载波束形成(Diagonal Loading Beamforming,DL),但如何确定最优加载量仍是一个难题。文献[8]采用了基于特征子空间(Eigen-Subspace Beamforming,ESB)的稳健波束形成,对导向矢量误差具有良好的鲁棒性,但其接收信号中必须包含较强期望信号且需要子空间维数的先验信息或估计。文献[9-11]将估计导向矢量的问题转换为一个凸优化问题来对导向矢量进行矫正,但此方法运算量大且不稳定,工程实现难。本文针对上述问题,提出了联合协方差矩阵重构与导向矢量校正的稳健波束形成方法。
1 问题描述
假设有Q+1个相互独立窄带信号入射到M元均匀线列阵,其中M>Q+1,入射信号与噪声相互独立,其中期望信号的导向矢量为a(θ0),干扰信号的导向矢量为a(θj),j=1,2,…,Q,那么阵列接收信号可表示为:
x(t)=As(t)+υ(t)
(1)
Capon波束形成基于以下最优问题:
(2)
其解为:
(3)
式中,Ri+n是干扰加噪声协方差矩阵。

(4)
实际中存在的多种误差使得估计导向矢量与真实导向矢量往往是不一致的,即存在失配量。信号估计导向矢量可以表示为:
(5)
(6)
可以看出,一方面当期望信号的功率很强的话,波束形成器会抑制期望信号。另一方面当估计的方位与实际来波方向有偏差时,波束形成器的主波束不能准确地指向期望信号方向。综合考虑这两个关键问题,本文提出一种联合协方差矩阵重构与导向矢量校正的方法来解决这些问题。
2 联合协方差矩阵重构与导向矢量校正的稳健波束形成
2.1 噪声加干扰的协方差矩阵重构
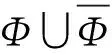
构造如下的不确定性集合:
(7)
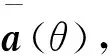
由Capon空间谱估计可知,波束形成器输出平均功率为:
(8)
考虑到干扰的实际导向矢量必须位于高维曲面环Sa(θ∈Φint)中,重建干扰协方差矩阵为:
(9)
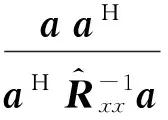
(10)
式中,∂Sa(θ∈Φint)代表Sa(θ∈Φint)高维曲面环的表面。这个积分通过收集更多的高维表面积分的潜在信息来解决这个问题。
然而,求解式(10)中的积分是很困难的。可以将上述式(10)近似为:
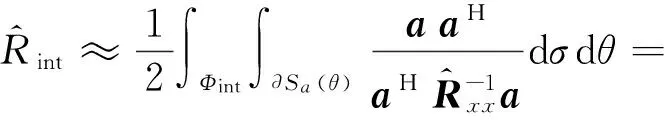
(11)
(12)
对于θi∈Φint,式(12)是面积分,它近似为
(13)
式中,L是∂Sa(θi)中的采样点数。ail∈∂Sa(θi)表示位于三维曲面环域上的导向矢量。
(14)
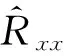
最后得到重构的干扰加噪声协方差矩阵为
(15)

(16)
此方法利用重构的干扰加噪声协方差矩阵,排除了期望信号分量对波束形成性能的影响。接下来,将进一步采用导向矢量校正来提高波束形成的性能。
2.2 导向矢量校正
由于期望信号的可能来波方向上的导向矢量可构成一个线性空间,那么对期望信号导向矢量的校正可表示为这一线性空间的基向量的线性组合。基于空间投影(SP,Space Projection)的Capon波束形成方法[12]就是利用这一方法对期望信号导向矢量进行校正,有效地提高期望信号导向矢量失配情况下波束形成的稳健性。
(17)
通过均匀划分空域区间Θ,再依次求和的方法,可得到正定矩阵Q表示为:
(18)

(19)
(20)
将式(19)代入式(20)得
(21)
(22)

(23)
(24)
由式(24)可知,最优权矢量既排除了期望信号分量对波束形成的影响,同时又重新估计了期望信号的导向矢量,降低了波束形成对导向矢量失配误差的敏感性,使得稳健性有了更大的提升。
2.3 方法流程
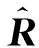
3)计算得到重构的干扰加噪声矩阵为
3 仿真结果
在仿真中,采用半波长间隔无指向性阵元数为M=10的均匀线阵列。期望信号为高斯随机信号,噪声为高斯白噪声。期望信号的实际方位角θ0=0°,干扰信号的实际方位角为θ1=-40°和θ2=60°。所有结果都是1 000次蒙特卡罗模拟的平均值。
最优波束形成是基于最大输出SINR准则得到的波束形成,是衡量波束形成方法性能的重要指标。将本文提出的方法与下述方法进行对比:标准Capon方法[1]、对角加载方法[7]、基于特征子空间投影方法[8]、矩阵重构方法[11]、导向矢量校正方法[12]。
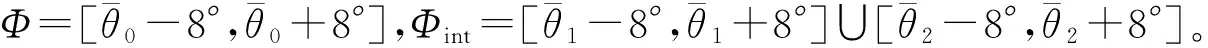
实验1:不同信噪比下的波束图
从图2(a)可以看出,当期望信号功率较小时,导向矢量校正和提出的方法经过导向矢量的校正,波束图形状都较为理想,能准确地指向期望信号来波方向,并在干扰信号的来波方向上形成零陷,具有优秀的抗干扰能力。对角加载方法和矩阵重构方法通过改进,在一定程度上校正了导向矢量;特征子空间投影方法通过投影的思想在一定程度上也校正了导向矢量,其主波束能较准确地指向期望信号的来波方向,并且在干扰处生成零陷;Capon波束形成由于失配误差的存在,主波束有些偏移,但在干扰处仍能生成较深的零陷。
从图2(b)可以看出,当期望信号比较大时,提出的方法对导向矢量进行了校正,又重构了协方差矩阵,所以这种方法对失配误差不敏感,具有理想的主波束指向性和干扰抑制能力。Capon方法已无法准确对准期望信号的来波方向,甚至在期望方向形成了零陷;对角加载方法的波束指向性虽然优于Capon方法,但是由于期望信号的增强,使得其在干扰信号方向的抑制能力减弱,丧失了抗干扰能力;特征子空间投影方法仍然具有较好的波束指向性,但由于信噪比太高,使得抑制干扰的能力减弱;矩阵重构方法基本不受输入信噪比的影响,同图2(a)中的基本相同;导向矢量校正方法虽然具有较好的指向性,但对干扰的抑制能力降低。因此提出的方法不仅存在导向矢量失配,而且在强期望信号背景下都有很理想的输出。
实验2:不同SNR下的输出SINR
从图3可以看出,矩阵重构和提出的方法由于使用了重构协方差矩阵将期望信号的影响给排除了,所以输出SINR十分接近最佳SINR,但由于提出的方法还对导向矢量进行了校正,所以其输出性能略优于矩阵重构方法。Capon方法在较小的SNR值时的输出SINR已经开始下降。对角加载方法因为其加载电平的存在,所以性能较优于Capon方法。特征子空间投影方法提高了其输出SINR及稳健性,但是随着SNR的增加,方法输出SINR逐渐趋于平稳。导向矢量校正的输出SINR随SNR的增加而增加,但因为只校正了导向矢量,没有排除期望信号的影响,所以随SNR的增大,方法输出SINR逐渐趋于平稳。
实验3:少快拍数下的输出SINR
从图4可以看出,本文提出的方法输出SINR是最接近最优的SINR的,并且除矩阵重构方法外其输出SINR的收敛速度是最快的。尽管矩阵重构方法输出SINR的收敛速度与本文所提方法相同,但是其输出SINR总是低于本文所提方法的输出SINR。特征子空间投影方法与导向矢量校正方法的输出SINR的收敛趋势比较接近,只是前者的输出SINR要高于后者。而Capon方法的性能是最差的。综上可知,本文所提的方法不仅输出SINR的收敛速度优于其他方法,同时输出SINR也是最接近最优的SINR的,其性能最佳。
实验4:不同失配角度下的输出SINR
将快拍数固定为1 000次,输入SIR=0 dB,SNR=20 dB。图5为期望信号来波方向的角度失配量从-5°到5°时,不同方法的输出SINR。
从图5可以看出,当期望信号来波方向失配量极大时,本文所提的方法依然与最优的输出SINR接近。而矩阵重构方法只在失配量较小的时候接近最优的输出SINR。 特征子空间投影方法的输出SINR随失配量绝对值的增大而减小。导向矢量校正方法的SINR尽管不随期望信号来波方向角度失配量的变化而变化,但是其输出SINR与最优的SINR有一定距离。Capon和对角加载方法对期望信号来波方向角度失配最敏感,从图5可以看出极小的失配也会造成输出SINR的极大下降,但由于对角加载的加权因子影响,使它略优于Capon方法。综上可知,本文所提方法性能优于其他几种方法。
4 结论
本文提出了联合协方差矩阵重构与导向矢量校正的稳健波束形成方法。该方法利用空间功率谱积分重构干扰加噪声协方差矩阵,排除了采样协方差矩阵中的强期望信号分量,通过空间投影方式校正导向矢量,用校正导向矢量和重构矩阵计算最优加权矢量,进而进行波束形成。仿真实验表明,相较于重构协方差矩阵,校正导向矢量等方法,该方法在强期望信号和期望信号导向矢量失配同时存在时具有更好稳健性,在不同信噪比、不同快拍数、不同失配角度时,输出信干噪比性能接近最优波束形成。
[1]Capon J. High resolution frequency wavenumber spectrum analysis [J]. Proceedings of the IEEE, 1969, 57(8): 1408-1418.
[2]VAN TREES H L. Optimum array processing [M].New York: Wiley, 2002:710-887.
[3]WAX M,ANU Y.Performance analysis of the minimum variance bcamformer [J].IEEE transactions on signal processing, 1996, 44(4):928-937.
[4]Gu Y, Goodman N A, Hong S, et al. Robust adaptive beamforming based on interference covariance matrix sparse reconstruction[J]. Signal Process, 2014, 96: 375-381.
[5]Gu Y J, Leshem A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation [J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3881-3885.
[6]Mu P C, Li D, Yin Q, et al. Robust MVDR beamforming based on covariance matrix reconstruction[J]. Science China (Information Sciences), 2013, 56(4):1-12.
[7]Beck A, Eldar Y C. Doubly constrained robust Capon beamformer with ellipsoidal uncertainty sets [J]. IEEE Transactions on Signal Processing, 2007, 55(2): 753-758.
[8]Feldman D D,Griffiths L J. A projection approach to robust adaptive bamforming [J]. IEEE Trans on Signal Processing, 1994, 42(4):867-876.
[9]Hassanien A, Vorobyov S A, Wong K M. Robust adaptive beamforming using sequential quadratic processing programming: An iterative solution to the mismatch problem [J]. IEEE Signal Letters, 2008, 15: 733-736.
[10]KHAYYAGIYASMFNJ A,VOROYOV S A,HASSANIEN A.Robust adaptive beamforming based on steering vector estimation with as little as possible prior information[J].IEEE transactions on signal processing, 2012,60(6):2971-2987.
[11]Huang L, Zhang J, Xu X, et al. Robust adaptive beamforming with a novel interference plus noise covariance matrix reconstruction method [J]. IEEE Transactions on Signal Processing, 2015, 63(7): 1643-1650.
[12]Zhang W, Wang J, Wu S L. Robust Capon beamforming against large DOA mismatch [J]. Elsevier Signal Processing, 2013, 93 (4): 804-810.
